双馈水轮发电机系统的快速功率响应控制技术

汪健

(国家能源集团江西电力有限公司万安水力发电厂 江西吉安 343800)

为应对化石能源危机和基于环境保护考虑，近年来我国大力发展以水电、光电为代表的清洁能源。根据国家统计局提供数据，2022 年我国水力发电量为1.2×1013kW·h，占全国总发电量的14.3%，仅次于火电。目前，大多数水电站使用的水轮发电机系统均采用同步发电机，以直流励磁控制的方式改变同步发电机的无功功率，这种情况下不仅难以保证水轮机效率最优，而且长此以往还会缩短水轮机的使用寿命。在这一背景下，设计和应用变速恒频的水力发电系统尤为迫切。本文将快速功率响应控制技术应用到双馈水轮发电机系统中，并通过改进控制模式进一步提升了水力发电系统的功率响应及时性和系统运行稳定性。

1 双馈水轮发电机系统转子侧励磁控制技术

1.1 励磁电流控制方式的选择

现阶段双馈水轮发电机系统中常用的“交—直—交”型换流器采用的励磁电流控制方式有两种：一种是基于滞环比较器的电流型控制，另一种则是基于多变量反馈的电压型控制。相比之下，电流型控制可以保证跟踪指令的直接下达和快速传递，更符合水轮发电机系统快速功率响应控制的需求。本文使用单向半桥式逆变电路，以指令电流（iref）与实际输出电流（i*）之间的差值，作为滞环比较器的输入，同时将滞环比较器的环宽（h）设为0.001。

在励磁电流控制中，水轮发电机的转子转速与转差率之间存在线性关系，这里为了提高转速对调控指令响应的及时性和精确性，用转速误差信号代替转差率信号。在控制器方面，使用PI控制器来保证功率调节精度，同时将水轮发电机系统运行中产生的有功功率累计误差，归入有功调节通道，达到误差调节的效果，由此得到了多变量误差反馈控制器[1]。

1.2 快速功率响应控制策略

文章设计的励磁控制器数学模型如下：

式（1）中，iqrref和idrref为转子侧励磁电流q-d轴分量参考值，kpu为控制器的增益值；kp和ki均为有功功率的反馈项系数，Δω与Δp分别为快速功率响应控制策略下转子和定值的转速，两者的计算公式为

式（2）、式（3）中，ωrpu为转子的实时转速，ωrop为给定功率信号对应的最优转速，pref表示功率给定值，ppu为定子侧的有功功率。在励磁控制器数学模型中，kp和ki两项参数是影响有功功率调节速度的主要因素。使用三相静止坐标系分解转子电流指令，得到3 个电流控制指令，分别为ira、irb、irc；将其输入滞环比较控制器中，调制处理后得到开关信号，并用此信号改变主电路开关的闭合状态，最终得到系统运行所需要的转子励磁电流，完成了对水轮发电机系统的变速恒频控制与快速功率响应控制。

1.3 定子磁链观测器的应用

磁链观测模块也是快速功率响应控制策略实现的重要组成部分。由于双馈水轮发电机系统的转子侧励磁控制采用了滞环比较控制与多变量反馈控制联合的矢量控制结构，因此选择合适的定子磁链矢量的相位角尤为重要。磁链观测器就是调节磁链矢量相位角的一种常用工具，现阶段比较常见的磁链观测器有U-I型和U-ω型等[2]。对比来看，U-I型观测器在工作中由于电阻的阻值会受到外部温度变化的影响，进而使得最终测量值无法准确获得，故本文选择了U-ω型观测器，其运作流程如图1所示。

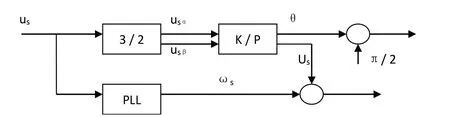
图1 U-ω定子磁链观测器

在U-ω型观测器的应用中，存在以下关系式：

式（4）中，ψs为定子磁链矢量的幅值。假设定子电压（Us）与电网角频率（ωs）维持恒定，那么ψs必然恒定。对定子的三相电压（us）做3/2变换，可以分别得到usα和usβ两个电压分量，利用K/P 模块对所得电压分量做变换处理，得到定子电压相角（θ）与定子电压（Us）。由于定子磁链矢量始终滞后于定子电压矢量π/2 个幅值，因此磁链观测器最终输出的定子磁链矢量相角（θs）还需要减去π/2，即

另外，us经过PLL锁相环处理后，得到电网角频率（ωs），用K/P变换输出的Us与ωs求商，即可得到定子磁链的幅值。

2 双馈水轮发电机系统水轮机侧调节控制技术

2.1 水轮机非线性模型参数的选取

研究水轮机侧调节控制策略时，需要使用到的水轮机非线性模型参数主要有水轮机阻尼常数（D）、水轮机增益（At）以及管道摩擦系数（fp）。本文基于现场实测获得的数据建立水轮机非线性模型，具体方法如下：根据双馈水轮发电机的实际运行工况，确定系统在稳定运行时的输入信号，并根据误差形式构造建立目标函数；获取水轮发电机系统稳定运行时输出的各项数据，如转速、有功功率等，使用智能优化算法处理这些输出数据，根据算法处理结果选出拟合效果最优的一组数据，作为水轮机非线性模型的参数。

2.2 引入多变量综合误差信号的PID控制

本文使用理想电压源模块等效代替无穷大电网，在此基础上设计双馈水轮发电机系统。在忽略低频振荡的前提下，此系统可用于探究水轮发电机并网运行时，不同给定功率下的暂态响应过程，从而帮助我们更加直观地了解系统的动态响应性能，以此来判断快速功率响应控制技术的应用效果[3]。根据双馈水轮发电机调节器的工作原理可知，当给定功率上升时，为了保证能量平衡，需要尽快消解转子惯量，此时必须降低转子的转速。具体实现方式是将水轮机侧转速误差信号减去ΔP值，得到多变量综合误差信号，公式为

式（6）中，ksu为转速误差项系数。如果水轮发电机系统采用PID控制器，则控制器的输出信号（u）可表示为

式（7）中，kp、ki和kd均为PID 控制器的参数。PID控制器的输入和输出流程如图2所示。

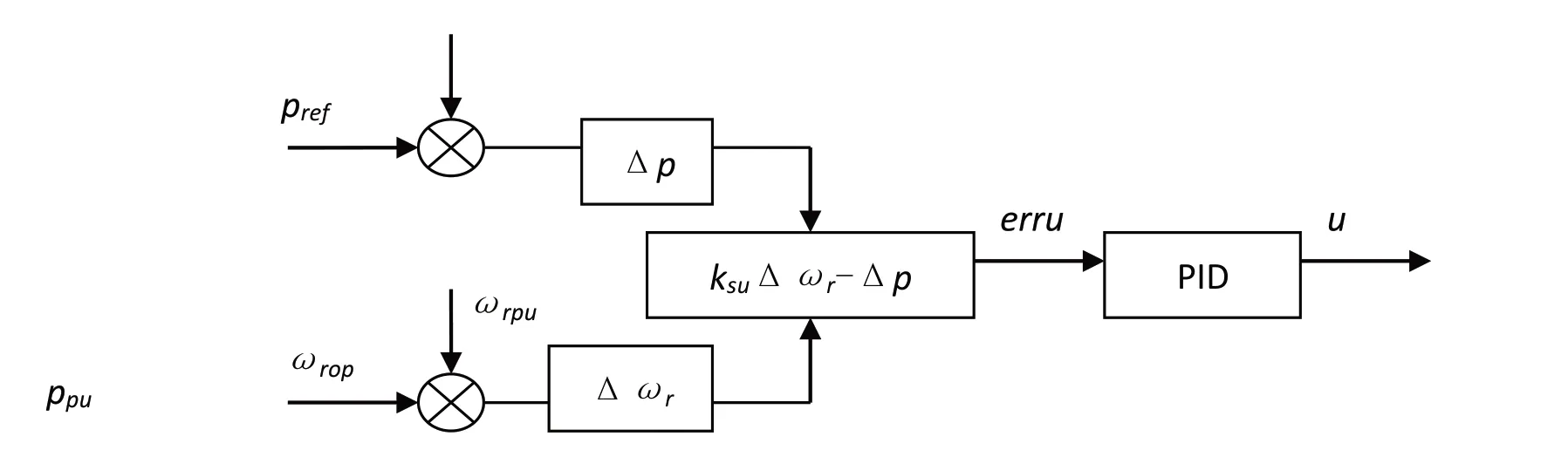
图2 引入多变量综合误差信号的PID控制器

3 双馈水轮发电机系统快速功率响应控制的仿真实验

3.1 仿真设计

3.1.1 模型的参数设定

本文使用电磁暂态仿真软件PSCAD 构建了双馈水轮发电机仿真系统，并对本文提出的快速功率相应控制策略的应用效果展开仿真实验[4]。在此仿真系统中，交流励磁电机模型的参数如下：额定容量（SN）为2 MVA，额定电压（UN）为0.69 kV，额定频率（fN）为50 Hz，转动惯量时间系数（Jpu）为2.85。其中，Jpu可通过电机转动惯量（J）求得，两者的关系式为

式（8）中：ωer为电机额定电角频率；MVAr为电机额定功率；p为电机的磁极对数。水轮机非线性模型的参数如表1所示。

表1 水轮机非线性模型主要参数

按照上述模型参数确定PSCAD仿真系统后，为进一步提高该系统的动态响应品质，还需要进行优化整定。

3.1.2 确定寻优目标函数

使用遗传算法GA 对PID 控制器参数和转速误差项系数做优化整定处理，设定寻优次数为500 次。确定寻优目标函数是优化整定操作的关键步骤，文章基于IAE（绝对误差积分）准则，将寻优目标函数设定如下：

式（9）中：ew为转速差；ep为功率差。在双馈水轮发电机的并网运行中，大多采取功率调节方式。这种情况下要想保证该系统具备良好的功率响应效果，必须要调节寻优目标函数中功率的权重。在本实验中将w1设置为0.7，将w2设置为0.3。

3.1.3 仿真实验内容

为了更加直观地表示本文设计的多变量综合误差信号控制方法的应用效果，设计了对照实验。以传统的“功率主控法”作为对照组，以本文改进的控制方法作为实验组，除了控制方法上有所不同，其他的各项参数以及系统工况均保持不变。

采用改进控制方法的实验组，将有功功率的给定值从原来的1.2 MW 升高到1.5 MW。同时根据寻优目标函数的计算结果，相应的将最优转速从原来的0.90 pu增加到0.95 pu。经过500次寻优整定后，获得5组最优参数。其中有3 组属于PID 控制器参数，分别是：kp=0.93，ki=0.13，kd=0.82。另有两组属于转速误差项系数，分别是ksu=0.81，kpu=0.90。

采用传统功率主控法的对照组，将实验组的多变量误差变成单变量误差，其他处理内容与实验组保持一致[5]。同样经过500次寻优整定后，得到3组最优参数，分别是：kp=1.09，ki=0.18，kd=1.68。

3.2 仿真结果

两种控制方法下双馈水轮发电机仿真系统在不同时间内的有功功率变化情况如图3所示。

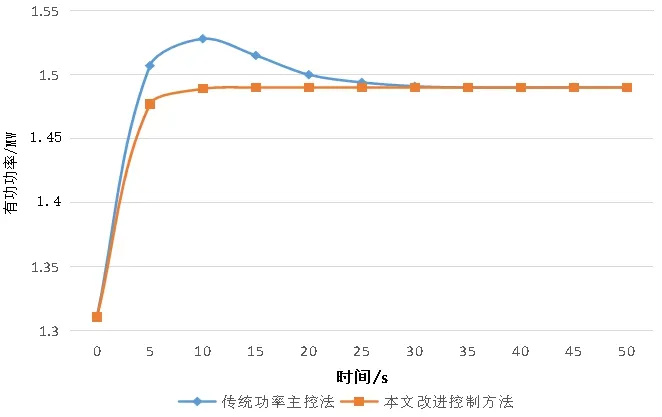
图3 两种控制模式下有功功率随时间的变化曲线

根据图3可知，采用传统功率主控法，此仿真系统的有功功率要想从初始值（1.311 MW）达到稳定值（1.490 MW），需要的调节时间为35 s，超调量为0.038 MW；对比来看，采用改进控制方法，此仿真系统的有功功率仅需要15 s即可达到稳定，调节时间缩短了50%，超调量为0。

两种控制方法下双馈水轮发电机仿真系统在不同时间内的转速变化情况如图4所示。

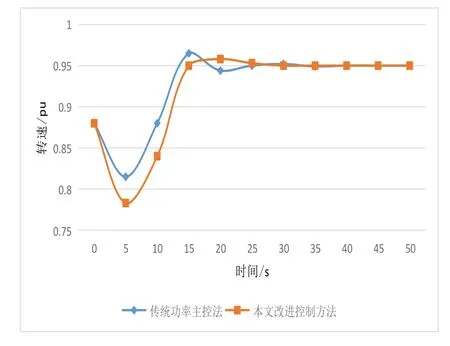
图4 两种控制模式下转速随时间的变化曲线

根据图4可知，采用传统功率主控法，该仿真系统的转速波动变化较为频繁，在整个实验周期内，转速最高值出现在第15 s，为0.965 pu；转速最低值出现在第5 s，为0.813 pu，在40 s 时系统转速达到稳定值。相比之下，采用改进控制方法后，该仿真系统的转速在第30 s 时达到稳定，最低转速为0.783 pu，最高转速为0.958 pu。横向对比可以发现，基于改进控制方法的仿真系统，转速超调量也有所降低[6]。

综上所述，使用本文提出的多变量综合误差信号控制方法建立双馈水轮发电机系统，可以通过水轮机调节子系统和转子侧励磁子系统的联合控制，让系统的有功功率响应更加迅速，并且能够用更短的时间让系统实现变速恒频运行，对进一步提高双馈水轮发电机的运行效果有积极帮助。

4 结语

双馈水轮发电机将水的动能与势能转化为电能时，需要根据机组负荷的变化，灵活、迅速地完成功率响应，才能保证电力系统的可靠和稳定运行，并实现水电转换效率的最大化。以往基于功率主控法的双馈水轮发电机系统虽然也能保持较高的水力效率，但是功率响应存在滞后性，并且超调量较大，不利于系统的稳定运行。本文提出了一种基于转子侧励磁控制与水轮机侧PID控制相结合的策略，从仿真实验结果来看，双馈水轮发电机系统的有功功率响应更加快速，并且超调量更小，在提高水电转化效率的同时还能保证电力系统稳定运行，改良效果显著。