管状曲面上的定倾曲线研究

齐 瑞,秦 路,李政伟

( 1.郑州西亚斯学院 教育学院,河南 郑州 451191;2.郑州市中原区教育局,河南 郑州 450007)

经典的定倾曲线又称螺线,指切向量与固定方向的夹角为常数的曲线。这类曲线有很多重要的性质,如圆柱面上定倾曲线的曲率和挠率之比为常数。文献[1]推广定义了圆环面上的定倾曲线,并得到了这类曲线的具体表达式。管状曲面是一类更广泛的曲面,它可以看成是沿着一条曲线r(u)(称为中心曲线)的各点在法平面以固定半径λ生成的圆周构成的,可以表示为

r(u,θ)=r(u)+λ(cosθβ(u)+sinθγ(u)),λ>0,

(1)

式中:u为曲线r(u)的弧长参数,u∈I;θ为角参数,θ∈[0,2π];β(u)和γ(u)为曲线r(u)的主法向量和次法向量。从管状曲面的研究[2-4]可以看出,圆环面是一种特殊的管状曲面。仿照圆环面上定倾曲线的定义,考虑管状曲面上的定倾曲线。

定义(定倾曲线)对于管状曲面r(u,θ)上的曲线,如果它在每一点处与中心曲线r(u)的夹角为常数,则称为该管状曲面上的定倾曲线。

关于管状曲面上的定倾曲线,本研究得到了以下结论:

主要定理记管状曲面r(u,θ)的中心曲线的曲率和挠率分别为k(u)和τ(u),则与中心曲线夹角为φ的定倾曲线满足下列条件之一:

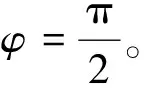
2)r(u,θ(u))=r(u)+λ(cosθ(u)β(u)+sinθ(u)γ(u) ),其中θ(u)满足方程θ′(u)+sinφk(u)cosθ(u)=λ-1(sinφ-τ(u)),或者θ′(u)-sinφk(u)cosθ(u)=-λ-1(sinφ+τ(u))。

推论1若中心曲线挠率τ=±sinφ,则定倾曲线局部为r(u,θ(u)),其中

(2)

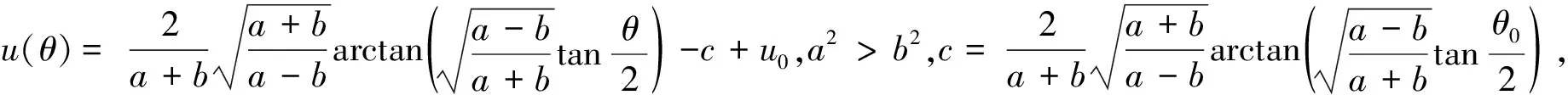
注记1在推论2中,若取τ=0,则可得到圆环面上定倾曲线的解析表达式。

1 主要定理的证明

对于管状曲面r(u,θ)上的截圆r(u0,θ),直接计算得到任一点处的切向量为

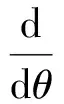
(3)

很明显,该向量落在中心曲线r(u)的法平面,因而与中心曲线的夹角φ=0,这说明r(u0,θ)是定倾曲线。

注意到曲面r(u,θ)上的θ-曲线不是定倾曲线,因此可以假设管状曲面式(1)上的定倾曲线具有形式r(u,θ(u))或者r(u(θ),θ)。

(4)

记中心曲线r(u)的单位切向量为α(u)=r′(u)。利用Frenet标架的运动方程

(5)

(6)

其模长为

(7)

λθ′(u)+τ(u)=±sinφ(1-λk(u)cosθ(u)),

(8)

即有

θ′(u)+sinφk(u)cosθ(u)=λ-1(sinφ-τ(u)),

(9)

或者

θ′(u)-sinφk(u)cosθ(u)=-λ-1(sinφ+τ(u))。

(10)

当夹角φ=0时,方程(8)化为λθ′(u)+τ(u)=0。因此,有

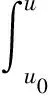
(11)

至此,完成了主要定理的证明。

2 推论1的证明

当τ=sinφ时,方程(9)化为

θ′(u)+sinφk(u)cosθ(u)=0,

(12)

两边积分

(13)

从而得到

(14)

在相差一个参数平移变换下,有

(15)

当τ=-sinφ时,类似方程(10)可得

(16)

这两种情况可给出推论1中的结论。

3 推论2的证明

当中心曲线的曲率和挠率都是常数时,方程(9)和方程(10)可分离变量,积分得

(17)

利用文献[5]中的积分公式

(18)

和

(19)

易得推论2的结论。

4 结语

从管状曲面上定倾曲线的刻画方程来看,要解决一般中心曲线的情形,需要处理复杂的一阶非线性微分方程,而这类方程往往没有解析解,因此要深入研究管状曲面上的定倾曲线,需要从其他角度开展工作,这是后续的研究方向。