基于蝙蝠算法的PID控制参数优化技术与仿真研究
宫 佳
(淮南职业技术学院 机电工程学院,安徽 淮南 232001)
比例-积分-微分(PID)控制器在20世纪30年代出现,因其原理简单、系统模型较为单一,被广泛运用于工业生产中[1]。传统的PID参数整定时产生的误差较大,整定过程比较复杂,并且整定效果较差,产生的震荡和超调量也很大,所以必须优化PID控制参数[2]。PID参数整定主要有以下3个研究方向:对于单输入输出的PID控制系统,存在控制对象变化较大和干扰控制过程变量过多的问题,因此需要继续深化研究PID参数整定的方法;对于多输入输出的PID控制系统,需要研究如何整合各个对象的关系;对于智能PID算法,应将算法与PID参数整定结合,研究出更多智能PID整定方法[3-5]。围绕上述3个研究方向,涌现出很多有效的改进方法。张婧等[6]根据自动控制原理,利用MATLAB软件自带的Rltool工具箱设计了简易的PID控制参数整定方法,实践表明利用该方法调整参数十分方便。林洽怀[7]开发了一种基于PLC的PID控制器,对开环响应进行识别,并在MATLAB/Simulink平台上进行仿真,实验结果表明该方法提高了系统的稳定性。刘延飞等[8]对基本遗传算法的参数进行改进,提出了一种基于改进遗传算法的PID参数整定方法,提升了算法的收敛速度,能防止其陷入局部最优。杨智等[9]针对工业过程中PID参数整定困难的问题,提出了一种个性化惯性权重的粒子群算法,用来优化PID控制参数整定。孙全明等[10]提出了一种基于粒子群优化和LightGBM框架的情景感知多式联运推荐方法,提高了粒子种群的多样性和算法的准确率。蝙蝠算法(bat algorithms,BA)是一种模拟自然界中蝙蝠发射超声波探测周围实体的算法,具有模型简单、参数较少、易于实现的优点[11]。吕磊等[12]建立了一种新的PID控制参数整定方法BA-PID,在PID控制稳定性上优于粒子群算法。基于此,吴晨辉等[13]将BA-PID用于发动机空燃比控制研究中,提高了内燃机瞬态工况下的空燃比。此外,杜学武等[14]发现蝙蝠算法除了对PID控制器有良好的优化效果,还能明显提升模糊PID控制器的控制精度与计算效率。然而,关于蝙蝠算法、粒子群算法与遗传算法的收敛速度、寻优精度和PID参数整定的对比研究却鲜有报道。本研究将蝙蝠算法应用到PID参数整定中,利用蝙蝠算法准确率高、易于实现和结构简单等优点来实现PID控制参数的优化,以达到提高控制系统精度、稳定性和整定速度的目的。
1 相关方法理论概述
1.1 经典PID控制
经典PID控制器一般由比例(P)、积分(I)、微分(D)3个部分组成。PID控制系统如图1所示。
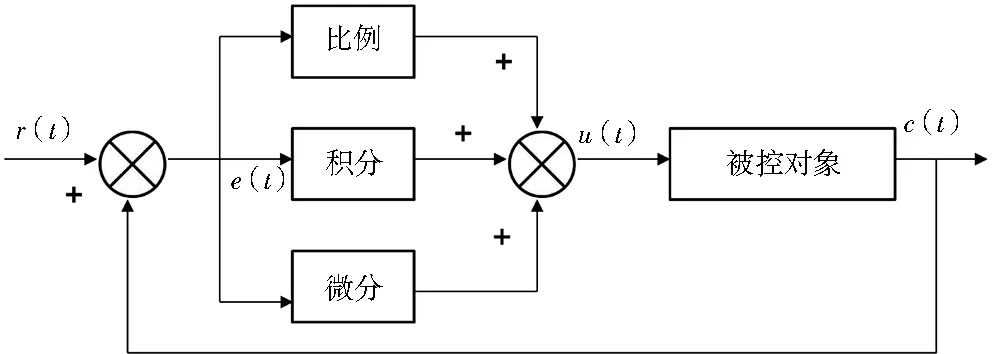
图1 PID控制系统Fig.1 PID control system
PID控制器输入e(t)与输出u(t)的关系一般为
(1)
式中:Kp为比例系数;Ti为积分时间常量;Td为微分时间常量。
1.2 基于蝙蝠算法的PID控制参数优化算法
1.2.1基本原理
图2给出了基于蝙蝠算法的PID控制原理,该控制系统由模拟PID控制器、蝙蝠算法和被控对象组成,其中r(t)是给定输入值,y(t)是实际输出值,e(t)是误差。
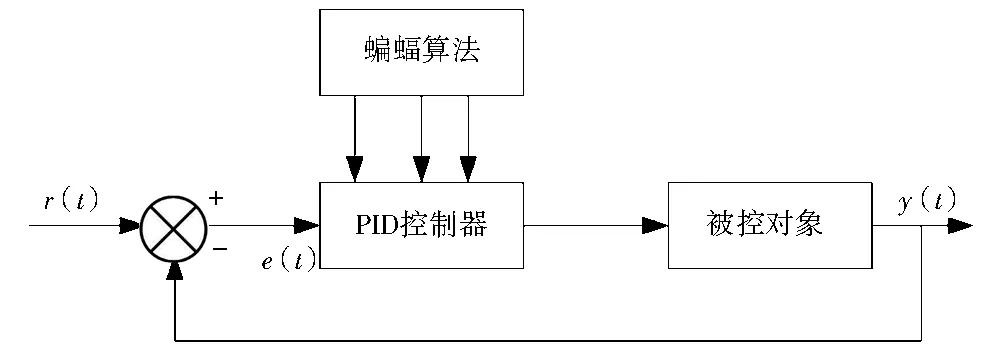
图2 基于蝙蝠算法的PID控制原理Fig.2 The principle of PID control based on bat algorithm
1.2.2蝙蝠算法实现步骤
蝙蝠算法是以种群为整体的群智能算法。蝙蝠算法包括4个步骤:首先初始化蝙蝠算法的参数,然后调整蝙蝠的声波频率,计算当前蝙蝠的适应度,接下来判断随机数r与脉冲发射频度ri的关系,最后计算新解的适应度值f(xnew)并输出全局最优位置。
1.2.3基于蝙蝠算法的PID控制参数优化算法流程
基于蝙蝠算法的PID控制参数优化算法流程如图3所示。初始化蝙蝠种群xi和vi、频率fi、发射率ri及响度Ai。如果未达到最大迭代次数则调整频率,产生新的解并更新速度和位置;如果r>ri,则产生一个局部解;如果通过随机飞行产生了新的解则结束运行;如果r>ri,则接受该新解,增大ri,减少Ai;对蝙蝠进行排序,找到当前最优解x*,结束运行。
2 结果分析与优化
2.1 不同算法仿真结果分析
为证明蝙蝠算法寻优效果更佳,对遗传算法(GA)、粒子群算法(PSA)和蝙蝠算法(BA)进行Griewank和Rosenbrock迭代函数测试,仿真结果见图4。
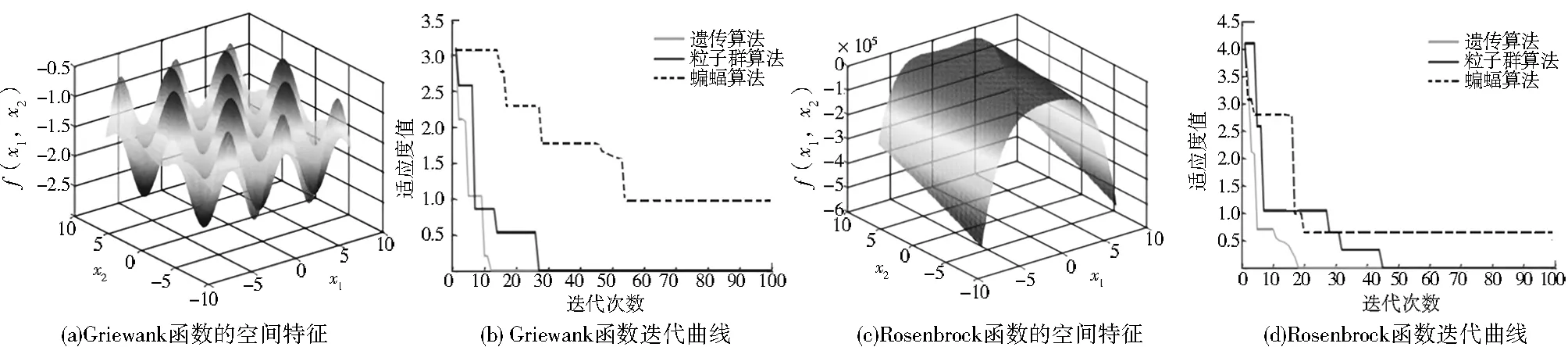
图4 测试函数的仿真结果Fig.4 Simulation results of test function
GA参数设置:交叉概率P=0.75,变异概率Pm=0.15。PSA参数设置:认知系数C1=1.496 2,社会系数C2=1.496 2,惯性权重Wmax=0.9,Wmin=0.4。BA参数设置:蝙蝠数量N=30,频率fmin=-1,fmax=1,A=0.25,r0=0.75,r=0.05,a=0.95。这3种算法的空间维数分别取10、20、50、80,它们的迭代次数都是100。
Griewank函数的空间特征图如图4(a)所示,可以很直观地看出该函数为多峰极函数,由于有许多多峰局部极值点,所以全局最优值不易被找到。3种算法的Griewank函数迭代曲线如图4(b)所示。Rosenbrock函数的空间特征如图4(c)所示,可以看出该函数为单模函数,由于其全局最优值周围比较平坦,所以全局最优值也很难搜寻。3种算法的Rosenbrock函数对比迭代曲线如图4(d)所示。对比图4(b)和(d)发现:粒子群算法和蝙蝠算法的搜索精度与收敛速度均优于遗传算法;粒子群算法虽然最终能找到全局最优值,但在搜索精度和收敛速度上不如蝙蝠算法;在上述2个函数中,蝙蝠算法随着迭代次数的增加,其适应度下降速度最快,并且在迭代初期性能就是最好的,寻优成功率也高于遗传算法和粒子群算法。由此可见,蝙蝠算法的搜索精度和收敛速度都很好。对3种算法分别用函数f1(x)和f2(x)进行20次测试,结果如表1所示。

表1 蝙蝠算法、遗传算法、粒子群算法性能测试比较结果Tab.1 Comparison results of BA, GA and PSA performance tests
由表1可以看出,在最优值、最差值、平均值及标准差方面,蝙蝠算法都是最小的,由此可见蝙蝠算法优于遗传算法和粒子群算法。而且,蝙蝠算法的寻优精度平均值提升很大,说明蝙蝠算法防止陷入局部最优的能力更强,能使种群更加稳定并达到更好的收敛速度和寻优精度。
2.2 基于蝙蝠算法的PID控制参数优化
为验证蝙蝠算法优化PID控制参数的优越性,分别使用蝙蝠算法、增量式PID控制算法和粒子群算法对PID进行参数整定,并对整定结果进行对比。实验中,设置蝙蝠算法和粒子群算法具有相同的寻优空间,寻优空间均为Kp∈[0.01,10],Ki∈[0.01,10],Kd∈[0,10]。选取蝙蝠算法的蝙蝠种群为50只,迭代次数为100,初始响度A=0.5,初始脉冲速率r=0.5,频率f∈[0,2],采样周期为0.001 s,调节时间ts=1 s。选取粒子群算法的粒子数为50,迭代次数为100,认知系数c1=2,社会系数c2=2,惯性权重w∈[0.8,3]。前期实验发现,当蝙蝠数量为50、迭代次数为100、初始响度为0.8、脉冲速率为2时,优化效果最好,因此选择这4个参数值较为理想。
将蝙蝠算法、粒子群算法和增量式PID控制算法优化PID控制参数的结果进行比较,控制输出曲线与误差曲线如图5所示。
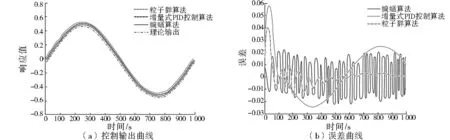
图5 不同算法的控制输出曲线与误差曲线Fig.5 Control output curve and error curve of different algorithms
从图5(a)可以看出,蝙蝠算法优化PID控制参数的实际输出曲线最贴近理论输出曲线,而增量式PID控制算法的实际输出曲线与理论输出曲线偏离较大,优化效果较差,粒子群算法优化PID控制参数的实际输出曲线在理论输出曲线周围震荡很明显,优化效果也比较差。从图5(b)可以看出,蝙蝠算法的误差曲线虽然刚开始震荡明显,但逐渐趋于0,并近似为一条直线,而增量式PID控制算法的误差曲线偏差一直较大,粒子群算法的误差曲线始终在-0.02~0.02震荡,并且震荡很频繁,说明误差较大。
综上所述,蝙蝠算法优化PID参数效果最好,而且很稳定,而粒子群和增量式PID控制算法优化后的实际输出结果和理论输出值偏差较大,稳定性远不如蝙蝠算法。
3 结语
在经典的PID控制中,PID整定过程比较复杂,并且控制效果不佳。本研究将蝙蝠算法应用到PID参数整定中,以实现最优整定。用MATLAB软件进行仿真和分析发现,蝙蝠算法获得的PID参数总体上优于增量式PID控制算法和粒子群算法,误差较小,优化效果明显。然而,由于蝙蝠算法在搜索时陷入局部最优的次数较少,且全局搜索最优的精度较高,导致算法的收敛速度和运行效率大大降低,后续将从数学理论角度出发,使蝙蝠算法在收敛速度和收敛精度上均达到最理想的结果。

