基于图像的三维重建典型技术综述

孙海迅，罗健欣，张艳艳，郑义桀，潘志松

（中国人民解放军陆军工程大学 指挥控制工程学院，江苏 南京 210001）

0 引言

三维重建是指在计算机中建立现实物体或场景三维模型的关键技术。随着计算机视觉的发展，三维重建在医学影像判读、文物修复、自动驾驶、虚拟现实等领域有着广泛应用。按照重建方法，可将其分为传统方法和深度学习方法两大类。传统方法主要是对于在不同视角获取的物体照片，利用相关算法，恢复其三维结构。深度学习方法是通过训练神经网络预测物体的三维模型［1］。深度学习方法对算力要求较高，而传统基于图像的三维重建价格低廉且算法相对成熟，因而应用更加广泛。

基于图像的三维重建主要包括以下流程：图像特征点检测与匹配、稀疏点云重建、稠密点云重建、三维表面重建、表面纹理贴图。本文针对以上流程中的关键环节，选取几种代表性方法进行综述。

1 特征点检测与匹配

特征点是图像中亮度变化剧烈的点或图像边缘曲线上曲率的极大值点，它同周围的邻近点有着明显差异［2］，目前已有多种特征点检测方法［3］。在三维重建过程中，可以通过对不同视角下图像特征点的检测与匹配，求解相机姿态，进而获取三维点云。本文重点介绍两种经典方法——Harris角点检测［4］和SIFT 特征点检测［5］。

1.1 Harris角点检测

角点指图像上两个方向上边缘线的接合点。在一幅图像上取一小块特征区域，如果区域的灰度沿各方向都有较大变化，则认为窗口内存在角点。

设（x，y）为图像上某处像素坐标，I（x，y）代表该点处对应的光度，（u，v）代表位移，I（x+u，y+v）代表位移后的光度，w（x，y）代表权重函数，本文选择高斯函数，则可用E（u，v）度量特征区域位移后与位移前的光度差异，以此判断区域内是否包含角点。

其中，对I(x+u，y+v)进行一阶泰勒展开，即：

其中，Ix、Iy表示图像在(x，y)坐标点处的亮度分别对x、y的偏导数，因而可将上式重写为：

通过对M矩阵的特征值进行分析即可判断Ω 区域是否包含角点，当M的两个特征值λ1、λ2都比较大时，则认为Ω 区域包含角点。同时，文献［4］给出了如下判别方法，当R大于某阈值，认为Ω 区域存在角点。

1.2 SIFT特征点检测

文献［5］提出了一种对旋转、缩放、明暗保持不变的特征点检测方法，通过高斯差分算子（Difference of Gaussian，简称DOG 算子）寻找特征点。高斯空间与高斯差分空间如图1所示。

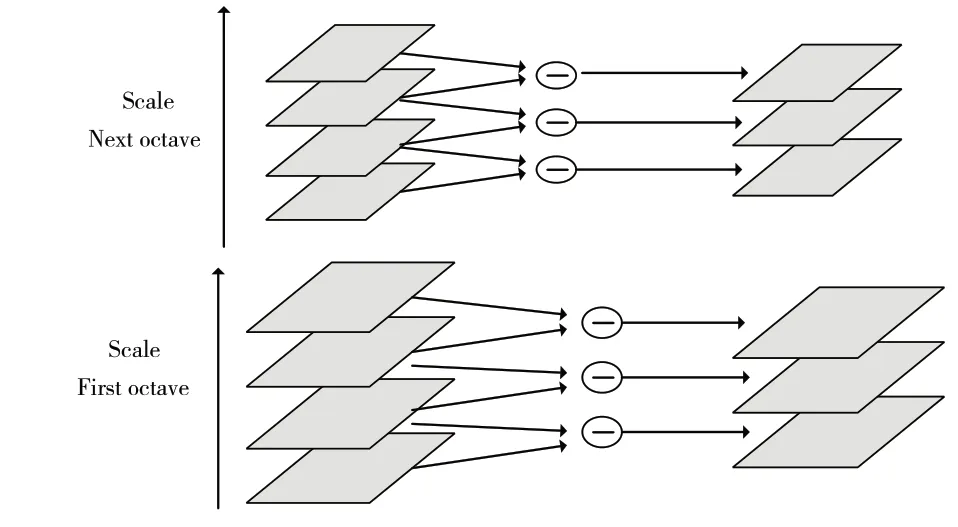
Fig.1 Gaussian space and Gaussian difference space图1 高斯空间与高斯差分空间

首先对原始图像进行降采样形成不同的组（octave），在每组内对图像用不同的高斯核函数（标准差分别为σ、kσ、k2σ......）做卷积形成多张图像。计算方法为：

其中，I(x，y)表示原图像，G(x，y，σ)表示标准差为σ的核函数，L(x，y，σ)表示卷积之后生成的一幅高斯图像，以此构建高斯图像空间（Gussian Space）。

同一组内相邻两幅图像相减得到高斯差分图像空间（DoG Space），计算方法为：

D(x，y，σ)表示生成的一幅高斯差分图像，并且每一组内有效差分数S与高斯图像空间的层数N满足如下关系：

在高斯差分图像空间求极值得到图像特征点，即对每个点与它所在图像与上下相邻两层图像周围26 个像素点的亮度进行比较，如果大于或者小于这26 个点，则作为极值点。

进一步地，通过在亚像素位置上寻找极值点的更精确位置能够从本质上改善特征点的匹配稳定性［5］，图像极值点如图2 所示。于是，在x0=(x0，y0，σ0)T处对函数D(x，y，σ)进行泰勒展开得：

Fig.2 Extremum point of the image图2 图像极值点

令δx=x-x0，将D(x)对其求偏导使之为0，得：

于是精确的极值位置为x=x0+δx，对应的函数值：

其中，偏导数矩阵∇DT(x0)、∇2D(x0)是用像素点附近点的差分形式近似表示［5］。

此外，类似于Harris 角点检测的方法，对图像平面上x处的二阶Hessian 矩阵的特征值施加一定约束，能剔除某些只在一个方向上与其他点有明显差异的点，使得检测到的特征点更加稳定。约束条件为：

图像的主方向通过统计梯度直方图的方法确定，将图像的x轴旋转到主方向上，算法才具有旋转不变性。

SIFT 特征描述子（128 维）同样是统计局部区域梯度信息而生成，通过最近邻搜索方式进行匹配，并将最近邻与次近邻的距离之比限定在较小范围内，以此得到较为精确的匹配对。

SIFT 特征点检测比Harris 角点检测更鲁棒，对旋转、尺度缩放、亮度变化能保持不变，但实时性不高、运算速度较慢，因而出现了诸如SURF［6-7］等方法的改进。

2 稀疏点云重建

稀疏点云重建是根据图像上特征点的匹配关系，通过运动恢复结构（SFM）生成稀疏点云的方法。运动恢复结构是指通过图像间的对应关系，重构相机外部参数（位置和姿态）和内部参数（焦距和径向畸变）。在实现SFM 的过程中，通常包含三角测量，以此求解三维点坐标，得到稀疏点云。

2.1 基本概念

2.1.1 针孔相机模型

针孔相机模型的坐标系包括：世界坐标系、相机坐标系、归一化像平面坐标系和物理像平面坐标系。世界坐标系是物体所在现实世界的坐标系，实际计算时常用相机的初始位置建立世界坐标系；相机坐标系是在以相机中心为坐标原点建立的坐标系，其Z轴通常指向要拍摄的物体。世界坐标系到相机坐标系的坐标变换如图3 所示，相机坐标系下的坐标变换如图4所示。

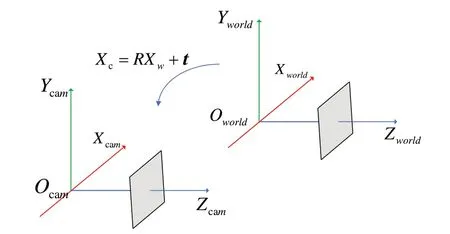
Fig.3 Coordinate transformation from world coordinate system to camera coordinate system图3 世界坐标系到相机坐标系的坐标变换

Fig.4 Coordinate transformation in camera coordinate system图4 相机坐标系下的坐标变换

设世界坐标系下某一点Xw（xw，yw，zw），在相机坐标系下坐标为Xc（xc，yc，zc），二者可通过旋转平移变换得到，于是满足以下关系：

写成齐次形式：

归一化像平面是人为设置的虚拟平面，将其z坐标（距离相机光心距离）设为1。设点Xc的归一化坐标为（x，y），则：

物理像平面平行于归一化平面，指相机CCD 阵列所在的平面。物理像平面坐标也即图像的像素坐标，归一化坐标乘上焦距f和分辨率α（可以合并写为fα），再进行坐标平移后（因为物理像坐标通常以图像左上方为原点）即可得到物理像平面坐标。

因此，从空间点的世界坐标Xw到图像坐标的变换关系为：

其中，K为内参矩阵，［R t］为外参矩阵。

2.1.2 径向畸变矫正

相机的针孔模型与真实的相机成像不尽相同，真实的相机会由于透镜形状引起图像畸变——径向畸变。因此，要从二维图像中准确提取度量信息，必须进行摄像机标定。Zhang［8］提出一种利用棋盘格标定相机的方法，标定过程仅需打印棋盘格，并从不同方向拍摄图片，不仅灵活方便，而且鲁棒性好，如图5所示。

Fig.5 Comparison before and after correction of radial distortion图5 径向畸变矫正前后对比

该方法假设畸变后的归一化坐标与畸变之前坐标存在如下关系：

其中，k1、k2为径向畸变系数，r为坐标点到归一化平面中心点的半径。畸变后的图像坐标为：

在理想情况下：

联立以上等式，可得：

其中，、是通过观察棋盘格上已知的某点在未矫正图像上的位置而得到，u、v是理想情况下利用前面的投影关系计算得到，r是该点到棋盘中心的距离。在棋盘格上选定多点，即可利用最小二乘法解方程得到k1、k2。之后，在矫正后的图像上，即可利用如下关系得到点（u，v）对应的、，并将矫正前坐标（、）处的颜色值作为矫正后图像上（u，v）坐标的颜色值，生成矫正后的图像。

2.2 相机姿态恢复

在对极几何［9］中，常通过图像坐标点的对应关系，求解基本矩阵或单应性矩阵进而求解相机姿态。

2.2.1 通过基本矩阵与本质矩阵求解相机姿态

如图6 所示，X为一空间三维点，O1、O2为两个相机中心，则XO1O2所在的平面称为极平面，π1、π2为两个相机的物理像平面，x1、x2分别为X在两个物理像平面的像素坐标。设、分别为x1、x2对应的归一化平面坐标，[R，t]为O2坐标系相对于O1坐标系的坐标变换矩阵，两个相机的内参矩阵分别为K1、K2，则有如下约束关系：

Fig.6 Diagram of epipolar geometry图6 对极几何示意图

在图像特征点检测与匹配的基础上，利用以上约束关系，即可求得基本矩阵和本质矩阵，进而得到相机的外参数（相机姿态）。文献［10］给出了利用8 对在图像上匹配的特征点计算基本矩阵F的方法，称为8点法。具体为：

设x1=(u1，v1，1)T，x2=(u2，v2，1)T为一对匹配的特征点，根据约束1=0，即：

若令f=(F11，F12，F13，F21，F22，F23，F31，F32，F33)T，则有：

也即每一对匹配点能对F矩阵提供一个约束，而若令F的任一元素归一化（所有元素同时除以某一元素），并不影响1=0 的成立，即F有8 个自由度，因此至少需要8对匹配的特征点即可求得F，当匹配的特征点大于8 时，也可得利用最小二乘法求解。

为增加8 点法的鲁棒性，文献［11］采用了将图像坐标归一化的方法，也称为归一化8 点法。文献［12］提出要对F矩阵增加奇异值约束。文献［13］提出了一种根据奇异值约束对矩阵F进行重构的方法，即在利用8 点法得到F的基础上，将F进行SVD分解：

利用奇异值约束将基本矩阵重构为：F，=Udiag(σ1，σ2，σ3)VT，这样可以使得F-F，的Frobenius 范数最小。

在实际应用中，特征点可能因噪声产生误匹配而使得基本矩阵的估计不准确。为解决这一问题，文献［14］采用随机抽样一致性（RANSAC［15］）方法估计基本矩阵，具体为：

（1）计算采样次数。

其中，z代表期望采样达到的成功率，M代表为达到这一成功率至少需要的采样次数，k代表每次采样求解基本矩阵所需要的点数，p代表所有样本点中内点（匹配准确的特征点）的概率。

（2）对匹配的特征点集中随机采样8 对，利用8 点法估计初始矩阵F。

（3）用Sampson 距离［16］度量点集中所有点，将点划分为内点和外点（误匹配的特征点），并记录当前计算所得F矩阵对应的内点个数。一对特征点的Sampson 距离可表示为：

其中，x1、x2表示不同图像上的一对特征点，F为步骤（2）计算得到的矩阵，下标x、y分别表示某一向量的x分量和y分量。

（4）重复步骤（2）（3）M次，选择内点个数最多的F矩阵和相应的内点。

（5）对所有内点重新执行步骤（2）得到基本矩阵F’。

相机姿态的恢复需要求解本质矩阵。本质矩阵E是一个秩为2 的矩阵，具有5 个自由度，有两个相等的奇异值和一个0 奇异值［17］。与求解基本矩阵F所用的8 点法类似，本质矩阵的求解可以采用5 点法［18］，也可在求得基本矩阵F的基础上，利用以下关系求本质矩阵初始解：

同样地，要对E施加奇异值约束并重构［9］：

在文献［9］中证明，SVD 分解不唯一，如果可以分解为式（30），则也一定可以分解为：E=Udiag(1，1，0)VT。如果可以将本质矩阵进行SVD 分解，则E=[t]×R有如下4 种可能情况：

从图7 可以看出，4 种情况中只有一种情况是空间点X同时位于两个相机的镜头前方，因而只要用一个点做测试，看它是否位于两个相机的前方，即可选择出正确的相机姿态。

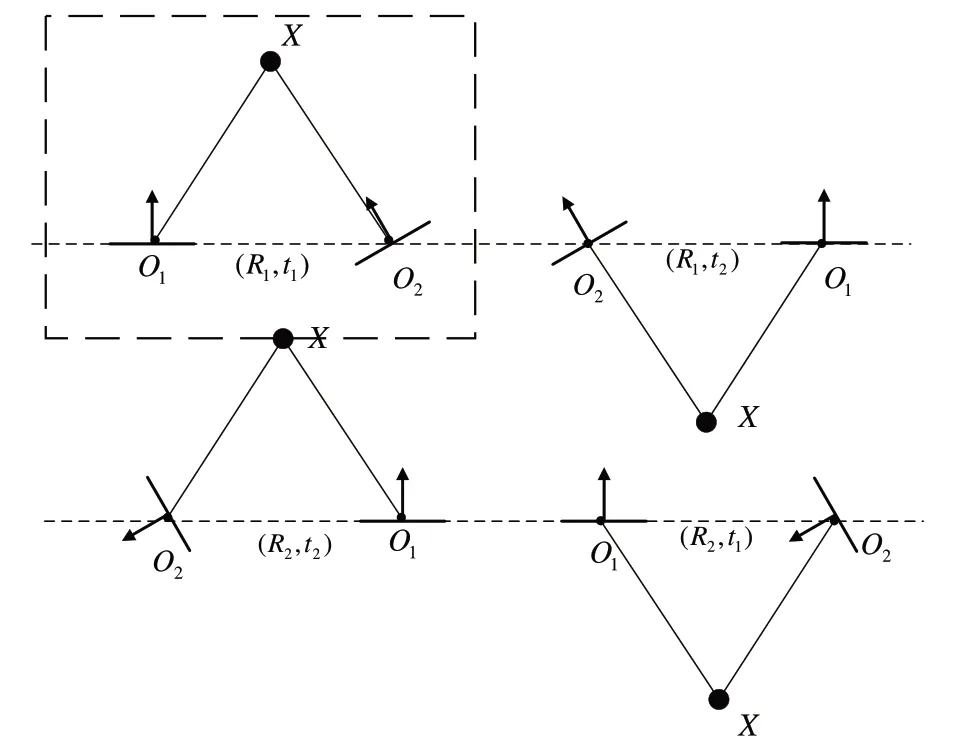
Fig.7 Choice of camera pose图7 相机姿态选择

2.2.2 用单应性矩阵求相机姿态

文献［19］指出，当图像上匹配的特征点均来自于空间中同一个平面时，无论有多少这样的匹配点，它们对基本矩阵F的约束不会多于4 个，这将导致求解基本矩阵F的结果不稳定。此外，当相机姿态只有旋转没有平移时（从O1变换到O2是纯旋转，t=0），E=[t]×R=0，难以通过对E的分解求解R。

如图8 所示，若空间中一平面π 方程为：nTX+d=0，则空间点X 对应的两幅图像上的投影x1、x2有如下关系：

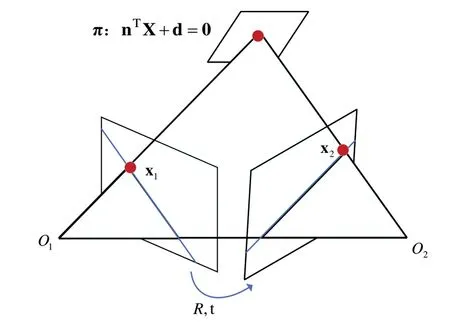
Fig.8 Diagram of homography transformation图8 单应性变换示意图

其中K1、K2分别为两个相机的内参矩阵。若相机为纯旋转变换，即t=0，则H=K2RK1-1。对于H的求解方法，同样可以采用类似于求解基本矩阵F的方法，利用两幅视图上匹配点的约束关系x2=Hx1，H矩阵有8 个自由度，而一对匹配点能提供两个约束，因此至少要4 对匹配点即可求解H［20］。此外，可以采用RANSAC 的方法估计H，然后便可对H进行分解以求解R和t［20］。

2.3 三角测量

在已知相机参数和匹配点的前提下，即可利用三角测量恢复空间点的三维坐标，具体方法如下：

2.3.1 直接线性变换法

文献［9］提出了直接线性变换法。设第i个相机的投影矩阵为：Pi=Ki[Ri，ti]，空间点的三维坐标为X=[x，y，z，1]T，对应在第i个视角的图像坐标为xi=[ui，vi，1]T，di表示X点在第i个视角下的深度，即相机坐标系下的坐标zc。则：

两边同时叉乘xi，得：

其中，第3 个方程与前两个线性相关，则一个观测视角能对X提供两个约束，而X有3个自由度，因此要求解X，至少需要图像上一对匹配点，也即至少要从两个视角对其进行观测。当点数N 大于2 时，还可以构建方程组利用最小二乘法求解：

2.3.2 RANSAC方法

在存在外点的情况下，可以用RANSAC 方法求解［15］。主要步骤如下：①RANSAC 采样次数，设置内点阈值（重投影误差）；②随机采样一对视角，计算空间点三维坐票；③计算每个视角中的重投影误差，统计内点个数；④重复步骤②、③直到满足采样次数，选择内点数最多的视角；⑤利用所有内点重新计算三维点坐标。

此外，在利用相机匹配对进行三角测量计算三维点时，可以从图像中提取EXIF 初始值以获取焦距［21-22］。

2.4 PnP问题

PnP 问题指根据已知的三维点坐标和对应的二维点，求解相机内外参数的问题，这在增量式SFM 中经常被用到［21］。

常用的方法为直接线性变换法，设相机的投影矩阵为：P=K[R，t]，空间点的三维坐标为X=[x，y，z，1]T，对应的图像坐标为x=[u，v，1]T，d表示X点的深度，即相机坐标系下的坐标zc。则：

P矩阵共有12 个参数，而一对3D-2D 对应点能提供2个约束，因此至少需要6 对匹配点即可求解P。因为P[：，1：3]=KR，且K为上三角阵，而R为正交矩阵，可以对P[：，1：3]-1进行QR 分解，即可求得R-1和K-1，进而求得K和R。又P[：，4]=Kt，则t=K-1P[：，4]，得平移向量t。

文献［23］提出一种计算PnP 问题的Kneip 算法，利用三维点构建一个平面作为过渡坐标系，进而求解相机的内外参数。此外，同样可以用RANSAC 方法实现Kneip 算法。求解PnP 问题还有其他几种方法，如用4 对不共面的点进行求解的P3P 方法［24］，利用4 对以上不共面或者3 对共面点进行求解的ePnP 法［25］，以及利用深度学习与传统方法相结合的EPro-PnP 方法［26］，实现端到端的三维位姿预测。

2.5 捆绑调整

由于噪声的影响，以上初步求得相机内外参数和三维点坐标还不够准确，捆绑调整（Bundle Adjustment）［27］可以同时对三维点坐标和相机参数进行非线性优化。捆绑调整如图9所示。

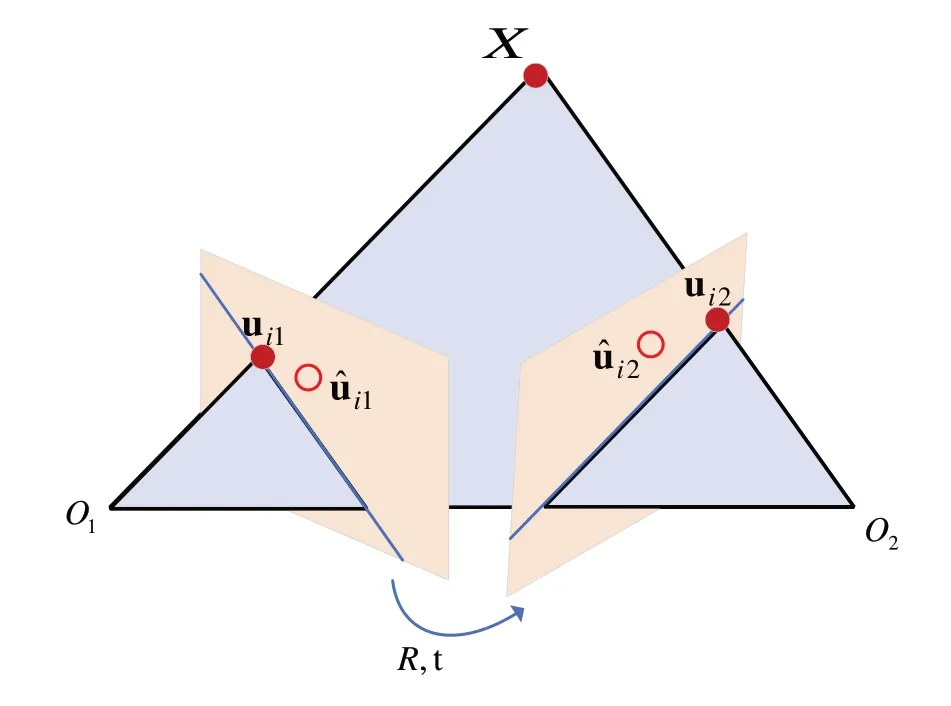
Fig.9 Diagram of bundle adjustment图9 捆绑调整示意图

设χij=1 表示第i个点在第j个相机中可见，χij=0 表示第i个点在第j个相机中不可见；Xi=(xw，yw，zw，)T表示第i个三维点的世界坐标；Pj表示第j个相机的内参以及世界坐标系与第j个相机的外参数；表示第i个点在第j个相机中的观测点；uij表示第i个点在第j个相机中的投影点。

则在有n个三维点和m个视角时，可构建损失函数：

其中，θ=(P1，...Pm，X1，...Xn)为待优化的量。对无约束非线性最小优化问题对于最优化问题g(θ)=通常可用以下几种方法。

2.5.1 最速下降法

假设g(θ)在θt处可微，则它在θt处有泰勒展开（展开到一阶）。

其中，θ=θt+δθ，当(∇g(θt))Tδθ＜0 时可保证g(θ)的值在下降，当δθ取梯度的反方向时，可达到最快下降速度。

算法流程如下：

Step1：给定初始点θ0，迭代终止阈值ε和步长λ，令t=0。

Step2：计算∇g(θt)，若‖ ‖∇g(θt) ≤ε停止迭代，输出θt，否则转下一步。

Step3：取θt+1=θt-λ∇g(θt)，t=t+1，转Step2。

2.5.2 牛顿法

最速下降法是收敛的，但最终的收敛是线性的，而且通常很慢，并且在某些情况下无法找到二阶多项式的最小值，此时可用牛顿法［28］。

假设g(θ)在θt处二阶可微，且假定二阶导数∇2g(θ)总是正定，则以它在θt处二阶近似函数Q(θ)极小值作为下一次迭代点θt+1。同样，将Q(θ)泰勒展开为：

对θ求梯度令其为0，可得：

算法流程如下：

Step1：给定初始点θ0，迭代终止阈值ε和步长λ，令t=0。

Step2：计算∇g(θt)，若‖ ∇g(θt) ‖≤ε，停止迭代，输出θt，否则转下一步。

Step3：取θt+1=θt-λ(∇2g(θt))-1∇g(θt)，t=t+1，转Ste p2。

2.5.3 高斯—牛顿法

牛顿法虽然速度快但计算量大，需要保存二阶Hessian 矩阵的逆矩阵，高斯—牛顿法与牛顿法类似，但区别是它基于f(θ)在θ附近的线性近似［29］，即设p(θ)=f(θ)-x，对其泰勒展开为：

令JT(θt)=∇f(θt)=∇p(θt)，则：

与牛顿法相比，用JT(θt)J(θt)代替∇2g(θt)，降低了运算复杂度。

2.5.4 Levenberg-Marquardt法

最速下降法是用平面在局部拟合损失函数，牛顿法是用二次曲面拟合，当∇2g(θ)在某区域负定时，牛顿法可能收敛到局部极大值，高斯—牛顿法在J(θ)不满秩时可能失效［28］。Levenberg-Marquardt 法［30-31］是将最速下降法和高斯—牛顿法有机结合，使用“信赖阈”控制下降速度的方法。当收敛速度较快时，信赖阈增大，算法趋向于高斯—牛顿法；当收敛速度慢时，信赖阈减小，算法趋向于最速下降法，优点是只用到一阶雅各比矩阵，计算速度快，对初始值有一定的鲁棒性。

通过求解增量正规方程得到δθ。可见，当λ趋向无穷大时，(JT(θt)J(θt))δθ=-∇g(θt)，近似于高斯—牛顿法；当λ趋近于0时，δθ=-∇g(θt)，近似于最速下降法。

Levenberg-Marquardt 法的主要流程为：

Step4：通过求解增量正规方程，得到δθ。

2.6 运动恢复结构分类

典型的运动恢复结构方法有增量式（Incremental SFM）［32-35］、全局式（Global SFM）［36-37］、分层式［38-39］。

2.6.1 增量式运动恢复结构

主要步骤包括：图像特征点检测与匹配、构建图像连接图、初始化、增量式重建新的视角、全局捆绑调整。

（1）图像特征点检测与匹配。采用上文所述方法，SIFT 方法检测的特征点比较稳定，其应用较广泛［33-34］。

（2）图像连接图构建。每一张图像形成图上的一个结点，具有特征匹配点的两幅图像之间有边相连，结点的边越多，表示与其具有匹配的特征点的其他图像越多。从图10 可以看出，白天和夜晚拍摄的图像因为光度差异会在连接图上形成两个簇［33］。

（3）初始化。选择一对初始相机进行Tracks 重建（三角测量）恢复三维点坐标，然后进行Tracks 滤波和捆绑调整以优化估计的三维点坐标和相机内外参数。

其中，初始相机对的选取要遵循一定的原则：匹配点足够多、基线足够长、满足单应性的匹配点尽量少［33-34］。文献［34］指出，由于冗余数据的存在，从图像连接图中的密集位置进行初始化通常会使得重建更加鲁棒和准确。

Tracks 滤波是指滤除Tracks 重建中生成的错误点（包括无穷远处的点和重投影误差过大的点）［21，33］，以降低后续运算复杂度。

（4）新的视角增量式重建。选择能看到已被估计的三维点最多的视角，利用PnP 方法［21］或者RANSAC 方法［33］求解新视角的相机姿态，然后对单个相机姿态进行捆绑调整。下一步对新视角能看到的点进行Tracks 重建和滤波，以此优化三维点的坐标。

（5）全局捆绑调整。对所有已加入的相机内外参数和三维点坐标进行一次全局的非线性优化，由于这一方法运行时间较长，可以在加入多个视角之后运行一次［21］。

增量式运动恢复结构如图11 所示。其主要优点是：对误匹配的特征点鲁棒、场景结构可在调整中不断优化。缺点是：对初始视角的选取和视角添加顺序敏感、大场景下的累计误差会导致场景漂移、捆绑调整重复进行导致效率低。文献［35］提出一种与RANSAC 相结合提升精度的增量式运动恢复结构方法。

Fig.11 Incremental structure from motion图11 增量式运动恢复结构

2.6.2 全局式运动恢复结构

由于捆绑调整比较耗时，全局式运动恢复结构同时估计所有相机的旋转矩阵和平移向量，生成三维点后，只运用一次捆绑调整进行优化。文献［36］提出一种估计全局相机姿态的方法。

首先，在生成图像连接图之后，利用任意两幅图像的特征点匹配关系，计算两个相机的相对旋转矩阵Rij和平移向量tij，通过最小化如下关系求解所有相机相对于世界坐标系的旋转矩阵。

其次，进行全局旋转矩阵滤波，根据求得的Ri与Rj优化图像连接图，即当时，认为相机i与j之间存在错误的连接边，要删除。

最后，利用求得的相机姿态求解三维点并进行一次全局的捆绑调整。

文献［37］提出一种多种信息融合的方法，在求解过程加入了GPS等辅助信息，对结果进行优化。

全局式运动恢复结构如图12 所示。其主要优点是：没有误差积累，误差均匀分布在连接图上；对初始相机选取和相机添加顺序不敏感；捆绑调整仅执行一次，重建效率高。不足之处主要体现在：相机位置求解时对匹配外点敏感，鲁棒性不足；连接图边界被过滤，容易造成部分图像丢失，导致重建不完整。

Fig.12 Global structure from motion图12 全局式运动恢复结构

2.6.3 分层式运动恢复结构

文献［38］提出基于聚类方式的分层式运动恢复结构，如图13 所示。其主要步骤为：利用已知视角创建一个局部模型进行捆绑调整，加入一个新的视角，两个模型融合捆绑调整。这种方法计算效率高，且算法稳定，不依赖初始相机的选取，避免了大场景中的误差积累和漂移，但规则设计较为复杂。

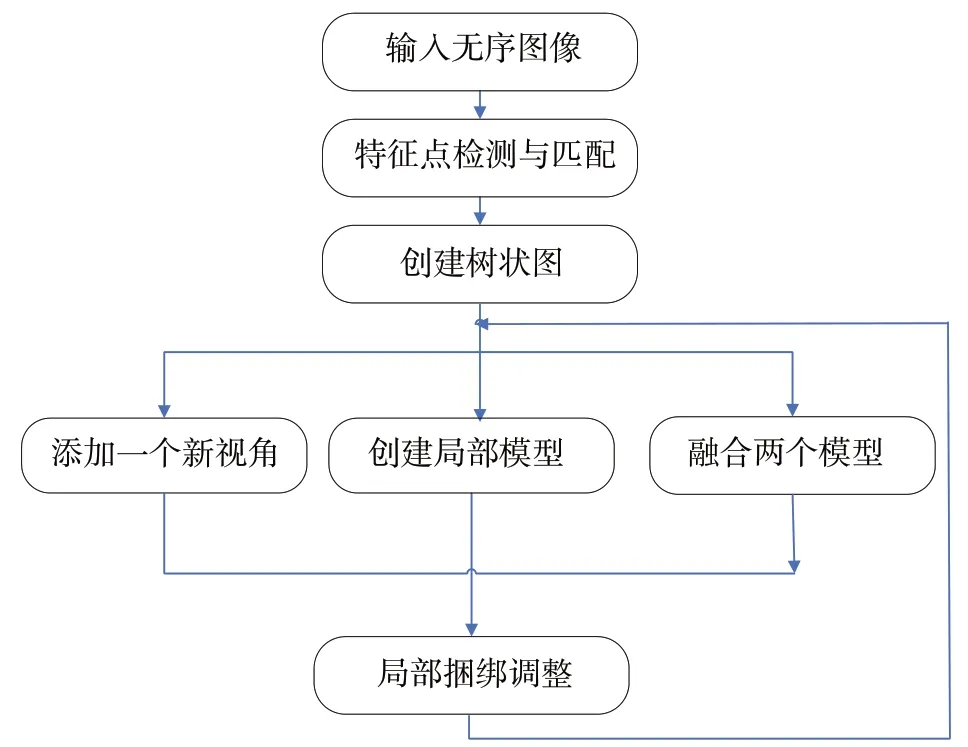
Fig.13 Hierarchical structure from motion图13 分层式运动恢复结构

3 稠密点云重建

基于图像的三维重建中，稠密点云的获取通常基于多视图立体技术（Multi-view Stereo，MVS）。该技术的优点是成本低、精度较高、图像来源广；缺点是计算速度慢。

MVS 中常用的一个基本假设是光度一致性假设（Photo-Consistency），是指同一空间的点在不同视角的投影，光度应该相同，重建的关键是恢复光度一致性的点。光度一致性度量方式有：误差平方和（SSD，Sum of Squared Difference）、归一化交叉协方差（NCC，Normalized Cross Correlation）。具体为：

其中，f和g分别为特征描述子的特征向量、为描述子的均值向量，δf、δg为描述子向量标准差。

基于多视图立体技术（MVS）的稠密点云重建主要有基于体素的方法、基于深度图融合的方法和基于空间patch 扩散的方法。

3.1 基于体素的方法

基于体素的方法是指将空间划分为很多体素，通过图像序列的约束计算体素内三维点的方法。空间划分包括两种类型：一种是规则体素的划分［40］，即将空间划分为小立方体；另一种是不规则体素的划分［41-42］，即将空间划分为小四面体，如图14所示。

Fig.14 Dense reconstruction based on voxels图14 基于体素的稠密重建

这种方法的优点是：生成规则的点云、便于提取物体的平面。其缺点是：精度受到空间划分分辨率的影响，仅适用于小场景，单个物体，遮挡较少的场景，难以处理高精度、大规模的场景。

3.2 基于深度图融合的方法

基于深度图融合的方法［43］是利用SFM 产生的稀疏点云构建种子栅格（patch），通过区域生长对patch 进行优化后生成不同视角下的深度图，再将不同视角深度进行融合的稠密点云重建方法。该方法主要包括以下3 个步骤：数据预处理、区域生长、深度图融合，如图15所示。

Fig.15 Dense reconstruction based on depth map fusion图15 基于深度图融合的稠密重建

3.2.1 数据预处理

patch 是以空间中的3D 点中心建立一个很小的栅格，栅格的分辨率与图像分辨率以及3D 点的位置相关。patch的中心点即为3D 点的位置，patch 的朝向即为3D 点的法向量，patch 上的每个点可以投影到不同视角中计算NCC 用于度量光度一致性。

其预处理包括：通过SFM 重建的稀疏点构建种子patch、构建不同分辨率的图像以处理图像分辨率不同情况、全局视角选择。全局视角选择是指选择满足特定条件的视角用于区域生长。一般要满足以下条件：①图像具有相同的内容，外观——通过共享sift 特征点的个数；②图像具有足够大的视差（宽基线）——通过视线的夹角；③图像具有相似的分辨率——通过计算投影球半径。

为使得计算加速，在生成某一视角的深度图时，文献［43］从以上全局视角中选择4 个视角，称为局部视角。局部视角的选择要求：NCC值大于一定的阈值，并且和已经选择的视角的极平面要足够分散（不共面），如图16所示。

Fig.16 Diagram of view selection图16 视角选择示意图

3.2.2 区域生长

在建立初始种子patch 后，可以利用种子patch 逐步扩张的方法在其邻域生成新的patch。其主要步骤包括：①对稀疏点云中的种子patch 以置信度（光度一致性）建立优先级队列；②估计初始稀疏种子点的深度；③对每个种子点进行非线性深度优化；④每次优化完后，如果图像上的对应像素没有深度值或当前像素的置信度值高于邻域像素一定范围，则将其像素添加到队列中。

其中，非线性优化的数学模型为：

其中，i、j是patch 中的采样点，k为视角个数。IR(i，j)表示点在参考图像上的光度，ck是颜色尺度，由于IK(i，j)表达式中含有深度信息，因而可以利用梯度下降等优化方法对E 进行优化，进而求解像素点深度。优化求解结果如图17所示［43］。

Fig.17 Reconstruction effect based on depth map fusion图17 基于深度图融合的重建效果

3.2.3 深度图融合

深度融合是指在三维空间合并位置相近的点。融合过程同样要对点施加一定的约束，通常包括一致性约束、可视性约束。一致性约束是指相同的点在不同视角下的深度应当具有一致性；可视性约束是指在图像上可视的三维点在融合后的深度图上不能被遮挡。如图18 所示，A 和C 将被认为是错误的点，予以剔除，B 将被选择为正确的点。

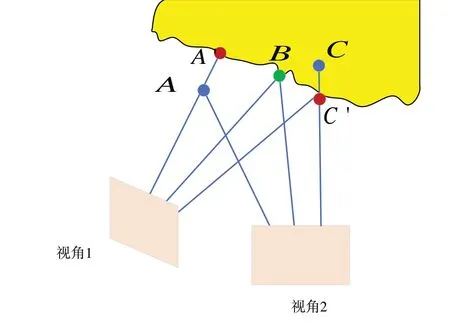
Fig.18 Diagram of consistent point selection图18 一致点选择示意图

深度图融合方法的特点为：邻域视角选择提升了深度估计的准确度，对一些有遮挡、障碍物较多的场景能较好地进行处理，适用场景广泛，只用到光度一致性约束和可视性约束，算法实现简单。

3.3 基于空间patch扩散的方法

与深度图中在二维图像上进行patch 扩张不同的是，基于空间patch 扩散的方法［44］采用的是在空间中对三维patch（大小为5x5 共25 个三维点）进行扩散，最终使patch覆盖物体表面。

重建流程如图19所示。

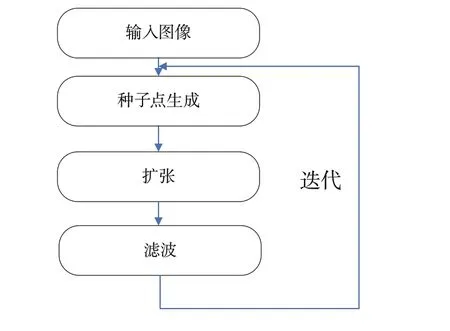
Fig.19 Reconstruction process based on patch diffusion图19 基于空间patch扩散重建流程

初始种子点生成采用SIFT 等特征点；扩张过程对已重建三维点的邻域进行匹配，滤波过程采用两种约束去除噪声点：光度一致性约束和可视性约束。

初始3D patch 的生成步骤：①在图像上均匀计算SIFT/Harris 特征；②沿极线进行搜索找到匹配特征点；③对匹配对，通过三角化建立patch，法向量指向参考图像，通过光度一致性约束对可视图像进行筛选；④对patch 位置和法向量进行优化。

空间patch 扩散步骤为：①将三维patch 投影到图像上；②如果相邻cell 没有patch 且深度连续，则进行patch 扩散，新建patch 的法向量初始值等于领域patch，新建patch的位置设置为当前cell 的视线和邻域patch 所在平面的交点；③计算初始patch 的可视图像，并进行优化。

扩张过程中并没有考虑到可视性的情况，滤波过程的主要目的是利用各种约束对这些不合理的点进行筛选。可用的约束包括可视性约束，可视图像个数小于一定阈值，图像邻域中的cell同时也是空间邻域，其比例小于一定阈值（0.25）。对于每一个patch，统计它所在及相邻image cell 中的所有patch。如果3D 空间中与相邻的patch 比例小于一定值（0.25），则认为是孤立点，将被移除。

PMVS 和基于深度图的重建方法类似，基本原理也是基于光度一致性，并且采用区域生长的方式进行稠密重建，同样适用于杂乱有遮挡的大规模场景。算法优点是：适用性强，适用于各种形状的物体，能够直接重建出完整的稠密点云，不需要进行单独的深度图融合；重建过程中同时考虑了可视性约束，能够得到更加准确的重建结果。其缺点是不适用于非朗伯面（Non-Lambertian），并容易产生空洞，计算量非常大。

近年来，也有针对以上算法不足的改进方法，如：文献［35］利用并行计算提升点云重建速度；文献［45］针对在小范围场景三维重建过程中存在离群点的现象，将PMVS 算法与统计分析法相融合提出一种改进的点云滤波算法，提高了重建精度。

当前，稠密点云重建面临的主要问题与挑战是：①弱纹理和朗伯面——不能满足光度一致性约束；通常需要先验形状约束进行重建；②细长结构重建——很难得到像素级别精度的深度值；通常的解决方法需要进行语义级别的重建；③动态场景重建——图像序列的重建方式可以捕捉动态场景，但是基本只适合于实验室环境；动态物体的重建需要结合形状先验、高级语义信息等。

4 三维表面重建

在得到稠密点云后，利用各种算法可以从点云重建物体表面。三维物体的表面表达方式包括：边界表示法、空间划分法、构造体素法。边界表示法用四边形、三角形、参数曲面或者非参数的曲面表示物体形状，具有稳定性强、灵活性强、有助于表示表面细节。空间划分法将物体内部划分成细小连续实体以描述物体形状。构造体素法通过集合运算（并、交、差）将简单形状组合成复杂形状，只能用来表示较为简单的实体，无法用于形状复杂或表面精细的物体。

计算机视觉中最常用的三维模型表示方式为三角网格（Triangular Mesh）。其基本结构包括：顶点（Vertex）、面片（Facet）、边（Edge）。点、线和面上的各种属性包括：颜色、法向量、纹理坐标（Texture Coordinate）。

常用的三维表面重建方法有：基于二元分割的表面重建方法、基于符号距离场的表面重建方法。

4.1 基于二元分割的表面重建方法

其主要思想是将空间划分成一组小单元（体素/四面体），采用二元分割思想将这些小单元划分成内部和外部两类，介于内部和外部之间的面即为物体表面，如图20所示［43］。

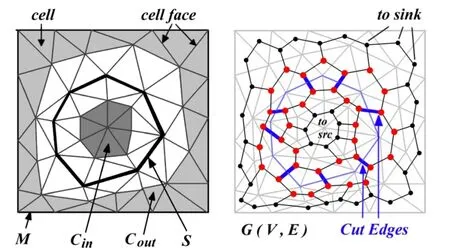
Fig.20 Surface reconstruction based on binary segmentation图20 基于二元分割的表面重建

在稠密点云的基础上进行表面重建主要经历的步骤如下：

4.1.1 德劳内三角剖分

德劳内三角剖分（Delaunay Triangulation）是指将点云中的相邻点用一种特定的方式连线，使得任意相邻的4 个点构成空间中的一个四面体。德劳内三角剖分具有以下特性：

（1）空球特性。任意4 个点的外接球内都不含有其他点。

（2）最大化最小角。德劳内三角剖分最大化四面体上三角形的最小角。

（3）对偶性。德劳内三角剖分和维诺图（Voronoi Diagram）是互为对偶的关系，如图21所示［43］。

Fig.21 Duality of Delaunay triangulation and Voronoi diagram图21 德劳内三角剖分与维诺图的对偶关系

文献［46］给出了一种增量式进行德劳内三角剖分的方法。

三维表面的生成问题将转化为四面体的二元标记问题，即将一剖分四面体标记为“外部”，另一剖分四面体标记为“内部”，内外交界处的空间曲面即为物体表面。

4.1.2 用图分割方法提取物体表面

图分割（Graph Cut）是指对一特殊的有向加权图的某些边进行切分，将图分割为没有交集的两个部分，使得边的权重损失最小［46-48］。这一图的特殊之处在于包含两个特殊的节点：源节点和汇节点，其中源节点只有出边，而汇节点只有入边，如图22 所示，边的粗细表示权重大小，切分目标是选取权重最小的边切分。

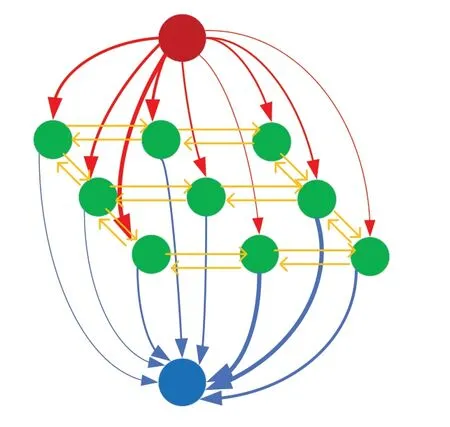
Fig.22 Diagram of graph cut图22 图分割示意图

在对稠密点云进行德劳内三角剖分后，根据其与维诺图的对偶关系生成维诺图：即使四面体的中心作为维诺图各小区域的中心，四面体的三角形表面作为维诺图的边。在一定约束条件下，对维诺图的边赋予一定权重并将其看作有向加权图，于是便可进行图分割提取物体表面，如图23所示［43］。

Fig.23 Surface reconstruction based on graph cut图23 基于图分割的表面重建

对维诺图的边赋予权重的方法包括以下几种：可见性约束、光度一致性约束、平滑性约束［46］、剪影约束［43］、表面质量约束［47］。

重建结果如图23所示［43］。

4.1.3 网格细节优化

用二元分割方法提取的物体表面，由于点云存在噪声或者空洞，会导致原始网格存在噪声或者空洞，无法捕捉场景细节，因而需要对网格细节进行优化（Mesh Refinement）。

文献［44］提出一种基于光度一致性的网格细节优化方法，即利用多视角图像再次计算相同点在不同视角下的重投影误差，通过同时或者逐个移动网格顶点的位置，使重投影误差最小，也使光度一致性最好。度量光度一致性的能量函数为：

其中，h(Ii，)(x)表示图像i和j之间在像素x处与光度一致性呈单调递减的某一函数；表示将图像i通过曲面S重投影到图像i上；表示重投影的有效区域；Eerror(S)的含义即为所有两两视角对下相同区域的重投影误差之和；Eerror(S)越小，说明生成的网格越准确。

要优化网格顶点位置，即要求以上能量函数关于网格顶点的梯度，应利用梯度下降法进行优化。但由于网格顶点的位置变化实际上会影响其周围三角面片上点的位置，于是先计算关于某顶点周围三角面片点的梯度，再采用插值方法计算这一顶点的梯度，插值方法采用重心坐标法。Eerror（S）对［Xi］的梯度为其对网格上Xi一周所有点梯度的加权和具体如图24所示。

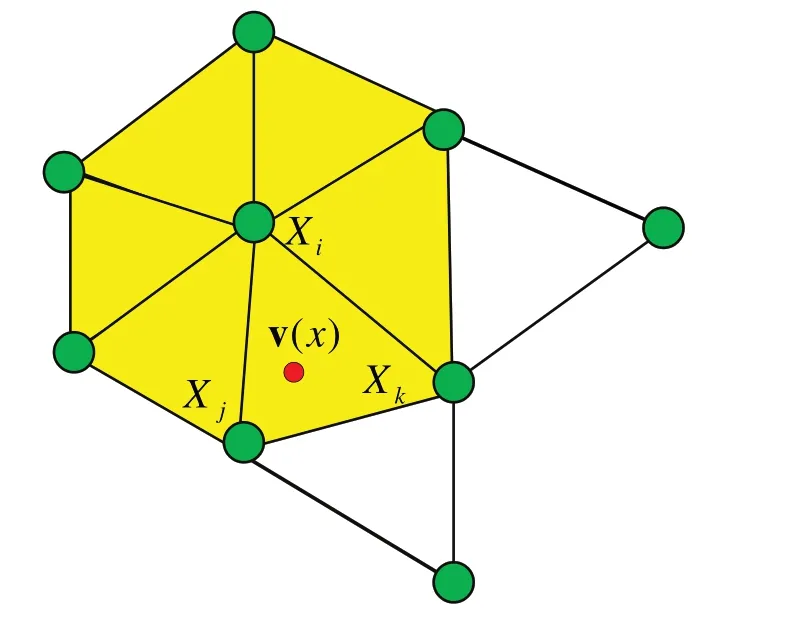
Fig.24 Grid vertex position optimization图24 网格顶点位置优化

其中，v(x)表示顶点Xi一周三角网格上的任意一点，φi(x)表示v(x)相对于Xi的重点坐标，∇E是Eerror(S)相对于v(x)的梯度。

基于二元分割的表面重建方法具有以下特点：①算法流程简单，容易实现；②适用于大规模场景以及小物体重建，能够处理复杂表面；③重建效果依赖德劳内三角剖分的质量，容易受到噪声和外点影响；④通常需要结合网格细节优化获取更加精细的表面细节。

4.2 基于符号距离场的表面重建方法

基于符号距离场的表面重建流程如图25所示。

Fig.25 Surface reconstruction based on symbol distance field图25 基于符号距离场的表面重建流程

Fig.26 Uniform（left）and non-uniform（right）spatial division图26 均匀（左）与非均匀（右）的空间划分

4.2.1 空间划分

空间划分主要是用于对空间中的隐函数进行离散化，以便于对划分区域的每个顶点计算一个符号距离值。空间划分方式可以采用均匀和非均匀两种。均匀划分是将空间划分为大小相等的体素网格（Grid），非均匀方式是用八叉树（Octree）结构将空间进行划分，即在点密集处空间划分较细，树的顶点较小；点稀疏处空间分辨率较低，树的顶点较大，点的分辨率可以根据三维点到相邻点的平均距离确定。

4.2.2 符号距离场构建

文献［49］提出一种局部的符号距离场构建方法，用符号距离函数（Signed Distance Function，SDF）计算空间中各处的符号距离值，然后提取等值面作为物体表面。

符号距离函数是某度量空间中点X 到某一边界的距离关于X 位置的函数，当X 在边界内时，SDF 为正；当X 在边界外时，SDF 为负。如图27所示，0所在位置即可认为是物体表面。

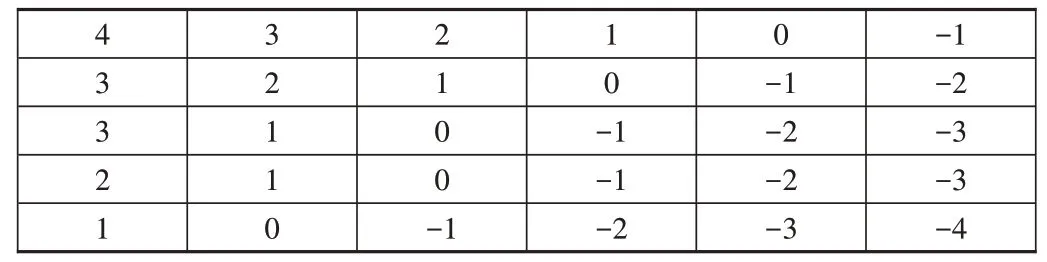
Fig.27 Diagram of symbol distance function图27 符号距离函数示意图

文献［49］所用的符号距离函数为：

即在点x附近邻域取i个点pi，在pi处建立局部坐标系（x轴与pi点的法向量ni方向相同，y轴与z轴分别与x轴垂直），再利用旋转矩阵Ri将x旋转到局部坐标系下，得到xi=Ri·(x-pi)，对以下基函数f(xi)用ciwi(xi)加权计算即可得到点x处的符号距离值，其中，wi(xi)权重函数，ci为点pi的置信度（NCC 值）。

局部符号距离场结果如图28所示［49］。

Fig.28 Boundaries computed by symbolic distance function图28 符号距离函数计算边界

文献［50］提取了一种全局的符号距离场构建方法，将有向点看作是对隐函数梯度的采样，如图29 所示。全局的方法优点是鲁棒，能够很好地处理噪声和空洞，缺点是计算量大，需要求解大规模的方程。

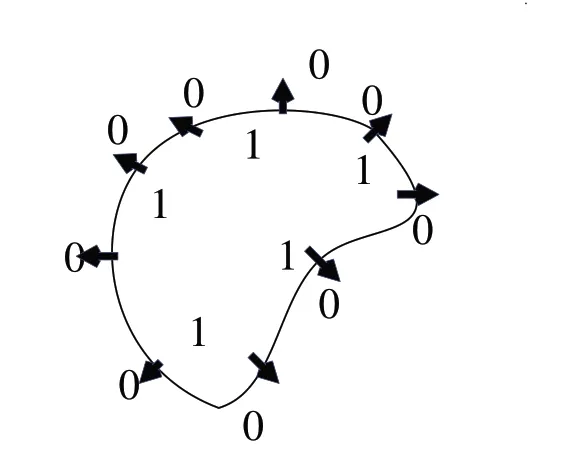
Fig.29 Poisson surface reconstruction图29 泊松表面重建

4.2.3 移动立方体算法生成表面

移动立方体算法（Marching Cube）最早由文献［51］提出，在得到每个体素8 个顶点的符号距离值后，通过插值方法生成三角形面片，每个顶点有两种状态，总共有256种，但由于反转状态不变，因此可以减少一半，为128 种，再根据旋转不变形，又可以减少到14 种情况。可以认为这14 种类似于基，经过旋转、反转可以得到256 种状态所对应的结果（其中3种情况），如图30所示。

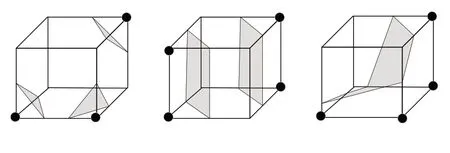
Fig.30 Surfaces generated by marching cube method图30 移动立方体法生成表面

文献［52］提出一种专门针对八叉树的方法，旨在解决相邻节点分辨率不一致时可能出现的裂缝问题。通过引入一组从八叉树的拓扑推导而来的二叉边树，可以在不约束八叉树的拓扑结构或修改顶点值的情况下，直接提取水密的多边形网格。

文献［53］提出一种将平面投影与区域生长相结合的表面重建方法，降低了表面重建复杂度。文献［54］用统计滤波器对点云简化去噪，并建立点云间拓扑结构，缓解了重建表面粗糙、孔洞等问题。

5 纹理图像创建

为了生成更加逼真的场景和物体，可以对生成的三维模型贴上纹理图像。文献［56］在文献［55］的基础上提出创建纹理图像管线，主要分为如下步骤：视角选择、全局颜色调整、泊松图像编辑。

5.1 视角选择

为每个三角面片选择唯一的视角，用于获取纹理信息，视角的选择应当考虑到以下因素：图像尺度、图像细节丰富程度、图像可视性、邻域平滑性。具体方法为：将视角选择建模成多标签分配问题，为每一个三角形分配一个标签（视角），在网格上建立马尔可夫随机场，每个面片代表一个顶点，通过优化能量函数得到最优视角选择。能量函数分为数据项Edata和平滑项Esmooth，即：

其中，Fi表示第i个三角面片，li表示分配给它的视角标签，数据项Edata通过三角面片对应的二维图像上三角形内的平均像素梯度进行度量，旨在选择图像分辨率较大的视角；平滑项约束希望相邻三角形有相同的视角以保持邻域的平滑性，从而减少缝隙，为后续处理提供便利。选择好对应的视角后，即可将网格投影到对应视角的可视图像上，截取对应图像作为纹理图像，经过坐标归一化处理后，即可作为三角面片的纹理坐标，后期通过纹理坐标可找到纹理图像上对应的贴片。

5.2 全局颜色调整

由于不同视角间存在相机曝光或者光照差异导致不同的纹理图像边界处存在明显缝隙，因而要为边界处的每个像素添加一个颜色调整量使得缝隙处的颜色差异尽量小，纹理图像内部相邻像素的调整量尽量相似。

具体方法：首先为三角面片的每个顶点对应像素添加一个调整量，再通过插值方式得到三角面片内部对应的每个像素的调整量，然后将缝隙处的顶点拆分成n个（n为标签个数），对其施加n个调整量，最后通过优化以下能量函数得到调整后的结果：

其中，Es(g)的约束目标是使不同视角下同一顶点调整后的颜色尽量接近，而Ei(g)的约束目标是使相同视角下不同顶点的调整量尽量接近，λ为可调整系数。

5.3 泊松图像编辑

对于缝隙比较严重的区域，全局颜色调整并不能保证完全去除缝隙，还需要作进一步处理。泊松图像编辑算法原理为对前景图像和背景图像进行混合，使得融合后的图像满足：边界上的像素值与背景图像相同，前景区域内的梯度与引导梯度场相同［57］。

这种方法最初用于图像融合。如图31 所示［57］，要将源图像g插入到目标图像S的区域Ω中，该区域具有边界∂Ω，目标图像的像素值与像素坐标的关系可表示为一个函数f*，而合成后的图像在区域Ω中的像素值与像素坐标关系用f描述，v代表一个引导梯度场，实际上是指源图像g的梯度。其中，g、S、Ω、∂Ω、f*、v都是已知量，而f是待求函数（融合后在区域Ω 中的图像）。

Fig.31 Poisson image fusion图31 泊松图像融合示意图

优化的函数为：

其中，∇f表示图像融合后f的梯度，优化目标是使f边界上的像素值与背景图像相同，f的梯度与源图像g的梯度v相同。求解以上优化函数可以转化为求解以下泊松方程：

其中，Δf表示f的拉普拉斯滤波结果，在某一像素处可以用相邻像素线性表示，而divv==Δg，于是可将泊松方程转化成Δf=Δg，用线性方程快速求解。泊松图像融合效果如图32所示［57］。

Fig.32 Effect of Poisson image fusion图32 泊松图像融合效果

进行全局颜色调整后，只需在缝隙处进行泊松编辑即可得到边界平滑的纹理图像。此外，可以通过控制内部区域的范围（如由当前边界往前景区域扩充3 个像素作为前景进行计算），从而减少计算复杂度。泊松图像编辑还应用于图像拼接，如文献［58］提出一种对无人机影像的拼接技术，取得了良好效果。

6 结语

与深度学习的三维重建方法相比，基于图像的三维重建算法流程清晰，具有明确的中间结果，是典型的“白盒”模型，不需要预训练神经网络，对各种场景和物体适应性强，可以全流程优化改善，增强实现效果。但也存在计算速度慢、过分依赖于图像特征点，且对弱纹理、朗伯面、纤细物体重建效果不佳等缺点。

鉴于以上不足，以下工作可能取得重要进展：①图像数据与视觉里程计、激光雷达等多传感器信息融合，不再依赖于纯图像，增加信息来源，既提升运算速度，又提高计算精度；②与深度学习方法相结合，实现在没有图像特征点或匹配对很少的情况下，得到相机的相对位置关系，并对弱纹理区域、朗伯面重建具有鲁棒性；③算法软件提升与基于GPU 的硬件加速相结合，提升算法运行效率，逐步实现大场景下的实时三维重建。