考虑岩体膨胀效应的高地应力软岩隧道稳定性控制研究——以米林隧道为例

陶 琦

(中铁十九局集团第六工程有限公司, 江苏 无锡 214028)

0 引言

软岩是指在特定地质环境条件下能够产生显著的可塑性变形的软弱岩体力学介质[1-2]。对于穿越深部高地应力软弱地层的隧道,由于深部岩体突出的“高温、高地应力与高渗透压”地质特征,隧道施工过程中软岩大变形频发,加剧了隧道开挖与支护难度,是隧道工程中亟需解决的关键问题[3-4]。明确深部软岩隧道围岩压力演化机制,制定有效的软岩大变形关键控制技术,对于隧道稳定与安全建设具有重大意义。

目前,已有众多国内外学者对此展开了研究并取得了一定有益成果。在软岩大变形产生机制研究方面,刘志春等[5]基于隧道大变形实测数据指出,高地应力作用下围岩对支护结构的作用力以形变压力为主; 何满潮等[6]通过泥质软岩吸水试验,指出泥质软岩隧道产生大变形的主要原因在于软岩吸水膨胀变形; Cao等[7]、韩常领等[8]、李磊等[9]、Yang等[10]通过分析地应力对支护结构的挤压作用机制,得出挤压大变形隧道围岩对支护的作用以形变压力为主的结论; 孟陆波等[11]基于大量高地应力软岩隧道变形案例,在形变压力作用机制下,对诱发非对称大变形的因素进行分析,并在此基础上提出了非对称挤压大变形的优化分级法; Anagnostou[12]从围岩变形产生机制角度出发,将大变形归结为围岩卸荷应力重分布而引发的塑性变形及围岩吸水膨胀大变形。

在软岩大变形控制技术研究方面,Bonini等[13]对穿越极软页岩和片岩地层的法国Saint Martin La porte 隧道挤压大变形进行研究,提出了“掌子面超前核心土预加固+长锚杆+全断面可伸缩性钢拱架+初期支护”的软岩多重联合支护技术,并取得成功应用; 李国良等[14]依托穿越高地应力极软千枚岩地层的乌鞘岭隧道,针对隧道岭脊段所发生的大变形现象,制定了“短台阶+超前小导管+锚杆+重型钢拱架+横向钢管+适时二次衬砌”的复合支护系统; 文献[15-17]在探明木寨岭隧道软岩大变形的岩体流变机制基础之上,提出围岩变形分阶段控制思想,形成了超前注浆小导管+锚网喷+高刚度拱架的综合控制技术; 文献[18-19]通过现场试验对西成高铁阜川隧道软岩大变形控制技术进行研究,提出了双层钢拱架支护与喷射混凝土封闭的围岩变形支护技术并取得成功应用。

基于以上分析,对于软岩隧道大变形产生机制与控制技术研究,大多学者仅考虑围岩的挤压作用。对于穿越高地应力膨胀软岩地层的深埋隧道,由于隧道围岩开挖荷载的作用,导致围岩卸荷,产生自由面,围岩湿度发生变化,进而引发围岩产生严重的挤压变形与膨胀变形。因此,对于穿越该特殊类型地层的隧道,在围岩对支护结构的作用力中,形变压力与膨胀压力占主导地位,而现有研究在支护设计中往往仅考虑形变压力而忽略或低估了膨胀压力的作用,因此存在一定局限。

本文以米林隧道为工程依托,基于岩体弹塑性力学,推导出岩体膨胀压力方程,结合卡斯特纳尔算式,建立隧道开挖断面变形与塑性区半径之间的函数解,从而确定以断面径向位移为自变量的膨胀压力与形变压力函数式,采用收敛-约束法绘制出考虑膨胀压力的围岩特征曲线与初期支护特征曲线,分析围岩与支护结构的相互作用规律,确定二次支护的合理支护参数。通过理论分析、数值模拟与现场应用多方面验证支护方案的安全性。

1 米林隧道软岩大变形特征

1.1 工程概况

米林隧道位于林芝市米林县扎绕乡,进口里程为D2K378+111,出口里程为D2K389+671,隧址区位于念青唐古拉山与喜马拉雅山之间的藏南谷地高山区。隧道最大埋深为1 200 m,洞身主要穿越砂质泥岩、英安岩、黄泥岩等地层。隧址区地下水主要为第四系松散孔隙水,其透水性强、渗透系数大,对混凝土结构无侵蚀性。正洞采用两台阶法施工,隧道施工至DK246+100～+695段时,围岩产生大变形,现场初期支护变形收敛大,出现开裂脱落、钢架扭曲等情况,变形较严重的断面有: DK246+137,拱顶沉降累计值为499.8 mm,水平收敛累计值为369.1 mm; DK246+161,拱顶沉降累计值为378.1 mm,水平收敛累计值为296.6 mm; DK246+171,拱顶沉降累计值为391.2 mm,水平收敛累计值为268.1 mm。

根据勘察资料,该段隧洞埋深达833.7 m,洞身围岩主要为Ⅴ级黄泥岩,隧址区域性断裂构造发育,节理裂隙发育,节理间距1～2 m不等,呈密闭—微张状,延伸性较好,节理面由粉质黏土或粉土充填。岩样成分检测结果显示,岩样组成成分中蒙脱石、伊利石等黏土矿物质量分数为16.4%～22.3%,自由膨胀率达到32.7%,阳离子交换量为40.74 me/100 g、干燥饱和吸水率为51.04%。通过采用YYP-50岩石膨胀压力试验仪开展室内试验,测得岩体极限膨胀力为387.5 kPa。因此,在米林隧道的围岩压力计算中,仅考虑由于挤压荷载引发的形变压力以及围岩固有膨胀属性所引发的膨胀压力。该区段地下水发育,开挖掌子面局部湿润,个别区段有水浸出,隧道工程概况如图1所示,由工程资料获得的围岩力学参数见表1。

图1 米林隧道工程概况

表1 米林隧道围岩力学参数

1.2 地应力等级的确定

为了解隧道原始地应力场的分布特征,对应正洞里程DK246+150处布置地应力测试水平钻孔、铅直钻孔各1个,在铅直孔、水平孔深度范围内,分别成功获得8、11段实测岩体水压致裂地应力试验曲线,水平钻孔与铅直钻孔地应力分布情况如图2所示。

根据图2的地应力实测结果,铅直钻孔最大水平主应力平均值为36.43 MPa,水平钻孔最大主应力平均值为41.09 MPa。文献[20]对岩体初始应力状态定量值与定性值的对应关系进行了明确界定,如表2所示。

米林隧道岩石饱和单轴抗压强度σc=17.4 MPa,隧道初始地应力σmax=41.1 MPa,则岩体初始应力状态定量值为σc/σmax=0.42。根据表2确定米林隧道DK246+100～+695段为极高地应力区。

(a) 铅直钻孔

(b) 水平钻孔

表2 初始应力状态定量值与定性值关系

1.3 隧道围岩大变形等级的确定

文献[21]根据岩体强度理论计算值σb与最大主应力σmax对围岩大变形进行分级: 当σb/σmax=0.25～0.5时,围岩变形等级为Ⅰ级;当σb/σmax=0.15～0.25时,围岩变形等级为Ⅱ级;当σb/σmax<0.15时,围岩变形等级为Ⅲ级。根据Mohr-Coulomb屈服准则,由黏聚力c和内摩擦角φ确定围岩强度理论计算值σb的关系式见式(1)。

(1)

米林隧道围岩黏聚力c=0.7 MPa,φ=39°,计算得岩体强度σb=2.93 MPa,则岩体强度应力比σb/σmax=2.93/41.1=0.07<0.15。根据文献[21]中的围岩变形评价标准,米林隧道DK246+100～+695段围岩存在Ⅲ级大变形的风险。

2 膨胀软岩隧道的围岩压力演化机制

对于穿越高地应力膨胀软岩地层的深埋隧道,围岩对支护结构的作用力主要来自于开挖卸荷作用引发的形变压力与围岩由于湿度发生变化而产生的膨胀压力。因此,对于穿越该特殊类型地层的隧道,在支护设计中主要考虑形变压力与膨胀压力的作用效应。

2.1 塑性区形变压力Kastner算式

卡斯特纳尔(Kastner)公式[22]是圆形洞室形变压力的经典计算式,卡斯特纳尔形变压力pi计算公式为:

(2)

2.2 塑性区围岩膨胀压力求解

开挖一半径为R0的圆形隧道,围岩形成半径为Rp的塑性区,对于距离隧道中线L(L>R0)位置处的岩体,岩体湿度分布函数为W=W(L),膨胀系数为α,开挖导致围岩湿度场失衡,岩体除了产生弹性变形之外,还将产生附加正应变αW,采用应力分量表示的平面膨胀压力-应变方程为:

(3)

式中:μ为泊松比;σr、σθ、εr、εθ分别为径向、切向应力分量,径向与切向应变分量;由平面膨胀压力-应变方程(3)解出平面应力问题的平衡微分方程:

(4)

式中:τrθ为剪应力分量;r′、θ′分别为岩体微单元转角及半径。

隧道开挖后围岩由三向应力稳定状态转换为二向应力不平衡状态。由于压力梯度的影响效应,地下向隧道空间迁移的倾向性增强,围岩自由面上湿度最大,湿度呈向围岩深处递减的分布规律,湿度分布函数表示为W(L)=Wmax(R0/L)λ(Wmax为岩体最大湿度变化量,λ为岩体渗透系数)。将平面应力问题简化为轴对称问题,采用位移法求解平面应力问题的平衡微分方程(4),得:

(5)

式中:A、B为积分常数;R为围岩半径。

联合径向应力σr与径向剪应力τr的边界条件(σr、τr)L=R0=(σr、τr)L→∞=0与湿度分布函数,解出岩体膨胀压力分量:

(6)

当取L=Rp时,则推导出塑性区内岩体膨胀压力

(7)

2.3 径向位移发展过程中形变压力与膨胀压力解

由式(2)与式(7)的解析式可知,影响形变压力与膨胀压力的一个公共因子为塑性区半径Rp。为直接揭示围岩变形过程中形变压力与膨胀压力的演变趋势,以塑性区半径为中间过渡变量,通过建立塑性区半径与围岩位移之间的函数关系,确定形变压力与膨胀压力特征曲线解。

岩体由于开挖卸荷而产生湿度变化ΔW,岩体进一步产生附加应变αΔW,则平面应变-应力关系为:

(8)

式中:ψ为塑性模数,弹性区ψ=1。

(9)

(10)

(11)

联立函数式(2)、式(7)与式(11),消去断面塑性区半径变量,则建立出形变压力pi与膨胀压力pr的特征曲线解:

(12)

(13)

3 隧道围岩与支护结构相互作用关系

3.1 收敛-约束法

收敛-约束法[23-24]主要由纵剖面变形曲线(LDP)、支护特征曲线(SCC)以及围岩特征曲线(GRC)组成。基于收敛-约束理论评价隧道围岩稳定性的关键在于: 明确围岩特征曲线(GRC)与支护特征曲线(SCC)之间的相对变化趋势,确定合理支护时机与支护参数。收敛-约束法原理如图3所示。

u0为支护设置时围岩初始位移;ueq为支护稳定时所产生的弹性位移;uel-i为支护最大弹性位移;umax为支护最大位移。

图3 收敛约束法原理图

Fig. 3 Schematic of convergence constraint method

根据收敛-约束理论,隧道支护结构所提供的极限承载力为:

pmax=K·(uel-i-u0) 。

(14)

式中:K为支护刚度系数,即支护特征曲线的斜率; 当u0umax时,支护系统破坏。

3.2 隧道围岩稳定性分析

3.2.1 GRC、SCC曲线求解与围岩稳定性分析

本文采用文献[25-26]方法计算初期支护各子支护结构的支护刚度K与极限承载力pmax,再通过叠加得到支护系统的总极限承载力。本隧道为马蹄形隧道,断面高度h=11.94 m,跨度b=13.08 m,根据文献[27],求得隧道等效圆半径R0=6.25 m。未按Ⅲ级大变形进行设计的隧道原始支护采用锚喷+可缩式钢架的复合支护形式,钢架钢材为I28a型,每断面设置8个可缩接头,分别设置于拱顶,左、右拱肩,左、右拱腰,左、右拱脚与拱底位置处。混凝土喷射厚度tshot=36 cm,锚杆长度lbol=8.0 m,间排距St×Sl=1.2 m×1.0 m,钢架间距d=0.8 m,初期支护材料参数如表3所示。根据支护材料参数求得原始支护系统支护特征曲线参数如表4所示。

表3 初期支护材料参数

将岩体力学参数(见表1)及初始地应力p0代入式(12)与式(13)进行求解,分别计算得到形变压力以及在形变压力基础上考虑岩体膨胀压力的围岩特征曲线。其中,pi+pr特征曲线的求解方法为,将同一径向位移u所对应的pi特征曲线与pr特征曲线叠加而成[28]。根据表4支护特征曲线参数计算结果求得米林隧道初期支护特征曲线。基于收敛-约束法原理,将两曲线绘制于同一坐标系中以分析米林隧道围岩与初期支护相互作用规律,如图4所示。

表4 原始支护特征曲线参数

图4 围岩与初期支护特征曲线

由图4计算结果,当不考虑膨胀压力作用条件下,围岩变形至0.212 m时GRC曲线与SCC曲线相交于平衡点1,围岩在支护结构屈服过程中达到稳定;而当在形变压力基础之上考虑膨胀压力作用时,理论计算平衡点后移至873 mm,远超围岩预留变形量。根据现场监测,隧道DK246+130～+260段围岩变形最大值达到831.5 mm,现场支护破坏状况如图5所示。因此,对于深部潜在变湿条件下的软岩隧道,仅考虑形变压力而设计的支护结构不能维持围岩稳定,考虑膨胀压力的工况更符合实际。

(a) (b)

3.2.2 膨胀压力占比演化规律

开挖致使围岩由原始三向应力稳定状态转变为二向应力不平衡状态,由于压力差的作用及开挖产生的自由面,在形变压力作用下,围岩塑性区持续扩大,岩体内部逐渐产生裂隙导致水分扩散,围岩湿度发生变化,膨胀压力pr在形变压力pi卸除过程中开始显现,此时断面变形为93 mm。根据图4所示,由于前期裂隙发育程度较轻,此时岩体产生的膨胀压力pr仅为0.04 MPa,pr占比仅为3.3%;在围岩径向位移达到93 mm前,形变压力pi是支护结构的主要压力源;当围岩径向位移持续释放,由90 mm增至300 mm时,形变压力急剧释放,围岩裂隙加速扩张,隧道径向范围内水分扩散加快,岩体湿度差剧增,膨胀压力pr增长迅速,占比提高到15.8%;围岩变形发展达到530 mm时,初期支护结构破坏,此时不考虑膨胀压力pr,围岩施加于支护上的形变压力为0.82 MPa,当考虑膨胀压力pr的作用时,支护承载压力上升至为1.37 MPa,膨胀压力占比增加至40.1%。计算结果表明,在断面径向位移释放过程中,形变压力与膨胀压力呈现出此消彼长的演化规律,即在围岩位移释放过程中,形变压力递减而膨胀压力呈现出上升趋势。基于上述计算结果分析,在对支护结构的作用力中,虽然形变压力占据主导地位,但膨胀压力仍不可忽略,膨胀压力pr占比演化规律如图6所示。

图6 膨胀压力占比演化规律示意图

4 隧道围岩支护优化分析

综上所述,要实现控制围岩大变形的目的,其核心在于确定围岩位移释放极限值upeak以协调形变压力与膨胀压力的动态变化关系。采用柔性初期支护对形变压力进行部分卸除,当断面变形至upeak时,采用高刚度、高强度的补强支护及时约束围岩过度变形,从而达到限制膨胀压力过度增大的目的。

4.1 隧道支护优化-钢架二次补强支护时机

隧道稳定性控制对二次支护提出了安全储备要求。Oreste[26]采用安全系数Fs评价支护安全储备,Fs算式为Fs=pmax/peq。式中:pmax为支护极限承载力;peq为弹性支护抗力。

选取围岩径向位移u=0.20、0.25、0.30、0.325 m 4种工况,对最佳位移释放上限值upeak进行求解。本文采用I25a、I25b钢架作为隧道的二次支护进行稳定性计算分析。对于围岩位移上限值upeak的确定,仅选用间距为0.8 m的I25a钢架进行计算即可,钢架参数见表5。求得I25a钢架二次支护最大承载力pmax=0.232 MPa,支护刚度系数K为33.289 MPa/m,弹性形变为6.97 mm。根据二次支护特征曲线参数,绘制出4种upeak条件下的二次支护特征曲线,如图7所示。

图7 各支护时机条件下补强支护特征曲线

由图7可知,采用I25a型钢架作为二次支护,支护系统(初期支护+二次钢架补强支护)极限承载力为1.403 MPa,在围岩位移释放上限值upeak取0.20 m与0.25 m 2种工况时,二次支护特征曲线均未与围岩特征曲线相交,即二次钢架设置过早,形变压力的释放量过小,围岩总压力大于支护极限承载力,支护结构破坏。当upeak分别达到0.300、0.325 m时施作二次支护,二次支护特征曲线弹性段均与围岩特征曲线交汇,且弹性支护抗力peq分别为0.224、0.213 MPa,安全系数Fs分别为1.005、1.014,满足围岩稳定性要求。因此,确定米林隧道二次支护的最佳施作时机为upeak=0.325 m(Fs=1.014)。

4.2 加强支护参数的确定与验算

对隧道DK246+270～+355大变形段支护进行优化与围岩稳定性验算。本文分别采用I25a、I25b钢架为二次支护。钢架弹性模量Est、横截面积Aset、屈服强度σst、横截面高度hset参数见表5。二次支护工况与支护特征曲线参数计算结果见表6。

表5 钢架材料参数

表6 二次支护工况及支护特征曲线参数

根据位移释放上限值upeak及各工况二次支护结构的支护极限承载力、支护刚度系数及弹性变形等参数,绘制二次支护特征曲线,如图8所示。确定不同工况二次支护的安全系数,选取安全系数高的支护工况作为米林隧道二次支护系统。

根据计算结果求得各工况下支护的极限承载力pmax、弹性支护抗力peq及安全系数Fs,如表7所示。

由表7可知,工况3支护破坏,工况1、2、4、5、6的支护系统均能实现围岩稳定,且工况4安全系数最高。综上,选取米林隧道二次补强支护参数为I25b型钢架、间距0.7 m。

4.3 米林隧道稳定性数值分析

通过理论计算初步确定了满足米林隧道稳定性的初期支护与二次支护系统。为进一步验证支护设计的合理性,采用FLAC3D数值模拟对米林隧道围岩稳定性进行分析,以确保支护方案更加安全可靠。

(a) 钢架间距d=0.7 m

(b) 钢架间距d=0.8 m

(c) 钢架间距d=0.9 m

表7 各工况二次支护安全系数Fs

4.3.1 隧道数值模型与边界条件

选取隧道DK246+270～+355进行分析,隧道模型尺寸为150 m×150 m×85 m,如图9所示。围岩力学模型为Mohr-Coulomb弹塑性本构模型,岩体力学参数如表1所示。围岩热力学模型采用各向同性的热传导模型,模型的前、后、左、右、下边界均为法向固定绝热边界,上边界为变温边界且与右边界分别施加竖向荷载σv与水平荷载σh,其值大小为41.09 MPa,模型初始温度场T1=0 ℃。

图9 隧道模型示意图(单位: m)

本文中锚杆与混凝土支护结构分别采用杆单元与壳单元进行模拟,材料参数见表3。对于钢架支护的数值模拟,将钢架按抗弯刚度等效为FLAC3D中的梁(beam)实体单元,等效梁单元厚度等于喷射混凝土厚度tshot,宽度与型钢翼缘宽度一致,等效算式为:

EsIs=E′I′ 。

(15)

式中:Es与Is分别为钢架实际弹性模量与抗弯惯性矩;E′与I′分别为钢架等效弹性模量与等效抗弯惯性矩。

4.3.2 围岩膨胀压力模拟

FLAC3D热力耦合(单向耦合计算模型)是通过温度改变引起单元的应变而实现的,温度引起的应变增量Δεij与温度改变量ΔT的函数关系为:

Δεij=βΔTδij。

(16)

式中:β为温度线膨胀系数,1/℃; ΔT为温度变化量,℃;δij为kroneeker记号。

(17)

(18)

根据现场勘测资料,米林隧道围岩最小含水率为12.7%,最大含水率为32.5%,则湿度变化ΔW=19.8%,取最小含水率为12.7%时的对应温度T1=0 ℃,最大含水率为32.5%时的对应温度T2=100 ℃,则求得对应岩体温度线膨胀系数β=0.198。

4.3.3 模拟计算结果与分析

为减小模型边界效应的影响,取模型中间段即隧道DK246+310里程断面的计算结果进行分析,计算求得不同压力组合下围岩位移云图与初期支护锚杆应力云图如图10和图11所示。

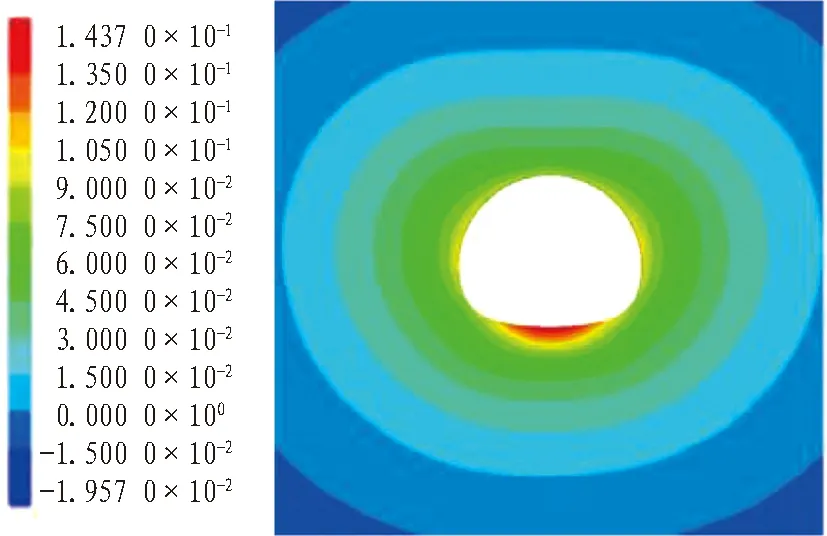
(a) 围岩位移(单位: m)

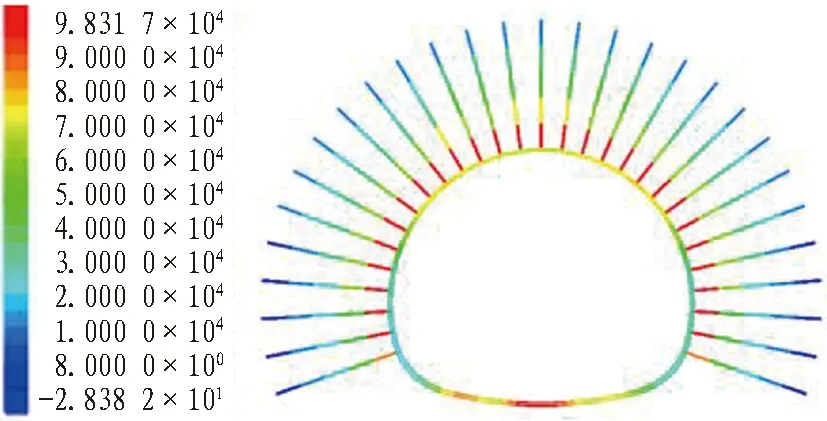
(b) 锚杆应力(单位: Pa)

根据图10和图11的计算结果,基于收敛-约束法所得的米林隧道围岩稳定性理论计算结果与数值模拟计算结果一致。以最不利荷载条件,即同时考虑形变压力与膨胀压力进行分析,围岩达到平衡时最大变形量为288 mm,锚杆最大应力为0.107 MPa,应力与位移峰值均产生于拱顶位置。而优化设计支护结构(工况4)最大承载力为1.464 MPa,大变形段围岩预留变形量为0.325 m,因此优化支护满足围岩稳定性要求。

4.3.4 隧道二次支护施作与监测

根据理论计算与数值模拟验证了优化支护方案的合理性。工程现场采用该方案对隧道进行支护,第2层钢架现场布置与监测点布置如图12所示。

在米林隧道DK246+270～+355段第2层钢架支护设置完毕后对围岩变形进行监测,选取隧道DK246+310为监测断面,断面上共设置8个监测点,监测数据读取频率为2次/d,监测周期为30 d,监测点布置及监测结果如图13所示。

(a) 围岩位移(单位: m)

(b) 锚杆应力(单位: Pa)

图12 第2层钢架现场布置和监测点布置图

图13 断面监测点布置及监测结果

由监测结果可知,隧道DK246+310断面在第2层钢架施作后,围岩最大变形产生于拱顶位置。钢架施作23 d后拱顶累计变形最大为56.1 mm,随后围岩变形速率降低并趋于0,钢架设置30 d后围岩几乎不再产生变形,米林隧道大变形得到有效治理。

5 结论与讨论

1)高地应力膨胀软岩隧道大变形产生的原因为在隧道支护设计中忽视了围岩膨胀压力的作用。开挖扰动引发地应力场与湿度场重分布,围岩对支护结构作用力除形变压力之外还有膨胀压力,仅考虑形变压力的支护不能维持隧道稳定,考虑膨胀压力的计算工况更符合实际状况。

2)形变压力与膨胀压力在断面径向位移释放过程中呈现出此消彼长的演化规律,即在围岩位移释放过程中,形变压力递减而膨胀压力呈现出上升趋势。

3)以围岩断面径向位移u为划分标志,围岩膨胀压力pr与形变压力pi的动态演化规律可分为3个阶段: 第1阶段u=0～93 mm,该阶段围岩对支护结构压力以形变压力pi为主导; 第2阶段为u=93～300 mm,此阶段膨胀压力开始增长,在形变压力pi基础之上考虑膨胀压力pr时,支护承载压力增大为1.156 MPa,pr占比达到29.7%; 第3阶段u=300～530 mm,此阶段形变压力为0.82 MPa,膨胀压力pr加速增长达到最大值,支护承载压力增大为1.37 MPa,膨胀压力占比达到40.1%。

4)针对米林隧道软岩大变形,通过收敛-约束法确定以柔性初期支护使围岩径向位移达到upeak=0.325 m时采用间距d=0.7 m的高刚度I25b钢架进行补强支护。通过理论计算、数值模拟与工程应用多方面验证了优化支护方案的可行性,米林隧道软岩大变形得到有效控制。

本文基于岩体弹塑性力学与连续介质理论,推导出软岩在变湿条件下的膨胀压力计算式,结合求解形变压力的卡斯特纳尔经典公式,对隧道围岩压力进行求解,明确了围岩压力变化规律,为设计出合理的支护系统提供了指导。但是,在引发软岩大变形的围岩压力类型中,本文只考虑了形变压力与膨胀压力的作用,对于其他,如穿越断层破碎带等类型岩层的隧道,在支护设计中是否需要在此基础之上进一步考虑围岩松动压力对隧道稳定性的影响,需要进一步研究。