基于机械激振方式进行高地应力软岩隧道应力释放效果研究

李建斌, 李新宇, 朱 英, 唐小微

(1. 中铁高新工业股份有限公司, 北京 100000; 2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024; 3. 中铁工程装备集团有限公司, 河南 郑州 450016)

0 引言

21世纪已经步入隧道与地下空间工程的发展时代[1],隧道在交通网络建设中具有举足轻重的地位,特别伴随着高铁和城市铁路的不断修建,以及国家对西北地区和西南地区的大力建设,使得隧道的开挖深度与长度不断增加,所面临的施工地质条件也随之变得越来越复杂,高地温、强富水、挤压性围岩和有害气体等复杂条件的特殊隧道逐渐增多,给实际建设带来一系列问题。

在深部隧道建设中主要存在突水突泥、岩爆、塌方冒顶以及软岩大变形等问题[2]。其中软岩大变形一般出现在变质岩、破碎断层、煤系地层等低强度围岩中[3],变形速率达到10 cm/min至5 m/min,围岩在快速收敛过程中会导致支护的变形和破损,阻碍施工正常进行,严重时甚至发生工程事故。大变形的形成机制[4-6]主要分为2种: 一是塑性挤压大变形,主要是由于开挖后围岩应力在高地应力的基础上重分布,使地应力强度高于软岩自身强度; 二是岩体体积膨胀大变形,主要是由于矿物与水发生反应后产生膨胀造成。综合上述2种变形机制,在隧道施工围岩变形原因中,挤压和膨胀共存,但单纯因为膨胀引起的大变形比较少见,而塑性挤压大变形是引发隧道围岩大变形的主要变形机制。因此,实际工程中会采用各种手段避免因高地应力而引发的变形灾害。

国内外学者针对高地应力进行了大量的研究并已取得丰硕的成果。目前应对高地应力的手段主要分为2种: 1)在开挖中进行预处理,从而完成对应力的卸载,包括钻孔卸压、爆破卸压、水压致裂等; 2)通过改进开挖方式和后续支护结构来抵抗高应力。Diering[7]利用钻爆卸压的方式,对高地应力矿井中井巷掘进过程进行地应力释放处理,发现在使用钻爆卸压法后,巷道的变形量明显减小,有效降低了后续的变形速率,明显提高了巷道支护的安全性,提高了生产开挖的效率。王伟[8]分析了在造穴作用下煤体围岩的应力及塑性区分布机制,同时基于此,结合水流的冲击特性与聚能效应,通过高压水流射入冲孔的方式,形成直径较大的卸压硐室,为卸压后的煤体体积膨胀提供充足的空间,并在钻孔周围形成裂缝网络,达到卸压的目的。陈荣华等[9]针对高地应力地质条件复杂的矿场顶板塌落问题,采用预先注水软化的方式,对一些关键岩层进行预处理,以控制采场压力,并且通过RFPA2D软件分析了不同软化系数和软化厚度对于预防效果的影响。闫鑫[10]针对超前应力释放技术在铁路隧道中的应用不成熟、机制不明确的现状,将原本应用于煤炭领域的超前应力释放技术引入到铁路隧道当中,通过FLAC3D数值计算软件分析了超前应力释放技术对围岩塑性区分布和发展的影响,提出了3种超前应力释放的方式,结合实际隧道的现场试验验证了超前应力释放技术在铁路隧道应用的可行性。Zang等[11]分析了煤矿巷道围岩分别在静荷载和不同扰动强度下的动荷载作用下的变形结果、应力场变化,以及塑性区分布,并针对此结果进行了喷锚与钢筋锚索联合支护方案的优化改良,有效提高了破碎软岩的强度,减少了围岩变形。Duan等[12]采用数值模拟与现场观测相结合的方式,分析了爆破前后衬砌、围岩、锚杆和围岩的稳定性,对爆破扰动后的围岩安全性进行了系统评估,分析了爆破波对围岩的塑性分布影响。Christopher等[13]提出了一种大深度硬岩巷道开挖卸压爆破设计理念,将掌子面的一系列炮孔近似平行于主应力布置,爆破后在整个工作面创建一系列平行和连续的线性裂缝面,使岩石处于峰后加载段状态。杨英明[14]研究了开拓巷道前煤层应力场分布规律,并模拟了岩层的超前钻孔卸压情况,证明超前钻孔不但增大了卸压区的范围,还降低了瓦斯突出风险。

但以上方法都存在一定程度的不足: 钻爆法由于使用炸药,前期准备工作较多,施工安全性难以保障;且具体爆破参数需要凭借施工人员的经验,如果没有准确的参考依据,容易出现二次施工的问题。注水卸压法由于加压设备和排水管道等设备会占用隧道内的施工空间,影响正常施工,同时用水会使隧道内环境变得泥泞,不利于正常施工。钻孔卸压法和切槽卸压法对孔径和槽宽有较严格的要求,孔径与槽宽过小无法良好地释放应力;过宽则会造成掌子面崩坏,威胁施工安全。超前导洞法和平行导洞法需要人工开挖导洞或侧洞,施工过程较危险,同时还会增加施工成本。喷锚强化支护、注浆联合支护和泡沫混凝土支护等方法多集中在对隧道支护的改良,缓解了隧道施工完成初期支护后的变形情况,但存在滞后性,对隧道开挖掘进中即刻产生的大变形问题关注较少,而在实际工程中有相当多的变形问题集中发生在开挖后的较短时间内,这种变形经常会阻碍正常施工,从而影响施工进度。

针对上述方法存在的不足,本文提出采用机械激振方式消除高地应力来改善隧道变形,并以台阶法施工为例,采用数值模拟验证激振法卸除高地应力的可行性。

1 模型建立及振动方式

1.1 建立模型

针对台阶法施工合理建模,如图1所示。采用FLAC3D有限差分软件模拟,对台阶法掘进模型进行计算,其整体尺寸为水平宽度90 m、纵向高度90 m、厚度40 m。台阶每步步长4 m,采用围压20 MPa,对模型上部施加10 MPa压力,在隧道拱肩处左右两侧施加正弦变化式荷载,模型底部采用固定位移边界,模型底部施加三向位移约束,四周采用黏性边界吸收振动能量,模拟无限大边界条件,顶部采用自由边界。岩土体参数如表1所示。

图1 隧道模型

表1 岩土体参数

1.2 激振方式选取

在隧道拱肩两侧进行振动,分别采用相同波形、相差半个周期波形进行激振,以及只对隧道单边进行激振,3种激振方式见表2。激振频率为10 Hz、应力波幅值为100 MPa,通过对比激振所得到的数据来优选激振方式,激振位置示意如图2所示。单边激振力作用面积为2 m2,双边每侧激振力作用面积为1 m2。

表2 激振方式

图2 台阶法激振位置

采用3种不同的激振方式进行振动处理后,后续每开挖4 m进行1次衬砌施作,全程监测隧道顶部的沉降量,形成如图3所示的沉降曲线。通过对比曲线前段应力释放效果来选取更优方式;由于开挖方式采取每开挖4 m进行1次衬砌,施作衬砌材料选用C35混凝土,施作衬砌时部分土体应力得到了释放,故曲线后段呈现V形。对比3种激振方式的沉降曲线可以发现,在隧道拱肩两侧同时进行振动的隧道变形量要小于单边进行振动的隧道变形量,且双边频率错峰相差半个周期的振动所造成的应力释放效果要优于双边完全相同频率振动所造成的应力释放效果。由于双边同频率振动,作用在拱肩两侧的压力在同一时刻达到最大值,使得存在两边的能量相互抵消,消耗了用于应力释放的能量;而错开峰值振动避免了这种能量的损耗,因此该激振方式的释放效果要优于其余的激振方式。

图3 不同激振方式下后续开挖隧道顶部沉降曲线

图4为不同激振方式下竖向应力云图。表3为3种激振方式的应力释放深度。通过对比可发现,单边振动应力释放效果最差,分别比双边错峰和双边同峰激振应力释放深度低13.7%和11.3%。双边错峰和双边同峰激振方式对应力释放效果基本类似,两者相差约2.8%。综合上述分析,在之后的数值模拟中均选择双边错峰振动方式进行激振,达到能量的最佳利用和应力释放效果的最大化。

(a) 双边错峰激振

(b) 双边同峰激振

(c) 单边激振

表3 不同激振方式的应力释放深度

2 激振频率对卸荷效果的影响分析

2.1 寻找共振频率并研究激振频率对结果的影响

针对机械激振这一新型方法,研究激振频率对激振结果的影响。针对岩石体,开尔文体作为一种典型的、具有一定代表性的岩石力学组合模型,也是岩石动力学的基本模型。

加载的谐振激励符合正弦变化规律,振动方程如下:

(1)

式中:m为质量;c为阻尼系数;X为振动位移;k为刚度;F为谐振冲击力;A为谐振冲击力振幅。

位移响应振幅

(2)

式中ω0为岩石的固有频率。

(3)

阻尼

(4)

由式(2)可知,当冲击力频率接近共振频率时,位移响应振幅最大、响应范围最广。因此,在共振频率下,激振对于岩体所造成的扰动效果最大,应力释放的效果最好。为了研究激振频率对激振效果的影响情况,从激振频率1～2 000 Hz取若干工况进行激振模拟,通过与初始地应力状态对比,可以得到在激振完毕后有效的应力释放范围。图5为不同激振频率下距第1台阶掌子面5 m处的竖向应力云图,图中红色区域为应力释放区。通过不同频率下应力释放云图的对比,可以明显观测到: 60 Hz工况下,释放的深度以及效果都远超其余工况,中心竖向应力最低降至4.7 MPa,相比于未振动工况下的12.8 MPa,降低了63%;而10、100、500 Hz 3种工况下的竖向应力相比未振动工况分别降低了40%、56%以及21%,证明在台阶法施工中,共振频率是60 Hz时,共振应力释放效果最好。

将激振处理后结果与初始地应力状态对比,得到在激振完毕后有效的应力释放区深度如图6所示。发现当激振频率小于60 Hz时,应力释放深度范围随激振频率升高而增大,在达到共振频率60 Hz时,应力释放深度范围达到峰值,相较于未激振情况,应力释放提高了107%,相较于其余工况提升了5%～26%。后续随着激振频率增大,应力释放深度范围逐渐减小。证明在台阶法掘进中,共振频率为60 Hz,隧道的应力释放效果最好,深度最大;同时说明当激振频率为共振频率时,应力释放效果最佳。

(a) 10 Hz

(b) 60 Hz

(c) 100 Hz

(d) 500 Hz

不同激振频率下后续开挖顶部沉降曲线如图7所示。由图可发现: 激振频率为60 Hz时沉降量最小。对比未振动工况,在隧道进尺4 m处沉降量下降最大,达到46%;在隧道进尺6 m处隧道沉降量平均降低了43%。相较于其余工况,隧道沉降量降低了10%～23%。在隧道进尺8 m处,隧道的沉降量下降幅度不大,激振造成的应力释放效果已基本消失。在台阶法掘进模型下,选取60 Hz为本模型的共振频率,在共振频率下隧道的超前应力释放效果最优,应力集中区转移深度达到最大,后续开挖隧道沉降量最小。采用其他激振频率进行激振,虽然对于应力释放也存在一定效果,但越是远离这一激振频率,所造成的应力释放效果就越差,隧道的变形量就越大。

图6 应力释放深度

图7 不同激振频率下后续开挖隧道顶部沉降曲线

2.2 土体模量对于最优激振频率的影响

可以发现,土体弹性模量的变化会导致激振频率的变化符合一定数量关系,即激振频率的平方与弹性模量成正比关系,如图11所示。

(a) 20 Hz

(b) 40 Hz

(c) 50 Hz

(a) 80 Hz

(b) 90 Hz

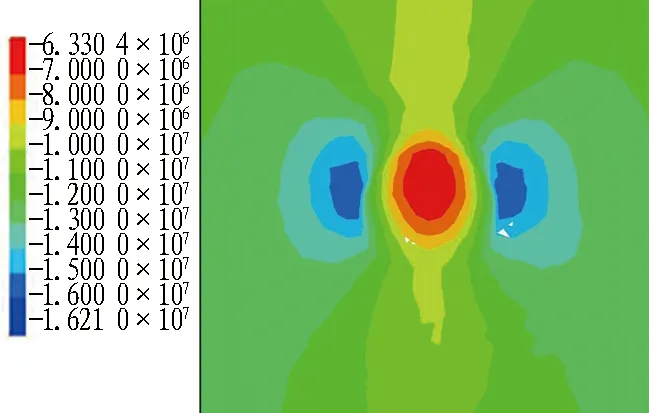
(c) 150 Hz

(a) 80 Hz

(b) 130 Hz

(c) 150 Hz

图11 频率与弹性模量关系曲线

3 激振幅值及时间对卸荷效果的影响分析

3.1 激振时间对于激振效果的影响

针对台阶法得到最优激振频率后,再从大范围激振幅值中选取激振法的最优激振幅值。在激振幅值为10～300 MPa合理选择若干工况进行激振分析,不同激振幅值工况的应力释放深度如图12所示。

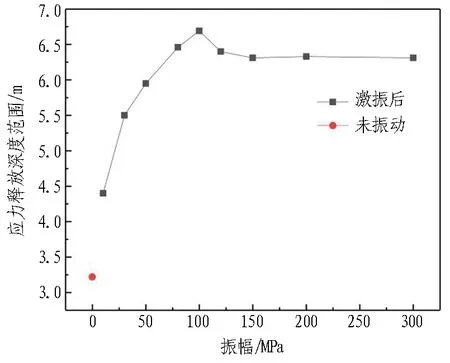
图12 不同激振幅值下的应力释放深度

在激振幅值达到100 MPa之前,应力释放深度随着幅值增大而不断增大,应力释放深度在100 MPa时达到峰值,后续略有降低,但降低幅度较小。

为了进一步探究最优激振幅值,在激振完毕之后对隧道开挖进行模拟,开挖方式与探究频率时相同,对后续隧道开挖以及衬砌施作采用循环分布开挖方式。图13示出不同激振幅值下隧道顶部沉降量。

图13 不同激振幅值下隧道顶部沉降量

由图13可以发现: 激振处理后,隧道顶部沉降量相较于未激振的有明显降低,且激振幅值为100 MPa时隧道顶部沉降最小,对比未振动工况在隧道进尺4 m处沉降量降低最大、达到46.2%,隧道进尺6 m范围内隧道沉降量平均降低了44%。相较于其余工况来说,隧道顶部沉降量降低了10.3%～24.0%,在隧道进尺8 m处位置时,隧道的沉降量降低幅度不大,激振所造成的应力释放效果已基本消失。因此,激振幅值存在一个影响阈值,前半段应力释放效果随着激振幅值增大而增大,但当后续超过某一限值之后,应力释放效果略微下降,虽下降幅度不大,但在实际激振过程中需要合理把控激振幅值,避免造成能量浪费。

3.2 激振时长对于激振效果的影响

为探究时长对激振效果的影响,从激振时长1～40 s取若干工况进行模拟,选择激振幅值为100 MPa、激振频率为60 Hz,不同激振时长下隧道沉降曲线如图14所示。由图可以发现: 在激振10 s后,继续增加激振时长,隧道的应力释放效果基本相同,隧道顶部沉降量不再变化; 在激振10 s后,激振影响范围内的岩体所具有的高应力已充分释放完毕,持续激振也并不会增大卸荷的影响范围。因此,在实际施工中应合理选择激振时长,避免造成能量浪费。

4 最优工况及卸荷效果

综合上述结果,选择激振幅值100 MPa、激振频率60 Hz以及激振时长10 s作为最优激振方式,得到如图15所示的最优组合下隧道顶部沉降曲线。

图14 不同激振时长隧道顶部沉降曲线

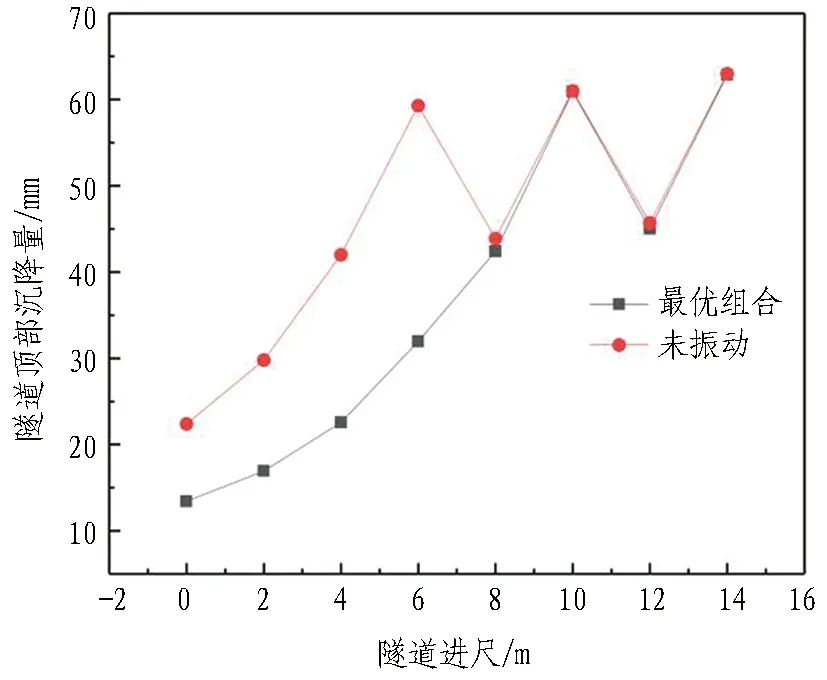
图15 最优组合下隧道顶部沉降曲线

由图15可以发现,隧道顶部沉降量最大可降低46%。因此,以机械激振的方式通过循环施加激振波,扰动原本状态下岩体,同时通过将频率调整至与隧道岩体响应频率相近的方式达到共振状态,从而增加原本岩体响应效果,来提高岩体裂隙扩展,从而达到应力释放,这一方法在台阶法施工中应力释放效果非常好,并且对于隧道后续的开挖是有益的,可以显著降低隧道变形。

5 结论与讨论

1)对比3种激振方式,确定了两侧错峰激振的卸荷效果优于其余2种。

2)当激振频率为系统共振频率时,应力释放效果达到最佳。同时,还发现了土体弹性模量这一参数对于激振频率的影响规律,根据土体弹性模量与共振频率之间的关系,对比最优激振频率的变化,进一步验证激振频率为系统共振频率时,应力释放效果最佳。

3)应力释放效果存在随着激振幅值增大而增大的情况,但存在一个影响阈值;当超过阈值之后,继续增大激振幅值,应力释放效果基本不变,甚至还会略微降低,因此在实际施工中需要合理把控激振幅值,避免造成能量浪费。

4)在激振一定时间后,振动影响范围内的岩体所具有的高地应力已充分释放完毕,此时继续振动并不会增大应力释放的范围。因此在实际施工中需要合理选择激振时长,避免能量浪费,增加施工成本。

目前本文只从数值模拟的角度验证了激振法消除高地应力的可行性,还需要更多的现场数据来验证,并且还需要开发可行的试验方法来验证本方法的适应性和对应力释放的效果。同时,本文仅验证了一小部分的激振布局构思,后续可以参考钻爆法以及平行导洞法等方式,采取侧洞开挖激振的方式以及更多合理的激振方式来对激振法进行开发和研究。