鼠笼弹支轴承外圈优化设计及其性能分析

徐超,马芳,迟杰,于庆杰,薛林林

(中国航发哈尔滨轴承有限公司,哈尔滨 150025)

1 概述

航空涡轴发动机尺寸小,转速高,设计要求大推力、高功重比,转子-支承系统的振动会影响其可靠性,为减小转子振动,主轴轴承设计时采用带有弹性支承和挤压油膜阻尼器附件,如图1所示。支承轴承为双半内圈角接触球轴承,内、外圈分别用螺母固定于芯轴和鼠笼支座上,并用锁片锁紧,承受高压转子的全部轴向载荷和部分径向载荷,载荷通过进气机匣施加。为提高转子临界转速并提供足够的减振阻尼[1-2], 常将鼠笼弹支、 挤压油膜阻尼器和轴承外圈集成为一体,如图2所示。

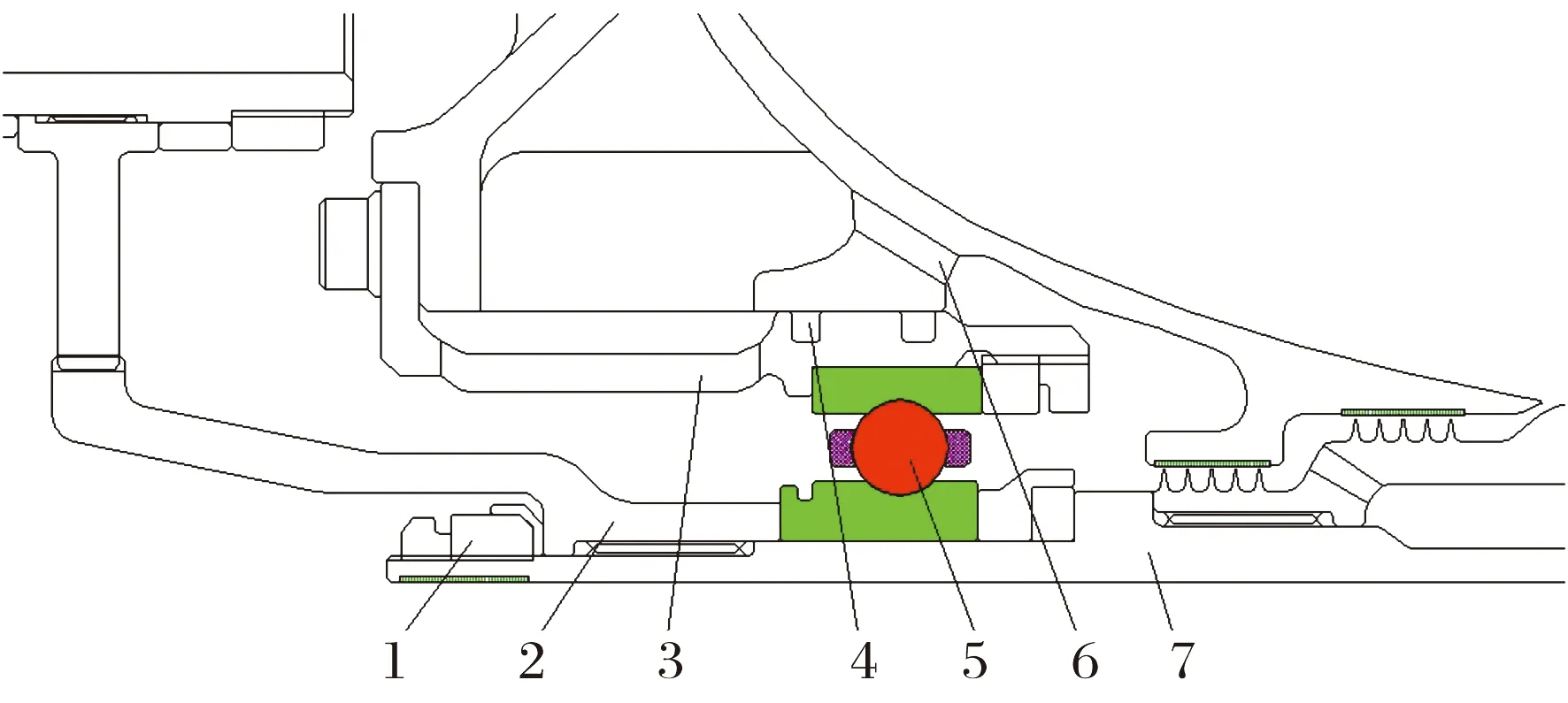
1—压紧螺母;2—传动齿轮;3—鼠笼弹支;4—挤压油膜;5—主轴轴承;6—进气机匣承力框架;7—芯轴。

图2 弹性支承一体化轴承结构

鼠笼弹支轴承刚度对轴承动力学特性有重要影响,设计时应重点考虑[3-5]。此外,鼠笼弹支轴承在进行性能分析时,通常假设轴承套圈为刚性,但鼠笼弹支外圈支座采用螺栓紧固,工作时外圈已发生弯曲变形,故在对其性能进行分析时应考虑外圈柔性的影响[6-8]。

本文以某发动机支点鼠笼弹支轴承为研究对象,建立了鼠笼弹支外圈刚度计算有限元模型,根据其刚度对鼠笼结构参数进行优化设计,并考虑套圈柔性对鼠笼弹支轴承进行性能分析。

2 鼠笼弹支轴承处圈刚度计算

在鼠笼弹支轴承处圈刚度计算时,一般将鼠笼肋条看成两端固定的等截面梁,其支承刚度为[2]

K=NEb2h2/l3,

(1)

式中:N为鼠笼肋条数量;E为鼠笼肋条材料弹性模量;b为鼠笼肋条宽度;h为鼠笼肋条厚度;l为鼠笼肋条长度。

以图2鼠笼弹支外圈为例,外圈材料弹性模量为203 GPa,笼条数为16,笼条长度为19.6 mm,笼条过渡圆角半径R为6.5 mm,笼条宽度为3.1 mm,笼条厚度为1.75 mm。通过(1)式可得K=1.263 7×107N/m,但理论计算未考虑鼠笼肋条根部的过渡圆角,计算值低于实际刚度,现采用有限元法进行计算[9]。建立鼠笼弹支外圈有限元模型[10-12],采用Solid186单元进行网格划分,并对肋条过渡圆角处进行网格细化,共519 705个节点,341 966个单元,约束凸缘一端,在套圈沟道处施加490.33 N的载荷,如图3所示。

图3 鼠笼弹支外圈有限元模型

鼠笼弹支外圈变形和应力云图分别如图4、图5所示,最大变形量为15.421 μm,圆角处的最大应力为94.229 MPa,计算其刚度为3.179 6×107N/m,约为理论计算的2.5倍,需通过试验进一步验证。

图4 鼠笼弹支外圈变形云图

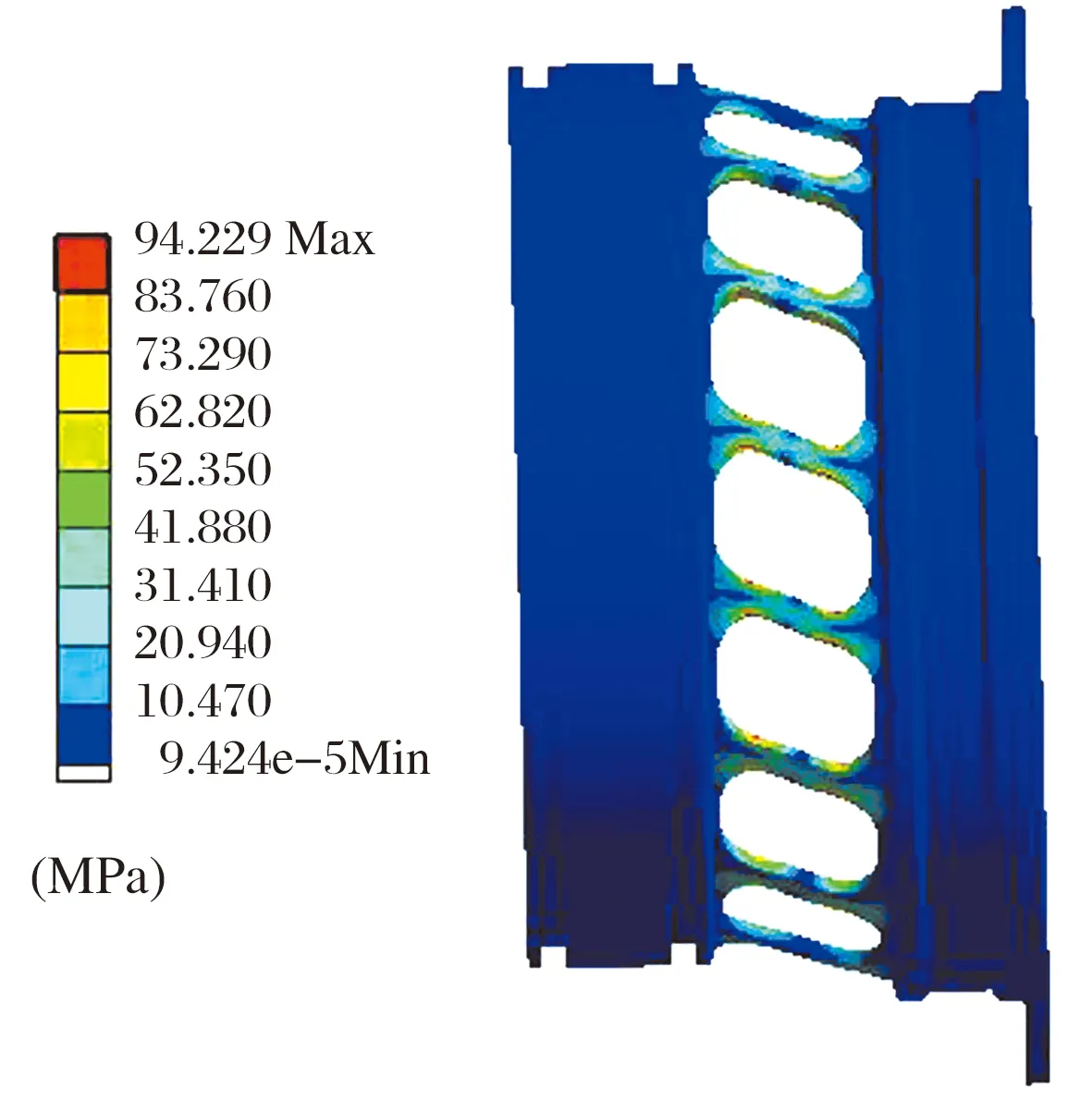
图5 鼠笼弹支外圈应力云图

鼠笼弹支外圈刚度测量示意图如图6所示,外圈一端固定在测量平台上,在外圈自由端沟道中心施加径向载荷,外圈刚度为径向载荷变化量与外圈自由端沿加载方向的位移变化量的比值。测量结果见表1,外圈刚度为3.21×107N/m,与有限元法误差为0.947%, 说明可以采用有限元法计算鼠笼弹支外圈刚度。产生误差的原因为端面安装位置自由度为0,实际螺栓固定时会有微小变形,且建模时未考虑外圈靠近凸缘的减重孔。

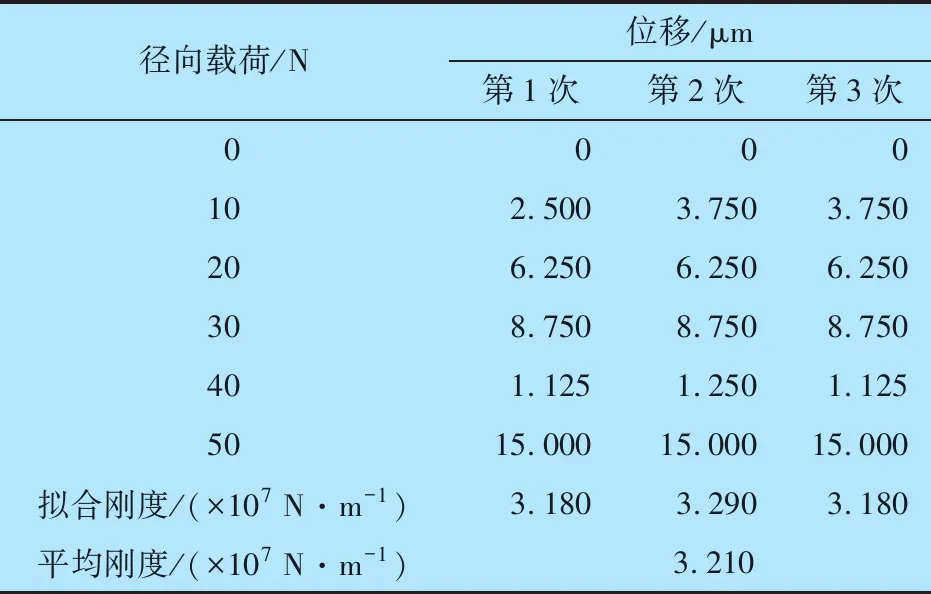
表1 鼠笼弹支外圈刚度测量结果

图6 鼠笼弹支外圈刚度测量示意图

3 鼠笼弹支外圈优化设计

基于ANSYS APDL建立鼠笼弹支外圈参数化分析模型,结合ANSYS Workbench的多变量优化设计方法[13-14],在材料强度允许范围内,以肋条厚度h、肋条宽度b、肋条数量N、肋条长度l和过渡圆角半径R为设计变量,以鼠笼肋条圆角处最大应力值最小为优化目标,以转子动力学临界转速对应的变形为约束,从而得到最优刚度[11-12]。

以某发动机鼠笼弹支轴承为例,其主要结构参数见表2,套圈材料泊松比为0.3,弹性模量为168 GPa。刚度要求为1.9×107～2.1×107N/m,在100 N的径向载荷作用下,外圈变形要求为4.760～5.263 μm。根据设计及加工经验,暂定设计变量初值及其变化范围见表3。进行迭代计算获得最优解,最优解附近的30组不同设计变量鼠笼弹支外圈变形如图7所示,鼠笼肋条圆角处的最大应力如图8所示,仅第3,8,13,23组满足变形要求,其中第3组最大应力值最小为17.87 MPa,变形为4.873 μm,刚度为2.052 1×107N/m,满足要求。则优化设计结果为:h=2.8 mm,b=2.8 mm,N=14,l=22 mm,R=4 mm。

表2 鼠笼弹支轴承主要结构参数

表3 鼠笼弹支外圈设计变量初值及其变化范围

图7 不同设计变量鼠笼弹支外圈的变形

图8 不同设计变量鼠笼肋条圆角处的最大应力

4 鼠笼弹支轴承性能分析

4.1 有限元模型

鼠笼弹支轴承凸缘通过螺母固定在承力框架上,未考虑内、外圈柔性时,将外圈和箱体集成为一体,基于Romax建立鼠笼弹支轴承分析模型,如图9a所示。考虑柔性时,将优化设计的鼠笼弹支外圈有限元模型存成.cdb格式导入Romax,内圈、轴柔性化处理,模型将完整呈现弹支结构,由于内、外圈有限元化,球需要重新与其进行节点连接并进行缩聚,如图9b所示。

(a) 未考虑柔性 (b) 考虑柔性

对轴承施加377 N的径向载荷,355 N的轴向载荷,转速为33 750 r/min。由于考虑套圈柔性时不能考虑温度对游隙及寿命的影响,为便于对比分析,假设两模型温度为20 ℃,两模型的径向工作游隙与常规计算的径向工作游隙相同。

4.2 刚度计算

考虑柔性时轴承套圈变形如图10所示,鼠笼弹支外圈最大变形为17.7 μm,内圈最大变形为253.39 μm,计算鼠笼弹支外圈刚度为2.13×107N/m,与优化设计结果接近。

(a) 鼠笼弹支外圈

4.3 载荷分布及寿命计算

未考虑和考虑柔性时轴承载荷分布对比见表4,考虑柔性时轴承承载球数多,球承受的最大载荷小,内、外圈接触应力小。

表4 未考虑和考虑柔性时轴承载荷分布对比

未考虑和考虑柔性时轴承载荷分布如图11所示。

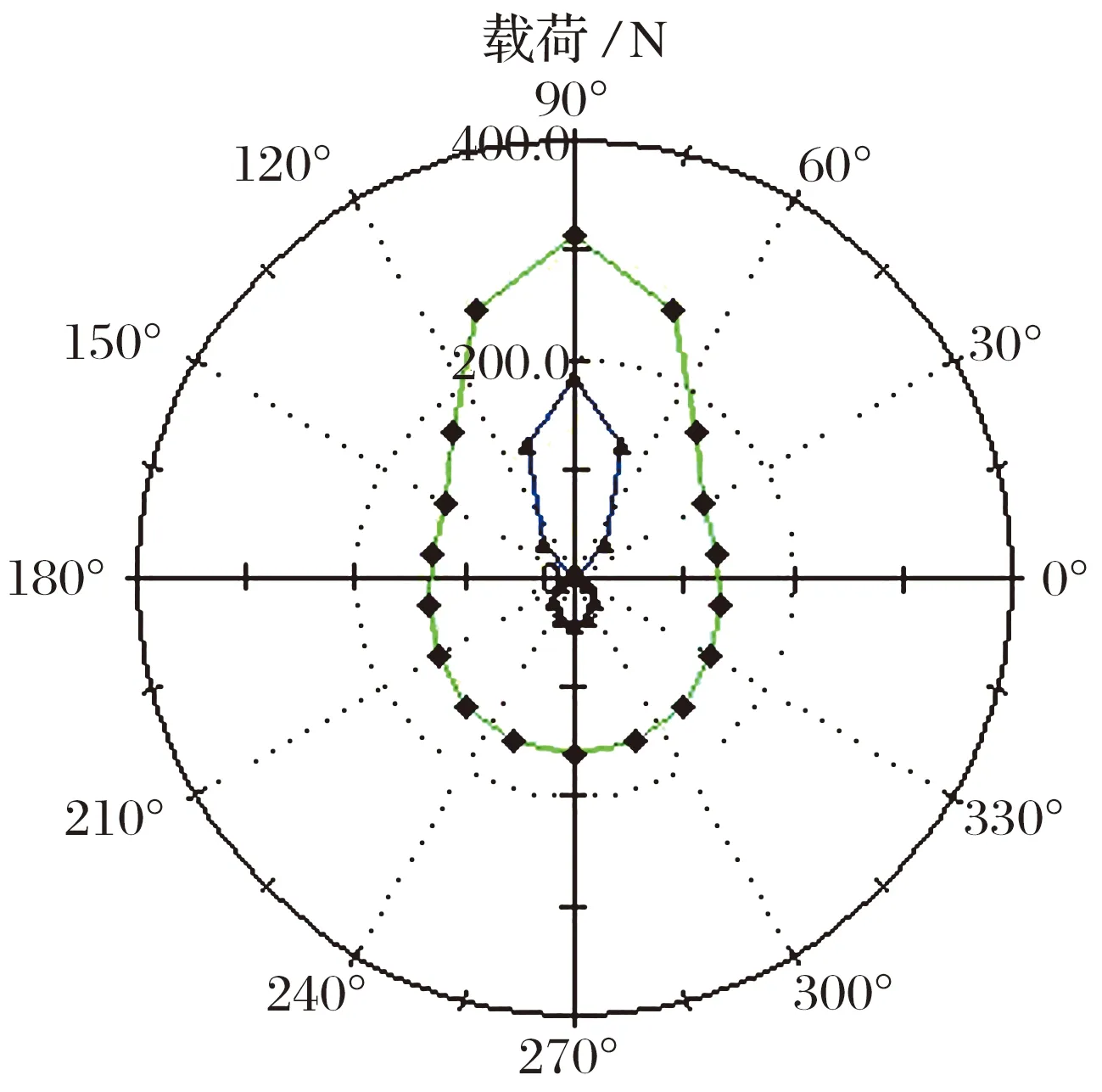
图11 未考虑和考虑柔性时鼠笼弹支轴承的载荷分布

考虑柔性时轴承整体寿命不等于内、外圈预测寿命最小值,应根据轴承实际载荷[15-18]分布先计算内、外圈额定寿命,再计算整套轴承寿命,即

(2)

Li=(Qc/Qei)3,

Le=(Qc/Qee)3,

式中:Li,Le分别为内、外圈额定寿命;Qc为轴承基本额定动载荷;Qei,Qee分别为内、外圈当量载荷。

轴承内圈固定,外圈旋转,则内、外圈当量载荷分别为

(3)

(4)

式中:Z为球数;Qi,Qe分别球与内、外圈的接触载荷。

对于接触角小于45°的向心球轴承,其基本额定动载荷为

(5)

式中:f为轴承沟曲率半径系数;α为接触角;γ为与接触角有关的参数;Dw为球直径。

考虑柔性和不考虑柔性时轴承寿命分别为2.862 9×105,2.543 2×105h,考虑柔性时轴承载荷分布更均匀,寿命更长。

5 结束语

建立某鼠笼弹支轴承外圈有限元模型对其刚度进行计算,考虑笼条过渡圆角对鼠笼弹支外圈进行优化设计,并提出该类轴承性能分析时应考虑鼠笼弹支外圈柔性的影响,分析结果可为该类轴承的设计和应用提供参考。但本文主要对鼠笼弹支轴承外圈进行了优化设计,缺少整套轴承的优化设计,后续有待进一步研究。