含轴向裂纹X80 压力管道弹塑性断裂分析
宋琦SONG Qi;姚钧宇 YAO Jun-yu;彭惠芬 PENG Hui-fen
(①卡迪夫大学工程学院,卡迪夫CF24 3AA UK;②东北石油大学机械科学与工程学院,大庆 163318)
0 引言
随着压力输送管道建设的迅猛发展,长输距、大管径、高压力管道是当今世界压力管道发展的总趋势。由于管道在制造、安装或服役过程中不可避免产生微裂纹,这些微裂纹在长期载荷作用下引起断裂的事故时有发生,给国民经济造成了巨大的损失[1-3]。如何正确评定含裂纹压力管道的安全可靠性是目前国内外科技工作者关注的焦点[4-5]。应力强度因子是在裂尖小范围屈服条件下对含裂纹压力管道进行安全性评定的一个重要参数,许多学者开展了相关方面的研究。白永强等[6]基于输气管道裂纹动态数值模型,研究了管道壁厚、止裂长度及管道内压对裂纹动态扩展的影响;姚安林等[7]基于虚拟裂纹闭合技术,利用大型有限元分析软件ANSYS 对含多条半椭圆裂纹高压输气管道的应力强度因子进行计算;王爱勤[8]基于权函数方法研究了含轴向裂纹海洋管道应力强度因子积分实用计算公式,为海底管道断裂参数计算提供了参考依据;陈旻炜等[9]为避免裂纹尖端网格划分缺陷,基于相互作用积分方法分析了带孔板裂X100 管线钢二维和三维裂纹的弹塑性约束失效规律;苗婷等[10]运用界面单元CZM 研究了X65 管线钢裂纹扩展问题并与试验结果进行对比,优化了有限元模型;王钟羡等[11]在J-Q 双参数理论基础上,考虑裂尖塑性效应,通过匹配标准裂纹试件和管道J-Q 有限元计算结果得到它们约束效应的相关性,进而对X80 管线钢裂纹体进行了弹塑性断裂分析;黄建业[12]基于弹塑性断裂力学数值计算方法,分析了轴向直裂纹X100 管线钢二维和三维裂纹约束失效机理;柳军等[13]采用耦合有限元-无网格Galerkin 法,研究了碳纤维缠绕修复压力管道横向表面椭圆型裂纹应力强度因子,对管道修复提供了有益参考。
上述对于含裂纹管道断裂分析问题主要从计算方法及能量角度对管道进行断裂分析,提高了数值计算精度,实现了裂纹动态扩展的模拟。由于管道裂纹尖端应力以r-1/2阶次趋于无穷大,高压薄壁管道在无穷大应力作用下裂尖必然屈服,管道柔度增大,将等效有更多裂纹产生[14],此时裂尖塑性尺寸将给断裂分析带来很大误差。为此,笔者利用ANSYS APDL 自编译程序,采用弹塑性材料模型,对含轴向穿透裂纹压管道进行断裂分析,依据Von Mises屈服准则,确定塑性影响区域,基于相互作用积分法计算应力强度因子,分析了含轴向裂纹压力管道弹塑性极限载荷及塑性修正后应力强度因子随管道半径、壁厚的变化规律,给出了不同压力下应力强度因子塑性修正相对误差,为现役含裂纹高压力管道安全评估提供一定的参考依据。
1 小范围屈服应力强度因子塑性修正
裂纹尖端小范围屈服,即当r→0,裂纹尖端附近的应力以r-1/2的阶次趋于无穷大,在趋于无穷大应力作用下材料必然要发生屈服。管道轴向裂纹主要是I 型裂纹,假设管道无限长,径厚比大于10,可视为薄壁压力管道平面应变问题。讨论其裂纹尖端的屈服尺寸,根据Von Mises 屈服准则,估计裂纹尖端屈服尺寸,在裂纹延长线上(即θ=0),应力强度因子KI。
式中,β1为几何修正因子;σθ为管道环向应力;a 为裂纹初始长度;P 为管道压力;R 为管道半径;t 为管道厚度。
平面应变下薄壁管道裂纹尖端应力场可表示为:
式中,σθ、σz、σr分别为管道环向、轴向和径向应力,τrθ、τrz、τzθ三个面剪切应力为管道材料泊松比。
根据Von Mises 屈服准则,管道裂纹尖端屈服尺寸应为:
式中,σs为管道的屈服强度。
依据Irwin 塑性修正后的应力强度因子:
在裂纹延长线上(θ=0)上,应力σθ为
将rp代入式(6),则修正后的应力强度因子
2 数值分析模型的建立及验证
2.1 数值模型的建立
本文研究含轴向穿透裂纹压力管道I 型裂纹,针对X80 管线钢,管道几何尺寸:管道内径R=610mm,壁厚t=18mm,管道长度l=4000mm,初始裂纹长度a=15mm,裂纹深度w=18mm;采用理想弹塑性模型,材料参数:弹性模量E=2.03×1011Pa,屈服应力σs=560MPa,泊松比μ=0.25,Ramberg-Osgood 应力—应变关系:,其中,硬化指数n=13,材料常数λ=1.07。
运用ANSYS 软件自编译程序APDL,建立含轴向穿透裂纹压力管道三维弹塑性有限元模型。假设管道无限长,可看作平面应变问题,整个管道在以中心裂纹为基点的环向和轴向具有对称性,选取整体模型的1/4 作为计算模型,采用SHELL281 单元划分网格,将8 结点的SHELL281 单元边中结点移至单元边长1/4 处,使其在邻边角节点处的应力场在单元内具有奇异性,为S HELL281 等参奇异元。在裂纹尖端建立局部坐标系,利用ANSYS 软件KSCON 命令,将整个管道模型单元沿厚度方向划分为8 层,裂尖网格模型如图1 所示。边界条件为:管道左、右端面及与裂纹平面平行的无裂纹一侧切平面为对称约束,与裂纹平面平行的有裂纹一侧切平面不添加约束(图2),管道内表面施加压力。基于上述有限元模型,利用裂尖局部坐标系,采用相互作用积分法对含轴向穿透裂纹压力管道进行弹塑性断裂分析。

图1 管道裂纹尖端奇异元

图2 管道约束方式
2.2 数值模型的验证
表1 列出了管道内压为8MPa,不同裂纹初始长度下含轴向穿透裂纹压力管道应力强度因子KI数值模拟结果与《应力强度因子手册》[15]计算结果的相对误差。由表1 可知,管道应力强度因子KI随裂纹初始长度的增加而增加,数值解与《应力强度因子手册》计算结果的相对误差随着裂纹初始长度的增加而增大,a=60mm 时最大相对误差为8.60%,表明该有限元模型的求解是可靠的。
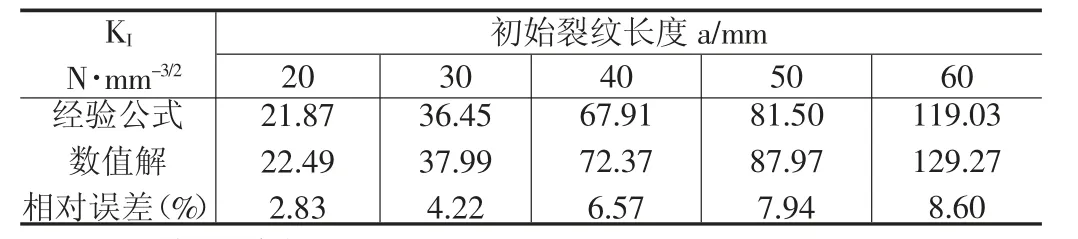
表1 KI 误差分析表
3 结果分析
3.1 含轴向裂纹管道弹塑性分析
设含轴向穿透裂纹压力管道裂纹尖端应力刚开始屈服时,所对应的压力为含轴向穿透裂纹管道弹性极限载荷Pe;随着管道内压的增加,当管道裂纹所在截面上的净截面应力达到屈服应力时,塑性区将扩展至整个截面,造成全面屈服,此时所对应的压力为塑性极限载荷Pl[16-17]。基于含轴向穿透裂纹压力管道三维弹塑性有限元模型,获得了含轴向穿透裂纹压力管道弹、塑性极限载荷见表2。

表2 裂纹初始长度与弹塑性极限载荷及初始屈服时间关系
从表2 中可看出,管道几何参数、材料参数确定后,管道弹塑性极限载荷随裂纹初始长度增加而减小,裂尖初始屈服所需时间随管道裂纹初始长度增大而逐渐减小。
3.2 应力强度因子塑性修正
表3 列出了管道内压一定,不同初始裂纹长度下,含轴向穿透裂纹压力管道应力强度因子塑性修正前后相对误差与初始裂纹长度关系。由表3 可知,KI塑性修正前后相对误差随初始裂纹长度的增加非线性急剧增大,当a=60mm,P=8MPa 时,KI塑性修正前后的最大相对误差为8.60%,显然,塑性修正前断裂参数将不能准确评估管道安全性。

表3 KI 塑性修正前后相对误差分析表
3.3 管道几何参数对修正后应力强度因子的影响
图3 为管道t、l 一定时,不同管道R 下塑性修正后应力强度因子KI随裂纹初始长度a 的变化规律。由图3 可以看出,管道t、l 一定时,塑性修正后KI随管道半径R 的增大有小幅度的增加,同一管道R 下,塑性修正后KI随裂纹初始长度a 的增长而增大。
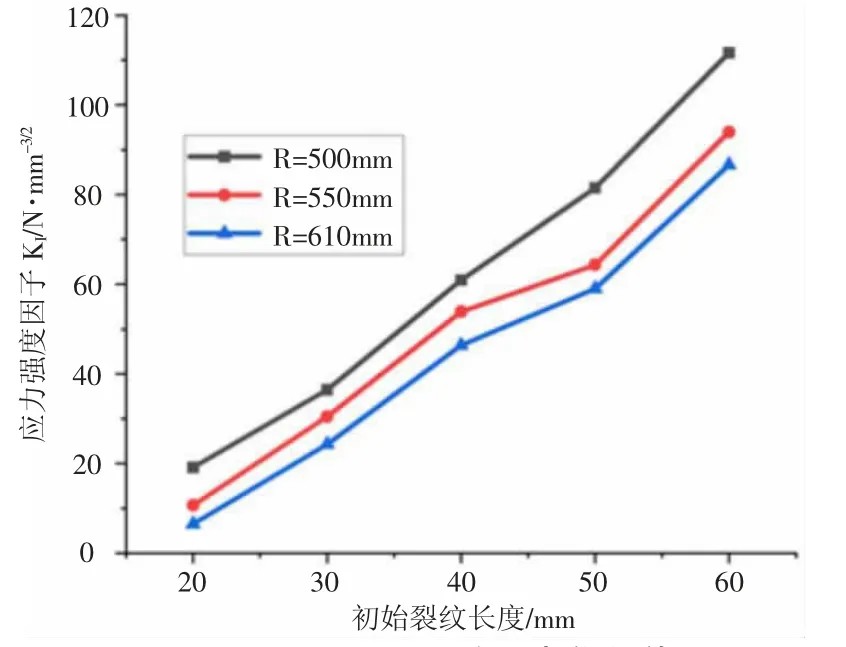
图3 不同R 下KI 随a 变化规律
图4为管道R、l 一定时,不同管道t 下塑性修正KI随裂纹初始长度a 的变化规律。由图4 可以看出,管道R、l一定时,塑性修正后KI随管道厚度t 的增加而减小,同一管道t 下,KI随a 的增加而增大。
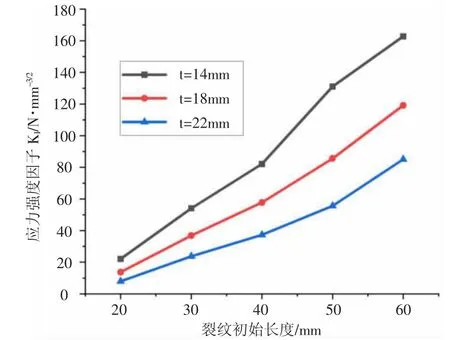
图4 不同t 下KI 随a 变化规律
4 结论
利用ANSYS APDL 自编译程序建立了含轴向穿透裂纹压力管道三维有限元弹塑性分析模型,基于相互作用积分计算裂纹尖端断裂参数,分析了裂尖塑性区应力-应变分布规律及应力强度因子塑性修正前后相对误差,得到如下结论:①含轴向穿透裂纹压力管道弹塑性极限载荷仅是管道几何、材料参数及裂纹初始长度的函数,上述参数确定,管道弹塑性极限载荷为恒定值;在管道几何尺寸及材料参数确定下,含轴向穿透裂纹管道弹塑性极限载荷随管道裂纹初始长度的增加而减小。②材料屈服强度不变条件下,应力强度因子塑性修正前后误差随着管道内压增大而增大,当管道内压为8MPa 时,应力强度因子塑性修正前后相对误差已达8.60%,此时忽略裂尖塑性区影响,将使管道安全评定产生较大误差。③塑性修正后管道应力强度因子KI随管道半径R 的增加而增大,随管道厚度t 的增加而减小,随初始裂纹长度a 的增加呈非线性增加。

