基于AHP-CIM 模型的全过程工程咨询质量评价
——以甘肃省建筑设计研究院有限公司为例
田文娟 TIAN Wen-juan
(甘肃省建筑设计研究院有限公司,兰州 730000)
0 引言
近些年来,随着我国工程建设行业的迅速发展,对工程咨询企业的咨询服务质量也提出了更高的要求和挑战,一般的工程咨询服务由于业务零碎,过程繁琐,已经很难适应当前工程建设市场的需求。基于此种情况,全过程的工程咨询服务体系应运而生,全过程的工程咨询是指从项目前期的投资决策阶段,到项目后期竣工验收以及投入使用,涵盖项目的全生命周期,目的在于为客户提供综合的、高效的决策和指导,以此最大化项目的收益。然而,目前我国的工程咨询企业种类繁多,全过程工程咨询的服务质量得不到保障,所以,全过程工程咨询服务的质量评价就显得尤为重要。
罗岚等[1]通过整理全过程工程咨询中现有的问题,确定了六个影响全过程工程咨询服务质量的因素,并构建FCM 模型对六个因素进行分析,最后根据实际情况,对全过程工程咨询服务质量的改善和提升给出了相应的策略和意见;赵振宇等[2]通过构建全过程的工程咨询管理体系,对主要的内容进行探讨,并给出了相关的建议,具有一定的实践价值;任泽等[3]通过分析目前工程咨询企业存在的不足,提出了五种企业需要建设的能力,并从这五个方面出发,给出了提升工程咨询企业服务质量的策略;徐友全等[4]通过检索文献、走访专家的方式确定了22 项阻碍全过程工程咨询实施的因素,并运用ISM 的方法对因素间的关联关系进行分析,最后给出了相应的意见;张国兴等[5]通过对工程实践和相关文献的研究,提出了三种工程咨询的组织模式,具有一定的参考价值;Deng Chunyao[6]总结了全过程工程咨询管理研究的重要性,并分析了我国全过程工程咨询管理研究的优势和意义,最后提出了全过程工程咨询服务在建设项目中的应用和对策。
通过上述文献总结,可以发现全过程工程咨询质量评价对于建设工程的重要性和意义,然而,目前全过程工程咨询质量评价相关研究还较少,基于此,本文提出了基于AHP-CIM 模型的全过程工程咨询质量评价体系,通过检索文献,确定了与全过程工程咨询质量评价相关的因素,并结合实际案例进行了分析和探讨,对工程咨询企业的全过程工程咨询质量评价具有一定的借鉴和参考价值。
1 全过程工程咨询质量评价体系
通过检索和筛选与全过程工程咨询相关的文献,确定评价指标,构建评价体系。本文选取了6 篇与全过程工程咨询相关的文献,从中确定了4 个一级指标,分别为:运行体系、业务水平、成果质量和基本条件,以及13 个二级指标。通过层次分析法(AHP)确定指标权重,可以直观地反应各指标间的重要性,为全过程工程咨询的质量评价提供依据,详情见表1。
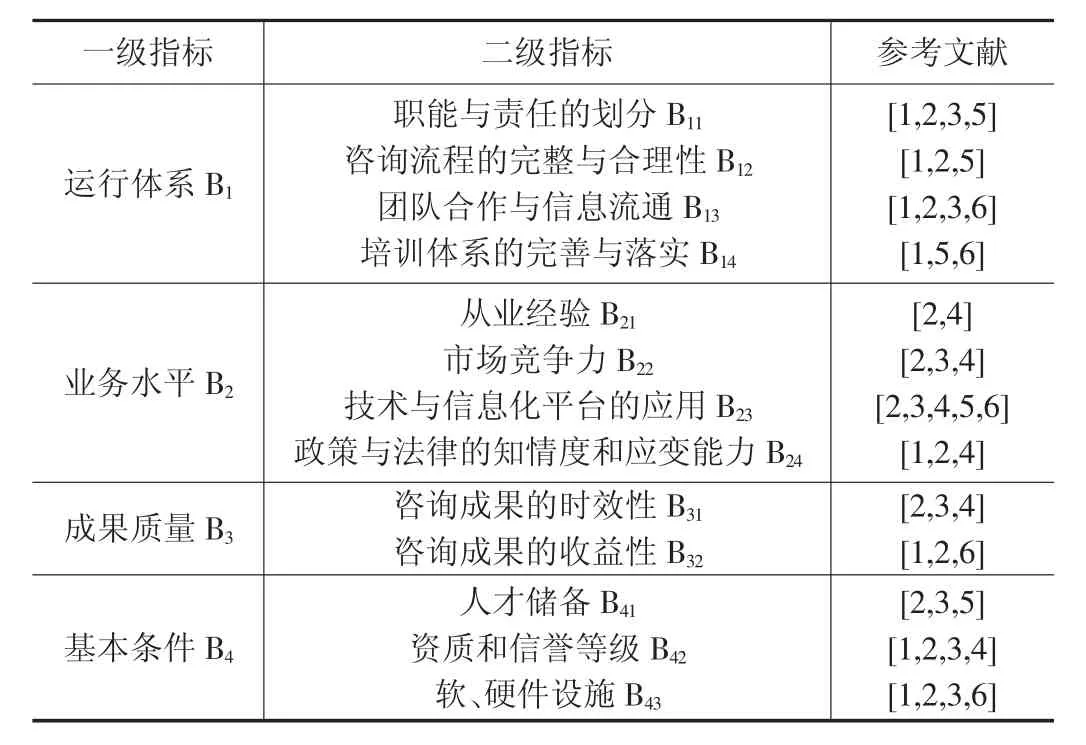
表1 全过程工程咨询质量评价体系
2 基于AHP-CIM 模型的全过程工程咨询质量评价体系
2.1 层次分析法(AHP)
在20 世纪70 年代,美国学者托马斯·L·塞蒂(Thomas L. Saaty)提出了层次分析法的概念[7],是质量评价中常用的一种方法,通过将定性的问题转化为定量的数据,使得复杂的问题简单化,具体步骤如下:
①构造判断矩阵。
邀请工程咨询行业内的专家分别对各指标两两之间进行比较打分,得到判定矩阵A,并求A 中每行元素的乘积。
式中,aij为第i 个因素对第j 个因素的相对重要性得分,它满足以下条件:
在判断矩阵A 中数字的含义见表2。

表2 数字标度含义
②计算指标权重。
将矩阵A 乘以权重,得到矩阵AW。
③求最大特征值。
式中,wi为第i 个指标的权重,(AW)i为AW 的第i 个分量。
④一致性检验。
式中,CI 为一致性指标值,n 为判断矩阵阶数。
式中,CR 为随机一致性比值,若CR 小于0.1,则表示一致性检验通过,反之不通过,对通过一致性检验的结果求平均值,即可得到最终的权重结果。RI 为平均随机一致性指标值,其取值与矩阵阶数n 有关,详情见表3。

表3 平均随机一致性指标的取值
2.2 控制区间与记忆模型(CIM)
控制区间记忆模型(Controlled Interval and Memory Models)最早起源于经济学中[8],近年来,AHP-CIM 模型常用于质量和风险评价当中。本文以甘肃省建筑设计研究院有限公司为研究对象,通过AHP-CIM 模型对其全过程工程咨询质量进行评价,采用层次分析法(AHP)从纵向层面确定各指标的权重,再利用控制区间与记忆模型(CIM)从横向逐层分析各指标的质量评级的概率,最后将指标权重与质量评级的概率相乘,即可确定研究对象最终的全过程工程咨询的质量评级,具体流程见图1。

图1 质量评价流程
CIM 模型的计算思路就是将前一个指标的计算结果与后一个指标的计算结果叠加,直至将该指标层的全部指标叠加完毕,即可确定该指标层的质量评级概率,具体步骤如下:①建立质量等级评语集。建立评语集V={优秀,良好,一般,较差,很差},并设立质量等级对应的数值(5,4,3,2,1),以便于更直观地体现质量等级,邀请行业内的专家对二级指标的质量等级进行打分,得到初始数据。②数据统计和处理。二级指标的质量等级的概率满足以下公式:
式中,N 为专家总人数,Nj为指标在某一等级下的专家打分人数。
2.3 利用并联响应模型计算一级指标质量等级的概率,公式如下:
式中,X1、X2为不同的质量指标,xa为划分的质量等级。
3 实例分析
3.1 指标权重的计算
这里以一级指标为例,邀请6 名工程咨询领域内的专家对指标进行比较打分,构造判断矩阵并求得权重,对通过一致性检验的结果统计并求平均值,即可得到各评价指标的最终权重,详情见表4。

表4 全过程工程咨询质量评价体系一级指标权重
3.2 AHP-CIM 模型的质量评价分析
以甘肃省建筑设计研究院有限公司为例,本文邀请10 名工程咨询领域内的专家通过质量评语集对该公司的全过程工程咨询质量的二级指标进行量化分析,得到二级指标质量评价的概率分布表,详情见表5。

表5 全过程工程咨询质量评价二级指标的概率分布——以甘肃省建筑设计研究院有限公司为例
横向考虑各质量评价指标的关联性和独立性,采用CIM 并联响应模型将同一个一级指标下的二级指标依次叠加,直至最底层。由于全部计算过程较为繁琐,本文仅列举了运行体系B1的计算过程,运行体系B1包含4 个二级指标,分别为:职能与责任的划分B11、咨询流程的完整与合理性B12、团队合作与信息流通B13以及培训体系的完善与落实B14。先将B11与B12并联叠加得到B112,再将B112与B13并联叠加得到B1123,最后将B1123与B14并联叠加即可得到最终运行体系B1的质量评级的概率,具体计算过程如下:
B11与B12叠加后得到B112的质量评级的概率为如下。
优秀的概率为:7/10*8/10=56/100
良好的概率为:2/10*(8/10+1/10)+1/10*7/10=25/100
一般的概率为:1/10*(8/10+1/10+1/10)+1/10*(7/10+2/10)=19/100
较差的概率为:0
很差的概率为:0
B112与B13叠加得到B1123的质量评级的概率如下。
优秀的概率为:56/100*7/10=392/1000
良好的概率为:25/100*(7/10+1/10)+1/10*56/100=256/1000
一般的概率为:19/100*(7/10+1/10+1/10)+1/10*(56/100+25/100)=252/1000
较差的概率为:1/10
很差的概率为:0
B1123与B14叠加得到最终B1的质量评级的概率如下。
优秀的概率为:392/1000*7/10=2744/10000
良好的概率为:256/1000*7/10=1792/10000
一般的概率为:252/1000* (7/10+2/10)+2/10*(392/1000+256/1000)=3564/10000
较差的概率为:1/10+1/10*(392/1000+256/1000+252/1000)=19/100
很差的概率为:0
同理可求得B2、B3和B4的质量评级的概率,详情见表6。
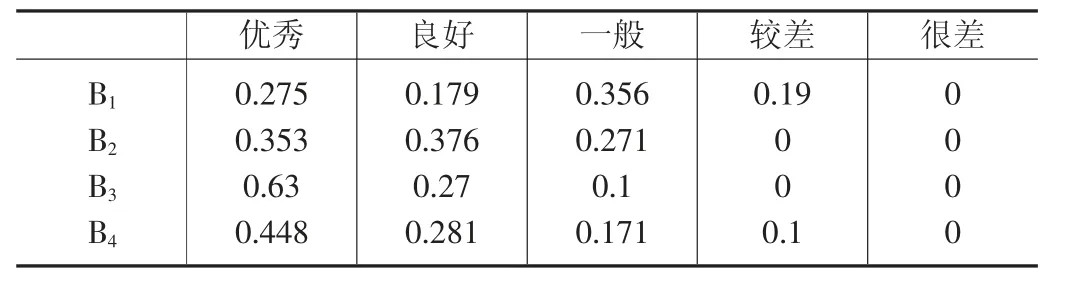
表6 全过程工程咨询质量评价一级指标的概率分布——以甘肃省建筑设计研究院有限公司为例
将表6 中质量等级的概率分布乘以一级指标的权重,即可求得甘肃省建筑设计研究院有限公司的全过程工程咨询质量等级的最终概率,详情见表7。

表7 全过程工程咨询质量评价等级概率——以甘肃省建筑设计研究院有限公司为例
将表7 中质量等级的概率乘以预设的质量等级对应的数值(5,4,3,2,1),即可直观地反映出甘肃省建筑设计研究院有限公司的全过程工程咨询质量评价等级。
由计算结果可知,甘肃省建筑设计研究院有限公司的全过程工程咨询质量评价等级处于“良好”和“优秀”之间,整体的工程咨询水平较高。
4 结语
考虑到全过程工程咨询质量评价的重要性以及目前相关研究较少的情况,本文通过阅读和筛选文献,构建了4 个一级指标:运行体系、业务水平、成果质量和基本条件以及13 个二级指标的全过程工程咨询质量评价体系,利用AHP-CIM 模型的方法分别确定了指标的权重和概率,并以甘肃省建筑设计研究院有限公司为例,对其全过程工程咨询质量等级进行了评价。根据AHP 计算求得的指标权重可以看出,业务水平所占比重最高,其次是运行体系和成功质量,最后是基本条件,所以咨询企业要重视自身的业务水平,多积累从业经验,提高自身的市场竞争力,紧跟时事,及时了解国家和地方的政策法律,提高企业自身应对风险的能力,当然其他方面也需要重视,例如:明确分工和职能,注重企业自身信誉和资质的建设,完善企业办公设施等等。从甘肃省建筑设计研究院有限公司的全过程工程咨询质量评价结果来看,该企业评价等级处于“良好”和“优秀”之间,整体水平较高,但也有一定提高和改善的空间。

