基于数值模拟的独头巷道热舒适性研究与优化

马 东 任 能 杨 欠

（安徽工业大学能源与环境学院）

随着矿井开采深度的增加，井内的热害现象愈加严重，尤其对于通风不畅的独头巷道更是如此。高温、高湿的巷道环境不仅影响了工人们的工作效率，还严重损害着人们的健康［1］。通风降温由于成本低廉且操作简便成为巷道的主要降温手段［2］。

对于独头巷道通风与优化方面，已有一些研究。王文才等［3］对风筒悬挂位置与通风效果之间的关系进行了研究，得出了风筒出口至掘进工作面距离的最佳公式，为送风风筒的布置提供了依据；杜翠凤等［4］对掘进巷道的通风降温进行模拟，得到了风流温度与风量、入风温度及岩壁温度的变化规律；曹亚平［5］分析得出风量与出口风温之间近似为幂函数关系；余学云等［6］基于PMV指标对巷道内的温湿环境进行研究，优化了送风速度及温度，在送风满足人体热舒适度的基础上提出了节能策略。目前大多数巷道的通风设计是参照《金属非金属矿山安全规程》［7］，要求井下作业地点温度达到26℃以下，但实际投入运行的通风系统较少考虑到人体舒适度，部分针对人体热舒适度的研究未考虑送风湿度对降温效果的影响。

通过Fluent软件对巷道内的风流流动进行数值模拟，分析送风风筒直径及送风参数对降温效果的影响。将工人工作区域视为舒适度控制区，引入PMV指标评价控制区的热环境并确立最优制冷方案。

1 热环境评价指标

对于矿井热环境的评价，可分为主观评价指标与客观评价指标。其中主观评价指标即采用问卷调查方式通过工人们的主观意识对矿井热环境进行评价。客观评价指标则包括空气龄、换气效率、能量利用系数、PMV-PPD等［8］。

PMV（Predicted Mean Vote）综合反映了稳态热环境下人的活动、衣着、环境的空气温度、相对湿度、风速与辐射温度等因素的关系及其综合影响，是表征人体热舒适的一个较客观的指标［9］。其计算公式为

式中，M为人体代谢率，W/m2；W为人体所作机械功，W/m2；Pa为空气中水蒸气分压力，pa；ta为人体周围空气温度，℃；tr为平均辐射温度，℃；fcl为服装面积系数，tcl为服装外表面温度，℃；hc为表面传热系数，W/（m2℃）。

PMV对应的热感觉等级划分见表1。

2 数值模拟

2.1 物理模型

模拟计算对象为深井独头巷道，其几何尺寸为12 m×2.6 m×2.8 m（长×宽×高）。风筒轴心距巷道顶端0.5 m，距巷道侧壁0.5 m。将几何尺寸为3 m×2.4 m×1.5 m（长×宽×高）的立方体区域作为舒适度控制区域并对其重点分析。控制区域距巷道掘进面0.3 m，距巷道底部0.3 m，距两侧壁面0.1 m（图1）。

2.2 数学模型

2.2.1 基本假设

巷道中风流呈高雷诺数的紊态流动，为简化问题，对风流做出合理假设如下：

（1）巷道内风流为三维稳态流体，流体的紊流黏性具有各向同性。

（2）巷道内风流为不可压缩流体且满足Boussinesq假设，即认为流体的密度变化仅对浮力产生影响。

（3）壁面为定温边界条件。

（4）忽略巷道内除围岩以外的其他散热及流体黏性力做功引起的耗散热。

2.2.2 控制方程

基于以上假设，巷道内风流的质量方程、能量方程、动量方程等采用通用形式：

式中，ρ为空气密度；ϕ为通用变量；V为速度矢量；Sϕ为源项；Γϕ为扩散项系数。

2.3 边界条件与参数设定

该物理模型以风筒出口为入口边界条件，以风筒出口处的巷道截面为出口边界条件。入口边界条件设为速度入口，出口边界条件设为自由出流，壁面条件设为无滑移边界条件，壁温30℃，巷道相对湿度85%。

2.4 研究案例

固定送风量6 104 m3/h，研究不同风筒直径、送风温度和相对湿度条件下的独头巷道内的温度、湿度、速度和PMV场的分布特性。案例情况见表2。

3 结果分析

3.1 风筒直径

为探究风筒直径对通风降温效果的影响，选取案例1～案例3并截取过风筒中心轴线垂直剖面进行分析。

过风筒中心轴线垂直剖面温度分布如图2所示，风流从送风风筒射出后形成低温区域。随着送风射流的发展，风流与巷道高温壁面之间发生对流换热，沿巷道轴向方向温度逐渐增大。沿巷道垂直方向，由于底部岩壁温度较高且距离低温风流较远，换热效果较差，因此巷道底部风流温度偏高。对比案例1～案例3可知，600 mm直径送风风筒的降温效果要优于其他2种风筒。

过风筒中心轴线垂直剖面风速分布如图3所示，巷道风流流场分为附壁射流区、冲击射流区、回流区、涡流区［11］。风流从送风风筒射出后，不断卷吸周围空气并得到发展，且在经过一段距离后形成贴附射流。在巷道末端，射流体开始析出气体。射流体到达掘进工作面后形成冲击射流，冲击射流受到掘进面限制后折返并形成回流。回流区的一部分气体由于射流体的卷吸作用进入射流区，另一部分气体排出巷道外。射流区与回流区的交界处为涡流区。射流轴心速度随着射流的发展逐渐降低。对比案例1～案例3可知，600 mm直径风筒边缘更接近巷道岩壁，贴附效果更明显。

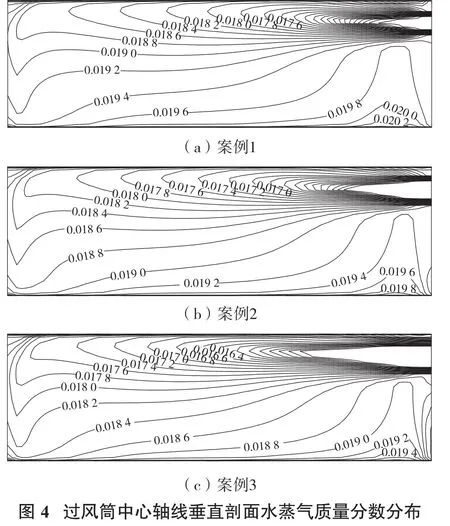
过风筒中心轴线垂直剖面水蒸气质量分数分布如图4所示，风筒出口射出的低湿风流与巷道内的高湿环境进行水蒸气交换后，高湿空气被带出巷道，进而巷道内水蒸气质量分数下降。随着风筒直径的增加，沿巷道垂直方向水蒸气分布梯度增大。对比图2与图4可知，巷道温度与水蒸气质量分数的分布具有相似性。

过风筒中心轴线垂直剖面PMV分布如图5所示，风流从风筒出口射出后PMV值不断升高。PMV值最高处为射流区与回流区交界处的涡流区，这是由于涡流区风速较低，无法带出热量。结合温度场分布来看，PMV和温度关系密切。温度越高的区域，PMV值越大。对比案例1～案例3可知，在相同位置，600 mm直径送风风筒下的PMV值相对其他2种风筒更低。

3.2 送风参数

为探究送风温度对通风降温效果的影响，选取案例4并截取过风筒中心轴线垂直截面Y=2.1 m进行分析，结果如图6所示。

送风温度降低而湿度不变时，通过图6（a）与图2（c）对比表明：相同位置的气流温度随之降低，巷道垂直方向上的温度梯度变大。通过图6（c）与图5（c）对比表明：PMV场受到温度及湿度变化的影响，相同位置处的PMV下降明显。

为探究送风湿度对通风降温效果的影响，选取案例5并截取过风筒中心轴线垂直截面Y=2.1 m进行分析，结果如图7所示。

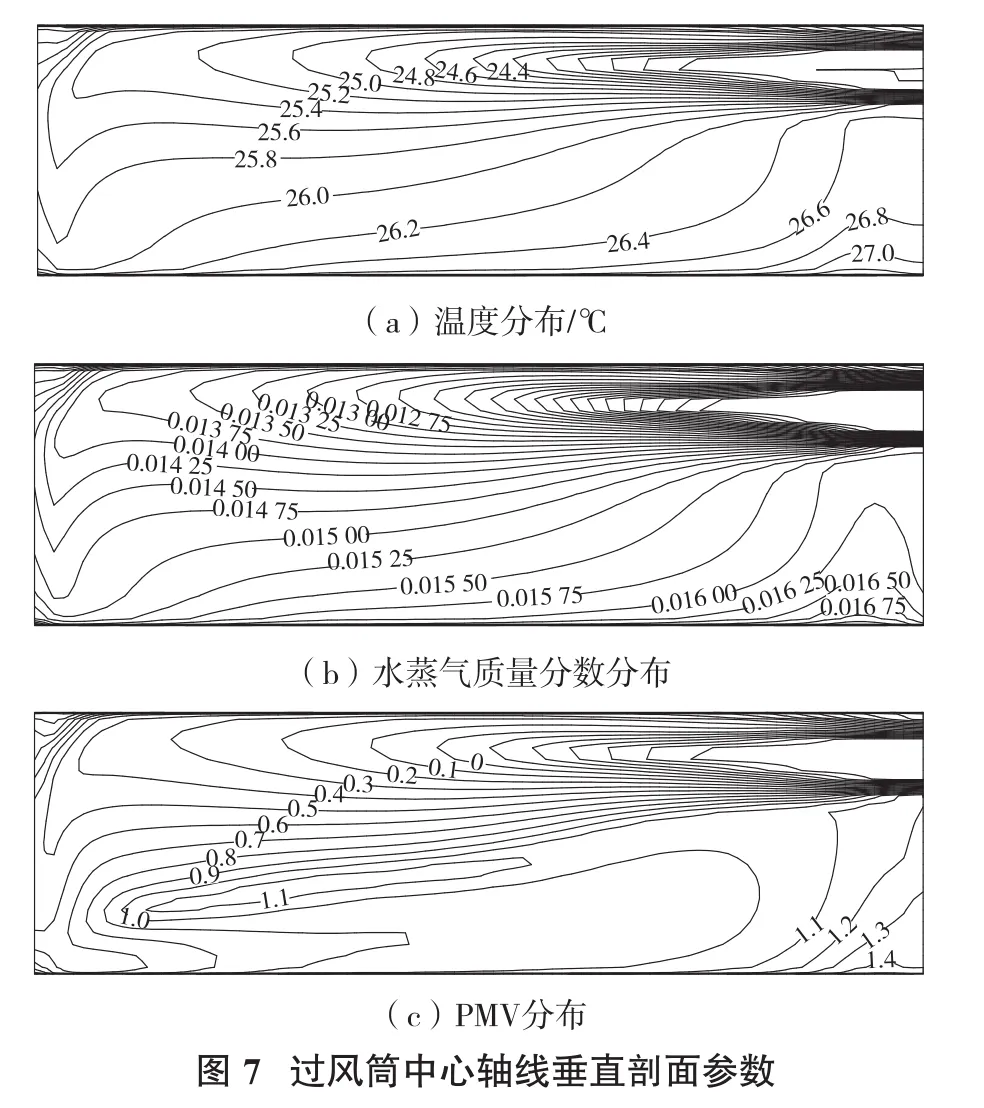
通过图6与图7对比表明，当送风湿度降低而温度不变时，由于风流与壁面的湿度差增大，巷道的湿度分布发生了变化，沿巷道垂直方向的湿度梯度增大。受到湿度变化的影响，相同位置处的PMV下降，但下降幅度较小。

4 制冷方案优化

沿垂直方向每隔0.3 m将控制区域切割为共6个平面，记录各平面上的最大与最小PMV值，整理并得到图8所示PMV散点图。

由图8可知，不同案例下控制区域PMV分布的趋势近似。案例1控制区域的PMV范围为1.24～1.73；案例2控制区域的PMV范围为1.19～1.70；案例3控制区域的PMV范围为1.12～1.66；案例4控制区域的PMV范围为0.53～1.26；案例5控制区域的PMV范围为0.46～1.18；案例6控制区域的PMV范围为-0.07～0.86；案例7控制区域的PMV范围为-0.16～0.80。由案例1～案例3的PMV分布可知：随着风筒直径的增加，控制区域内PMV整体下降。综上，较大直径风筒和较低风速的通风方式更适合独头巷道降温。平面1的PMV分布较低，这是因为平面1靠近巷道顶端，与低温送风风流接近，温度较低。平面4与平面5的PMV分布较高，这是因为平面4与平面5靠近巷道底部涡流区，风速较低且温度较高。

根据PMV对应热感觉等级可知：案例1～案例3下的控制区域最大PMV值均大于1，级别在Ⅴ（稍暖）—Ⅵ（暖），不满足舒适度控制需求。降低送风风流温湿度后，控制区域的PMV值随之降低，且温度变化对PMV影响更大。在案例6及案例7条件下，控制区域内PMV分布范围在-1～1，热舒适度评价为Ⅲ（稍凉）—Ⅴ（稍暖），基本满足舒适度控制需求。

各案例所需制冷量可按式（3）计算：

式中，Q为制冷量，kW；G为送风质量流量，kg/s；hw为巷道内风流焓值，kJ/kg；ho为送风风流焓值，kJ/kg。

由此得出各案例制冷量如图9所示。

由图8～图9可知，案例1～案例4的制冷量较低，不能满足巷道降温需求。案例5不仅不满足降温需求，且制冷量较高。而案例6、7可以满足巷道降温需求。比较案例6、7制冷量大小可知：案例6是巷道壁面温度30℃，相对湿度85%条件下的最佳制冷方案。

5 结论

（1）独头巷道压入式通风的风流流场分为贴附射流区、冲击射流区、回流区和涡流区。随着射流的发展，其贴附过程逐渐明显；风流从风筒出口流出后，经过与高温巷道岩壁的对流换热，其温度不断升高并在巷道末端趋于稳定；巷道风流的温度分布与水蒸气质量分数分布具有相似性。

（2）对于控制区域热舒适度而言，大直径风筒低风速条件下的PMV值更低；降低送风温度与相对湿度都会导致控制区域PMV值的下降，且温度改变对PMV的影响更大。因此综合送风所需的制冷量考虑，应采用较低温度较高相对湿度的送风风流。

（3）针对本文的独头巷道条件给出最佳方案：壁面温度30℃，相对湿度85%条件下，采取600 mm直径风筒通入v=6 m/s、t=20℃、相对湿度70%的送风风流。