基于改进分段Knothe函数的山区开采地表沉陷动态预计模型*
张力杰 盛 平 郑 诚
(1.山东能源集团有限公司;2.中国矿业大学力学与土木工程学院;3.杭州杭港地铁有限公司)
据统计,国内大型生产矿井“三下”压煤量接近138亿t,各矿区建筑物下压煤问题极其严重[1]。我国山西、重庆、云南等地不少矿区地貌为山地、丘陵地,受地形地貌影响,采动引起的坡体滑移、地表裂缝等灾害对地表建筑物有着较强的破坏性影响。对建筑物进行维修、及时释放采动变形引起的附加应力、控制地下开采对建筑物的破坏程度,是建筑物下压煤开采的重要技术途径。地表沉陷预测,尤其是动态沉陷预测是建筑物维修、加固方案设计的重要前提。
我国地表沉陷预测常见的方法包括典型曲线法、影响函数法、数值计算方法等,目前基本形成了以概率积分法为主体,多种沉陷预测方法共同发展的局面。总体而言,针对平原地区下煤层开采的地表沉陷的动态、静态预计都较为成熟,基于概率积分法与动态时间函数相结合的沉陷预测方法在各矿区获得了广泛应用[2-3]。山区地表沉陷预测目前主要采用《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》中推荐的山区地表沉陷模型,模型能够较好预测山区开采地表静态沉陷情况。山区开采沉陷动态预测仍缺少有效的方法。
为了实现较高精度的山区开采沉陷动态预计效果,本文在山区开采沉陷滑移模型的基础上,采用理论研究和实测研究相结合的方法,首先评估传统Knothe函数进行开采沉陷动态预测的效果;在此基础上,采用分段函数方法对Knothe函数进行改进,以达到工程精度需求。
1 山区开采沉陷动态预计理论
1.1 山区开采沉陷滑移模型
地形地貌产生的附加滑移是山区地表移动与变形相对平原区域不同的主要原因。何万龙[4]根据实测数据分析,求解各观测点的滑移分量以及变形值,分析总结山区复杂地形地质条件下工作面开采引起的变形分布规律,提出山区地表移动叠加原理。
依据山区地表移动叠加原理,山区地表下工作面开采任意点的下沉值,等价于相同地质条件平地下任意点的下沉值与采动滑移垂直分量的叠加,该任意点的水平移动值等价于相同地质条件平地下水平移动值与采动滑移水平分量的叠加。山区地表下任意点下沉值W'(x)和水平移动值U'(x)的预计公式为
式中,W'(x)和U'(x)分别为山区地形下工作面开采引起的地表点下沉值与水平移动值,W(x)和U(x)分别为相同地质条件下平地地形下工作面开采引起的地表点下沉值与水平移动值,ΔW(x)和ΔU(x)分别为受地形影响引起的滑移下沉与水平移动分量。
1.2 山区开采动态下沉过程
以工作面走向主断面为例,通常动态预计区间的划分取决于工作面开采长度或开采单元的回采时间,若将开始时刻t=0定于开切眼处开采时,第1个开采单元的开采时间为t1,其开采速度定义为v1,则第一个开采单元的单元长度为v1t1,同理若将第n个开采单元的开采时间定义为tn,开采速度为vn,则其开采单元长度为vntn。t时刻当n个开采单元开采后,地表某点的动态移动变形由每个单元开采造成的动态移动变形值叠加而成[5]。
第1个开采单元引起的地表下沉计算公式为
第2个开采单元引起的地表下沉计算公式为
则第n个开采单元引起的地表下沉计算公式为
式中,W'i表示山区地形下第i个单元开采引起地表某一点的稳态下沉。假设每个开采单元的开采时间相同,则可推导出山区开采地表动态移动与变形公式。
山区地形下工作面开采引起的地表动态下沉为
式中,W(xi-1)-W(xi)为相同地质采矿条件平地下工作面第i个单元开采引起的地表下沉值,mm;Dx为山区采动滑移系数;α为地表趋势面倾角;P(xi)为滑移函数;n为t开采时刻的单元个数。
山区地形下工作面开采引起的地表动态水平移动值为
式中,U(xi-1)-U(xi)为相同地质采矿条件平地下工作面第i个单元开采引起的地表水平移动值,mm。
2 时间函数的选取
现有的各类时间函数基本能够描述地表的实际动态下沉过程,其中Sroka-Schober时间函数实现的下沉速度变化趋势与现有下沉理论相符合,但该函数的下沉速度变化曲线高度不对称,导致整个地表下沉过程中的预计效果并不理想。广义时间函数增加了一个参数A,提高了函数适应性,但其函数图像不能较好地符合现有下沉理论。Logistic增长模型时间函数描述的地表下沉、下沉速度和加速度与实际情况相符,但其模型参数缺乏明确的物理意义。上述时间函数具有各自的优缺点,难以直接选取适当的时间函数,因此本文针对应用最为广泛的Knothe时间函数着手进行分析研究。
2.1 Knothe时间函数的分析
波兰学者Knothe在1952年提出了Knothe时间函数,假设某一时刻的地表下沉速度与地表最终的静态下沉值W0和t时刻的动态下沉值W(t)之差成比例[6-7]:
式中,t为预计时刻到工作面开挖时刻的时间长度;W(t)为t时刻地表动态下沉值,W0-W(t)为t时刻到地表沉陷稳定后的潜在下沉量,c为模型参数,也称时间常数,它的取值与采空区上覆岩层的物理力学性质密切相关。
根据初始时刻开釆边界条件:t=0,W(t)=0,对式(7)进行积分,可推导出
上述公式是Knothe时间函数计算地表动态下沉的表达式,令时间函数φ(t)=1-e-ct,则上式可表示为
上文中Knothe时间函数的函数图像表达了工作面开采后地表点所经历的下沉过程,当t=0时,表示地表点还未下沉,随着时间增加,地表点下沉量逐渐增大,时间t趋于无穷时,则认为地表下沉达到了最大值。有学者指出,其函数的一阶导数反映了工作面开采过程中地表下沉的速度变化趋势,地表下沉加速度变化趋势则与其二阶导数对应。如图1所示,绘制了其函数图像、一阶导数和二阶导数图像。
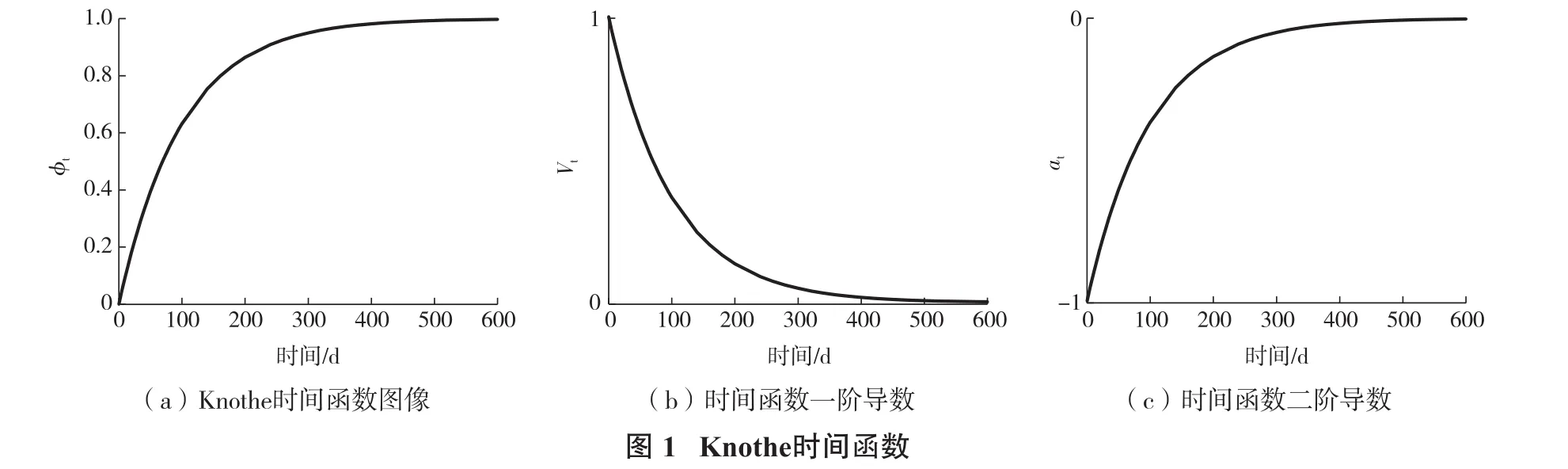
根据工作面地质采矿条件等因素,通过调整时间系数c,以此控制时间函数的取值到达预期的效果。图2给出了地表点下沉量随着不同取值的时间系数c的变化情况。当地表最终下沉量W0设为固定值时,随着时间系数c的增加,地表点下沉到稳定期所需的时间逐渐减少,下沉过程中同一时期的地表点下沉量也随之增大。总而言之,时间系数c的取值反映了工作面开采过程中地表点下沉速度的快慢,取值越大则地表点下沉持续时间越短,下沉过程越剧烈。
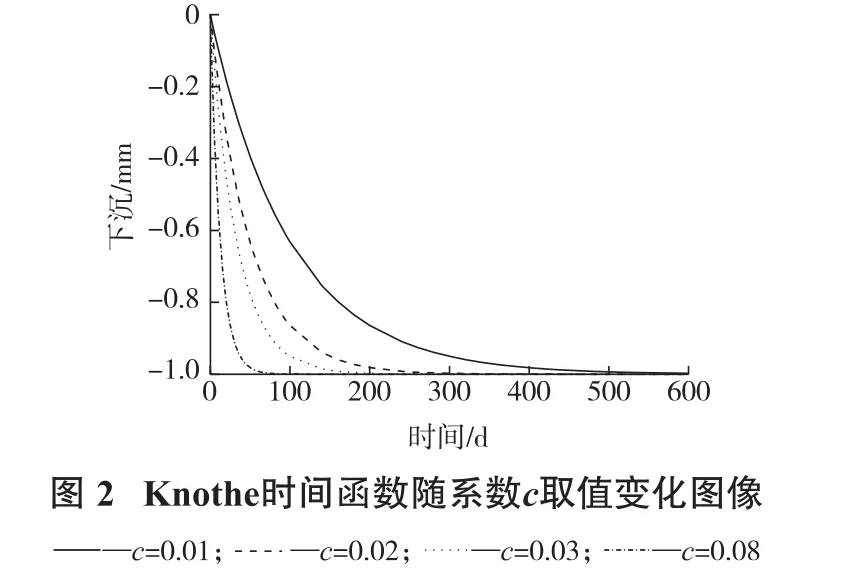
但在实际开采过程中,基于Knothe函数的动态预计效果并不理想。对于这个问题,相关研究表明:在工作面采动初期,地表点的下沉速度较小,此时下沉量缓慢增加,但随着开采的进行,下沉速度逐渐增大,地表下沉量也在短期内快速增加,进入开采后期,地表点下沉速度逐渐下降,地表点的下沉量开始缓慢增长且逐渐停止增长。这一地表下沉过程与分段时间函数的地表下沉是一个静止到加速下沉,再到减速下沉至静止的过程理论相符,因此可考虑采用分段时间函数进行地表沉陷动态预计。
2.2 Knothe时间函数的改进
常占强等[8]通过研究地表点下沉速度的变化规律,提出了采用分段Knothe函数的方法反映地表点的下沉过程,该方法将工作面开采过程中地表点的下沉速度曲线分为两段,且第一段下沉速度曲线与第二段下沉速度曲线关于τ(地表点达到下沉速度最大所需的时间)处对称。则地表点下沉速度V与时间t的函数为
式中,V1(t)和V2(t)为下沉速度函数,分别对应着下沉过程的第一阶段和第二阶段;C为时间函数系数;Ws为最大下沉值;T为下沉总时间。时间函数由式(10)对时间t积分得出下沉时间函数表达式W(t):
改进后的Knothe时间函数引入了地表点下沉速度最大值所需时间,并以此建立了分段时间函数,其函数曲线如图3所示,相较于原来的Knothe时间函数,其函数曲线更加符合地表点的动态下沉过程。
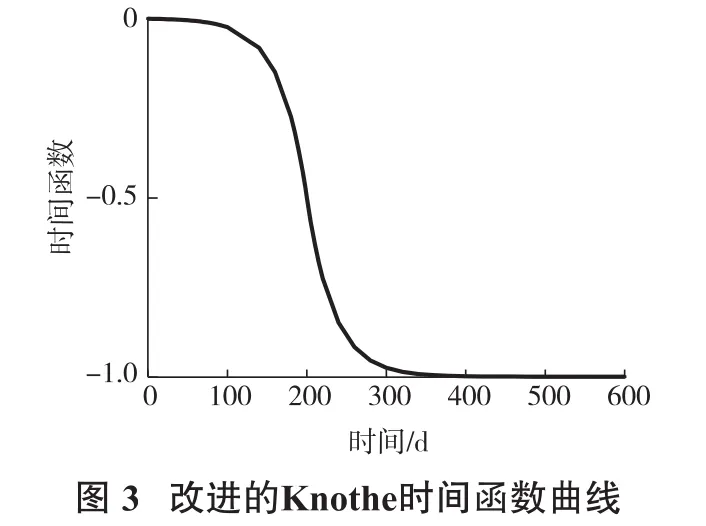
相关研究和实测数据结果表明,近水平煤层开采时,地表下沉最大速度出现的时刻,地表下沉值理论应为地表最大下沉值的一半[9]。如图4所示,当τ值固定,根据不同的参数c绘制改进的Knothe时间函数图形,其最大速度出现的时刻对应的函数值不为最大值的一半。且选取不同的参数c和τ组合,图像函数值未收敛于理论值1。因此分段Knothe时间函数仍存在以下问题:下沉速度最大时刻,时间函数值不为理论值的一半,导致实际预测时会出现预计误差,影响精度;下沉趋于稳定时刻,时间函数的收敛值不为1,导致预计的下沉值将小于理论值。
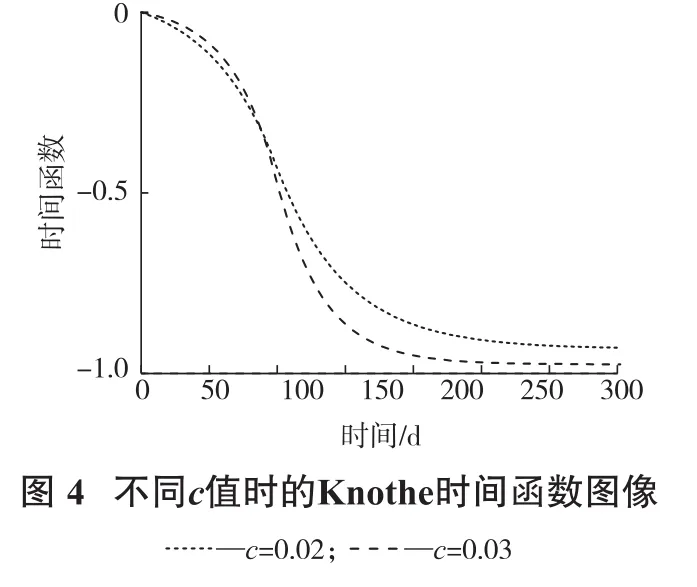
为解决上述问题,将分段Knothe时间函数优化为如下公式:
对上式进行化简,可得:
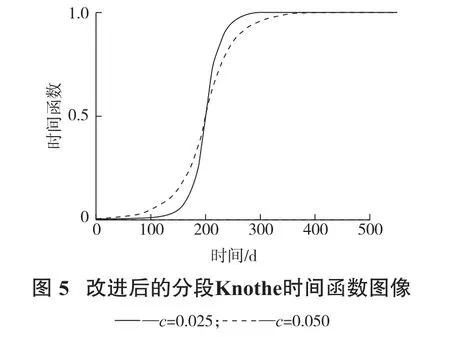
优化后的时间函数图像如图5所示,解决了下沉速度最大时刻函数值不为理论值的一半的问题,且选取不同的参数c和τ组合时,函数也最终能收敛于1,解决了实际运用中的函数导致的误差问题。
3 工程案例
为了评估改进后的山区开采沉陷动态预计模型的精度,采用某矿区3302工作面数据作为验证,基于改进后的Knothe时间函数结合山区开采沉陷滑移模型预计各观测点的下沉,结合实测数据进行分析,并与Knothe时间函数的预计结果进行对比。
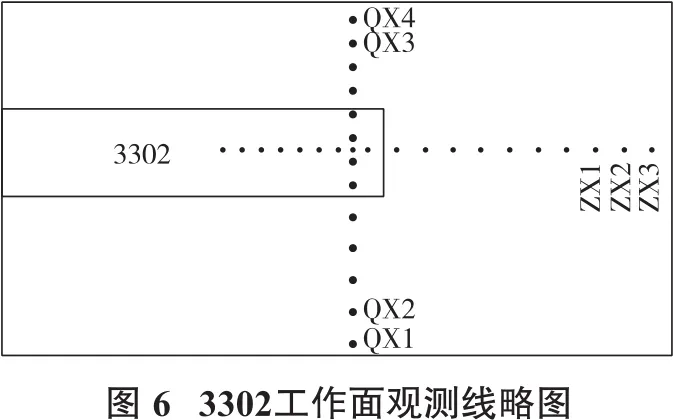
3302工作面地表总地势西北高东南低,属于中低山及山区丘陵地形。走向长2 506 m,倾向长223 m,煤层倾角平均2°,煤层平均厚度5.2 m,工作面走向与X轴方向夹角为6°,煤层平均埋深为280 m。在工作面开切眼一侧布置了半走向观测线和全倾向观测线,共布设了2条观测线,如图6所示。
3.1 基于Knothe函数的动态预计结果精度分析
采用基于Knothe时间函数的模型对观测点下沉进行了预测,并结合实测数据进行对比分析。以工作面边界附近的Q17号点和中部的Q22号点为例,对2点的不同期预计值与实测值进行对比,如图7所示。
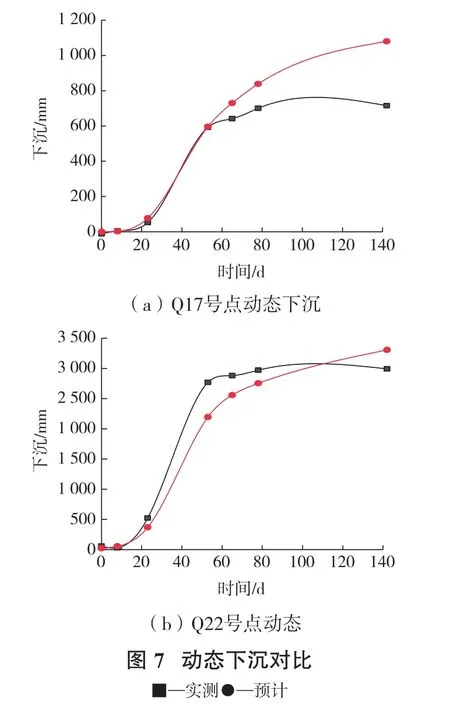
分析图7可以看出,在固定参数基础上,采用Knothe时间函数进行动态预计时,工作面中部和边缘的地表点在采动地表沉陷初期,预测结果接近于实测数据,但随着地表观测点下沉量的增大,预计值与实测值之间的相对误差逐渐增大。这表明Knothe时间函数在实践中存在一定缺陷,其预计结果在地表下沉初期效果较好,但不能很好地反映完整的地表点下沉过程。
3.2 基于改进后的Knothe函数的动态预计结果精度分析
采用基于改进后的Knothe时间函数的模型对观测点下沉进行了预测,并结合实测数据进行对比分析。以2期(第3期和第7期)地表各观测点的下沉实测值和预计值,以及Q17和Q22号点的各期下沉实测值与预计值为例,绘制实测值和预计值的拟合曲线直观对比预计精度,如图8所示。
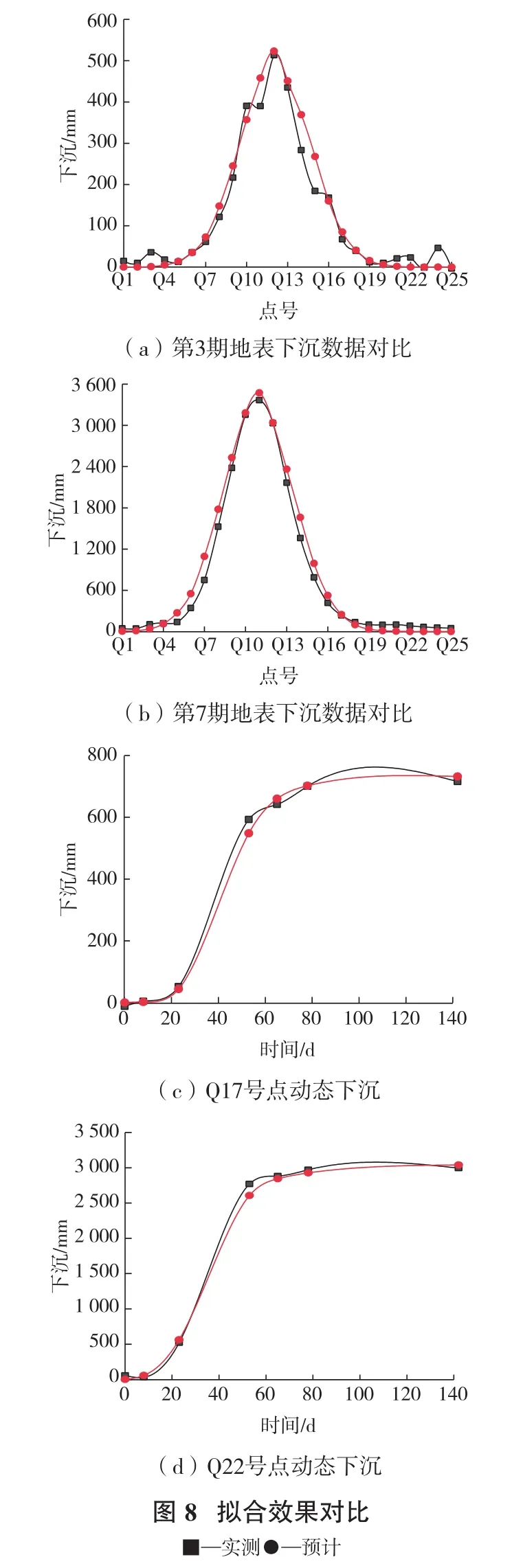
为进一步阐明改进Knothe函数动态预测效果,分别计算了倾向线4期动态预测结果与实测数据之间的中误差,如表1所示。
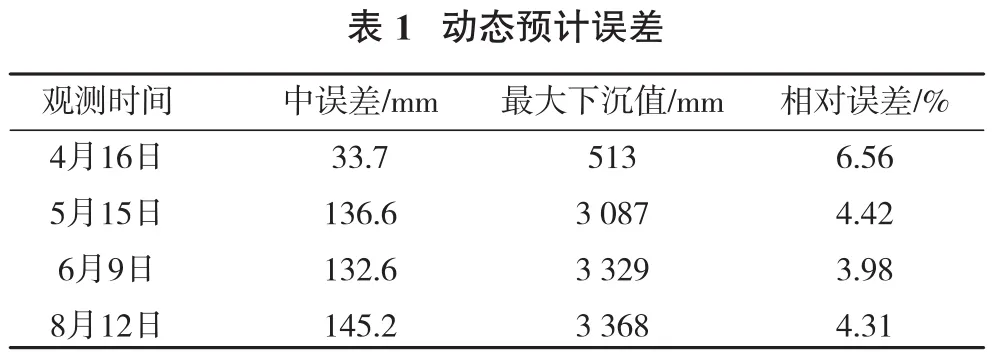
根据计算结果,地表观测点各期预计下沉的中误差最小为33.7 mm,最大为145.2 mm,相对于各期实测最大值的相对误差最小为3.98%,最大为6.56%,结果表明,基于改进后Knothe时间函数的模型预计结果与实测下沉数据具有较好的一致性,动态预计方法取得了良好的工程实践效果。
4 结论
(1)Knothe时间函数具有形式简单,参数易标定的优势。实测数据验证结果表明,Knothe时间函数难以完整描述地表点的沉陷过程,在地表沉陷早期拟合效果较好,后期拟合效果较差。
(2)提出一种改进的分段Knothe时间函数模型进行山区地表沉陷动态预测。实测数据验证结果表明,分段Knothe函数较好地拟合地表沉陷的全过程,地表沉陷最大值预测精度优于7%。

