基于屈曲稳定性的复合材料铺层库优化设计
徐荣章 朱胜利 余明 李咪咪
摘 要:為了得到能便于复合材料结构优化设计同时满足制造约束的复合材料层压板铺层库,本文提出一种基于屈曲稳定性的复合材料层压板铺层库设计方法。首先,独立设计铺层角度数量表,便于多种铺层比例的快速移植和交叉融合;其次,以四进制方式对铺层顺序编码,遍寻满足约束要求的铺层顺序,确定核心铺层组范围,设计稳定性综合评价指标,优化核心铺层组铺层顺序,基于核心层组边界向上和向下逐层扩展,合并得到整个设计空间的复合材料层压板铺层库;最后,分析层压板折算刚度系数推导结果,给出铺层库均匀性调整方法。与手动调试铺层库相比,通过本文方法设计的铺层库临界失稳应力普遍提高10%以上,均匀性调整后的临界失稳应力依然提高5%以上。
关键词:复合材料; 铺层库; 铺层顺序; 屈曲稳定性; 参数优化
中图分类号:TB330.1 文献标识码:A DOI:10.19452/j.issn1007-5453.2023.06.004
基金项目: 国家重点研发计划(2021YFF0500100)
近年来,纤维增强复合材料因其优异的力学特性而被广泛用于航空航天结构设计中,复合材料用量及比重持续增高,已从次承力结构逐渐过渡到主承力如复合材料机翼结构中[1-3]。复合材料机翼结构优化设计通常是指复合材料加筋壁板和翼梁的优化设计,不同于金属机翼,复合材料层压板的各向异性存在较多的设计变量,且变量高度非线性,同时受复合材料铺层连续性约束,使得复合材料机翼参数优化较为困难。
高校和研究机构通常采用多级优化的方式。西北工业大学冯雁和清华大学吴淑一团队[4]按铺层厚度优化、铺层比例优化和铺层顺序优化的三级优化得到最优铺层方案,制造了机翼样件并完成了试验验证。南京航空航天大学王宇等[5]采用等效有限元模型,按“三步走”的结构优化策略依次完成复合材料铺层比例优化、结构效率和结构刚度优化,该策略在初步机翼结构设计时能高效完成优化。朱胜利等[6]对某支线客机复合材料机翼建立有限元模型,分级优化,分阶段实现设计要求,首先完成机翼壁板结构铺层自由尺寸优化,其次完成机翼主翼盒结构多约束参数优化,最后进行工程处理。空客公司尝试采用OptiStruct多级优化策略进行A350复合材料机翼优化设计。多级优化技术虽可使复杂的问题简单化,但也割裂了各级设计变量之间的相互关系,且不便于多轮次的优化迭代,尤其是针对复杂大型复合材料机翼结构参数优化,铺层多达上百层,铺层比例复杂多样,使用多级优化效率较低。
工程设计单位通常采用预设铺层库的方式,设计铺层库能有效解决复合材料铺层连续性问题,显著降低优化变量数和优化复杂度,是一种面向制造工艺的设计方式。史旭东等[7]采用遗传算法对大展弦比复合材料机翼翼梁位置和复合材料铺层进行优化设计,并根据实际工艺要求建立复合材料铺层库。何续斌等[8]在“一种复合材料机翼壁板优化设计方法”专利中设计了铺层库,并基于铺层库完成了机翼壁板的优化。易俊杰等[9]在“一种复合材料铺层库优化生成方法”专利中提出了一种自上而下的铺层库生成方法。
分析上述文献和专利可知,目前主流飞行器设计单位均采用设计铺层库的方式来解决复合材料铺层连续性难题,但当前工程设计单位的铺层库设计主要依靠设计人员的经验和水平手动调试,没有统一的设计标准,也无法完成设计优劣的评价,导致不同设计人员设计的铺层库参差不齐,难以协调,尤其是针对超厚复合材料层压板铺层库的设计,手动调试几乎无法完成。软件公司提出的自上而下的铺层库生成方法不符合工程实际,和工程使用尚有距离。因此,亟须开展复合材料层压板铺层库设计方法和评价方式的研究。
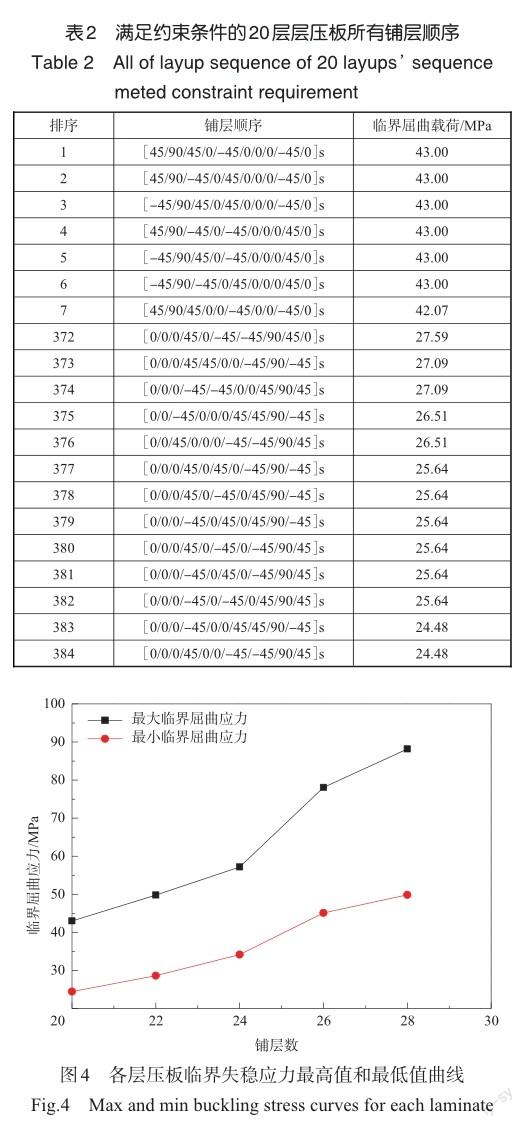
1 铺层库设计流程
基于屈曲稳定性的复合材料层压板铺层库的优化设计流程如图1所示。在复合材料机翼盒段参数优化有限元模型计算中,首先,明确复合材料层压板的设计约束,基于机翼盒段应力分布情况选择合适的铺层比例,针对不同铺层比例设计铺层角度数量表;其次,在设计约束下,动态识别核心层组范围,依据铺层角度数量表,设计稳定性综合评价指标,筛选最优核心层组;最后,依据核心层组铺层,向上逐层加层和向下逐层丢层,直至填满设计空间,组成全设计空间的铺层库,可继续代入参数模型中,优化迭代直至满足设计要求。
本文以某大展弦比机翼盒段参数优化为例,选取复合材料机翼壁板中以承受压缩载荷为主的上蒙皮区域,完成典型蒙皮区域的复合材料铺层库的设计。典型蒙皮格子如图2所示,简化为四边简支矩形平板;材料选用T800碳纤维环氧树脂基复合材料,材料参数为:E1=156GPa,E2= 8.185GPa,υ12=0.33和G12=3GPa,单层厚度0.14mm;设计空间为20~100层。

2 铺层角度数量表设计
承受压缩载荷为主的蒙皮区域复合材料层压板铺层比例一般为0°∶±45°∶90°=5∶4∶1,本文以此铺层比例来设计铺层角度数量表(见表1)。
3 设计约束
对于给定铺层比例的复合材料层压板,在进行铺层顺序设计时应当满足以下约束:(1)相邻铺层角度差不超过60°;(2)同角度最大层组不超过三层,90°铺层不允许叠层;(3)铺层表面至少一层连续。
T800碳纤维环氧树脂基复合材料设计许用值为:(1)压缩许用应变值3800με;(2)拉伸许用应变值4500με;(3)剪切许用应变值5500με。
4 核心铺层库设计 4.1 铺层顺序研究

四边简支复合材料层压板的轴向压缩屈曲载荷计算如下

对于复合材料对称层压板,耦合矩阵为O,铺层顺序的改变不影响面内刚度矩阵,仅影响弯曲矩阵,进而影响层压板的屈曲稳定性。铺层顺序优化的目的是得到满足约束条件下的临界屈曲应力最高的铺层顺序。针对铺层顺序的优化,国内外普遍采用遗传算法寻找最优顺序。修英姝等[12]提出一种分两步的优化体系方法,建立神经网络模型确定规定角度下的铺层数,采用遗传算法优化铺层顺序;罗志军等[13]用组合优化的译码方式和遗传算子对层压板的铺层顺序进行了优化,表明只要搜索解空间的一小部分就能收敛到组合优化问题的最优解。A. K. Dhingra等[14]和 R. L. Riche等[15]均是采用标准遗传算法来求解连续、离散设计变量的结构优化问题,在复合材料铺层顺序优化中均得到良好运用。
本文通过四进制中间状态将铺层字符串(0°/±45°/90°)转换为十进制,实现离散变量到连续变量的转换,图3所示为铺层数为20~26层的满足约束要求的所有铺层。分析可知,每个铺层数一定有两个峰值,对应铺层顺序中45°和-45°互换后的十进制,首次出现峰值的位置相对固定,约在循环总数的27%附近,根据此特征,可快速估算超厚层压板的最优铺层顺序。表2所示为20层铺层时对应的满足约束条件的所有铺层顺序,表中省略了中间的部分铺层顺序,总体而言,45°、-45°和90°铺层越靠外,层压板压缩稳定性越高。
图4所示为铺层数为20~28层的层压板压缩稳定性最高值和最低值曲线图,可知对某厚度铺层,最优铺层顺序比最差铺层顺序的临界失稳应力高约70%,即优化铺层顺序,屈曲稳定性最大能提高70%。每增加一层(对称铺层为二层)铺层,增加厚度后最差铺层顺序的临界值比原最优铺层顺序的临界值低,即不确定铺层顺序优化方向时,增大厚度既增加重量又不一定能提高稳定性。
4.2 确定核心铺层组
按4.1节计算方法遍寻各层压板的最大临界失稳应力,显然,随着铺层数增加,临界失稳应力增加,直到临界失稳应力即将超过一般强度应力约束值,可选取此铺层数为稳定性约束和一般强度约束的分界点,即在此铺层数以下,按稳定性设计,在此铺层数以上,按一般强度设计。设计空间下限至分界点即确定为按稳定性优化控制的核心铺层组。本文以压缩许用应变值3800με为一般强度约束,如图5所示,可知以56层铺层数为分界点,56层以下按稳定性设计,56层以上按压缩许用应变设计,即20~56层为本文算例的核心铺层组。
4.3 生成核心铺层组
层压板的临界失稳应力随铺层厚度增加而增大,临界失稳应力正比于铺层厚度的二次方,可设计归一化指标评价某一层组铺层库铺层顺序的稳定性优劣,铺层库的稳定性综合评价指标如下

由上可知,综合稳定性指数为需要考核稳定性的铺层组中每一个铺层的临界失稳应力比上铺层厚度平方的和,该值越大,表明该铺层组综合稳定性越高。
根据优化参数,以稳定性综合评价指数为优化目标,不断优化核心铺层组顺序,使目标值最大,此铺层组即为核心层组的最优铺层顺序组合。因在参数优化过程中,可不断迭代更新铺层组的边界,故可动态生成核心组铺层顺序。本例中核心铺层组为20~56层,优化后的核心层组铺层顺序见表3。
5 铺层库设计
以核心层组铺层顺序为设计依据,分别向上和向下逐层生成铺层库。以核心层组上边界的铺层顺序为基础,按铺层角度数量表指定的角度,向上增加铺层,增加铺层后需满足设计约束和工艺约束,以获得该层最大临界失穩应力为目标,确定所增加铺层的位置,即确定了该层的铺层顺序,继续按该方法向上生成铺层,一直扩展填满向上的设计空间。以核心层组下边界的铺层顺序为基础,按铺层角度数量表指定的角度,向下丢失铺层,丢失铺层后需满足设计约束和工艺约束,以获得该层最大临界失稳应力为目标,确定所丢失铺层的位置,即确定了该层的铺层顺序,继续按该方法向下生成铺层,一直扩展填满向下的设计空间。核心层组铺层顺序合并向上加层生成的铺层和向下丢层生成的铺层,共同组成整个设计空间的铺层库。

本例中以核心层组上边界即第56层的铺层顺序为依据,逐层向上生成铺层,直至第100层,共同组成整个设计空间的铺层库,见表4。
6 均匀性调整





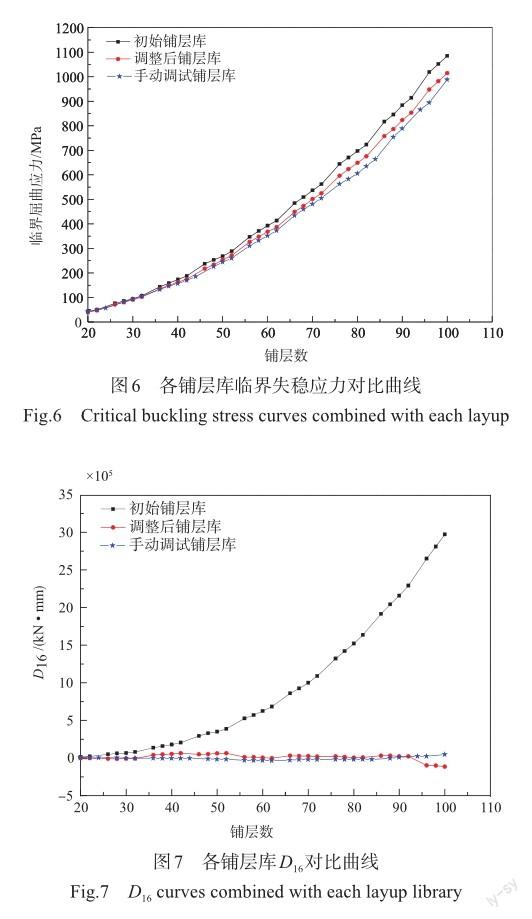
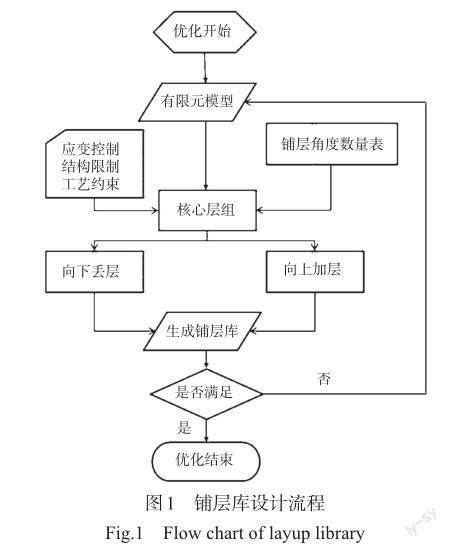
7 结果对比
本文选取工程设计中手动调试的某铺层库作为对比,手动调试的铺层库难免会局部不满足约束。图6所示为各铺层库的临界失稳应力对比图,图7为各铺层库的D16系数对比图,分析可知,按上述方案调整后的铺层库,弯扭耦合系数D16明显降低,与手动调试铺层库的D16数量级相当;调整前铺层库的临界失稳应力比手动调试铺层库普遍提高10%以上,均匀性调整后的铺层库的临界失稳应力依然比手动调试铺层库普遍提高5%以上。

8 结束语
本文提出了一种复合材料层压板铺层库设计流程和方法,明确铺层库的稳定性评价指标,能有效解决手动调试难协调和难评价问题。设计的复合材料铺层库临界失稳应力普遍比传统铺层库提高10%以上。通过均匀性调整后有效降低了铺层库的弯扭耦合系数,且临界失稳应力依然比传统铺层库提高5%以上。
参考文献
[1]杜善义,关志东. 我国大型客机先进复合材料应对策略思考[J].复合材料学报,2008,25(1): 1-10.Du Shanyi, Guan Zhidong. Strategic considerations for development of advanced composite technology for large commercial aircraft in China[J]. Acta Materiae Compositae Sinica, 2008, 25(1): 1-10.(in Chinese)
[2]程健男,徐福泉,张体磊. 树脂基复合材料在直升机的应用及其制造技术[J].航空科学技术, 2021,32(1): 109-114. Cheng Jiannan, Xu Fuquan, Zhang Tilei. Application and manufacturing technology of composite in helicopter[J]. Aeronautical Science & Technology, 2021, 32(1): 109-114.(in Chinese)
[3]Pora J. Advanced materials and technology for A380 structure[J]. Fast Magazine, 2003, 32: 3-8.
[4]冯雁,郑锡涛,吴淑一,等. 轻型复合材料机翼铺层优化设计与分析[J]. 航空学报,2015,36(6): 1858-1866. Feng Yan, Zheng Xitao, Wu Shuyi, et al. Layup optimization design and analysis of super lightweight composite[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1858-1866.(in Chinese)
[5]王宇,欧阳星,余雄庆. 采用等效有限元模型的复合材料机翼结构优化[J].复合材料学报, 2015,32(5): 1487-1495. Wang Yu, Ouyang Xing, Yu Xiongqing. Structural optimization of composite wing using equivalent finite element model [J]. Acta Materiae Compositae Sinica, 2015, 32(5): 1487-1495. (in Chinese)
[6]朱胜利,姚雄华,刘红武. 复合材料机翼翼盒结构多约束参数优化设计[C].第16届全国复合材料学术会议,2010: 96-104. Zhu Shengli, Yao Xionghua, Liu Hongwu. Multidisciplinary sizing optimization design of a composite aircraft wing-box[C]. The 16th National Composite Materials Conference, 2010: 96-104. (in Chinese)
[7]史旭東,陈亮,张碧辉,等.基于遗传算法的大展弦比复合材料机翼结构优化设计[J].航空工程进展,2015,6(1): 110-115. Shi Xudong, Chen Liang, Zhang Bihui, et al. Structural optimization design of high aspect ratio composite wing based on genetic algorithm [J].Advances in Aeronautical Science and Engineering, 2015, 6(1): 110-115. (in Chinese)
[8]何续斌,黄文超,孟维宇,等. 一种复合材料机翼壁板优化设计方法:中国,ZL 201610771638.4 [P]. 2019-05-10. He Xubin, Huang Wenchao, Meng Weiyu, et al. A composite material wing wall optimization design method: Chinese, ZL 201610771638.4 [P]. 2019-05-10.(in Chinese)
[9]易俊杰,吴宏升. 一种复合材料铺层库优化生成方法:中国,ZL201810700601.1 [P]. 2020-01-24. Yi Junjie, Wu Hongsheng. Composite material layup library optimization generation method: Chinese, ZL201810700601.1[P]. 2020-01-24.(in Chinese)
[10]顾诵芬. 飞机复合材料结构设计与分析[M]. 上海:上海交通大学出版社,2011. Gu Songfen. Design and analysis of composite structures[M]. Shanghai: Shanghai Jiao Tong University Press, 2011. (in Chinese)
[11]趙占文,苏雁飞,崔勇江. 变刚度复合材料层压板的轴压稳定性优化研究[J].航空科学技术, 2021,32(8): 57-61.Zhao Zhanwen, Su Yanfei, Cui Yongjiang. Buckling optimiza‐tion study on variable stiffness composite laminate under com‐pression load[J]. Aeronautical Science & Technology, 2021, 32(8): 57-61.(in Chinese)
[12]修英姝,崔德刚. 复合材料层合板稳定性的铺层优化设计[J].工程力学, 2005,22(6): 212-216. Xiu Yingshu, Cui Degang. Ply optimization design for stability of composite laminates [J].Engineering Mechanics, 2005, 22(6): 212-216. (in Chinese)
[13]罗志军,乔新. 基于遗传算法的复合材料层压板固有频率的铺层顺序优化[J].复合材料学报,1997,14(4): 114-118. Luo Zhijun, Qiao Xin. Optimization of ply stacking sequence for natural frequencies of composite laminates by genetic algorithm [J]. Acta Materiae Compositae Sinica, 1997, 14(4): 114-118. (in Chinese)
[14]Dhingra A K, Lee B H. A genetic algorithm approach to single and multi objective structural optimization with discrete continuous variables [J]. Numerical Methods in Engineering, 1994, 37: 4059-4080.
[15]Riche R L, Haftka R T. Optimization of laminate stacking sequence for buckling load maximization by genetic algorithm[J]. AIAA Journal, 1993, 31: 951-956.
Optimization Design of the Composite Layup Library Base on Buckling
Xu Rongzhang, Zhu Shengli, Yu Ming, Li Mimi
AVIC The First Aircraft Institute, Xi’an 710089,China
Abstract: In order to obtain the composite layup library that can facilitate the optimal design of composite structures while meeting manufacturing constraints, a method dealing with composite laminate layup library base on buckling was proposed. Firstly, a table of layup angle was designed, which will be convenient for fast migration and cross fusion with each ration of layup angle. Secondly, the layup sequence was encoded by quaternary. All of layup sequence meted constraint requirement were computed. The range of core laminate was determined by a comprehensive index of buckling was defined. The layup sequence of core laminate was optimized, ply was developed upwardly and downwardly, then a composite laminate layup library in the whole design space was combined with each other. Finally, the improved evenly method of layup library was determined. The critical buckling stress of this composite laminate layup library will increase by more than 10% compared with manual layup library. The bending-torsion coupling coefficient is reduced effectively by improving evenly, and the critical buckling stress will still increase more than 5%.
Key Words: composite; layup library; layup sequence; buckling; parameter optimization