基于ANFIS的氧化稀土浓度控制研究

徐墨暄，王新春

内蒙古科技大学信息工程学院，内蒙古包头，014010

0 引言

稀土元素是一类具有重要战略地位的特殊金属，广泛应用于国防、高科技和新能源等领域。然而，稀土资源的开发与利用一直受到限制，主要原因是其分布较为零散，存在量也较为有限[1]。稀土熔盐电解技术作为一种先进的稀土元素提取工艺，具有高效、环保等优势，并且可以获得纯度较高的稀土金属。此外，该技术可以将稀土氧化物转化为稀土金属，从而减少环境污染和资源浪费，符合可持续发展的理念。因此，稀土熔盐电解技术的应用对于保障稀土资源的供应和促进我国稀土产业的发展具有十分重要的意义[2]。现场调研显示，大多数稀土电解厂依赖车间工人手动添加氧化稀土，少数使用定时下料装置。由于缺乏直接监测氧化稀土浓度的传感器，物料添加量取决于生产工人经验，目前采取过量添加的方式，几乎没有考虑到电解槽内氧化稀土浓度的状况。而现阶段氧化稀土浓度的测定还停留在实验室中进行，对氧化稀土浓度的控制更是尚未研究与提及。

1 氧化稀土浓度影响因素分析

稀土电解是一个连续的生产过程，氧化稀土持续消耗。车间工人持续不断地添加氧化稀土，新加入的氧化稀土随着电解反应逐渐溶解，导致稀土电解槽内的氧化稀土浓度一直处于波动变化状态。用公式（1）来定性描述电解槽内氧化稀土的质量：

式中：Mt1表示在t1时刻电解槽内氧化稀土的质量，单位为kg；Vdep表示氧化稀土的消耗速率，单位为kg/s；t为从t0到t1所需的时间，单位为s；Mdis表示t0至t1期间氧化稀土的溶解量。下料量是氧化稀土浓度变化的直接影响因素。

以物质平衡关系计算氧化稀土的消耗速率：理论上只需要计算出电解槽中氧化稀土的消耗速率，再以消耗速率加料，就可以达到物料平衡[3]。电解槽的理论产量只与其电流强度有关，如果电流用I（kA）来表达，那么该电解池的理论产量为1.7942×I，设电流效率为η（%），则每小时的实际稀土产量为：1.7942×I×η。按照化学反应式可以从氧化稀土的分子式计算出每产出1千克钕理论消耗量，计算过程如式（2）：

通过计算得x=1.167kg，即每产出1千克金属钕理论上需要消耗1.167kg的氧化钕。由此可知，电流强度为I千安（kA）、电流效率为η的电解槽，每小时（h）的氧化钕理论消耗量（Fc）为1.167×1.7942×η×I（kg），如式（3）：

对应的每分钟氧化稀土（氧化钕）的理论消耗量（Fc）如式（4）：

本文稀土电解槽选型为8000A，电流效率为80%，用上式计算可得氧化稀土的理论消耗速率约为0.223kg/min。氧化钕在氟化物电解质熔盐中的溶解度约为4%[4]。影响氧化稀土溶解因素很多。在稀土电解生产的正常过程中，加入电解槽中的氧化稀土需一定时间溶解才能被电离。因此，氧化稀土电解过程具有较大的滞后性，目前对于氧化稀土在氟化物体系中的溶解曲线研究较少，尚未有明确的结论。电解稀土熔盐过程中，氧化稀土的下料直接影响槽内浓度变化，为了确保电解槽平稳运行，就必须使加入的物料与其电解的消耗达到一个平衡的状态[5-6]。若加料量少于消耗所需的氧化稀土量，则氧化稀土浓度将会减少，而减少至某一阈值时，就会产生阳极效应，导致电解槽无法继续运行；若加料量超过电解所需的量，则会使浓度升高，达到一个临界点时，氧化稀土从电解液中析出，并形成沉淀，造成浪费和其他许多问题[7]。因此，合理控制氧化稀土的添加量对于稀土电解过程的平稳运行和产品质量具有至关重要的作用。

2 稀土氧化物浓度状态监测方法

在铝电解领域中，氧化铝浓度对槽电阻有着很大的影响，实验表明二者呈现出一种“U型”关系，即在特定的氧化铝浓度下槽电阻达到最低值[8]。现阶段对于稀土下料控制的研究匮乏，但稀土电解与铝电解的生产过程极为类似，许多铝电解的理论可以借鉴在稀土电解工艺上。稀土电解下料的过程控制是将电解槽中氧化稀土的浓度控制在一个合理范围。

由图1可以看出，极距变化只会引起曲线的高低产生变化。现阶段稀土电解过程中，可以在线检测的参数有槽电压、槽电流以及熔盐温度[9]，与现代铝电解计算槽电阻方法相似，槽电阻R是槽电压U与槽电流I计算得到的参数，经过低通滤波尽可能减小采样设备以及电解槽运行过程中产生的噪声后，被用来作为稀土电解过程控制的主要参数。其计算公式如式（5）：

图1 槽电阻-浓度曲线

式中，R表示原始槽电阻；U表示槽电压；I表示槽电流；B表示表观电动势，通常为一常数。

电阻R对浓度C的变化率与槽电阻斜率之间存在下式关系：

dR/dC表示电阻R对浓度C的变化率，dR/dt表示槽电阻斜率，dC/dt表示浓度对时间的变化率。

当槽况正常时，在电解过程中以某种既定的频次下料，使得dC/dt≠0且基本稳定时，斜率dR/dt与dR/dC成正比，在这种既定的下料频率前提下，通过电阻斜率就可以大概推断出对应时刻的氧化稀土浓度的范围，如图2所示。

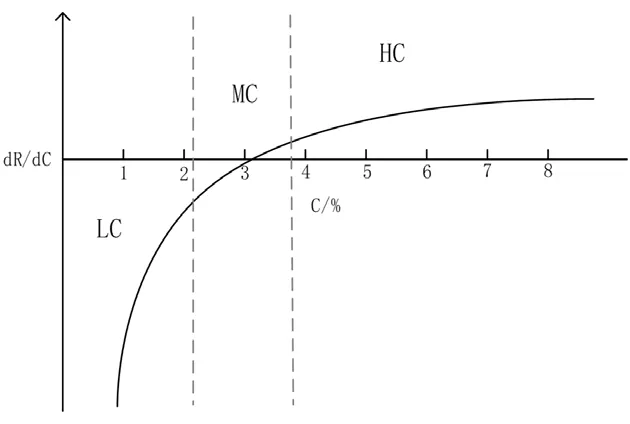
图2 氧化稀土浓度-浓度变化率曲线

3 浓度自适应神经模糊控制系统设计

在实际应用中，通常采用手动方式，依靠专家经验进行调整，这样调节效率、精度较低。神经网络具有自适应学习能力，可以通过应用自学习技术来进行模型特征分析和建模。而在此基础上，将其与模糊控制相融合，使其具有更强的表达能力与学习能力。由于稀土电解是一个非线性、时变、大滞后系统，无法计算出氧化稀土浓度与下料速率之间的准确模型，在实际设计时，需要不断调整控制器参数，以达到更好的效果。ANFIS建模具有自适应能力，鲁棒性强，能用于绝大多数的非线性模型的建模的特点。因此本文提出一种通过ANFIS整定模糊控制器的方法[10]。

ANFIS训练完成的模型为T-S模糊控制器，输出量是输入量的线性函数。与传统的Mamdani模糊控制器相比，T-S模糊控制器没有清晰化的模块，并且其推理结果直接产生清晰值，使用清晰的输出函数代替了模糊蕴含关系。并且ANFIS训练完成的模型不具备可解释性。ANFIS结构如图3所示。

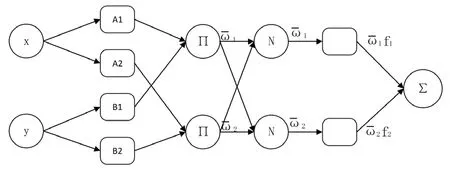
图3 ANFIS 结构示意图

ANFIS模型结构一般分为五层。

第一层：将输入变量模糊化，输出对应模糊集的隶属度函数，该层每个节点i都具有节点函数[11]。

其中，x是节点i的输入；Ai是与该节点相关的不同标签；Oi1是Ai的隶属度函数；指定给定x满足Ai的程度，通常选择高斯隶属函数：

第二层：该层的每个节点都是一个标识为∏的圆形节点，将输入信号相乘并输出。

第三层：归一化层，第i个节点计算第i条规则的触发强度占所有规则触发强度之比。

第四层：该层的每个节点都是一个节点函数，每个传递函数为线性函数。

第五层：计算所有规则的输出之和作为整体输出。

通过ANFIS对稀土电解过程数据进行训练，设置训练数据为两输入一输出，输入数据同模糊控制器输入为槽电阻（浓度）变化量与其变化率，输出数据为下料速率。

图4为ANFIS学习算法流程图。传统BP算法搜索空间尺度大，容易造成局部极小，收敛速度慢，选用混合算法有效地改善了其缺点。混合学习算法是指将最小均方误差（MSE）和最大似然估计（MLE）两种学习算法结合起来使用。

图4 ANFIS 学习算法流程图

（1）计算前向传播的输出值

其中，wn是第n个规则的权重，An是第n个规则的输出。

（2）损失函数E

其中，Y是样本的输出值，O是ANFIS模型计算出来的输出值。E表示预测输出值和真实输出值之间的平均误差。

（3）损失函数L

其中，P（Y|X）是模型对于给定输入X时输出为Y的概率。L表示最大化整个数据集的似然估计值。

（4）计算整体损失函数

其中，w是一个权重参数，用于平衡E和L两种损失函数的影响。

反向传播误差并更新各层的参数，更新模糊规则库中每个规则的后件部分（即用于计算输出值的隶属函数）的参数以及前件部分（即用于计算输出值的输入变量）。

根据损失函数以及计算出的误差信号，使用梯度下降算法更新规则后件部分的参数。由于ANFIS训练所得为T-S模糊控制器，控制器输出为具体下料速率值。图5为学习后输入输出映射关系三维曲面。

4 控制系统仿真

通过ANFIS算法自整定模糊控制器，通过MATLAB进行仿真，PID控制器比例、微分、积分控制器系数取值分别为：0.17、0.05、0.21。

给定输入阶跃信号，并在50s处施加噪声阶跃，对比传统PID控制与ANFIS的控制效果如图6，可以看出，相比PID控制器，ANFIS超调量更小[12]。

图6 PID 和ANFIS 控制效果对比

利用包头某8000A规模稀土厂实际采集数据，以2秒为采样周期，对槽电压U和槽电流I进行同步采样，计算出槽电阻R。稀土熔盐电解过程中由于从下料、溶解、反应到槽电阻变化需要一定的时间，系统惯性较大，并且其受多因素影响，抵抗外界干扰能力不强。二阶传递函数可以很好地描述系统的惯性和阻尼特性。本文选用二阶滞后模型，通过将浓度与下料速率数据导入MATLAB进行参数辨识，结果如式（17）：

由图7可以看出，经过ANFIS模型训练得到模糊控制器，将其导入simulink中进行仿真。图中红色线信号代表控制后的槽电阻曲线，可以看出，槽电阻的变化范围更加平缓，其控制效果明显优于一般的模糊控制器，对比如图8所示。

需要说明的是，现阶段稀土熔盐电解的研究与氧化稀土浓度相关的内容鲜有报道，电解槽内氧化稀土最佳浓度值尚未有统一的标准。本文槽电阻的数据选取的是稀土厂工人根据经验手动下料控制数据，本文对槽电阻与氧化稀土浓度关系进行了定性分析，忽略了槽况异常、电解质组成参数的变化、阳极消耗过多、换阳极等情况。

5 结论

稀土电解工艺复杂，难以得出精确的数学模型，使用ANFIS模型生成模糊控制器，得到控制效果，将传统PID与ANFIS模糊控制器控制效果做对比，得到仿真结果表明：ANFIS模糊控制器仿真曲线更为平滑，在控制效果上更加稳定，在系统动态特性等方面优于传统PID控制器。