智能控制理论与智能电器教学的融合
汤龙飞, 陈 炜, 许志红
(福州大学a.电气工程与自动化学院;b.智能配电网装备福建省高校工程研究中心,福州 350108)
0 引言
电器控制技术是伴随着自动控制理论的发展而逐步发展的。从经典控制理论到现代控制理论,再到智能控制理论,各种自动控制理论被逐步应用到开关电器控制领域,提高了电器的智能化水平及分合闸能力,进而提高电力系统的控制灵活性及安全稳定性[1]。
经典控制理论以拉普拉斯变换为数学工具,以单输入单输出的线性定常系统为主要研究对象,将描述系统的微分方程或差分方程变换到复数域中,得到系统传递函数,并以此为基础在频域中对系统进行分析与设计,确定控制器的结构和参数[2]。文献[3]中采用经典控制理论及Buck 拓扑设计了接触器的电流闭环PID控制方案,该方案将接触器电磁回路看作恒定阻感负载,构建闭环控制系统的小信号模型,采用交流扫描得到系统伯德图,分析系统的相位裕度及幅值裕度,进而设计补偿网络,兼顾电流闭环控制系统的动态性能及稳定性;文献[4]中采用可级联的升压电路及馈能去磁电路,在电流闭环基础上实现了接触器超宽电压输入下的低噪声运行及分断速度调节,之后同样将接触器视作恒定阻感负载,采用小信号分析方法来设计控制系统的补偿网络。因此,经典控制理论应用于接触器的控制领域中实现了其线圈电流的闭环控制,但在设计补偿网络时需将接触器电磁回路视作恒定阻感,即假设为线性定常系统,与接触器动作过程的实际工况有较大出入[5]。
现代控制理论以线性代数和微分方程为数学工具,以状态空间法为基础,从时域角度来分析与设计控制系统。状态空间法不仅描述了系统的外部特性,还揭示了系统的内部状态。现代控制理论的目标是在揭示系统内在规律的基础上,实现系统的最优化,其主要分支有:线性系统理论、最优滤波理论、系统辨识、最优控制、自适应控制及非线性系统理论[6]。文献[7-8]中采用状态空间法列写接触器保持过程的状态空间表达式,构建保持磁链的闭环状态观测器,结合起动及分断过程的积分磁链观测器,实现了接触器磁链的全程观测,之后用作负反馈形成磁链闭环控制系统,实现了接触器激磁磁链的直接控制。文献[9]中采用加权移动平均滤波器对接触器的线圈电流和电压进行滤波,来准确捕捉动静铁心的闭合时刻及此时的电流值,据此降低保持电流,实现自适应节能控制。文献[10]中对接触器线圈电压的幅值与作用时间进行模型预测控制,以响应时间最短为优化准则,同时确保动静触头相接触时速度为零,实现触头弹跳抑制。文献[11]中基于批次对批次(Run-by-Run,RBR)控制方式对接触器的吸合过程展开研究,引入损失函数对历史操作信息进行反馈评估与分析,滚动优化过程模型并调整控制决策,有效减小了接触器的动作分散性并抑制触头弹跳。文献[12]中设计兼顾快速动作和弹跳抑制的接触器吸合过程电流闭环控制序列,寻找线圈电流与动作时间的直接关系,之后引入无模型自适应控制对电磁机构吸合过程进行在线优化,以抑制动作分散性及触头弹跳。以上基于现代控制理论的接触器控制方案均不同程度地优化了起动性能,但仍无法对接触器的电磁力、位移及速度构成直接的闭环控制。
智能控制是控制理论发展的高级阶段,将人工智能技术及运筹学优化方法与控制理论结合,在未知环境下仿效人或生物的智能,实现对系统的控制,主要涵盖模糊控制、专家系统、神经网络、遗传算法等学科领域[13]。智能控制理论应用于电器实时控制的研究尚少,大部分人工智能方法仅用于电器的故障诊断及状态预测[14-15]。文献[16]中根据位移传感器测得的信号,采用带自调整函数的模糊算法来控制永磁机构的激磁电流,使断路器按给定曲线动作,提高合闸稳定性。文献[17]中采用神经网络估计接触器动铁心的运动速度,之后采用模糊控制逐次调整线圈强激磁电流的作用时间,使合闸速度逐次趋近于给定值。以上两种控制方法初步实现了开关电器位移及速度的闭环调整。
接触器动作过程是一个复杂的非线性、强耦合且快速时变的系统,无法采用经典及现代控制理论建立其“精确的实时解析模型”,制约着接触器的高性能控制,而智能控制理论恰恰擅长解决此类问题。因此,本文引入神经网络对接触器电磁机构“二元一一对应”的静态机电关系进行映射,构建电磁吸力观测器;采用三位式滞环控制器构建接触器直接吸力闭环控制策略,实现接触器电磁吸力的精确控制。整个控制方案采用灵活、直观地联合仿真及快速控制原型验证系统予以实现,展示控制原理的实现过程,并方便控制方案的改写,用于进一步自主探索智能控制理论在智能电器中的应用。
1 接触器静态机电关系映射
1.1 神经网络映射原理
利用有限元软件构建接触器仿真模型,在每个不同的固定动铁心位移下加载一系列的线圈电流值,得到接触器静态磁链及吸力数据,并将其绘制到图1 所示三维图中。以线圈电流icoil,磁链ψ约束对为底面,穿竖直直线,有唯一的电磁吸力Fx与之对应,即存在着(icoil,ψ)→Fx“二元一一对应”的非线性静态映射关系。而神经网络具有强大的非线性拟合能力,可对该映射关系进行拟合,实现已知接触器的线圈电流及磁路磁链估计电磁吸力,进而构建基于神经网络的吸力实时观测器。
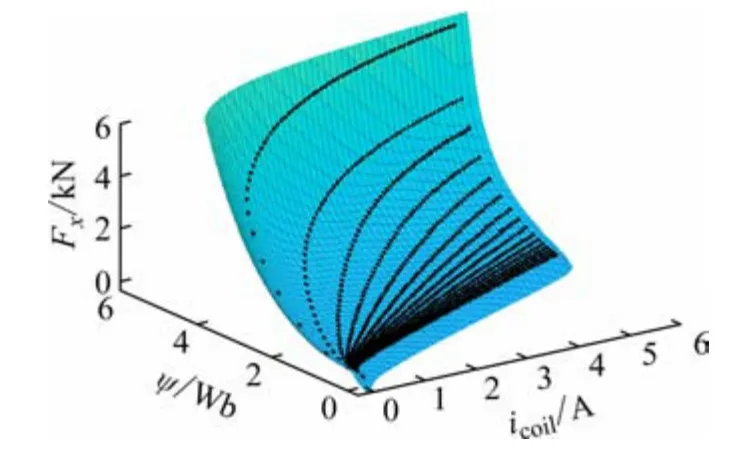
图1 静态机电数据对应关系
采用图2 所示的单隐含层BP 神经网络即可满足接触器静态映射关系拟合精度的要求,同时便于实时应用。两个输入节点icoil及ψ经隐含层神经元权值Wij与阈值aj叠加后输入激活函数tansig计算,输出yj;之后yj作为输出层网络的输入,经输出层权值Wj与阈值b的叠加及激活函数的计算即可输出观测吸力Fx,具体计算过程为:
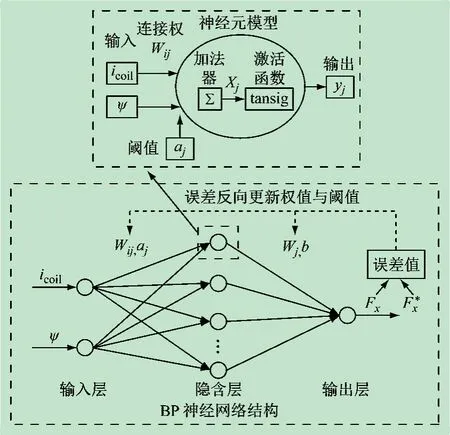
图2 BP神经网络模型结构
式中:xi为输入层的输入信号,即线圈电流及磁链;M为设定的隐含层节点个数。
计算观测值Fx与期望输出F*x的误差,并进行反向传播:根据误差的大小和方向,采用“梯度下降法”修正神经网络的权值及阈值,直至达到预先设定的最大训练次数或输出误差满足要求。训练完成后即可根据输入的(icoil,ψ)映射出电磁吸力Fx。
1.2 电磁吸力实时观测器构建
利用上述BP神经网络的高精度映射能力构建电磁吸力实时观测器,由图3 可见,将电磁系统(icoil,ψ)→Fx的一系列静态数据作为二元输入,电磁吸力Fx作为期望输出,对BP神经网络进行离线训练,训练完成后进行嵌入式改写即可用于静态机电关系的实时映射。根据公式:
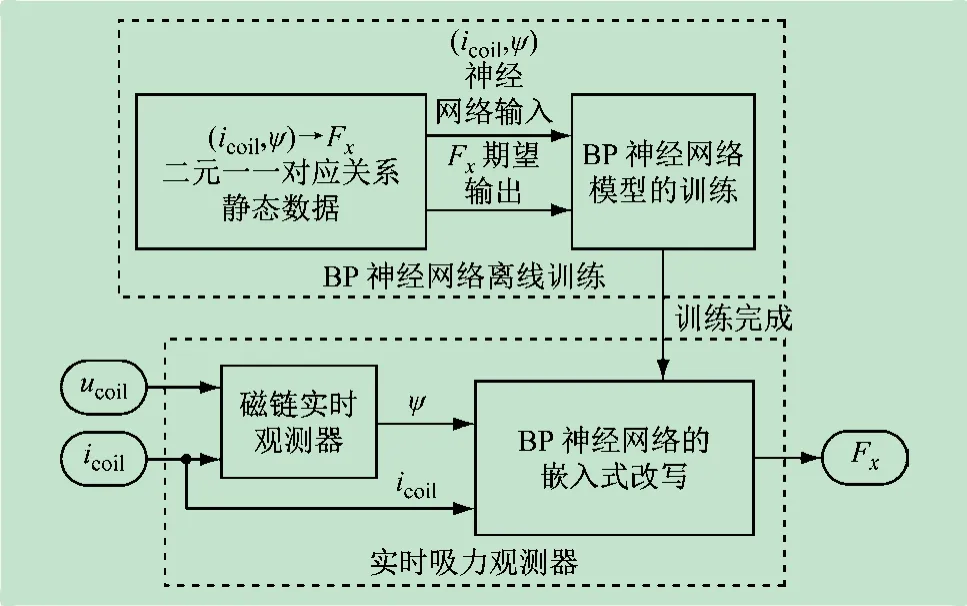
图3 电磁吸力实时观测器原理
式中:Rcoil为离线测量的接触器线圈电阻;t为观测器工作的时间,初始磁链ψ、线圈电压ucoil及线圈电流icoil皆为0。构建磁链观测器,仅需利用传感器采集接触器的线圈电压ucoil和线圈电流icoil即可实时计算磁链ψ。最后,将icoil、ψ输入到嵌入式神经网络模型,即可实时映射出Fx,完成吸力实时观测器的构建。
吸力观测器中BP 神经网络的离线训练可利用Matlab软件的nntool 神经网络工具箱方便地完成,如图4 所示,将静态数据(icoil,ψ)→Fx作为样本,取其中的2/3 用于训练,剩下1/3 用于检验。设置BP神经网络为单隐含层结构,其中隐含层的神经元个数为15;激活函数采用双曲正切函数(tansig);训练函数采用Levenberg-Marquardt算法(误差梯度下降法);学习率设为0.1;训练的最小性能精度min_grad设为10-7;最大连续验证误差不减小次数max_fail设为10 次;训练的最大终止次数设为1000 次。
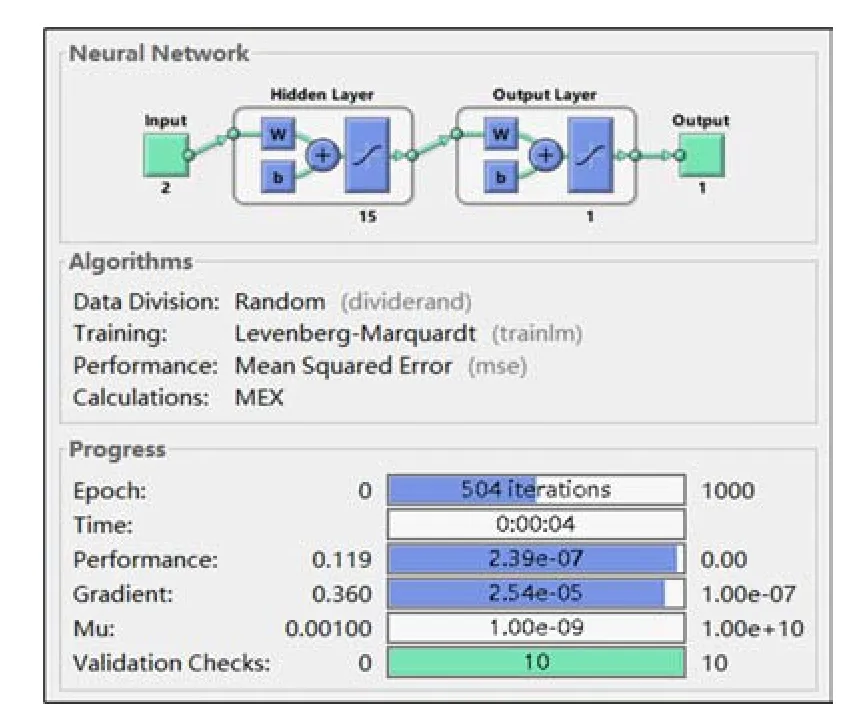
图4 BP神经网络训练过程
神经网络拟合精度采用均方误差mse 来表示,在误差梯度曲线连续第10 次迭代不再下降时,训练终止。整个过程的训练次数为504 次,时间仅用4 s,mse最小值达到2.39 ×10-7,满足拟合精度要求,离线训练完成。提取神经网络模型的前向网络,包括各网络层的权值与阈值,按照式(1)的计算结构改写成嵌入式形式,即可实现对难以直接测量的接触器电磁吸力Fx的实时观测。之后将其用作反馈信号,构建接触器的高性能闭环控制策略。
2 接触器直接吸力闭环控制原理
2.1 线圈驱动原理
驱动电路采用非对称半桥结构,如图5 所示,分为励磁、续流以及去磁3 种状态。交流电压(220 V)经整流桥及滤波电容C1作用后输出直流电压Uc,用作驱动电路的输入电源。S1、S4为电子开关管,D2、D3为快恢复二极管。当上下桥臂开关管S1、S4同时导通时,加在线圈两端的电压近似为正的电容电压,即励磁状态;当S1关断、仅下桥臂开关管S4导通时,线圈电流经过D3、S4形成闭合回路,此时线圈两端电压为二极管与开关管的导通压降和,近似0 V,即续流状态;当S1、S4同时关断时,线圈电流经D2、D3回馈至电容,线圈两端承受负的电容电压,为去磁状态。该3 态驱动电路可灵活地控制开关管S1及S4的通断,进而灵活控制电磁系统的激磁状态,为接触器闭环控制提供硬件基础。
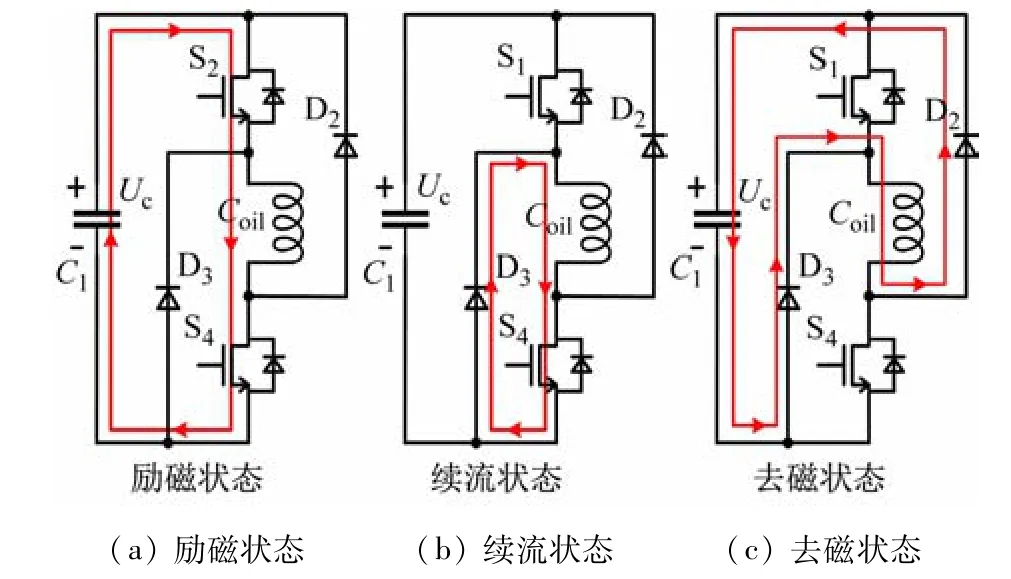
图5 非对称半桥驱动电路3种工作状态
2.2 电磁吸力三位式滞环控制原理
在驱动电路的3 种状态划分后,即可针对不同的吸力误差范围选择合适的开关状态组合,来构建三位式吸力滞环控制器,原理如图6 所示。控制器的运行频率为fs,Fr为吸力参考值。将Fr与观测吸力Fx作差,得到吸力误差Fe,再与设定的滞环宽度ε 比较。当Fe<0 时,选择励磁电路状态,使电磁吸力快速上升;0≤Fe≤ε时,选择续流电路状态,电磁吸力缓慢下降;Fe>ε时,选择去磁电路状态,电磁吸力快速下降。之后,将对应的电路状态转换成S1及S4的开关状态,即可控制电磁吸力的变化方向及变化速度,进而实现电磁吸力快速跟踪参考吸力。
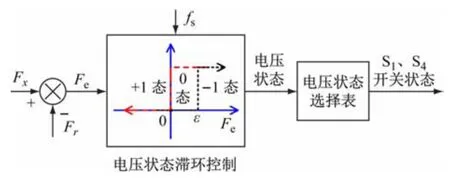
图6 三位式吸力滞环控制器
结合上述吸力观测器、线圈驱动电路及三位式滞环控制器构建图7 所示完整的接触器直接吸力闭环控制方案,利用吸力误差直接选择驱动电路的电压状态,将电磁吸力快速控制在滞环误差范围内,实现了接触器电磁吸力的直接闭环控制。
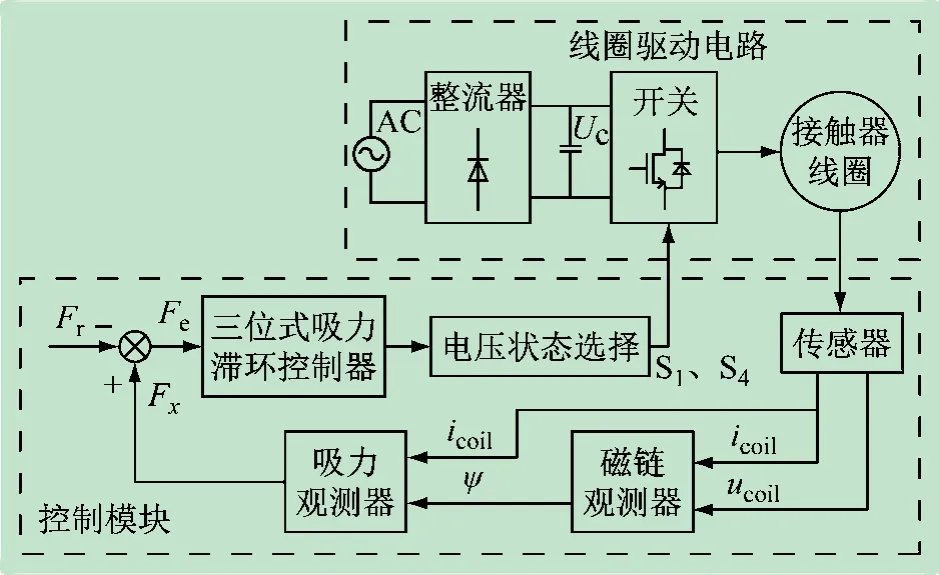
图7 直接吸力滞环控制原理
3 仿真分析
采用LabVIEW 和Multisim 构建智能接触器的联合仿真系统,集硬件控制电路、软件控制策略和接触器本体于一体,仿真接触器的直接吸力闭环控制方案,联合仿真的具体构建方法见文献[18]。仿真中滞环频率fs设为20 kHz,滞环宽度ε设为10 N。接触器完全吸合时弹簧反力Ff最大为340 N,留有一定裕量,将起动和保持吸力参考值Fr均设为400 N,保证接触器可靠工作。波形如图8 所示,包括起动、保持和分断过程。
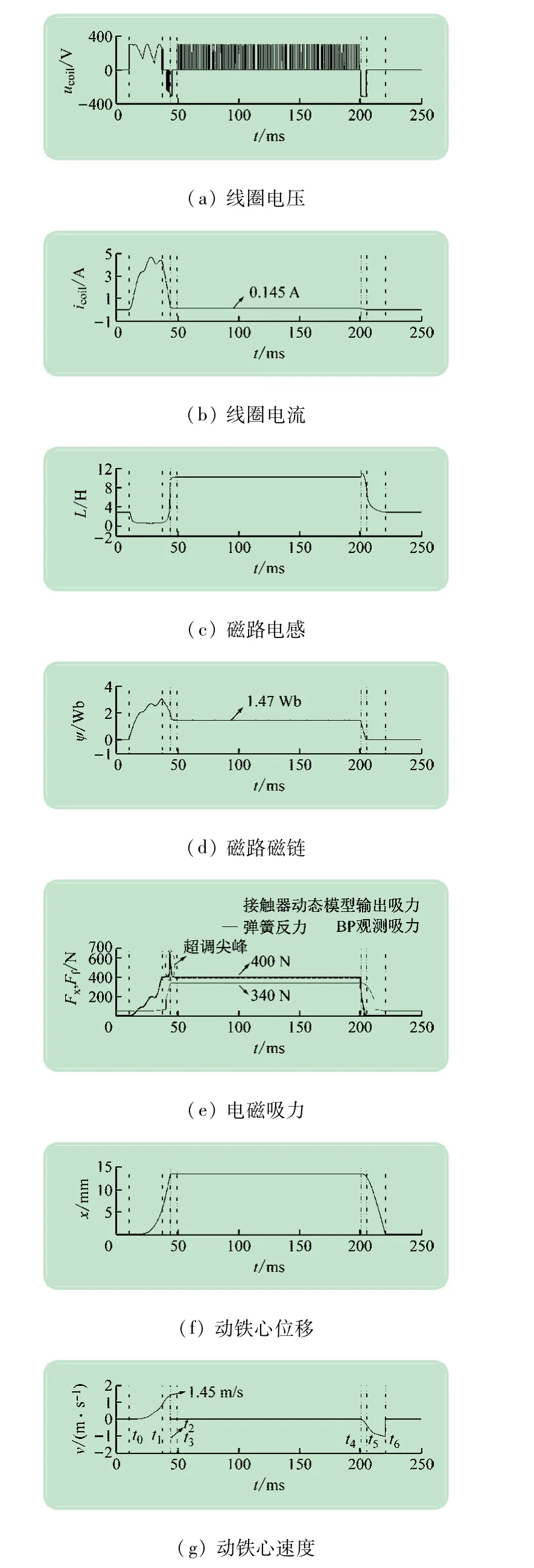
图8 吸力闭环控制仿真波形
t0时刻接触器进入起动过程,电路自动选择励磁状态,电磁吸力于t1时刻迅速增加到参考值,此时磁路磁链也增长到最大值。而后,驱动电路根据设定的滞环宽度自动选择合适的电路状态,使电磁吸力保持动态恒定,线圈电流及磁链则随着闭合过程中动静铁心间气隙的减小而自然减小。由于在动静铁心即将闭合时,磁路电感迅速增大,严重阻碍线圈电流的调节速度,导致电磁吸力出现超调尖峰,但很快又被去磁状态电路自动调节至吸力参考值附近。因为这一超调尖峰的持续时间极短,且作用于动铁心这一质量较大的惯性对象,故对动铁心速度的影响极小。
t2时刻接触器的动静铁心闭合,此时动铁心末速度为1.45 m/s。t3时刻电磁吸力进入稳定的滞环宽度内,此时线圈电流被调节至0.145 A,磁链被调节至1.47 Wb,自动转入节能保持过程。电路仅在续流状态与励磁状态间快速切换,维持吸力动态恒定的同时有效降低了开关管的导通周期数,进一步降低保持功耗。t4时刻进入分断过程,电路自动选择去磁状态进行快速退磁,于t5时刻线圈电流及电磁吸力降为0,t6时刻动铁心回复到分闸位置,分断完成。
在整个动作过程中接触器动态模型输出的电磁吸力与神经网络观测吸力保持一致,证明了观测模型的准确性。对接触器动态过程电磁吸力的准确控制也证明了吸力闭环控制策略的有效性。
设置不同的吸力参考值Fr,进一步利用该仿真系统得到不同参考值下的电磁吸力及动铁心速度数据,并将其共同绘制于图9 中。通过观察动铁心合闸末速度vc的变化可知:随着参考值Fr的增大,动铁心合闸末速度vc也在增大。因此在接触器的直接吸力闭环控制中,设定不同的吸力参考值,即可获取不同的动铁心末速度,在保证接触器可靠起动的同时又可控制动静铁心的撞击能量,从而抑制起动过程中的触头弹跳,方便地进行优化控制。
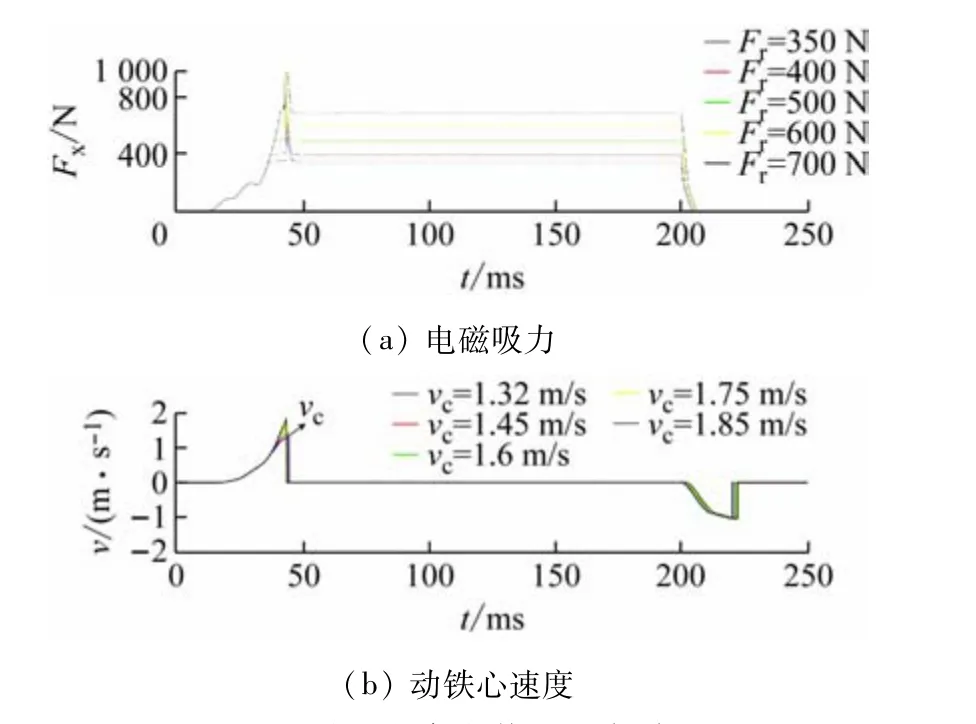
图9 不同吸力参考值下的仿真对比
4 实验分析
4.1 智能电器的快速控制原型验证系统
以NI公司低成本的single-board RIO单板控制器为核心,构建如图10 所示的快速控制原型验证系统,包括:接触器驱动电路、电压电流传感器、激光位置传感器、示波器以及与单板控制器交互的上位机。
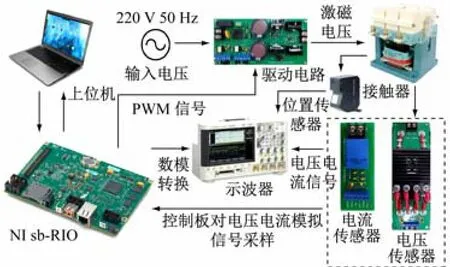
图10 快速控制原型验证系统组成
系统采用LabVIEW 图形化编程语言快速设计直接吸力闭环控制策略,单板控制器包括板载FPGA(Field Programmable Gate Array)模块,具有天然的并行优势及严格确定的程序执行时间,可实现复杂控制算法的高速运行,并与硬件设备实时结合,迅速验证控制方案的可行性。系统具有良好的人机交互界面,便于控制参数的实时调整及运行波形的直观显示,已成为“智能电器”实验教学的高效平台。
4.2 直接吸力闭环控制的实验验证
选取CJ20-630 接触器为控制对象,滞环频率fs设为20 kHz,滞环宽度ε 设为10 N,起动和保持吸力参考值Fr均设为400 N,得到吸力闭环控制下的起动、保持及分断过程实验波形,如图11 所示。
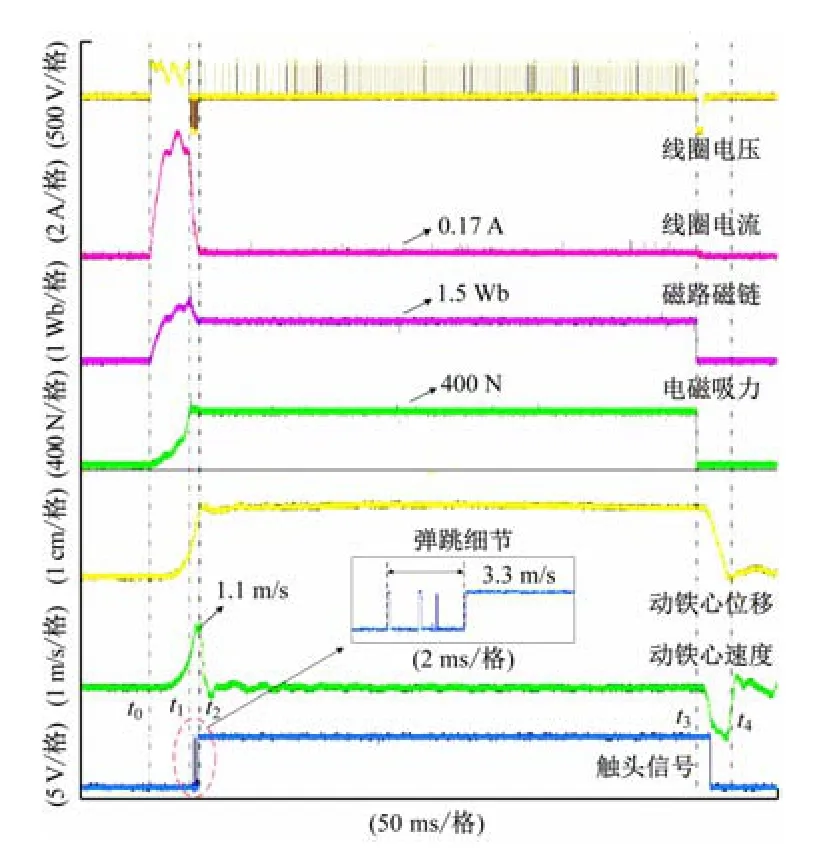
图11 吸力闭环控制实验波形
t0时刻,单板控制器通过板载ADC接口及传感器采集线圈电压、电流信号,并计算得到电磁机构磁链及吸力,计算值一方面用于闭环控制,另一方面通过板载DAC接口输出至示波器,便于观察。在FPGA 中闭环控制策略的作用下,电路自动工作于励磁状态,接触器进入起动过程。电磁吸力快速建立,在t1时刻达到参考值,同时磁链也达到最大值。t2时刻,接触器动静铁心闭合,合闸末速度vc为1.1 m/s,触头弹跳时间为3.3 ms,线圈电流被自然调节至0.17 A,磁链也调节至1.5 Wb,充分体现了吸力闭环控制有效抑制触头弹跳及节能的优势。之后驱动电路仅在激磁状态和续流状态间快速切换,维持电磁吸力在滞环宽度内的动态恒定,进入稳定的节能保持过程。t3时刻,接触器以去磁状态进行快速退磁分断,t4时刻分断结束。完成了接触器直接吸力闭环控制的实验验证。
在实验中,将吸力参考值Fr分别设置为500、600、700 及800 N,起动过程波形如图12 所示,结合图11 可知,随着吸力参考值Fr的增大,接触器自动转入保持过程时的线圈电流也随之增大,合闸末速度vc同样增大,带来了更严重的触头弹跳,与仿真规律一致。因此,实际应用中在保证接触器可靠吸合的前提下,应尽量选取较低吸力值作为参考,可抑制触头弹跳并兼顾节能保持。
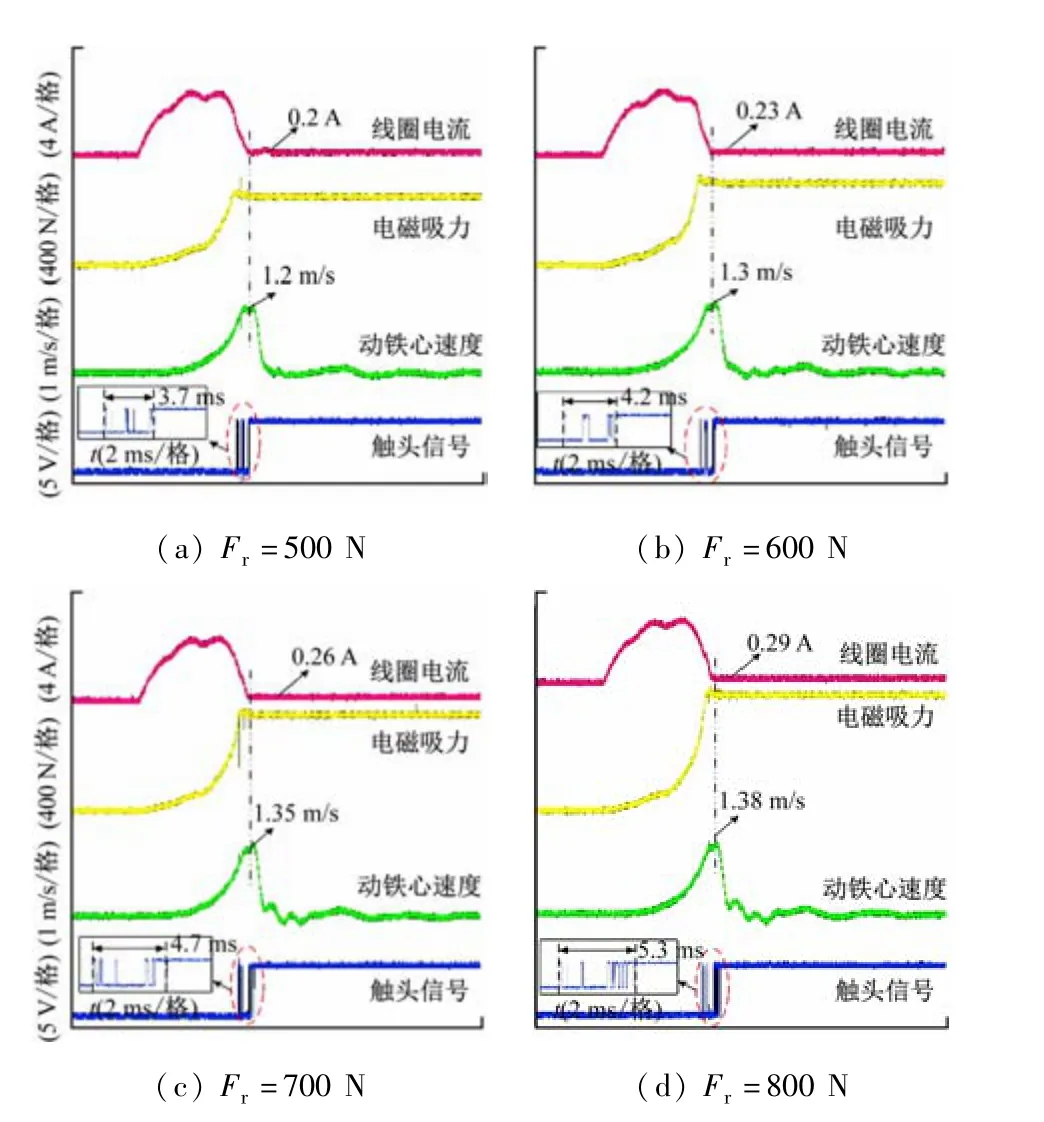
图12 不同吸力参考值下的起动过程波形
5 结语
梳理了经典控制理论、现代控制理论及智能控制理论在电器智能控制中的应用现状,指出目前这些控制理论与电器智能化技术融合时存在的不足,便于学生深入理解已有的自动控制理论与智能电器的融合方法。探索了智能控制理论与智能电器的新型融合方法——引入神经网络构建接触器的电磁吸力实时观测器,在此基础上实现了接触器的直接吸力闭环控制方案。采用联合仿真及快速控制原型验证来直观地呈现控制理论到实际应用的逐步转化过程,有利于激发学生的兴趣,同时加深对智能控制理论的理解,实现理论与实践的融合。

