一种验证双基编队卫星InSAR相位同步MGC正确性的方法研究

赵毅轩,刘爱芳,黄 龙

(中国电子科技集团公司第十四研究所,南京 210039)

0 引 言

数字高程模型(DEM)[1]是带有大地高低起伏的高程信息的三维数字地图,有着十分广泛的军民应用需求。天基干涉合成孔径雷达(InSAR)[2]作为一种大地高程测绘技术,继承了合成孔径雷达(SAR)的全天候、全天时、处理自动化等诸多优点,已发展成获取全球DEM的新型实用遥感系统。已有搭载在编队卫星上的天基InSAR系统在轨运行,如德国的TanDEM-X系统[3-4]和我国的TH-2系统[5],更多的同类系统也在研制中。

对于编队卫星载InSAR系统,相位同步是直接影响系统性能的核心关键技术[5-6],目前普遍采用星间双向交替对传相位同步信号的方式实现[7],其中双星对传的相位同步信号的幅度成为系统关注的重点[8],因为若其幅度过大,会因接收机的限幅而“饱和削顶”,导致接收到的相位同步信号畸变,引出相位同步误差;若幅度过小,则接收到的相位同步信号的信噪比低,导致相位同步精度下降。工程上采用手动增益控制(Manual Gain Control, MGC)技术,通过设置不同的MGC值来调节相位同步信号幅度,使其满足每次工作时的需求。在轨星载InSAR系统中的MGC设置值随卫星注数指令包由地面上注给卫星。

在上述背景下,验证星上的InSAR相位同步MGC是否正确(涉及设置值及其执行是否正确),同时还要满足较高的数据处理时效性,作为一项新的工程实际需求被提出。本文提出一种快速验证星载InSAR系统相位同步MGC正确性的方法,对星载InSAR系统的性能测试以及双星相位同步性能的分析、优化与评估,都有十分重要的意义。

1 相位同步MGC正确性验证方法

本文提出的快速验证星载InSAR系统相位同步MGC正确性方法(流程如图1所示)基于双星相位同步MGC工程经验公式:

(1)

式中,Pop为A/D最佳输入信号功率;Gr为接收通道增益;Pt为相位同步通道的峰值发射功率;λ为雷达中心频率对应的波长;Ls为同步通道系统损耗;φi为相位同步信号发射接收离轴角;G(φi)为离轴角φi处的发射接收天线方向图增益的二次拟合函数;Ri为双星有效基线[8];K为玻尔兹曼常数;T为系统温度;B为接收通道带宽;F为同步通道的系统噪声系数。

图1 快速验证星载InSAR系统相位同步MGC正确性方法流程

重点关注双星InSAR模式工作时实时变量Ri和φi的求解,其中Ri可以通过卫星空间几何位置关系直接计算;可以结合等效思想与矢量投影方法[9]快速计算φi,这样就规避了工程中常见的因多次坐标系转换所产生的大量矩阵运算,因此本文方法的计算量远小于传统坐标转换方法。

1.1 双星有效基线计算

在N个卫星遥测帧中提取出“本星绝对位置”(xa1,ya1,za1),(xa2,ya2,za2),…,(xaN,yaN,zaN)、“它星绝对位置”(xb1,yb1,zb1),(xb2,yb2,zb2),…,(xbN,ybN,zbN)和“本星绝对速度”(vax1,vay1,vaz1), (vax2,vay2,vaz2),…, (vaxN,vayN,vazN)。

定义“双星相对位置”为(xr1,yr1,zr1), (xr2,yr2,zr2),…,(xrN,yrN,zrN),其中xri、yri、zri为地固坐标系下“双星绝对位置”坐标的差值,即

xri=xbi-xai

(2)

yri=ybi-yai

(3)

zri=zbi-zai

(4)

在双星InSAR模式N帧成像期间,有

(5)

提取出双星有效基线为R1,R2, …,RN。

1.2 相位同步信号发射接收离轴角快速计算

SAR载荷在卫星本体B坐标系下同步天线喇叭法线指向为(xB,yB,zB),利用下式将其转换到卫星Hill坐标系:

(xH,yH,zH)=A-1*B-1*(xB,yB,zB)

(6)

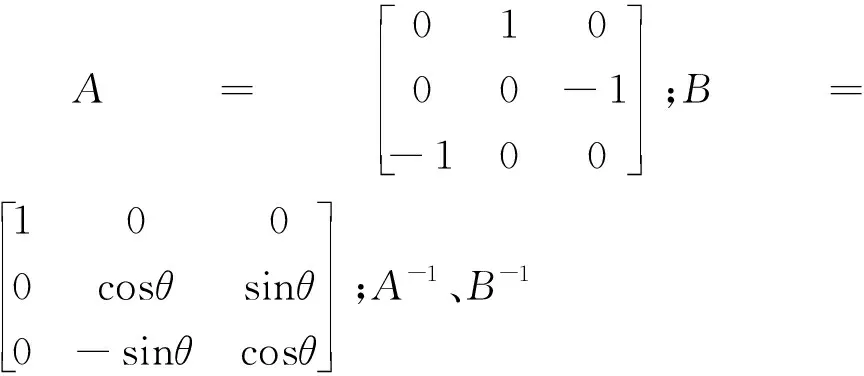
提取出同步天线喇叭法线朝向在Hill坐标系下的坐标(xH,yH,zH)。

本星向它星发射相位同步信号的指向与本星向它星的有效基线连线方向相同,即等效成将“双星相对位置”由地固坐标系坐标(xr1,yr1,zr1),(xr2,yr2,zr2),…,(xrN,yrN,zrN)转换成Hill坐标系下坐标(xHr1,yHr1,zHr1), (xHr2,yHr2,zHr2), …,(xHrN,yHrN,zHrN)。

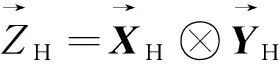
(7)

求解出卫星Hill坐标系z轴正方向为

(8)

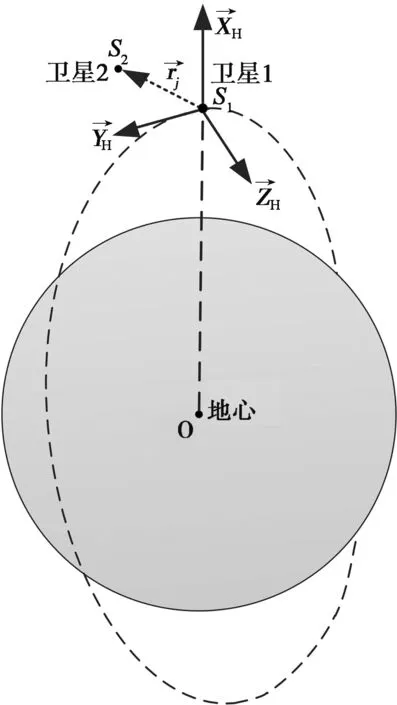
图2 双星相对位置矢量与Hill坐标系关系

已知矢量投影公式

(9)

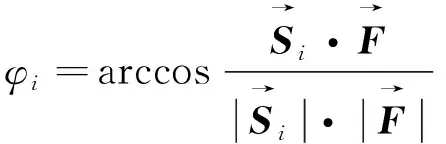
(10)

即提取出相位同步信号发射接收离轴角φ1,φ2,...,φN。

1.3 相位同步MGC理论实时值计算

式(1)中的G(φi)使用二次函数拟合:

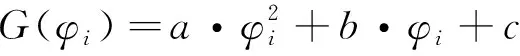
(11)

式中,a、b、c均为二次拟合参数。

式(1)转化为分贝表示:

MGCdBi=10lg(MGCi)

(12)

将双星有效基线为R1,R2,...,RN与相位同步信号发射接收离轴角φ1,φ2,...,φN代入式(12),求解双星InSAR成像工作期间相位同步MGC的理论实时值MGCdB1,MGCdB2,...,MGCdBN。

1.4 相位同步信号功率计算

计算相位同步信号s1,s2,...,sM的功率谱为S1,S2,...,SM,对功率谱S1,S2,...,SM在相位同步信号带宽内求均值,提取出相位同步信号功率P1,P2,...,PN。

1.5 相位同步MGC设置值正确性验证

对上述提取出的相位同步MGC理论实时值MGCdB1,MGCdB2,...,MGCdBN寻找最大值MGCdBMAX,进行阈值判定:

ε0>|MGC0-MGCdBMAX|

(13)

式中,ε0为卫星推演轨道偏差对计算MGC设置值的最大误差;MGC0为星上MGC设置值;ε0、MGC0均由地面运控系统提供。

若式(13)成立,则验证星上相位同步信号MGC设置值正确。

1.6 相位同步MGC执行正确性验证

SAR载荷按照MGC理论实时值执行相位同步所对应的相位同步信号的理论功率为

Gi=Pi+MGC0-MGCdBi

(14)

式中,Pi为相位同步信号功率;MGC0为星上MGC设置值;MGCdBi为MGC理论实时值。

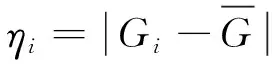
(15)

得到G1,G2,...,GN的误差η1,η2,...,ηN。

SAR载荷相位同步信号MGC的系统误差ε1是个常数。阈值判断:

ηi<ε1

(16)

若式(16)成立,则验证星上相位同步MGC执行正确。

2 仿真验证

为验证上述方法的有效性与可行性,模拟双基编队卫星遥感数据、下行的同步信号数据以及SAR载荷系统工作参数,开展仿真试验,试验流程与第1章方法一致。仿真实验输入系统参数如表1所示。

表1 输入系统参数

依据模拟卫星遥感数据“本星绝对位置”、“它星绝对位置”与“本星绝对速度”,计算双星的模拟有效基线由241.7 m向244.9 m呈非线性变化,如图3所示。

提取同步天线喇叭法线的指向在卫星Hill坐标系下的坐标,利用等效思想和矢量投影法,提取本星向它星发射同步信号的指向在卫星Hill坐标系下的坐标,快速计算出同步信号发射接收离轴角变化曲线。模拟的双星同步信号发射接收离轴角由43.2°线性变化为47.6°,如图4所示。

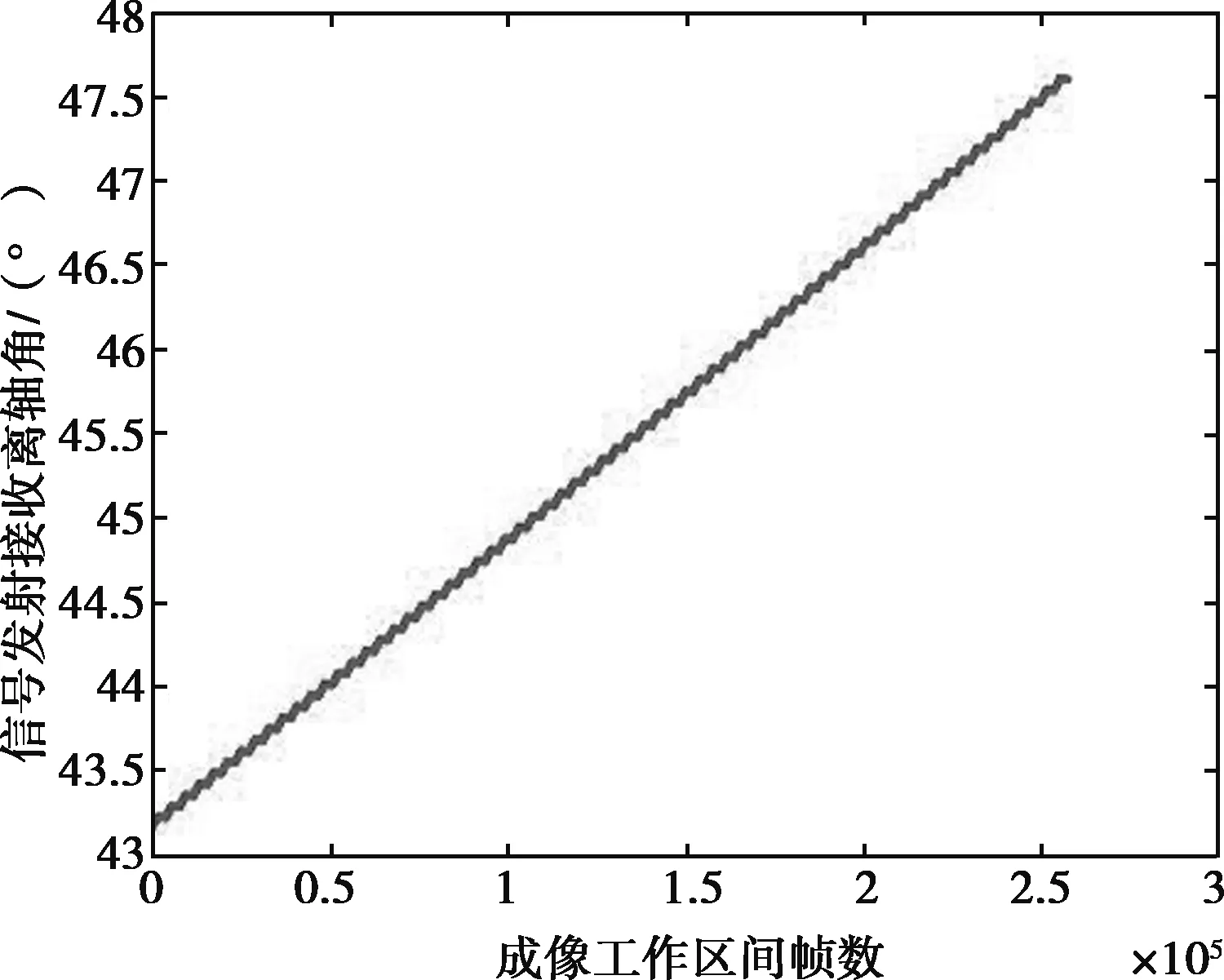
图4 模拟双星同步信号发射接收离轴角实时变化曲线

将模拟双星有效基线、模拟同步信号发射接收离轴角代入式(1)、(11)、(12),求解相位同步MGC的模拟理论值变化曲线。MGC的模拟理论值由23.9 dB线性变化为20.7 dB,如图5所示。

图5 相位同步信号MGC的理论实时变化曲线

模拟相位同步信号带宽内功率由78.9 dBm线性变化为76.0 dBm,变化趋势如图6所示。

对上述提取出MGC模拟理论值MGCdB1, MGCdB2,…,MGCdBN寻找最大值MGCdBMAX=23.9 dB,模拟地面运控系统提供的卫星推演轨道偏差对计算MGC设置值的误差ε0=0.21 dB,模拟星上MGC设置值MGC0=24 dB,满足式(13),即本次仿真相位同步MGC设置值是正确的。

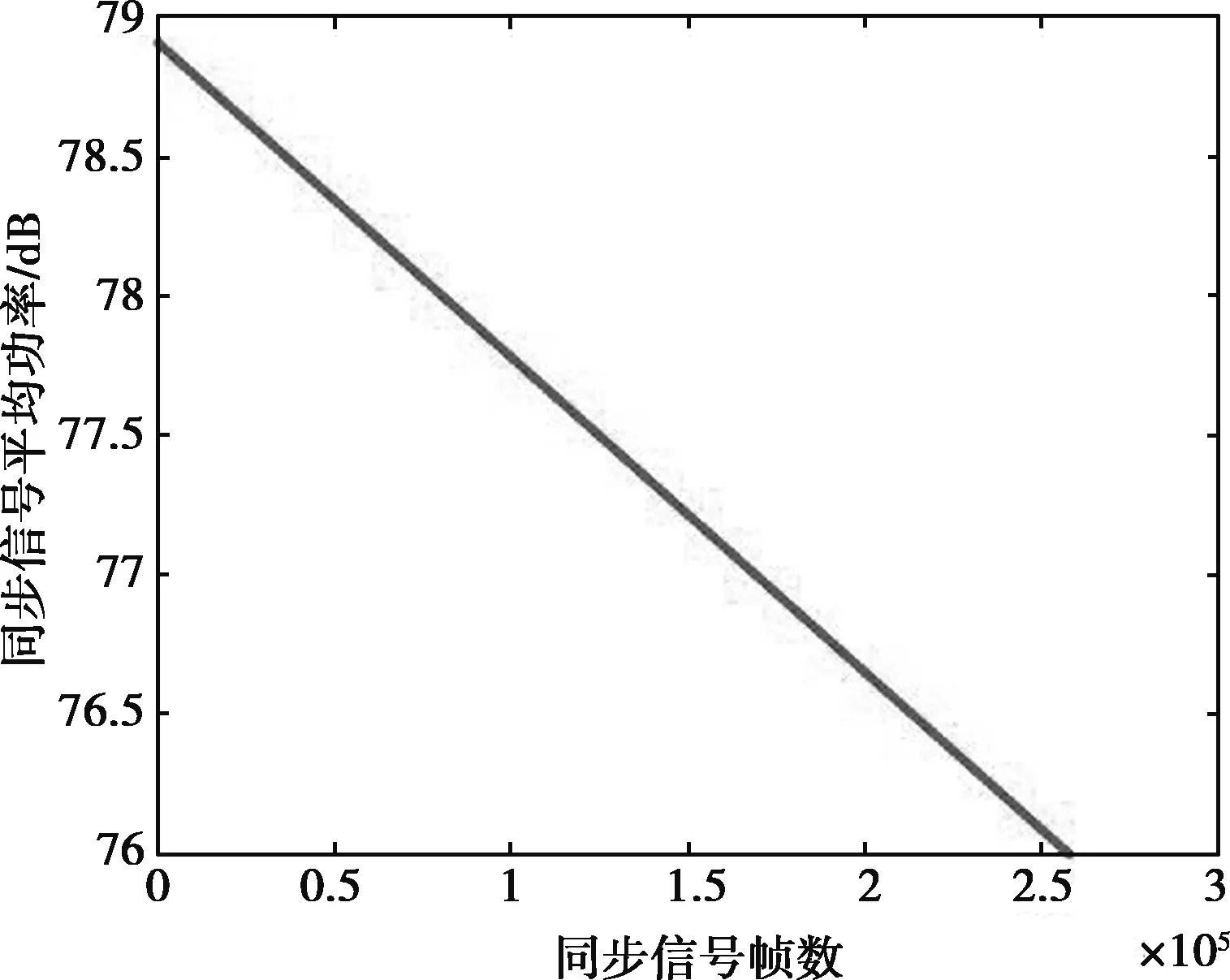
图6 相位同步信号带宽内功率曲线

将模拟相位同步信号功率、模拟星上MGC设置值、MGC模拟理论值代入式(14),得出模拟相位同步信号的理论功率曲线如图7所示。

图7 相位同步信号理论功率曲线

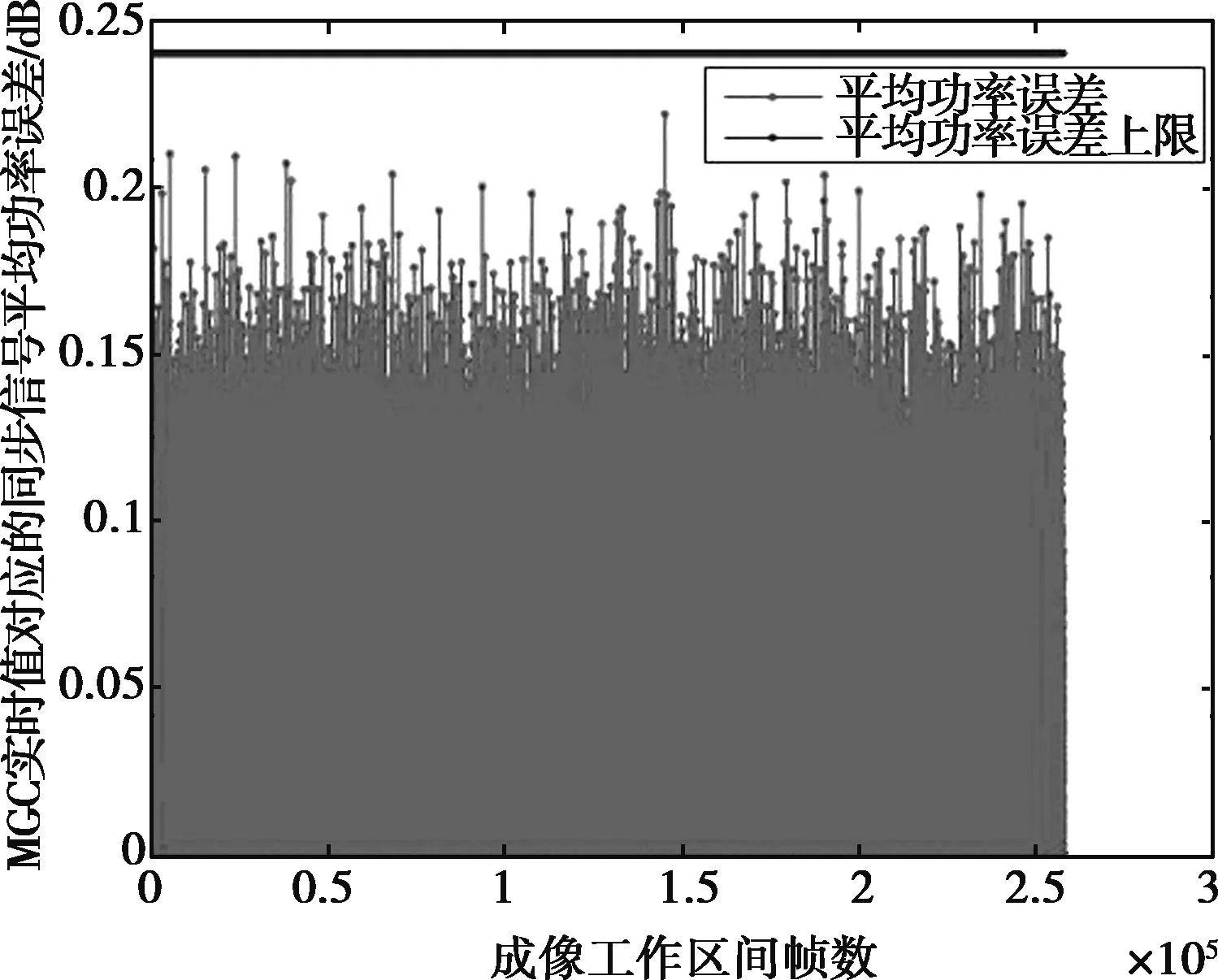
图8 相位同步信号理论功率误差曲线

3 结束语

本文方法适用于星载、机载InSAR系统以及相似原理系统的相位同步MGC正确性验证。通过利用卫星遥测数据、下行的同步信号数据,可以解决双星无法验证InSAR星上同步信号MGC正确性与稳定性的工程实际问题。同时,利用等效思想与矢量投影法相结合,巧妙快速计算同步信号发射接收的离轴角,相较于工程中常见的坐标系转换算法,减少了运算量,提高了算法的时效性。