直流受端电网暂态稳定协调优化控制方法
章玉杰,祁中建,单 哲,李卫平,任延春,史 阳
(国网江苏省电力有限公司超高压分公司,江苏 南京 211100)
0 引言
“双碳”目标下中国西部地区丰富的风电和水电资源开发规模及消纳需求日益增加[1-2],东部负荷中心区外受电比例不断增大[3-5],超/特高压直流输电成为远距离跨区大容量输电的主要手段[6-7]。直流闭锁等故障可引发暂态频率和电压稳定问题[8-10]。
文献[11]在分析频率稳定问题原因和现有稳控技术的基础上构建了一套包含直流功率提升、抽蓄切泵以及切除负荷等控制手段的频率稳定协调控制系统并实际应用于华东电网(华东频率协控系统)。在此基础上,文献[12]详细分析了馈入受端电网的直流功率提升原理,考虑系统安全约束、计及区域电网支撑能力,提出了一种直流闭锁故障导致受端系统大功率缺额后多直流功率紧急提升协调控制技术。此外,对于直流闭锁故障后电网暂态电压稳定问题,文献[13]综合考虑机组有功出力、直流功率和机端电压等控制手段,以暂态电压恢复指标为目标,提出一种暂态电压稳定优化控制模型。
暂态稳定控制时所采取切负荷控制会对社会经济造成一定的影响,此外,频率、电压等稳控措施也会存在不同程度设备、人力、时间上的控制代价。随着新型电力系统的发展,越来越多的市场主体参与电网调频和稳定控制辅助服务,兼顾电网运行安全性和经济性成为新形势下研究的热点[14-16]。文献[14]兼顾直流闭锁故障后系统大功率缺额造成的频率和电压暂态稳定问题,以总切负荷控制代价最小为目标,采用轨迹灵敏度线性化稳定约束,建立了优化切负荷控制模型,求解非线性问题。进一步地,文献[15]以紧急切除负荷控制代价最小为目标,同时考虑故障后系统暂态功角、频率、电压稳定约束,建立了紧急切负荷控制优化模型。文献[16]进一步利用电网新一代调相机控制资源[17],同时计及系统频率和电压暂态稳定性两个方面因素,提出一种以总控制成本最小为目标、考虑直流功率提升、调相机强励磁控制和切负荷等多控制方法的协调控制优化模型,基于轨迹灵敏度方法线性化约束条件进行迭代求解。交流滤波器既能滤除谐波,也能为换流器提供无功功率[18-19],可作为协调控制资源参与近区电网故障时暂态电压稳定紧急提升控制。此外,上述方法采用轨迹灵敏度法计算多个控制变量灵敏度时需进行多次串行时域仿真,计算耗时较长、效率较低。
综上,本文进一步挖掘非故障直流受端换流站近区交流滤波器控制资源,提出一种采用直流功率提升、交流滤波器投切、调相机强励磁以及切除负荷的优化控制方法。考虑直流提升有功功率与交流滤波器无功功率联锁,引入设备运维人力成本表征控制变量单位控制成本,以不同权重系数区分各类型控制手段控制差异;以最小控制成本为目标,建立直流受端电网暂态频率和电压稳定协调优化控制模型。基于VC++和多线程技术实现模型求解与控制变量灵敏度并行计算。最后以华东电网的实际算例仿真分析,验证了本文协调控制策略有效性,可有效提高直流闭锁故障后受端电网的暂态频率和电压稳定性,适合在线应用。
1 多控制手段优化控制模型
以最小控制成本为目标,以直流有功功率提升量、调相机励磁电流增量、切负荷量、换流站交流滤波器无功功率投切量为控制变量,建立优化模型如下。
式(1)中,J为总控制成本;ξD、ξS、ξC、ξL分别为直流有功功率提升量、调相机强励磁电流增量、交流滤波器无功功率投切量以及切负荷量控制权重系数;ND、NS、NL分别为各类控制手段参与控制变量数;λDi、λSi、λCi、λLi为各类控制手段第i个控制变量成本系数;ΔPD、ΔIS、ΔQC、ΔPL分别为各类手段控制变量向量;ΔPDi、ΔISi、ΔPLi、ΔQCi为各类控制手段第i个控制变量。
式(2)、式(3)分别为暂态频率和电压稳定裕度约束,Rf0和Rv0为暂态频率和电压稳定裕度初值,Rfset和Rvset为暂态频率和电压稳定裕度设定门槛值,SfD、SfC、SfS、SfL和SvD、SvC、SvS、SvL分别为暂态频率和电压稳定裕度对各控制变量灵敏度向量。
式(4)、式(5)、式(6)、式(7)分别为各类型控制变量向量与上下限值向量约束,PDmax、PLmax、ISmax、QCmax分别为4种类型控制变量上限值向量。
式(8)为直流功率提升和切负荷总量与直流闭锁导致的有功功率损失量约束,ΔPset为直流闭锁故障导致的系统有功功率损失量。
式(9)为直流有功功率控制第i个变量有功功率与交流滤波器无功功率投切量约束,其中Qmin为第i个直流在初值PD0,i下提升ΔPDi有功功率所需的最少滤波器无功功率,QC0,i和ΔQCi分别为第i个直流控制变量对应的无功功率初值和交流滤波器无功功率控制量。
2 控制策略求解与并行计算
2.1 直流功率与滤波器约束处理
直流逆变换流站投入交流滤波器无功功率与直流有功功率存在联锁且按组投切,其无功功率呈分段阶跃特性,可用下式所示分段函数进行描述。
式(10)中,Mi、Ni、Ki分别为第i个参与协调控制直流有功功率P处于不同功率水平(Pi1、Pi2、Pi3、Pi4)时所需的最少滤波器无功功率Qmin,i。
进一步,对式(10)分段函数作单一化处理成式(11),约束条件(9)中Qmin可用式(11)计算。
2.2 控制策略求解流程
多控制手段暂态稳定协调优化控制策略求解流程如图1所示,详细步骤如下。
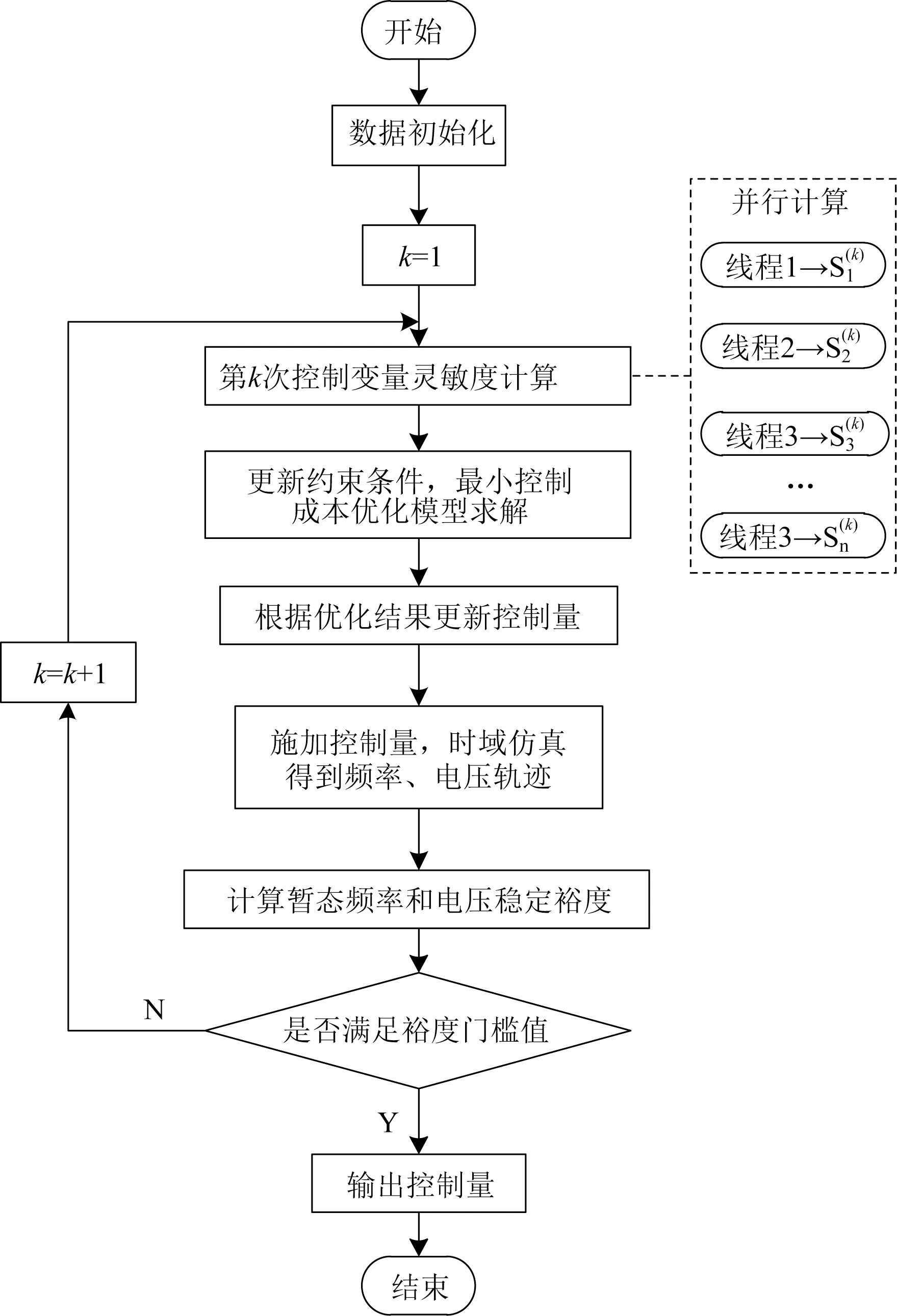
图1 优化控制策略流程图Fig.1 Flow chart of control strategy optimization
步骤1:初始化各数据及参数,根据预想故障设置仿真步长和时长、参与控制变量初值、上下限值、暂态频率和电压稳定裕度二元表[16]、暂态稳定门槛值等参数。按式(11)预处理式(9)约束条件。控制成本系数和权重系数通过电网运行经验和设备运维成本进行设定,以尽可能满足工程应用要求。
步骤2:基于BPA时域仿真软件,采用并行算法计算第k次优化后各控制变量灵敏度[14]。直流功率控制量增量和切负荷控制量增量摄动值取10 MW,滤波器按组投切、变量摄动量取小组滤波器无功容量(如190 Mvar),调相机强励磁控制变量摄动量取0.1 p.u.(励磁电流)。
步骤3:更新优化模型约束条件(式(2)、式(3)),求解优化模型(式(1)-式(9))得到使总控制成本最小目标下的各控制变量值。
步骤5:基于当前方式,施加控制量进行时域仿真得到频率、电压响应轨迹。
步骤6:根据采取控制量后的频率、电压响应轨迹计算系统暂态稳定裕度,判断是否满足设定门槛值,若满足则结束优化计算,否则继续优化。
2.3 轨迹灵敏度并行计算
利用摄动法求取灵敏度需对各控制变量分别施加摄动量并进行时域仿真,各时域仿真过程相互独立,可通过多线程并行技术加快计算速度[20-24]。此外,PSDBPA潮流和稳定程序(pfnt.exe、swnt.exe)仅支持单个进程串行运行,无法同时对多个输入文件(控制变量摄动量后的swi稳定文件)进行仿真。本文设计了如图2所示的并行算法逻辑,按控制变量数量配置并行线程数,每条线程配置独立的BPA程序镜像,独立完成单个控制变量摄动量时域仿真、稳定裕度指标计算、灵敏度计算,各线程相互独立、并行完成并同步计算结果。

图2 控制变量灵敏度并行计算算法Fig.2 Parallel computation algorithm for variable sensitivity control
单条线程基于第k次优化施加控制量后系统频率、电压轨迹,计算稳定裕度R(xi)(k),对第i个控制变量xi施加摄动量Δxi,自动填写相应LS故障控制卡并生成BPA 稳定文件(sw_x*.swi),调用BPA 稳定程序swnt_i.exe进行时域仿真,得到频率、电压响应轨迹,计算施加摄动量控制量后的系统暂态稳定裕度,进一步计算得到控制变量灵敏度[25]。
3 算例分析
以多直流馈入的华东电网为例,对本文优化控制方法进行验证。采用PSD-BPA 时域仿真软件,基于VC++2022环境配置Cplex12.6优化求解器对优化模型进行求解,整体控制策略求解基于VC++多线程技术编程实现。设置BPA 软件仿真步长0.01 s、仿真时长15 s。设定暂态频率稳定二元表为(49.7 Hz,0.5 s)和(49.75 Hz,1 s),暂态电压稳定二元表为(0.75 p.u.,1 s)和(0.7 p.u.,0.1 s)。
华东电网某运行方式下电网总负荷为306.95 GW,区外直流总受电量为63.35 GW,占负荷总量的20.6%,电网总旋转备用量为8.26 GW,旋转备用率为2.69%。设置锦苏直流0.1 s时双极闭锁故障,故障前双极功率为7 200 MW,0.2 s时整流侧和逆变侧换流站交流滤波器和并联电容器组自动全部退出运行。故障后受端换流站近区500 kV 母线“苏吴江_525”电压最低跌至0.795 9 p.u.,暂态电压稳定裕度为0.531 5;系统频率最低跌至49.753 5 Hz(10.5 kV 发电机母线:苏平燃_4),暂态频率稳定裕度为0.414 3。根据低频减载装置临界动作频率电压响应设定暂态频率稳定和暂态电压稳定门槛值为0.73和0.83。
应用本文协调控制策略进行优化计算,选取控制集为:非故障直流功率(龙政直流、雁淮直流、林枫直流)、受端换流站交流滤波器(沪政平_50、苏南京_50、沪枫泾_50),锦苏直流受端换流站调相机(华苏调_122、华苏调_222)、龙政直流受端换流站调相机(华政调_122、华政调_222、华政调_322、华政调_422)以及雁淮直流受端换流站调相机(华晋调_122、华晋调_222),锦苏直流受端换流站一级送出断面以及近区分区负荷(吴江、车坊、木渎、玉山)。各控制变量初始值、控制量上限、成本系数、权重系数等信息如表1所示。

表1 参与协调控制各控制变量Table 1 Variables for coordination control
优化计算过程中,各控制变量、总控制成本和暂态稳定裕度变化情况分别如表2、表3所示。第1次优化时,由于直流功率提升控制优先级较高以及直流功率与滤波器投切联锁,直流功率和滤波器无功控制量全部投入,后续优化过程中保持上限值。直流提升功率达上限值后,需要切除吴江分区和车坊分区部分负荷以提高系统暂态频率稳定裕度。同时,苏州站(华_苏调)和政平站(华_政调)部分调相机提高强励磁电流,优化后系统暂态频率和电压稳定裕度有效提升,总控制成本显著增加。
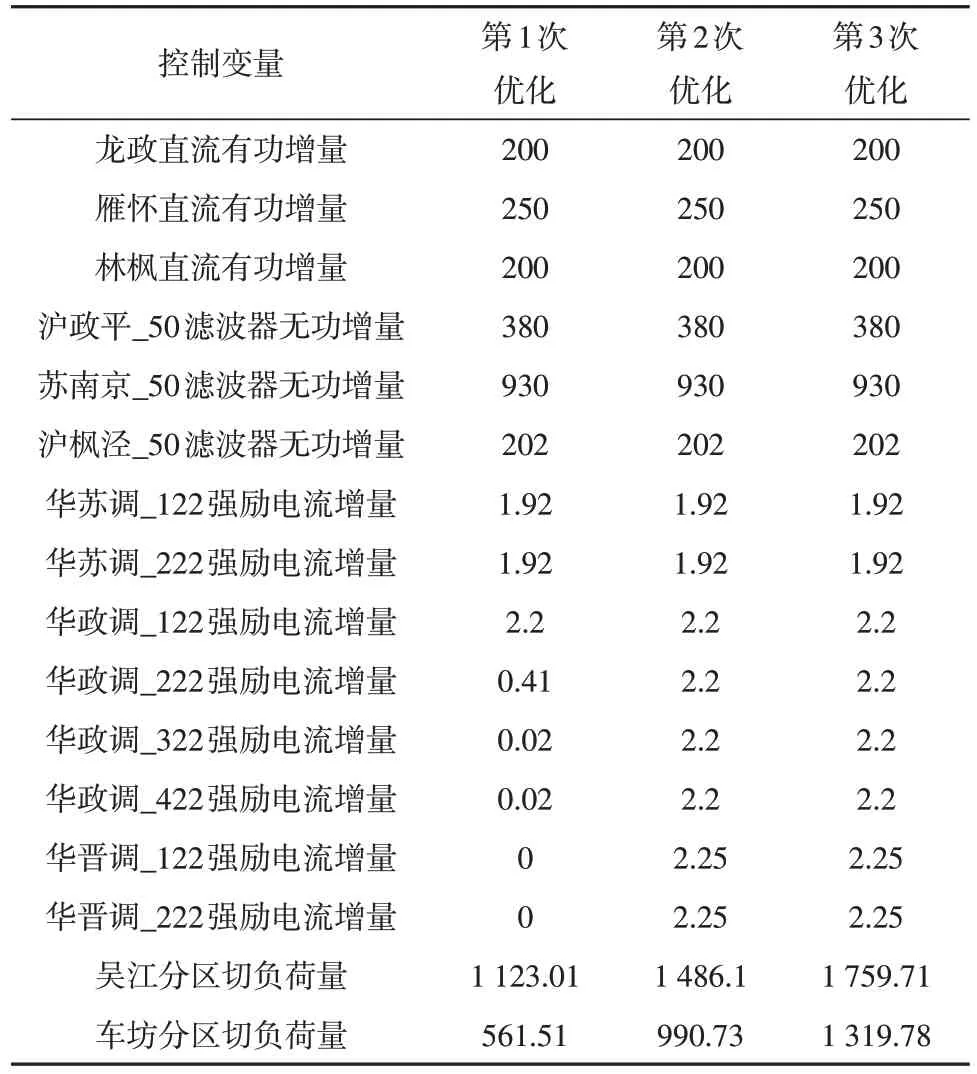
表2 优化计算过程中各控制量变化情况Table 2 Changes of control variables during optimization calculation
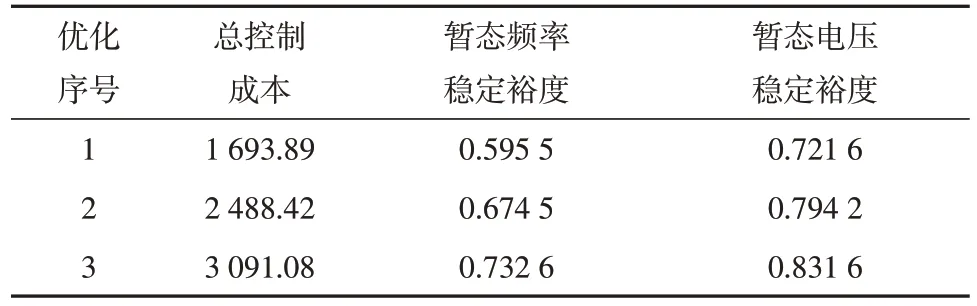
表3 优化计算过程中各参数变化情况Table 3 Variations of parameters during optimization calculation
第2 次优化时,参与协调控制的全部调相机提升强励电流至上限值(3.5 p.u.),系统暂态电压稳定裕度得到提升且接近设定值0.8,进一步通过切除负荷提高暂态频率稳定裕度。第3 次优化时,增加吴江分区和车坊分区切负荷量,进一步提升系统频率和电压稳定裕度,均达到预设门槛值,优化结束,得到暂态频率和暂态电压稳定协调控制策略。
应用优化得到的控制策略故障后0.15 s对电网进行暂态稳定控制,直流有功功率提升、调相机强励磁电流提升、切负荷、交流滤波器无功功率投切控制结束时间分别为故障后0.2 s、0.5 s、0.3 s、0.2 s,仿真试验表明上述控制时序可满足稳控要求[11]。
从表3 可以看出,施加控制策略后电网频率和电压稳定裕度显著提高。控制前后电网频率、电压曲线(取前2 s暂态过程)如图3、图4所示,随着施加控制量的增加,系统暂态频率和电压稳定水平也明显逐步提升。
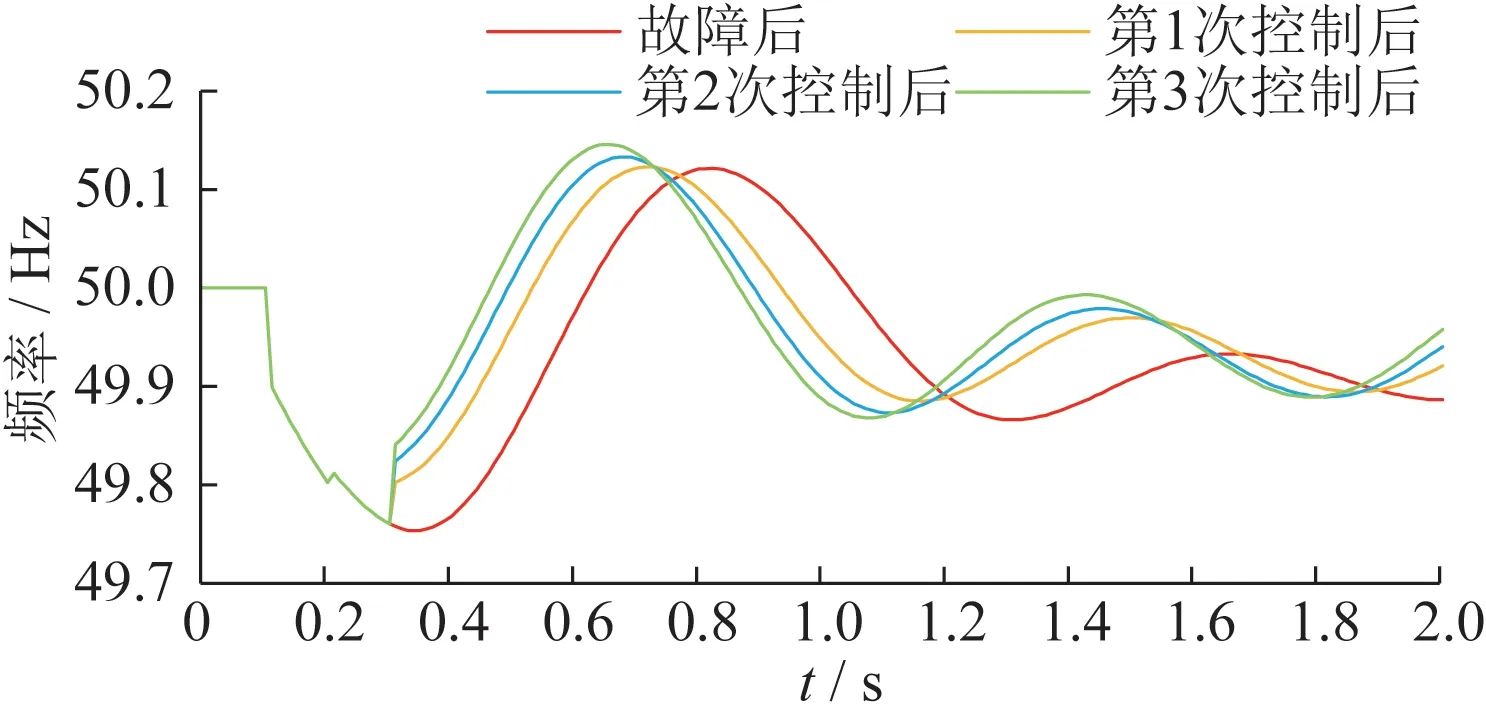
图3 控制前后系统暂态频率曲线Fig.3 Transient frequency curve of the system before and after control
仅考虑单一切负荷控制和采用协调控制策略下切负荷量如表4 所示。通过对比,采取本文协调控制策略比单一切负荷控制减少676.7 MW切负荷量。龙政、雁淮、林枫直流有功功率每提升100 MW 将分别降低系统暂态电压稳定裕度0.000 264、0.000 104 和0.000 16。以车坊分区电压稳定裕度切负荷控制灵敏度折算,协调控制提升非故障直流功率650 MW,降低系统电压稳定裕度0.011 08,约造成184.67 MW额外切负荷量。值得注意的是,参与协调控制直流功率提升受端换流站交流滤波器投入1 512 Mvar 无功功率,将系统暂态电压稳定裕度提升0.017 052,不仅补偿了直流功率提升对系统暂态电压稳定带来的负效应,还减少284.2 MW切负荷量。
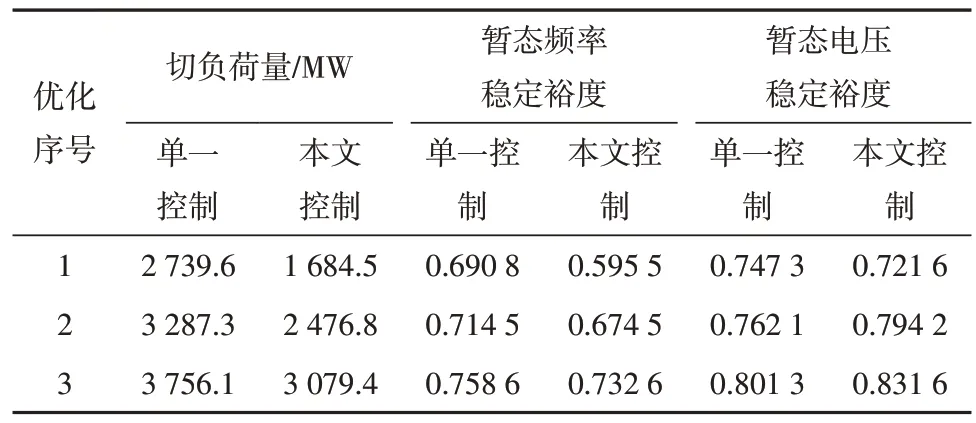
表4 单一控制与协调控制下切负荷量对比Table 4 Comparison of load shedding under single and coordinated control
本文协调控制策略求解所使用的计算机硬件配置为Intel Core i7-10700F处理器、主频2.9 GHz、16 GB内存。总优化求解时长15.876 s,其中并行时域仿真固有时长15 s,灵敏度计算和优化模型求解时长876 ms,满足电网稳控策略“在线预算,实时匹配”应用要求。
4 结语
随着多直流馈入电网区外受电比例越来越大,在发生大容量直流闭锁故障后,电网暂态稳定性问题突出。本文充分考虑直流功率提升、交流滤波器投切、调相机强励磁和切负荷等控制手段,以最小控制成本为目标,建立优化控制模型。进一步考虑了换流站交流滤波器无功控制资源并计及与直流提升有功功率的约束,基于轨迹灵敏度方法设计实现了暂态频率与电压稳定协调优化控制策略并求解。对华东电网进行算例分析,验证了本文协调控制方法的有效性。如何进一步协调故障后受端电网各类无功控制资源参与暂态频率、电压稳定协调控制将是下一步研究方向。

