基于萤火虫算法与BP神经网络的电力系统短期负荷预测
朱婉婷,何郭顺,陶劲松*
(1.武汉大学数学与统计学院, 湖北 武汉 430072;2.武汉大学电气与自动化学院, 湖北 武汉 430072)
0 引言
随着社会经济的不断发展,人民生活对于供电的要求越发严格,加之新能源大量并网导致供电波动的时代背景,社会生产生活对于短期电力负荷预测的准确性提出愈发高的要求。
目前,大量的研究工作聚焦于以神经网络为主题进行方法优化使得预测结果更加精确,如文献[1]基于BP 神经网络算法进行预测,并使用遗传算法对BP 神经网络的初始权值和阈值进行优化;文献[2]将ECA模块应用于时间卷积神经网络中,有效提升CNN 性能;文献[3]将小波分解、小波重构与粒子群算法引入BP神经网络,增强了信息的有效性。上述文献均有其特定的适用空间,但由于负荷预测过程基于生产实际,具有不确定性,故而难以适用于所有场景。基于此,一些脱离神经网络的预测方法被提出,如文献[4]提出VMD分形理论的算法进行预测,并使用重标极差法对时间序列的预测性进行分析;文献[5]通过小波聚类的方式处理负荷预测中数据反常化的问题,使得负荷预测曲线更加平滑;文献[6]运用最小二乘拟合,解决了预测时刻的影响因素大于学习过程中数据来源的相应影响因素,从而出现归一化负荷预测结果偏差严重问题;文献[7]运用自适应矩阵估计,提升了算法的学习能力;文献[8]引入卡尔曼滤波的方法,解决了因样本容量较少而较难进行预测的节假日电力负荷问题;文献[9]基于IT2FLS 提出电力系统短期预测模型,并采用IT1FLS 和基于IT2FLS 的预测算法实现了电力系统混沌时间序列和短期负荷的高精度预测;文献[10]应用了递归LSTM神经网络对波兰中部小区域电力系统进行短期负荷预测,在预测时间序列的不规则趋势上有一定成果;文献[11]应用基于LM的ANN技术,精确预测智能电网的短期用电负荷,完善发电与利用方面的平衡问题;文献[12]运用实施预测数据和信息来构建数据挖掘电力预测模型,涉及多阶段预测过程,并在整个过程中利用数据挖掘进行修正,得到预测残差,能高精度完成预测任务;文献[13]创新性地提出了将24 h 负荷预测输出分为几组,然后利用多粒子群优化和最小二乘支持向量机相结合的预测方法,并改进算法进行预测,得到精确的预测结果;文献[14]结合完全继承经验模态分解自适应噪声法-模糊熵和改进麻雀搜索算法优化光梯度提升机提出一种短期负荷预测方法,解决了因电力负荷非稳定性强导致的预测精度低的问题;文献[15]通过贝叶斯优化、网格搜索和随即搜索调整超参数来减少MSE,以达到更好的预测效果。上述方法均在特定情形下能够实现较好的预测效果,但是都较少考虑特定影响因子(如温度、湿度)异常而造成的影响。
对于特定影响因素,也有相应研究提出方法对其影响进行分析以达成更优预测结果,如文献[16]将果蝇优化算法引入广义回归神经网络,在引入温度、气象、日期类型等诸多相关性因素的情形下,优化了算法预测的性能与稳定性,但果蝇算法的缺点显著,即对于数据样本容量具有较大要求,而对于异常的气温湿度数据,在实际生产过程中难以获得足够的样本;文献[17]将交互信息理论运用于人工神经网络中,使得预测结果与其他变量的相关性得到充分的考量,但交互信息理论的实操步骤与学习过程都相对繁琐,在生产实践中较难应用;文献[18]应用多时空尺度时间卷积网络模型,减小气候、日程等随机性的影响,简化了数据处理过程,可该方法问题在于,为了提高模型精度往往采用加深模型深度与宽度,这意味着需要海量的数据,当标注数据不足时容易产生过拟合,即便数据充足也会带来巨大的计算压力;文献[19]着眼于研究气候模式和城市微气象对电力负荷产生的影响,可研究变量过少,不具备负荷预测的普适性。本文在数据预处理方面创新点在于,在数据预处理方式中,主成分分析可以较好满足电力系统短期负荷预测的数据处理要求,通过主成分分析,可以计算出多重因素对于负荷预测结果的影响权重,通过线性组合的方式,使得相关因素数据的使用更具有效力,提升负荷预测的准确性。
此外,文献[20]虽不进行电力系统负荷预测方面的研究,但其提出的应用DA-CNNGRU 混合神经网络对输入矩阵时空特性提取能力和预测结果稳定性均有明显提升。
基于以上考虑,本文提出使用主成分分析进行数据预处理,将萤火虫算法与BP 神经网络结合的方式,运用主成分分析的方法确定变量因素对于预测结果的影响程度,进而使用BP 神经网络进行学习与预测,达到更加准确的预测效果。
1 数据预处理与方法概述
本节主要介绍数据预处理和本文的方法,经过处理之后,原始的数据能降低计算维度,减少计算成本,并且保留反映数据本质的特征维度,为后续分析提供了途径。
1.1 数据预处理
用电负荷数据选取中国山东省某市2019年-2022年每年的1月1日-1月31日,按天间隔采集,以控制数据的精度以及不同月份气温带来的影响。由于数据量较大,影响因素较多,故运用主成分分析以降低计算数据的维度,达到使模型更加简洁的目的,主成分分析的数据预处理步骤主要如下[21]。
设有m条n维数据
1) 将原始数据按列组成n行m列矩阵X;
2) 将X的每一行进行零均值化,即减去这一行的均值;

4) 求出协方差矩阵的特征值及对应的特征向量;
5) 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P;
6)Y=PX即为降维到k维后的数据。
本文选取的影响因素为:历史最高最低温度、平均湿度以及当地人均生产总值。最后处理之后,最高温度因素的贡献值达到了87.23%,超出其他因素的贡献值,可以得出结论:温度是最大的影响因素。
1.2 基本理论
对处理过后的数据进行分析,可以得到一些影响负荷趋势的特征和因素,而通过主成分分析可以得到各种因素的贡献值大小,由此判断其与电力负荷的相关性。以下将详细介绍萤火虫算法(Firefly Algorithm,简称“FA”)与BP 神经网络(back propagation neural network)的结构。
1.2.1 萤火虫算法
算法基本思想描述如下:在群体中,将多个萤火虫个体随机分布在目标函数定义的空间中,初始阶段,所有的萤火虫都具有相同的荧光素值和动态决策半径。其中,每个萤火虫个体根据来自动态决策半径内所有邻居萤火虫信号的强弱来决定其移动的方向。萤火虫的动态决策半径会随着在它范围内萤火虫个体的数目而变化,每个萤火虫的荧光素也会随着决策半径内萤火虫个体的数目而改变。萤火虫群优化算法是无记忆的,无需目标函数的全局信息和梯度信息,具有计算速度快、调节参数少、易于实现等特点。萤火虫进化过程中,每次迭代都由萤火虫的部署(初始化)、荧光素更新阶段、移动概率计算阶段、位置更新阶段、领域范围更新阶段5个部分组成:
1) 萤火虫的部署
在可行域中随机放置n个萤火虫,并赋予每个萤火虫的荧光素为l0,动态决策域为r0,初始步长为s,领域阈值为nt,荧光素挥发因子为ρ,荧光素更新因子(适应度提取比例)为γ,动态决策域更新率(领域变化率)为β,萤火虫感知域为rs,迭代次数为M。
2) 荧光素更新阶段
每个萤火虫个体的荧光素值等于前一时刻的荧光素值加上萤火虫当前适应度值的一定提取比例,然后再减去随着时间挥发掉的一定比例的荧光素值,得式(1)。
式(1)中,li(t)为t次迭代时的荧光素浓度大小,ρ为荧光素挥发系数,γ为适应度提取比例,J(xi(t))表示节点i在t次迭代中的适应度值即目标函数值。
3) 移动概率计算阶段
每个萤火虫在具体的移动中,需要根据其决策半径内的所有邻居萤火虫的荧光素浓度大小来决定其移动方向,Pij(t)表示t时刻(迭代次数)第i只萤火虫向第j只邻居萤火虫个体进行移动的概率,计算公式如式(2)。

4) 位置更新阶段
选择最大的移动概率并进行位置更新:萤火虫i朝向它决策半径内具有最大荧光素的萤火虫j移动一定步长,那么在t+1时刻的移动公式如式(3)。
式(3)中,s为移动步长。
5) 邻域范围更新阶段
每个萤火虫采用自适应动态决策半径,在每次迭代的时候,根据邻居萤火虫的密度改变它的决策半径,当邻居密度越小,它就加大决策半径以寻找更多的邻居;反之邻居密度越大,就减小决策半径,调整公式如下:
式(4)中,β表示邻域变化率,nt表示邻居阈值控制萤火虫的邻居数目,rs表示萤火虫感知范围,rdi(t)表示t时刻第i只萤火虫的动态决策范围且0 ≤rdi(t) ≤rs。
萤火虫的算法流程图如图1所示。
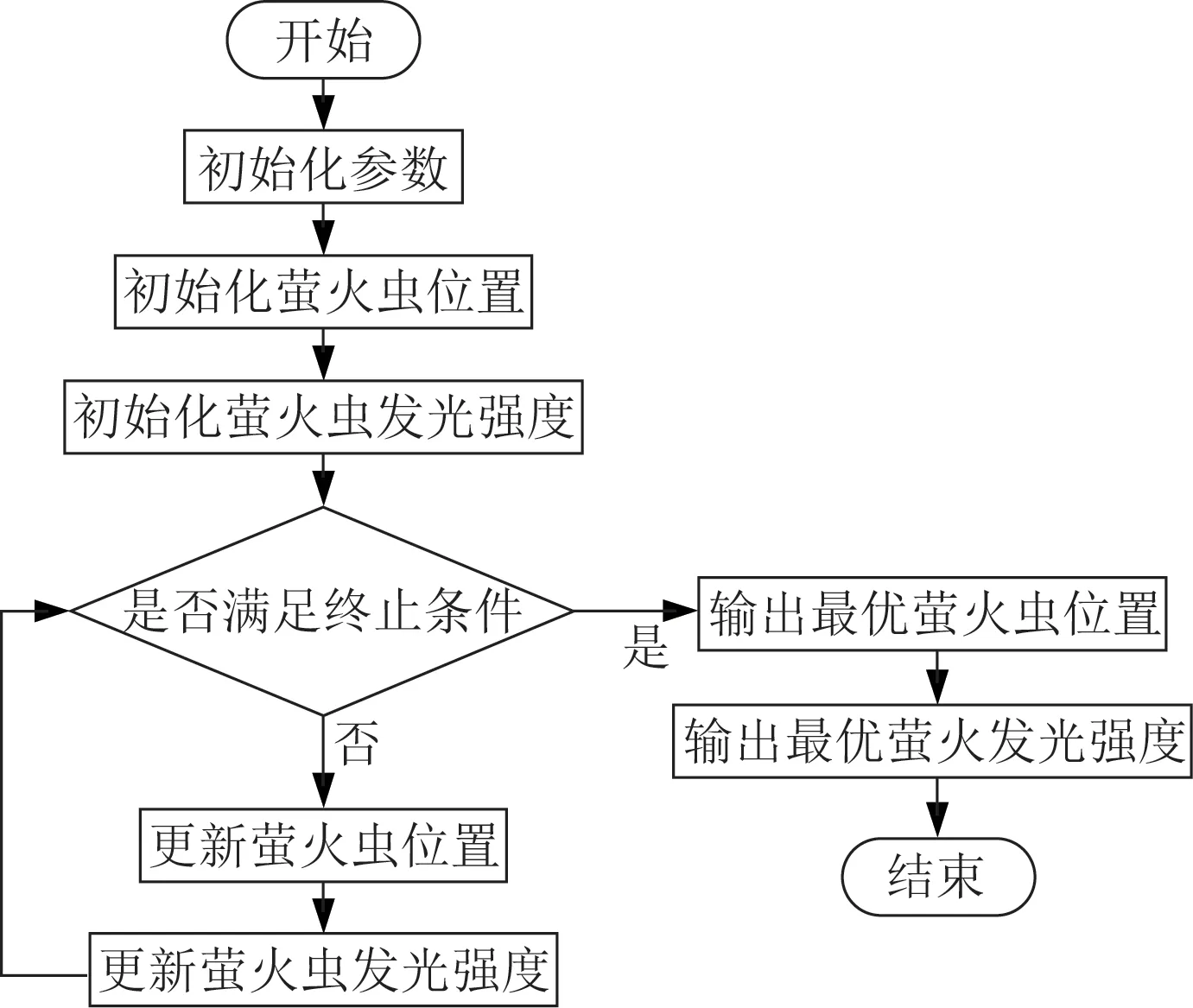
图1 萤火虫算法流程图Fig.1 Firefly algorithm flowchart
1.2.2 BP神经网络
反向传播(Back Propagation,BP)算法是多层感知器的一种有效学习算法,它把一组负荷样本的输入输出问题变成一个非线性优化问题,使用最优化中最常见的梯度下降算法,用迭代运算求解权值以及解决相应的学习记忆问题,同时加入了隐含层节点,使得优化问题的可调整参数增加,从而使得预测模型得到精确解[22]。
BP算法的基本步骤如下:
1) 初始化权值w和阈值b,即把所有权值和阈值都设置成较小的随机数;
2) 提供训练样本集,包括输入向量P和要求的预期输出T;
3) 计算隐含层和输出层的输出。对于图2而言从隐藏层到输出层可得式(5)。
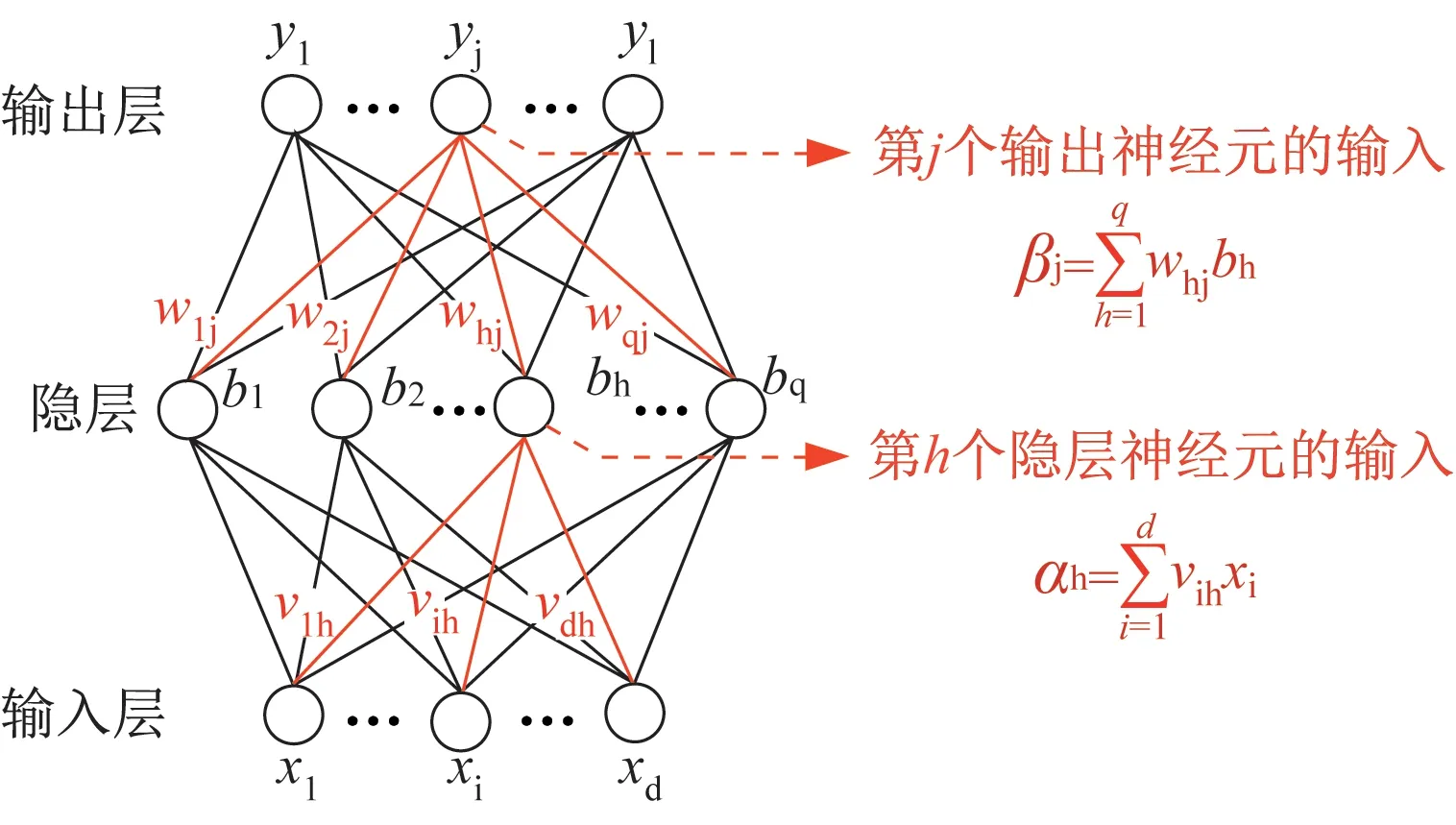
图2 三层BP神经网络结构图Fig.2 Three-layer BP neural network structure diagram
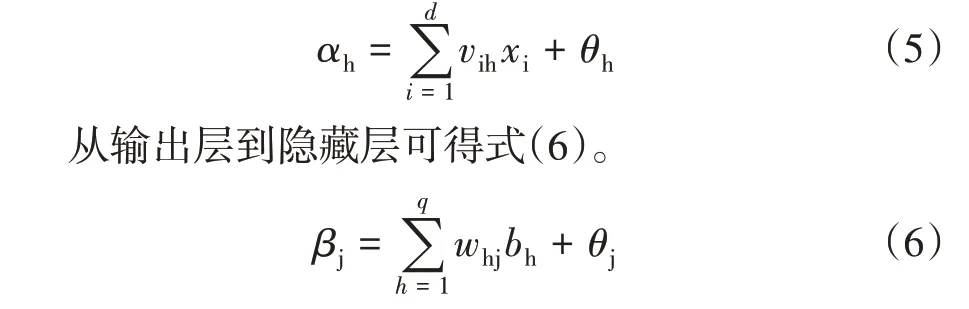
4) 调整权值和阈值,标准的BP 神经网络的权向量调整公式为
式(7)中,w(k+ 1)、w(k)分别为k+1、k时刻的权向量,η是学习率,D(k)是k时刻的负梯度。按误差反向传播方向,从开始输出节点开始返回到隐含层按式(7)修正权值。阈值也是一个变化值,在修正权值的同时也在修正阈值,原理同权值修正。
5) 计算网络误差均方和E
6) 循环步骤2 至步骤5,直至误差均方和满足精度ε为止,即E<ε。
1.3 FA-BP神经网络相对比传统BP神经网络的改进
通过之前对于BP神经网络的大量研究,发现其仍旧存在很多局限性和缺点,比如学习过程的收敛速度慢、学习率不稳定、误差平方和函数可能有局部极小点出现等情况;而萤火虫优化算法是一种基于群体智能的优化算法,能较快地找到全局最优值,并且参数对于算法的影响较小。在本文中利用萤火虫算法结合BP神经网络,可以获得更好的网络初始连接权值和阈值,而该优化算法在预测问题中有较高的精度和较好的拟合能力,避免了BP神经网络对初始值的敏感和训练过程中可能有局部极小点出现的问题,提高了BP神经网络的泛化能力、收敛速度和学习能力。
2 实例分析
2.1 预测模型评价指标
选取山东省某市2019年-2022年每年1月的电力负荷数据作为电力负荷预测的历史负荷数据,利用历史负荷数据来预测该市的电力负荷预测。采用MATLAB 仿真软件对数据进行训练和仿真,设置网络进化参数,其中训练次数设置为100次,学习率设置为0.01,训练目标误差为0.000 01。利用训练好的FA-BP神经网络模型进行预测,选取BP神经网络模型作为对比模型。
本文选用平均绝对误差(MAE)、均方误差(MSE)与均方根误差(RMSE)综合评价各模型的预测精度,计算公式如式(9)-式(11)。

2.2 结果分析
为了验证本文所用方法的准确性,使用MATLAB编程语言进行仿真,选择标准BP神经网络预测模型作为比较组。选取历史负荷数据、历史最高与最低温度、平均湿度以及当年的GDP作为网络的输入,即确定输入节点个数为5,网络输出为电力负荷预测值,即输出节点个数确定为1,然后对网络进行训练,当隐藏层节点数为4时,网络性能最佳,最后经过仿真测试之后得到的预测结果如图3所示,FA-BP 神经网络模型与BP神经网络模型的误差对比如图4所示。可以看出FABP 模型的预测误差小于BP 模型,而其预测值也比BP神经网络更接近真实值。
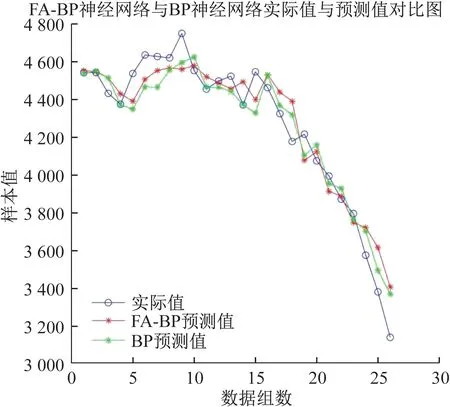
图3 预测结果对比图Fig.3 Comparison chart of prediction results

图4 预测误差对比图Fig.4 Comparison chart of prediction errors
从表1 中可以看出,本文所构造的FA-BP 模型比传统BP 模型的MAE、MSE以及RMSE都更小,具体表现为MAE下降了10.487 3,MSE下降了6 945.171 6,RMSE下降了29.428 2,证明本文所构建的模型预测结果更加准确,由此说明相比起传统的BP 神经网络,FA-BP 神经网络的网络性能更好,对于电力负荷预测也能得到更加精确的模型。
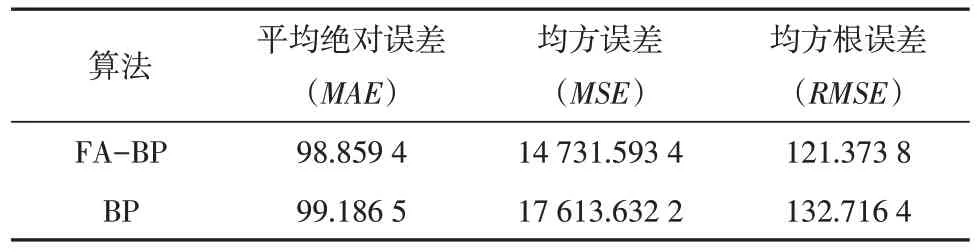
表1 FA-BP神经网络与BP神经网络误差对比表Table 1 Error comparison table of FA-BP neural network and BP neural network
3 结语
本文针对传统BP 神经网络预测模型算法进行改进,通过引入萤火虫算法优化了BP神经网络的预测准确性,同时使用主成分分析进行数据的预处理,将各种变量的影响纳入考量范畴。通过FA-BP 神经网络预测模型与BP 神经网络预测模型进行对比,可以发现FA-BP 神经网络算法的MAE、MSE和RMSE均小于BP神经网络的对应值,可得出FA-BP神经网络预测方式具有更高精确度的结论。
本文提出的电力系统短期负荷预测的优势在于:
1) 使用主成分分析进行数据预处理,能够将诸多对电力系统负荷造成影响的因素纳入考虑范畴,大大增加数据预测实用性。
2) 使用萤火虫算法对BP 神经网络进行优化,在提高算法预测精准度的前提下,具有操作方便、使用简单等优势,具有工程实践意义。

