基于器件参数的五冗余捷联惯组配置方法

林业丰,谢 波,姚安逸,祁 帅,黄茂源

(西安航天精密机电研究所,陕西 西安 710100)

0 引言

随惯性导航系统开始趋于民用化,市场对惯导系统成本、体积与可靠性的要求也不断提高,采用冗余技术,通过增加一定数量惯性仪表并开发配套处理器,使其成为拥有较高可靠性的惯性导航系统[1]。

当下对冗余系统的研究主要可分为四冗余(八表冗余)、五冗余(十表冗余)、六冗余(十二表冗余)等。四冗余系统体积小、成本低、有固定的安装角度,可以适应更多的安装环境,但系统自由度仅为1,故其在各轴安装同样器件的情况下导航可靠性与导航精度均低于其他冗余系统;六冗余系统采用正十二面体构型,理论上是使系统可靠性与导航精度均能达到最优的结构配置,但在各轴均安装同样器件的情况下,该系统面临体积大、成本高等问题,对其安装环境有极大限制;五冗余系统相对四冗余系统多出一个余度,有更高的可靠性,相对六冗余系统体积更小,经济性更高,能适应更多种导航需求。我国的“长征四号丙”运载火箭、“长征六号”遥八运载火箭、“长征二号丙”运载火箭等就搭载了五冗余光纤惯组进行导航。当下对五冗余系统多为研究当五轴均配置同型号仪表时导航系统精度提升情况。文献[2]提出了通过最小二乘法进行五冗余捷联惯组的最优配置确定方法;文献[3—4]提出了一种技术指标,以保证冗余惯组数据融合精度,并对冗余惯组故障检测精度进行了分析;文献[5]提出了通过穷举法进行五冗余捷联惯组最优安装角的确定方法;文献[6]等提出了一种惯组信息一致性检验与信息融合的方法;文献[7—8]提出了直接以仪表零漂作为加权系数的加权矩阵构造方法;文献[9]提出了考虑仪表杆臂误差下的最优配置方法。但现有的研究中均未从仪表参数入手考虑惯组构型与构型后数据融合方法,当惯组成本和体积受限制时,斜置轴通常选择安装精度略低但体积更小的器件,若不考虑仪表参数直接进行器件构型与数据融合,导航精度很有可能不如仅使用正交三轴器件进行导航[10]。通过仪表参数计算器件最优安装角度、选择最佳数据融合的方法后,可以抑制测量数据中的随机误差,进一步提升导航精度。

本文针对各轴测量仪器精度不相同的五冗余捷联惯组,通过加权最小二乘法对加权矩阵的选择、各轴仪器最优安装角度及各种配置方法对仪器精度的要求进行了理论性的分析,提出一种适用于各种仪表配置方案的捷联惯组配置方法。

1 捷联惯组安装结构

对于冗余捷联系统而言,斜置冗余仪表用于故障检测和隔离,同时还可通过数据融合技术,将斜置轴器件测量数据利用起来,保证系统可靠性的同时,提高惯导系统的测量和导航精度。通过多传感器数据融合技术,充分利用所有的冗余测量数据,可以有效抑制测量数据中的随机误差,为提高惯导系统导航精度提供了另外一条有效途径。通过冗余仪表参数选择合适的安装角度与加权矩阵,可以使数据融合时加权最小二乘估计的均方误差阵达到最小,从而使惯组导航精度得到进一步提升。

捷联惯组具体安装方案如图1,其中g1、g2、g3、g4、g5为陀螺仪和加速度计(各方向均配置一个陀螺仪和一个加速度计),共十表,故五冗余捷联惯组又称为十表冗余捷联惯组,g1、g2、g3分别沿X、Y、Z三正交轴轴向放置,g4、g5沿任意方向两个斜向轴放置。L、K分别为g4、g5在XOZ平面的投影线;α1、α2分别为g4、g5所在斜置轴绕OZ轴正向逆时针旋转至OY轴正向的角度;β1、β2为别为g4、g5所在斜置轴绕OY轴正向顺时针旋转至OZ轴正向的角度。

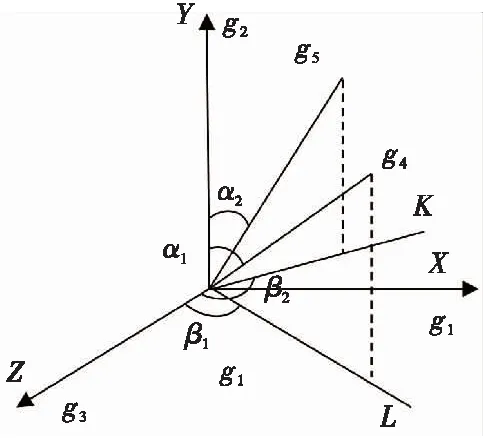
图1 三正交两斜置结构配置示意图

不考虑器件的安装误差,此时安装矩阵为

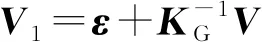
2 五冗余捷联惯组轴向配置方法

在考虑成本和体积的情况下,可选择精度较低但体积较小的器件作为斜置轴器件,斜置轴器件测量精度的下降必然会带来相对各轴均配置相同器件时导航精度的损失,但这种损失可以通过选择合理的安装角度与加权矩阵的方式,通过数据融合的方法来减小。当使用冗余系统进行量测时,若想将各表量测数据均加以利用,由于安装矩阵非方阵,一般采取最小二乘法对数据进行拟合,但当各轴向仪表精度不同时,为了更好的融合效果,应选用加权最小二乘法根据各表精度调整权重,并通过加权矩阵,计算出该组器件最适合的安装角度。

2.1 加权矩阵选取

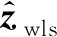
由于噪声方差阵CV为正定阵,即它总可以平方分解为CV=STS且S可逆。记A=HTS-1,B=SWH·(HTWH)-1,显然有AB=I,根据许瓦茨不等式:

[B-AT(AAT)-1AB]T[B-AT(AAT)-1AB]=
BTB-(AB)T(AAT)-1AB≥0,
BTB≥(AB)T(AAT)-1AB=(AAT)-1

即

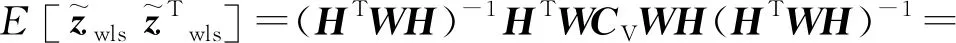
(1)

不难验证,式(1)成立条件为W=aCV-1(a为任意常数),此时加权最小二乘估计的均方误差阵最小,即此时导航精度最高。

2.2 安装角度推算

设立指标F=|G|, 由于H的每行分别是5个测量轴的方向余弦。则有

(2)

该方程组为一矛盾方程组,现将其线性化为

a21=O2×6,a12=O3×4。

可得方程aX=b,由于该方程组不相容,故取其唯一极小范数二乘解为

此时得到以下方程组:

(3)

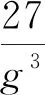
2.3 冗余器件配置要求

对低成本五冗余系统而言,冗余器件安装方案可分为两种:两个斜置轴配置不同精度的低精度器件,正交轴配置同精度高精度器件,此为方案一;两个斜置轴配置同精度低精度器件,正交轴配置同精度高精度器件,此为方案二,方案二可视为方案一的特殊情况。下面对两种配置方案冗余器件配置要求进行推导,由于导航时器件主要噪声来自于器件零漂且器件零漂易于获得,故推导时器件噪声均用零漂代替。

方案一:设冗余器件1标度因子为k1,器件零漂为θ1,冗余器件2标度因子为k2,器件零漂为θ2,正交器件标度因子为k0,器件零漂为θ0,且k1=ak0,θ1=bθ0,k2=ck0,θ2=dθ0;其中a、b、c、d均为正实数且均大于1。此时冗余轴1安装角度余弦值为

(4)

(5)

(6)

(7)

方案二:设冗余器件标度因子为k1,器件零漂为θ1,正交器件标度因子为k0,器件零漂为θ0,且k1=ak0,θ1=bθ0,其中a、b均为正实数且均大于1。此时冗余轴安装角度余弦值为

(8)

(9)

cos2α1=1/3,

(10)

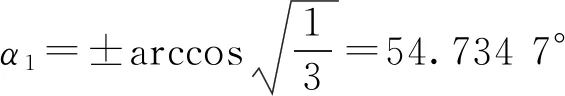
(11)

可见,当斜置的两轴均配备同精度的器件时,其器件精度不会对配置造成限制,且该种配置下的惯组不用额外计算安装矩阵,直接按上述角度安装即可。

3 仿真验证

由于在导航过程中,仪表零漂对导航精度起主要影响,本次仿真在仅考虑器件零漂情况下对载体进行20 min静态仿真模拟,以验证该配置对载体飞行精度提升效果。

α1=54.734 7°或125.264 4°,

α2=54.734 7°或125.264 4°,

β1=±45°或±135°,

β2=±45°或±135°。

选择α1=54.734 7°,α2=125.264 4°,β1=-135°,β2=-135°,此时|G|=0.842 3,该配置下|G|最接近0.839 6,安装结构如图2所示。

图2 仿真方案结构配置示意图

设置初始误差为0,静态仿真20 min,其中前5 min进行对准,后15 min进行静态导航仿真,进行100次仿真,每次仿真随机生成误差。选择指标为CEP指标,即包含50%飘移点的圆的半径。仿真结果如表1所示。

表1 CEP指标(含50%漂移点圆的半径)对比

静态导航仿真误差变化如图3所示。

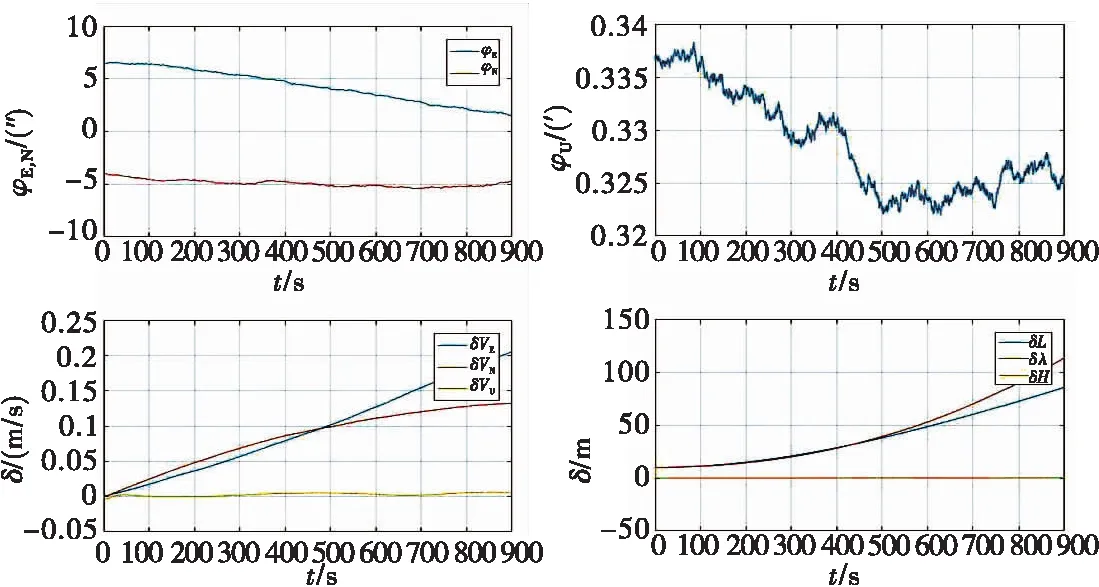
图3 静态仿真导航误差

分析上述数据,可以发现:采用配置0时,五轴导航相比三轴导航位置误差减小10.89%,加入合适的加权矩阵后,相比未加入加权矩阵导航位置误差减小9.5%,相比三轴导航位置误差减小19.35%;采用配置1,即未通过仪表参数确定安装角度时,数据融合后相对三轴导航,位置误差反而提升了21%。这可能是由于冗余轴仪表精度相对正交轴仪表精度相差较远,相比原文使用斜置轴仪表零漂为正交轴仪表零漂的1.5倍,本文斜置轴仪表零漂约为正交轴仪表零漂的3.33倍,此处也说明根据仪表参数配置惯组安装角度的工程实用性。

4 结论

本文提出一种在成本体积预算有限的情况下,五冗余惯组基于仪表精度参数确定加权矩阵和仪表安装角度的方法。该方法通过计算加权二乘估计的均方误差阵,得到基于该配置下的最优加权矩阵及最小均方误差阵,再由最小均方误差阵计算最优配置角度,并对五冗余惯组配置要求进行了推算。仿真证明,经该方法得出的配置方案,相比三轴导航位置误差减小10.89%,加入合适的加权矩阵后,相比未加入加权矩阵导航位置误差减小9.5%,相比三轴导航位置误差减小19.35%。

本文针对冗余惯组各轴配置不同精度测量仪器的情况,通过加权最小二乘法对加权矩阵的选择、各轴仪器最优安装角度及各种配置方法对仪器精度的要求进行了理论性的分析。在后续工作中将对本文提出的配置方法进行实验验证。