基于数据挖掘的短期电力负荷预测方法

潘 攀，陈 凡

（国网浙江省电力有限公司温州供电公司，浙江 温州）

引言

电能生产具有一定特殊性，电力系统内部无法大量储存电力负荷，所以在电力系统供电过程中需要精准掌握用户负荷的变化动态平衡，实现用户用多少负荷电网就生产多少负荷，这一过程就是电力系统的短期电力负荷预测。文献[1]提出Dropout-ILATM预测模型，解决了传统方法难以处理负荷数据间关联的问题，适用于更多预测宽度的负荷预测；文献[2]设计Prophet 和XGBoost 相混合的预测模型，可以准确快速地预测电力负荷。但电力负荷的产生是一个随机非平稳过程，历史负荷观测值具有波动性，导致传统方法的精度不够，因此，提出关于短期电力负荷预测方法的研究。

1 挖掘相似日电力负荷数据

本文参考模糊聚类原理挖掘历史电力负荷数据的规律，从而选取相似日[3]，简单来说就是根据模糊规则构建电力负荷特性指标数据的模糊系数特征映射表，并挖掘负荷数据之间的规律，该方法可以有效降低负荷随机性，进而提升挖掘精度。假设两个不同的电力负荷数据样本分别为那么为构建样本数据的模糊相似矩阵[4]，需要根据下式求出这两个样本之间的相似程度：

式中，smn表示电力负荷数据Xm与Xn之间的相似度。在式（1）的基础上，即可构建电力负荷数据样本空间的模糊相似矩阵[5]，表达式如下所示：

式中，S 表示电力数据的模糊相似矩阵。根据式（2）所求模糊相似矩阵，即可完成相似日的选取，通常一个相似矩阵就可以获得一个样本数据的分类，在根据传递闭包设置一个合适的阈值后，就可以利用该阈值对矩阵进行截割，以此实现电力负荷数据的动态聚类，最终分类结果即为相似日选取结果。在选取相似日的过程中，为筛选出最为接近的相似日，可以对预测日与历史日之间的相似程度进行排序，以此确定最佳的相似日，保障挖掘相似日电力负荷数据的有效性。在相似日确定后，最后对选取的相似日电力负荷数据进行提取，以此作为后续负荷预测样本。

2 预处理电力负荷数据

历史相似日电力负荷数据是本文所设计预测方法的基石[6]，挖掘的相似日数据质量将直接影响本文设计方法的预测精度，所以为保障后续负荷预测的正确性与有效性，本文在上述研究内容的基础上，对挖掘数据进行一定的预处理[7]。一般来说，受电力系统自身以及外界环境等因素的影响，会导致挖掘的相似日电力负荷数据存在异常值，所以本文首先对相似日数据做清洗处理，数据清洗主要分别两步，一是电力负荷数据异常值的辨识，这里本文采用绝对中位差法进行异常数据的辨识，对于相似日的电力负荷数据来说，异常数据辨识的具体流程如下：获取电力负荷数据集合的平均值X；根据该平均值与集合中各采样点数据之间的绝对偏差，即可求出绝对偏差的中位数W，计算公式如下所示：

式中，median 表示中值函数。根据上式确定中位数后，即可掌握相似日电力负荷数据的合理取值范围并将超出该范围的负荷数据判断为异常数据，本文以X'表示相似日的异常负荷数据。二是对辨识出的异常数据X'缺失值进行补全操作，这里本文采用拉格朗日差值法进行缺失数据的补全，就是通过负荷数据点之间连续性的变化规律，以缺失点前后的数值对缺失点进行插值修复，表达式如下所示：

式中，I（X'）表示异常电力负荷数据缺失点插入的缺失值近似值；a1…an表示多项式。与此同时，为避免不同量纲差别为负荷预测带来的误差，本文还需要对挖掘相似日数据进行归一化处理[8]，也就是将挖掘数据按一定比例全部缩放至一个特定的区间中，使其量纲一致，本文主要采用下式所示的最小- 最大归一化处理原始数据：

式中，X0表示归一化后的相似日电力负荷数据，其取值区间为[0,1]；X 表示原始相似日电力负荷数据；Xmin、Xmax分别表示相似日电力负荷数据集中的最小与最大数据。利用式（5）处理数据，可以实现相似日电力负荷数据的等比例缩放。综上，本章对挖掘的相似日电力负荷数据做了两个主要预处理工作，分别是数据清洗与数据归一化，通过数据清洗可以将原始负荷数据中的异常值修复，通过数据归一化可以将不同量纲的原始数据转换映射至相同特定区间中，将经过预处理后的相似日电力负荷数据用于后续预测环节，可以保障数据质量。

3 短期电力负荷预测

前文通过对电力系统历史相似日的各类电力负荷数据进行深入挖掘并预处理后，形成了训练样本数据，本章将基于上述数据构建SVM模型，从而形成短期负荷的预测[9]。支持向量机（SVM）属于统计学习范畴，主要是针对分类问题研究出来的，将其应用于电力系统短期负荷预测中，在预测过程中不会陷入局部最优[10]，而且具有较好的推广性。本文所构建的SVM预测模型，与常规神经网络有着相似的网络结构，均由输入、隐藏以及输出层组成，但不同的是，本文建立的SVM模型隐藏层的神经元节点个数利用电力负荷数据样本中支持向量数目来确定，这样可以避免模型在训练过程中陷入局部极值[11]。那么SVM预测模型的具体建模过程如下：一般来说，线性回归问题的本质就是通过一个合理的函数，求解出样本数据的对应输出值，本文所构建的SVM预测模型也是这样，当相似日电力负荷数据输入模型时，通过线性拟合函数将输入数据映射至高维空间中，从而得到输出值，该函数的表达式如下所示：

式中，Y 表示模型输入变量对应的输出值；T 表示模型输入变量原始特征空间的维数；α（X）表示模型输入相似日电力负荷数据的线性映射函数；表示Y 与α（X）之间的点积运算；p 表示阈值。在式（6）基础上，参考结构风险最小化原则，即可确定SVM 预测模型的最优回归函数，表达式如下：

4 仿真实验

4.1 实验准备

本章选择我国某地区2022 年12 月的电力系统的电力负荷数据作为实验数据，展开仿真实验，以对文中设计的短期电力负荷预测方法的优势进行验证。在本次仿真实验中，以本文设计基于数据挖掘的预测方法作为实验组，并选用基于BP 神经网络的预测方法、基于LSTM网络的预测方法作为对照组。首先，将收集的实验数据中前20 天的电力负荷数据作为训练样本，后10 天的电力负荷数据作为测试样本，其中测试样本的原始电力负荷数据曲线如图1 所示。

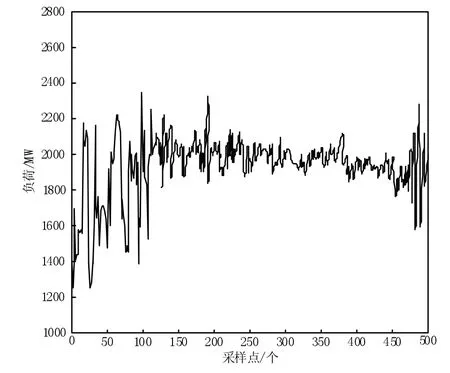
图1 原始电力负荷曲线

在此基础上，先采用训练样本分别对实验组方法与对照组方法进行训练，实现各方法下预测模型最优参数的设置；再采用图1 所示测试样本分别输入三种不同的预测模型中，从而获得最终电力负荷预测结果。

4.2 实验结果

经过不同预测模型的训练与测试后，所得最终电力负荷预测对比结果如图2 所示。

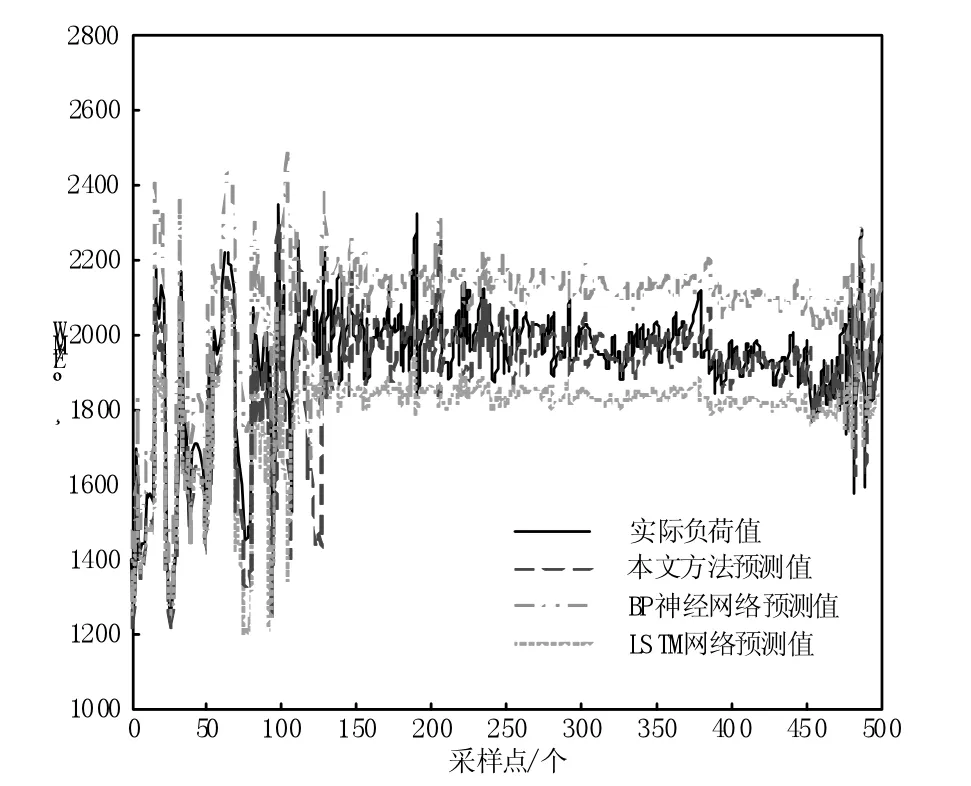
图2 电力负荷预测结果

通过图2 可以发现，整体来说，本文设计方法预测的短期电力负荷曲线，与原始负荷曲线之间的拟合效果较对照组方法更好，说明本文设计方法下的短期电力负荷更接近于真实值。为进一步对比实验组方法与对照组方法的预测性能，本文以下式所求误差作为预测方法的评价指标：

式中，ε 表示平均绝对叟分比误差；N 表示电力负荷采样点数量；H（i）表示第i 个采样点的电力负荷实际值；H'（i）第i 个采样点的电力负荷预测值。根据上述内容，分别求出每种方法下的绝对叟分比预测误差，结果如表1 所示。

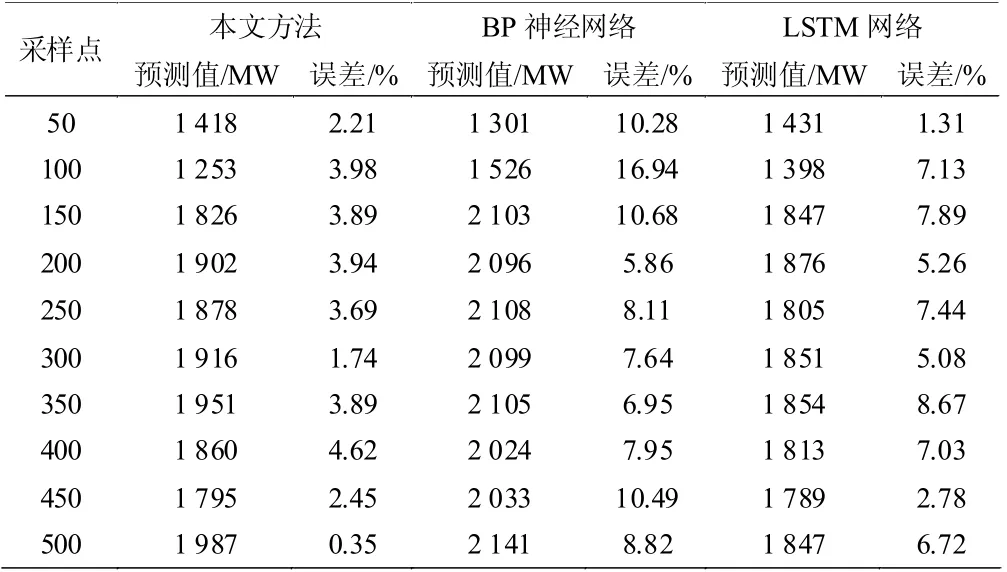
表1 不同预测方法的性能对比

从表1 中数据可知，基于BP 神经网络的预测方法的平均绝对叟分比误差为9.37%，基于LSTM网络的预测方法的平均绝对叟分比误差为5.93%，而本文设计方法的平均绝对叟分比误差为3.08%，较对照组方法降低了6.29%、2.85%。由此可以说明，本文所提基于数据挖掘的短期电力负荷预测方法是有效且可靠的，整体预测精度较高，满足电力系统的用电负荷预测需求。

结束语

在我国国家与民众对电力需求不断增加的大背景下，电力负荷预测不仅影响电力系统的供需平衡，而且影响系统供电可靠性，所以如何精准有效地预测电力系统短期电力负荷已经成为我国社会热点问题。基于此，本文设计一种基于数据挖掘的预测方法，文中通过挖掘相似日的历史用电负荷数据，完成了负荷预测，并通过仿真实验验证了设计方法的优越性。当然，目前本文仅针对电力系统的短期负荷做了预测，设计方法是否可以同时精准预测长期电力负荷有待进一步深入研究。