FD-MIMO 下行系统中基于空时码下的联合选码方法*

孔婉冰，戴谭明，吴君钦

（江西理工大学，江西 赣州 341000）

0 引言

大规模多输入多输出（Multiple Input Multiple Output，MIMO）技术可提升系统的频谱效率和传输可靠性而备受学术界和工业界广泛关注[1-2]。在该系统中，基站配置多达数十根甚至上百根天线，大量的天线能充分挖掘并利用空间维度资源，在同一时频资源下服务于多个用户。

实际应用场景中，在有限空间部署大量线性阵列天线挑战性极大，为了实现这一目标，提出了三维多输入多输出（Full Dimension Multiple Input Multiple Output，FD-MIMO）技 术。在FD-MIMO系统中[3-5]，为了高效利用空间自由度且合理地部署大量天线并同时发挥其优势，天线往往以二维或者三维阵列形式排布，也就是说，水平和垂直方向都安置天线。在该系统中，信道状态信息（Channel State Information，CSI）的获取尤为关键。在时分双工（Time Division Duplexing，TDD）模式下，因信道具有互易性[6-7]，基站能够利用上行的CSI 估计下行的CSI。而在频分双工（Frequency Division Duplexing，FDD）模式中，上下行链路通过不同频率加以区别导致信道不具备互易性，此时，下行链路CSI 需要通过反馈来获取。本文是基于FDD 下的FD-MIMO 有限反馈系统中的空时码下的联合选码策略的研究。

在FD-MIMO 下行系统中，预编码技术不仅能有效地增强期望信号，而且能抑制用户之间的信道干扰，但是无法抵抗信道的深度衰落。而空时编码技术虽能够抵抗深度衰落，却无法有效地抑制干扰。于是，尝试将两种技术结合，在得到分集增益的同时复用增益也得到加强，且在不增加带宽的情况下，能大幅度提升系统容量和频谱利用率[8-9]。目前在这方面的研究主要有：文献[10]提出了基于离散傅里叶码本的双重码本设计策略，该策略基于二维信道具有较好的性能。文献[11]使用格拉斯曼（Grassmanian）码本分别量化水平和垂直方向上的信道信息，再通过张量积运算获得最终的预编码码字[7]。文献[12]对重构信道矩阵进行奇异值分解，并分别用离散傅里叶码本对最大奇异值对应的一组特征向量进行量化，最后通过张量积运算得到最终码字。虽然最大奇异值对应的特征向量能反映出部分信道特性，但存在一定的局限性。于是，本文结合空时编码技术和联合选码策略提出了新的发送方式，即在相干时间内通过多次发送，使得同一信号通过不同的信道传送至接收端。为了在发送方式上提供完全增益的空时码，采用Alamouti 正交空时码[13-15]。而在接收方利用最大似然（Maximum Likelihood，ML）解码方式，因为发送信号满足正交性，所以在解码时可转化成线性解码以降低解码复杂度。

1 系统模型

本文采用文献[5]中的信道假设模型，天线的排布结构为均匀平面阵列（Uniform Planar Arrays，UPA），在水平和垂直两个维度上均有波束成形增益，基站端安装有N根天线，其中Nv表示垂直方向上的天线数，Nh表示水平方向上的天线数。dv表示垂直方向上的天线间距，dh表示水平方向上的天线间距。

假定基站与天线之间存在P个辐射路径，其中每个辐射路径表示为[16]：

2 传输方案及解码策略

2.1 基于Alamouti 码的传输方案

在引入Alamouti 码传输方案之前，需要引入预编码码本。在目前的理论研究和实践中，离散傅里叶码本在FD-MIMO 系统中受到广泛关注。该码本的形式如下：

式中：Bv为垂直方向反馈比特数；Bh为水平方向反馈比特数。

对于选码的过程，文献[12]中已给出一种方案，具体过程如下文所述。首先有：

式中：为信道h中的第1 个元素到第Nv个元素构成的向量。也就是将信道h重构成Nv×Nh的信道矩阵H，再对其进行奇异值分解，则有：

式中：A和B分别为左、右奇异值矩阵；Σ为对应奇异值组成的对角阵。

对a1和b1向量进行量化，其中a1和b1分别是信道矩阵H经奇异值分解后矩阵A的第1 列和矩阵B的第1 列，采用如下量化准则：

然而，上述方案只考虑了一对奇异值向量，并不能还原真实信道。于是，提出了基于多对奇异值联合量化的策略。而量化的奇异值向量越多，反馈开销也会随之增大，因此选择两对奇异值向量量化较为合理。用两组向量逼近真实信道可写成：

式中：δ1，δ2为重构信道矩阵经奇异值分解得到的前2 个特征值。使用这两对奇异值向量进行联合量化的形式如下：

有了选码方案后，为了便于研究，假设系统是单用户单天线。基站侧利用码本和Alamouti 码给用户端传送数据。传送的步骤为，先将要传送的数据s1和s2映射到Alamouti 码中，且数据均属于星座QAM。Alamouti 码的具体形式如下：

式中：为复数的共轭复数。

2.2 极大似然等价线性解码策略

极大似然解码的基本思想是将接收到的信号与所有可能的传输信号进行逐一比较，然后根据最大似然估计准则估计该信号。显然，解码复杂度随信号的增加而呈指数级增长。因此，如何将非线性译码转化为线性译码尤为重要。

从发送接收方程可得用户第1 次、第2 次发送接收方程为：

3 反馈开销及复杂度分析

根据辐射路径与码本的结构，给出了反馈比特数下限的表达式：

式中：表示对x向上取整；角度识别率Ω越小，基站天线数越多，则需要的反馈开销的下限就越大。开销越大，码字数量就越多，量化就越均匀，此时码字与真实信道的偏差就越小，那么信道的增益就越大。综合考虑反馈开销和增益，Ω合适的取值为π/4 或者π/8。

下面对式（18）进行解释：

为使得全部天线都能产生增益，需要所有角度都集中在某一特定的区间。假定反馈比特数为Ba，则码本的码字数为2Ba，于是每个角度区间长是2π/2Ba。由于选码时最糟糕的情况是刚好落在区间正中央，在这种情况下，信道与码字角度的差值是区间长的一半，则有：

针对本文所提方法的复杂度分析如下：由于假设基站侧垂直方向上的天线数为Nv，水平方向上的天线数为Nh，因此生成离散傅里叶（Discrete Fourie Transform，DFT）码本的复杂度为信道矩阵奇异值分解（Singular Value Decomposition，SVD）的复杂度为用两组特征值进行量化的复杂度为o(2Bv+Bh(NvNh+1)NvNh)。相较于单独选码方案，本文所提方案虽然复杂度稍大，但更能逼近真实信道。因此，本文所提方案的总复杂度为：

4 仿真结果

为了证实所提方法的性能，本节从3 个方面进行仿真验证。仿真1 验证了联合量化选码相较于单独选码的优越性；仿真2 是基于不同的量化方案，在合适的反馈比特数下，将本文方案与单独选码方案在误码率方面进行比较分析；仿真3 证实了在不同天线配置的情况下，合理的反馈比特数。表1 给出了相关参数。

表1 系统仿真参数设定

4.1 仿真1

图1 给出了联合量化选码方案与单独选码方案的误码率对比，反馈比特数Bv=Bh=4，其他相关仿真参数按照表1 进行设置，天线阵列数为N=Nv×Nh=4×4，反馈比特总数为8 bit。从图1 中可以看出，随着信噪比的增大，误码率在不断下降，联合量化选码方案相较于单独选码方案下降的幅度会更大些，尤其在较高信噪比的情况下，大概高出2 dB。虽然联合量化复杂度高于单独量化，但复杂度也在可接受的范围内。

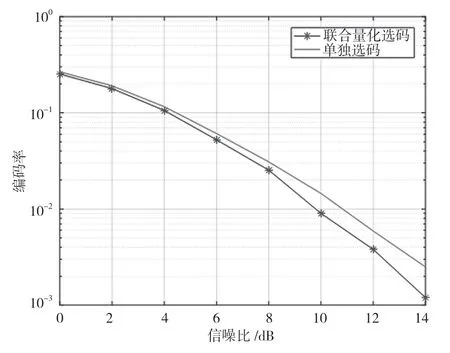
图1 不同选码方式下的误码率

4.2 仿真2

图2 给出了联合量化选码方案与单独选码方案的误码率对比，反馈比特数分为两种情况：第1 种情况设置为Bv=Bh=3，总反馈比特数为6 bit；第2种情况设置为Bv=Bh=5，总反馈比特数为10 bit。其他相关仿真参数按照表1 进行设置，天线阵列数为N=Nv×Nh=6×6。从图2 中可以看出，在反馈比特数相同的条件下，联合量化选码的性能优于单独选码，在相同的选码准则下，反馈比特数越大，性能越好。由于反馈比特数越大，码字数量就越大，信道量化得更加均匀，更易逼近真实信道；但同时，反馈比特数越大，选码的复杂度就会越大，因此合理的反馈比特数显得尤为重要。

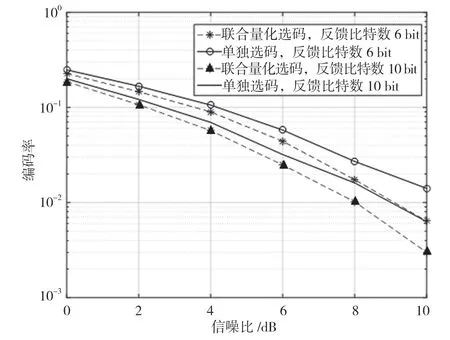
图2 不同选码方式下的误码率比较

4.3 仿真3

在图3 中，采用联合量化选码方案，仿真分成两组。第1 组设置基站天线配置N=Nv×Nh=4×4，信噪比越大，则误码率性能越好，但随着反馈比特数的增大，系统的误码率先下降得比较快，此后下降趋势趋于平缓。由图3 可知，图中横坐标表示一个维度上的反馈比特数，且两个维度上的反馈比特数相等。因此，当总反馈比特数为8 bit时，基本趋于不变。第2 组设置基站天线配置N=Nv×Nh=6×6，信噪比越大，则误码率性能越好，但随着反馈比特数的增大，系统的误码率先下降得比较快，此后下降趋势趋于平缓。由图3 可知，当总反馈比特数为10 bit 时，基本趋于不变。通过不同天线数的对比，也证实了反馈比特数的下限公式。

图3 不同天线配置下的误码率比较

5 结语

本文为了降低FDD 模式下的MIMO 下行系统的反馈开销，基于假设的信道模型给出了合适的反馈比特数的公式，其合理性在仿真中得到了证实。在此基础上，首先利用联合选码的预编码方案，可以更精确地逼近真实信道。虽然该方案的复杂度稍大，但也在可接受范围内。其次利用空时码与联合选码技术相结合来传送数据，在接收方采用等价极大似然解码方法，降低解码复杂度。最后，对所提出的方案进行了仿真，其结果与理论分析 一致。