轮毂开关磁阻电机电磁特性负效应及其抑制

罗晓亮 王策 张洋瑞

（重庆交通大学，重庆 400074）

1 前言

开关磁阻电机（Switched Reluctance Motor，SRM）具有结构简单、成本低、调速范围宽等特点，在家用电器、航天器械及电动汽车等领域广泛应用[1-2]。然而，转矩波动和径向电磁力是电机振动与噪声的主要来源，严重阻碍了开关磁阻电机的发展与应用[3-6]。

针对此问题，一些学者从控制策略角度展开研究。文献[7]提出一种电流波形推导方法，以降低磁饱和区域径向电磁力总和，实现径向电磁力数值变化最小。文献[8]建立了外转子齿顶开槽径向电磁力分析模型，通过调整齿顶辅助槽口尺寸减小径向电磁力。文献[9]、文献[10]基于直接瞬时转矩控制策略，提出转矩在线补偿与脉冲宽度调制相结合的控制策略，能够有效抑制转矩波动。文献[11]将模糊控制与直接转矩控制相结合，有效抑制了开关磁阻电机转矩脉动，转矩控制效果和精度均得到提升。

控制策略的改变提高了控制器的复杂性和电机成本。因此，通过优化本体结构设计提升电机性能的研究得到重视[12]。文献[13]对电机槽口进行结构优化设计，削弱幅值较大的径向电磁力，并通过对定子开辅助槽抑制电磁振动。文献[14]通过对双定子绕组设置不同绕组匝数，对分段转子部分施加悬浮力使其保持悬浮，使转子所受径向电磁力相互抵消。文献[15]提出一种具有优化磁通屏障的新型转子，通过改变转子几何形状降低转矩波动。文献[16]、文献[17]在定子和转子齿极两侧开不同类型凹槽，调节齿极槽宽与深度以改变表面磁通密度，并基于改进磁场分割法计算气隙比磁导，验证了齿极两侧开槽可有效抑制转矩脉动。

上述文献主要针对开关磁阻电机电磁力或转矩波动进行单一分析和优化，综合考虑气隙偏心对径向电磁力和转矩波动的研究较少。针对此问题，本文利用傅里叶级数推导开关磁阻电机电磁参数关于电流和转子位置角度的关系曲线，通过麦克斯韦应力张量法对定子凸极表面及相邻槽进行路径积分求和，获得气隙偏心条件下电磁力的空间变化特性，分别在静态和瞬态工况下分析气隙偏心对电机电磁特性的影响规律，并通过灵敏度分析确定结构参数贡献权重，制定合理优化方案，以期在不同气隙偏心量条件下有效抑制电磁特性负效应。

2 开关磁阻电机模型

本文以8/6 极外转子开关磁阻电机作为研究对象，如图1所示，其中，Fru、Frb为偏心时定子凸极两侧产生的径向电磁力。该电机主要由外转子、内定子和支撑轴组成，根据磁阻最小原理，磁通经定子凸极、气隙、转子凸极形成闭合磁路驱动电机运行。在轮毂电机受到道路激励时，轴承刚度的存在和非簧载质量的增加造成电机定、转子产生相对位移，形成不同方向的气隙偏心，定子凸极两端的力不再保持相等。

该外转子轮毂开关磁阻电机结构参数如表1所示。

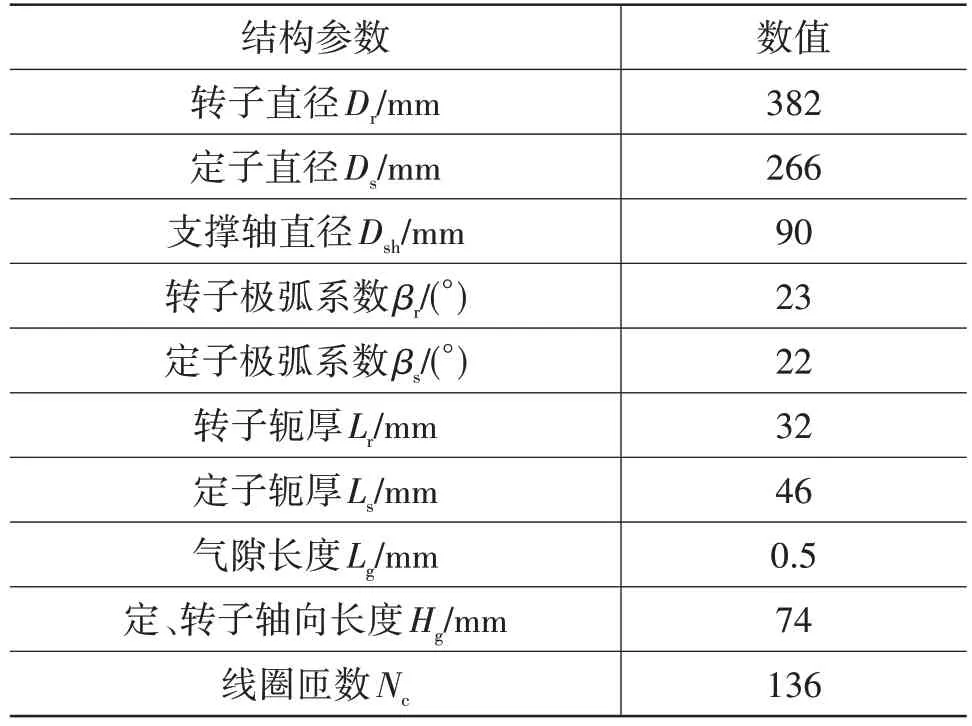
表1 SRM结构参数

2.1 机电耦合方程

假设定子凸极与转子凹槽中心重合位置处的转子位置角为转子位置初始角，该位置称为极对槽位置，当转子转动半个极距（τr/2=π/Nr，其中τr为转子极距，Nr为转子凸极数量）时，定、转子中心重合，此时为极对极位置，绕组相电感在二者位置之间呈线性上升、下降，因此，绕组相电感可以用傅里叶级数展开为：

式中，φn=nπ 为n次谐波分量的相位角；θ为转子位置角；i为绕组相电流，Ln为傅里叶级数的系数，由极对极、极对半槽、极对槽及其他特殊位置等关键绕组相电感导出[18]。

关键位置绕组相电感采用“极对极”绕组相电感Lu、“极对槽”绕组相电感La和“极对半槽”绕组相电感Lm[19]，则傅里叶级数的系数可写成：

其中，在“极对槽”位置时，定、转子之间气隙相对较大，假设绕组相电感Lu为常数[20]，则La和Lm可以表达为电流的多项式：

式中，an、bn为多项式拟合系数；N为in项数。

根据式（1），单相绕组相电感可写成：

基于上述分析，单相绕组相电感变化特性如图2 所示，拟合数据可以根据有限元仿真和试验结果获得，可以看出，电机的3个特殊位置拟合电感与有限元计算结果相比，拟合精度较好，证明其解析建模方法有效。

图2 绕组相电感拟合曲线

绕组相电感由磁链对绕组相电流偏微分获得，则磁链可以写成：

式中，cn=an-1/n、dn=bn-1/n分别为an、bn的拟合系数。

根据式（4）、式（5）可以得到不同转子位置角度和电流条件下的绕组相电感与绕组相磁链，拟合结果如图3所示，可以看出，随着转子从极对槽位置旋转至极对极位置，绕组相电感逐渐增大，电流在2 A时绕组相电感达到最大值126.58 mH，在极对极位置时绕组相磁链达到最大，并与电流变化趋势相同。电机的导通相应在电感的上升沿导通来建立所需驱动电流。

图3 SRM静态电磁特性

忽略绕组之间的互感，则绕组相的磁共能Wm可由位置相关联的绕组相磁链ψ(θ,i)对电流积分获得：

根据虚功原理和机电能量转化原理，可以得到开关磁阻电机定、转子凸极间的径向电磁力Fr、电磁转矩Te：

忽略定、转子凸极端部效应和互感，将式（5）代入式（7）可以得到绕组相的径向电磁力Fr：

开关磁阻电机是一种典型的磁阻电机，定、转子为双凸极结构，气隙偏心时定子凸极对称方向气隙出现不均匀现象，导致定子凸极对称方向的径向电磁力不再相同，产生不平衡径向电磁力，结合式（9）可以得到不平衡径向电磁力方程为：

式中，Lgb、Lgu分别为偏心时定子凸极和转子凸极之间的气隙长度。

根据式（7）、式（8）可以得到不同转子位置角度和电流条件下的静态力学特性关系，如图4所示，可以看出，绕组相电磁转矩与绕组相径向电磁力均随着电流的增大而增大，转子从极对槽位置旋转至极对半槽位置时，定、转子之间的气隙减小，电磁转矩与径向电磁力同时增大，在由极对半槽位置转向极对极位置时，定、转子重合度增大，电磁力切向分量逐渐减小，径向分量逐渐增大，在极对极位置时径向电磁力达到最大，转矩达到最小。

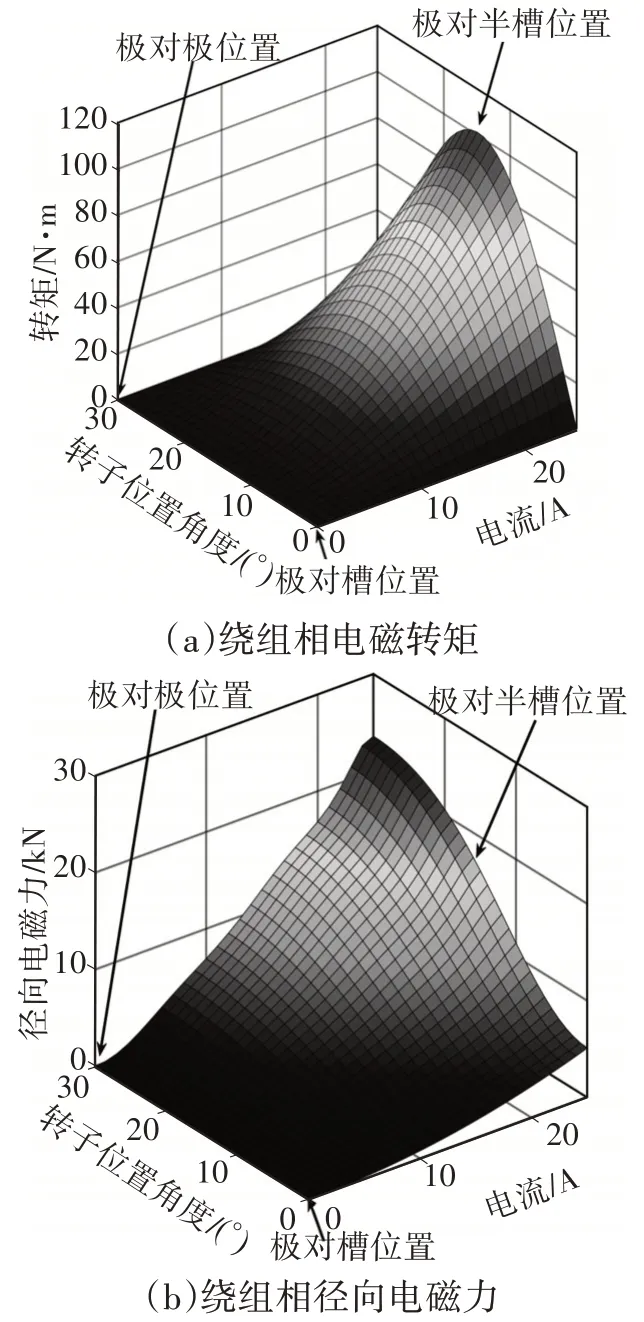
图4 SRM静态力学特性

2.2 电路驱动方程

基于上述分析，电流激励是影响开关磁阻电机电磁特性的因素之一，同时，电流激励由驱动电路参数控制。本文采用非对称半桥功率变换器控制，如图5所示，其中IGBT1~IGBT8为绝缘栅双极型晶体管，Vdc为直流电压源，C 为一般无极性电容，VD1~VD8为续流二极管。

图5 四相不对称半桥功率变换器

根据法拉第电磁感应定律，开关磁阻电机的各绕组相电压平衡方程可以写成：

式中，Uk、Rk、ik、ek、ψk分别为k相绕组外加电压、电阻、电流、感应电动势、磁链；k=a,b,c,d。

由于转子位置角度是关于绕组相电感及电流的多元函数，根据式（4）、式（5），可将式（11）改写为：

式中，Lk为k相电感。

式（12）的首项为绕组相回路中的电阻下降，第2项为电流引起磁链变化的变压器电动势，第3项为转子位置改变引起磁链变化的运动电动势，与机电能量有关。结合上述分析，可以得到单相绕组电流励磁表达式为：

3 SRM气隙偏心电磁特性负效应分析

电机产生的不平衡径向电磁力和转矩波动作用于定、转子凸极之间，为探究气隙偏心条件下开关磁阻电机的径向电磁力与转矩空间特征，本文基于麦克斯韦应力张量法分析径向电磁力和转矩的空间电磁特性。

3.1 静态工况电磁力与转矩空间电磁特性

麦克斯韦应力张量法是计算开关磁阻电机电磁力的有效方法，它将磁场的有质动力归因于与磁力线方向一致的张力和垂直于磁力线方向的侧压力[21]。则开关磁阻电机定子凸极表面受到的径向电磁力Fr与切向电磁力Ft可写成：

式中，Br、Bt分别为磁通密度的径向分量和切向分量；μ0为真空磁导率；A为开关磁阻电机凸极表面s的面积。

设偏心绕组相电流为6 A，取定、转子凸极表面重合部分及邻槽部分路径积分求和，由式（14）可以得到极对极时刻。定子表面圆周径向电磁力如图6a 所示，当电机发生气隙偏心时，定子凸极一侧径向电磁力迅速增大，对称方向径向电磁力迅速减小，导致电机产生不平衡径向电磁力，如图6b所示。结合图6a、图6b可知，径向电磁力沿定子中心波动，且发生气隙偏心后，极小的气隙偏心增量将会产生大的径向电磁力波动幅值变化。

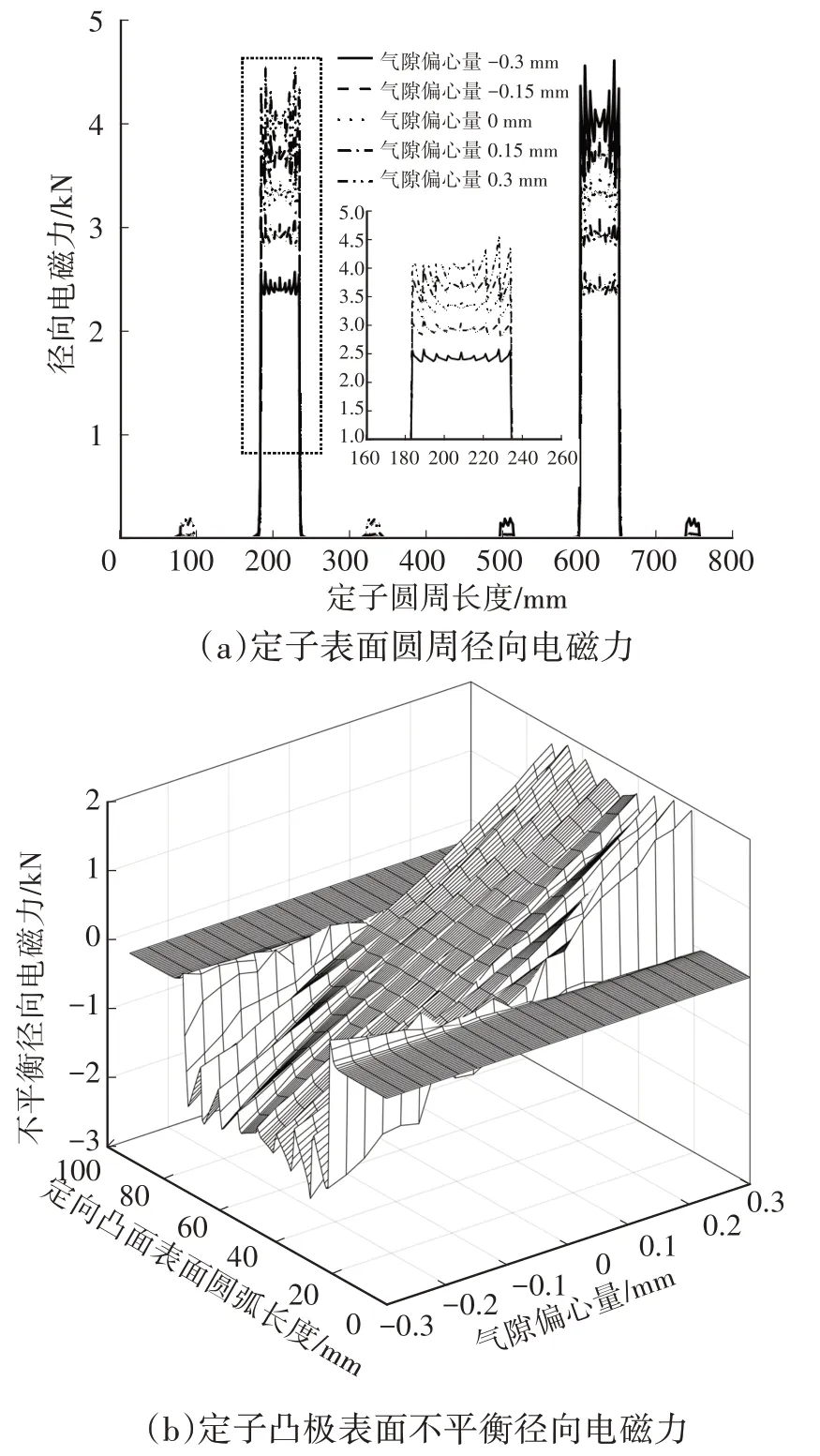
图6 SRM径向电磁力空间特性

另外，不平衡径向电磁力的大小和波动随着偏心量增大呈加剧趋势，证明电机在发生气隙偏心后，径向电磁力大小与波动量出现较大变化后，二者的耦合效应进一步加剧径向电磁力不平衡现象，无偏心情况下极对极时刻径向电磁力仿真相当于数值解析的误差为3.6%，验证了径向电磁力拟合式的有效性，可为后续轮毂电机驱动汽车动力学负效应研究提供理论基础。

此外，定子发生偏心导致气隙不均匀，对转矩也必将造成影响，由式（14）可以得到不同转子位置角度下的切向电磁力，如图7 所示，其中S1、S2分别为定子2个凸极的周向位置，S1、S2位置上、下波峰分别为定子与转子重叠部分边界产生的切向电磁力，与转子位置有关。从图7b 中可以看出：S1位置气隙减小0.3 mm 时，S1位置上波峰切向电磁力有所增大，下波峰切向电磁力反而减小，这是因为气隙减小时，径向磁密和切向磁密在不同转子位置角度下发生突变，造成切向电磁力有所增大或减小；S2位置气隙增加0.3 mm 时，径向磁密和切向磁密均减小，上、下波峰的切向电磁力均较无偏心时减小。

图7 SRM切向电磁力空间特性

基于上述分析，结合不同气隙偏心静态工况条件下的电磁转矩（如图8所示）可以验证切向电磁力变化对转矩的影响，由于切向电磁力作用于转子产生电磁转矩，电机定、转子产生相对位移后，电机转子凸极两端切向电磁力失衡，导致转矩发生相应变化。气隙偏心量的增加导致单相绕组转矩提高，在气隙偏心量保持不变的情况下，对称方向气隙偏心的转矩接近一致。

图8 SRM气隙偏心静态工况电磁转矩

3.2 瞬态工况电磁力与转矩分析

开关磁阻电机在实际应用于车辆时，轮胎在行驶过程中会受到路面冲击，造成电机定、转子之间的气隙发生变化，在开关磁阻电机瞬态工况下进行响应特性分析，更能够接近电机运行的真实情况。

其中，瞬态工况下的径向电磁力变化特性如图9所示，电机在瞬态工况下的电流高达25 A，且呈线性上升趋势，瞬态工况下径向电磁力呈现一定周期性，在定子和转子重叠开始至重叠结束过程中呈线性上升和下降，并且在偏心绕组相结束后出现微小波峰，由于下一相绕组通电，多余磁通量从偏心绕组相通过，产生径向电磁力。当气隙偏心量从-0.3 mm 变化到0.3 mm 时，径向电磁力最大值从5 172 N 增大至6 960 N，径向电磁力波动也随之加剧。

根据式（10）可以得到气隙偏心瞬态工况下的不平衡径向电磁力，如图10 所示，由于气隙偏心的存在，电机相对两极的径向电磁力差值不断增大，气隙的减小导致径向电磁力迅速增大，进一步增加电机相对两极方向径向电磁力的差值，导致电机产生净残余的不平衡径向电磁力，从图10 中可以看出，气隙偏心量为0.15 mm 时电机两极径向电磁力差值最大，为2 500 N，气隙偏心量继续增加至0.3 mm时差值为4 300 N。可以论证，气隙大小变化是影响不平衡径向电磁力的关键因素，所产生的不平衡径向电磁力以净残余力的形式继续加剧电机气隙偏心，不平衡径向电磁力将以周期性激励直接作用于轮毂电机驱动系统，影响车辆正常运行。

图10 SRM气隙偏心瞬态工况不平衡径向电磁力

综上所述，定、转子之间的气隙越小，所产生的电磁力越大。另外，气隙偏心瞬态工况下的电磁转矩如图11所示，由于开关磁阻电机瞬态电磁转矩由四相转矩合成而来，气隙偏心对竖直相位影响最大，对其余三相影响较小，但是这种现象将加剧开关磁阻电机转矩波动，进而产生周向激励造成电机振动，并以周期性激励持续作用于轮毂电机驱动系统，对于分布式驱动电动汽车，转矩波动将影响其纵向控制和横向控制性能。

图11 SRM气隙偏心瞬态工况电磁转矩

4 开关磁阻电机多目标优化设计

针对气隙偏心条件下不平衡径向电磁力和转矩波动电磁特性负效应问题，设定开关磁阻电机瞬态工况转速500 r/min及气隙偏心0.3 mm 作为初始条件，优化不平衡径向电磁力及其波动和电磁转矩波动。

4.1 优化方案制定

为了更好地量化不平衡径向电磁力波动特性，定义不平衡径向电磁力波动系数Fripple为：

式中，Fvmax、Fvmin、Fvave分别定子凸极所受不平衡径向电磁力的最大值、最小值和平均值。

同理，开关磁阻电机不平衡径向电磁力Fv定义为：

式中，Fui为不同采样点的不平衡径向力幅值；nf为采样数据数量。

通常，开关磁阻电机转矩波动系数Tripple可以定义为：

式中，Tvmax、Tvmin、Tvave分别为最大转矩、最小转矩和平均转矩。

进一步，为满足开关磁阻电机多目标优化需求，其目标函数可定义为：

式中，w1、w2、w3为权重因子，且w1+w2+w3=1；(Fripple)max、(Fv)max、(Tripple)max为所有采样数据中不平衡径向电磁力波动、不平衡径向电磁力和转矩波动的最大值；x为电机结构参数变量。

则由目标函数可以确定优化函数为：

式中，xopt为从参数变量中选取的最优结构参数。

基于优化函数对开关磁阻电机结构参数进行优化设计，变量参数范围如表2所示。

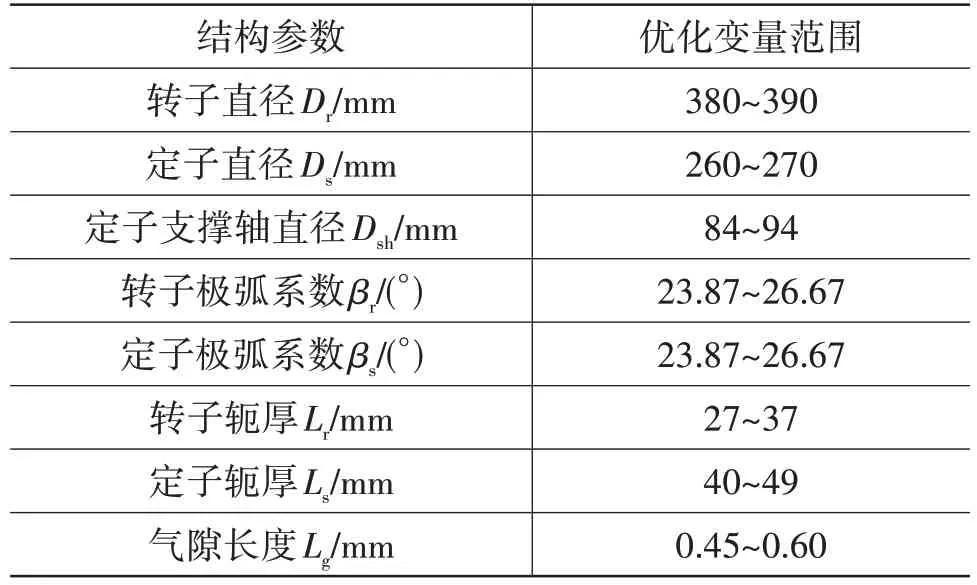
表2 结构参数优化设计变量范围

4.2 结构参数灵敏度分析

为分析开关磁阻电机结构参数对不平衡径向电磁力及其波动、电磁转矩波动的贡献权重，将结构参数变量范围均匀等分，构成最优拉丁超立方设计，各结构参数的灵敏度分析结果如图12所示。

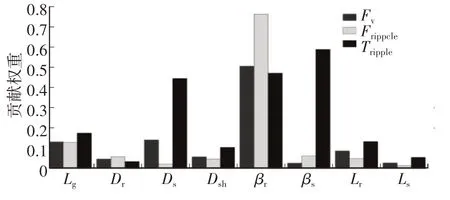
图12 结构参数贡献权重

在结构参数变量范围内，转子极弧系数对3 项优化目标的贡献权重最大，其中对不平衡径向电磁力波动的贡献权重为76%，定子外径与定子极弧系数对转矩波动贡献权重均超过44%，而对不平衡径向电磁力及其波动影响较小，其余各项结构参数对3项优化目标的贡献权重处于接近水平。

4.3 优化结果分析

基于优化目标函数设定2 种优化设计方案C1（w1=w3=0.3、w2=0.4）、C2（w1=0.3、w2=0.5、w3=0.2），采用第二代非支配排序遗传算法（Non-dominated Sorting Genetic Algorithms-Ⅱ，NSGA-Ⅱ）[22]对结构参数进行多目标寻优。考虑到电机在产生气隙偏心后所形成的不平衡径向电磁力对电机的影响远大于转矩波动对电机的影响，将C1 与C2 方案中转矩波动权重系数分别设置为0.4 和0.2，缩小转矩波动权重系数占比。通过设置3项优化目标的权重系数占比，实现各优化目标的优先级及相应优化效果。C1 方案权重系数的分配原则是3 项抑制目标均较好实现，C2方案权重系数的分配原则是以不平衡径向电磁力及其波动为主要抑制目标，将转矩波动权重系数占比缩小。

对开关磁阻电机结构参数进行多目标寻优，得到2种最优方案，其结构参数如表3所示。

表3 结构参数优化方案对比

根据表3 结构参数方案进行有限元仿真分析，得到不平衡径向电磁力及其波动、转矩波动和平均转矩响应结果如表4所示。

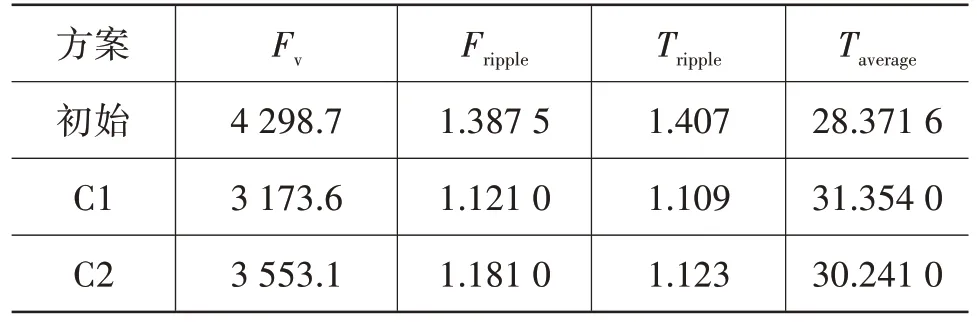
表4 优化结果仿真对比

2 种优化设计方案开关磁阻电机不平衡径向电磁力分别降低了26.2%和17.3%，不平衡径向电磁力波动分别降低了19.2%和14.9%，同时，转矩也得到改善，其平均转矩分别提升了10.5% 和6.6%，转矩波动降低21.2%和20.2%。为验证所设计的2 种优化方案在不同气隙偏心量下3 项抑制目标是否得到较好实现，对2 种优化方案进行不同气隙偏心量条件下的仿真分析。图13a 和图14a 所示为气隙偏心量为0.3 mm 时，2 种优化方案的不平衡径向电磁力和电磁转矩变化情况，其中针对不平衡径向电磁力，C1 方案的抑制效果优于C2 方案，C1 方案和C2 方案的最小转矩相同，并且C1 方案的最大转矩大于C2 方案的最大转矩，根据式（17）可知，C1 方案电磁转矩整体指标优于C2 方案。不平衡径向电磁力波动和转矩波动情况如图13b 和图14b 所示，从图13b 中可以看出，随着气隙偏心量的增加，C2 方案的抑制效果逐渐优于C1 方案。另外，在转矩波动优化方面，在气隙偏心量小于0.125 mm 时，2 种优化方案优化效果接近一致，在气隙偏心量大于0.125 mm 时，C1 方案优化效果逐渐优于C2 方案。

图13 不平衡径向电磁力多目标优化对比

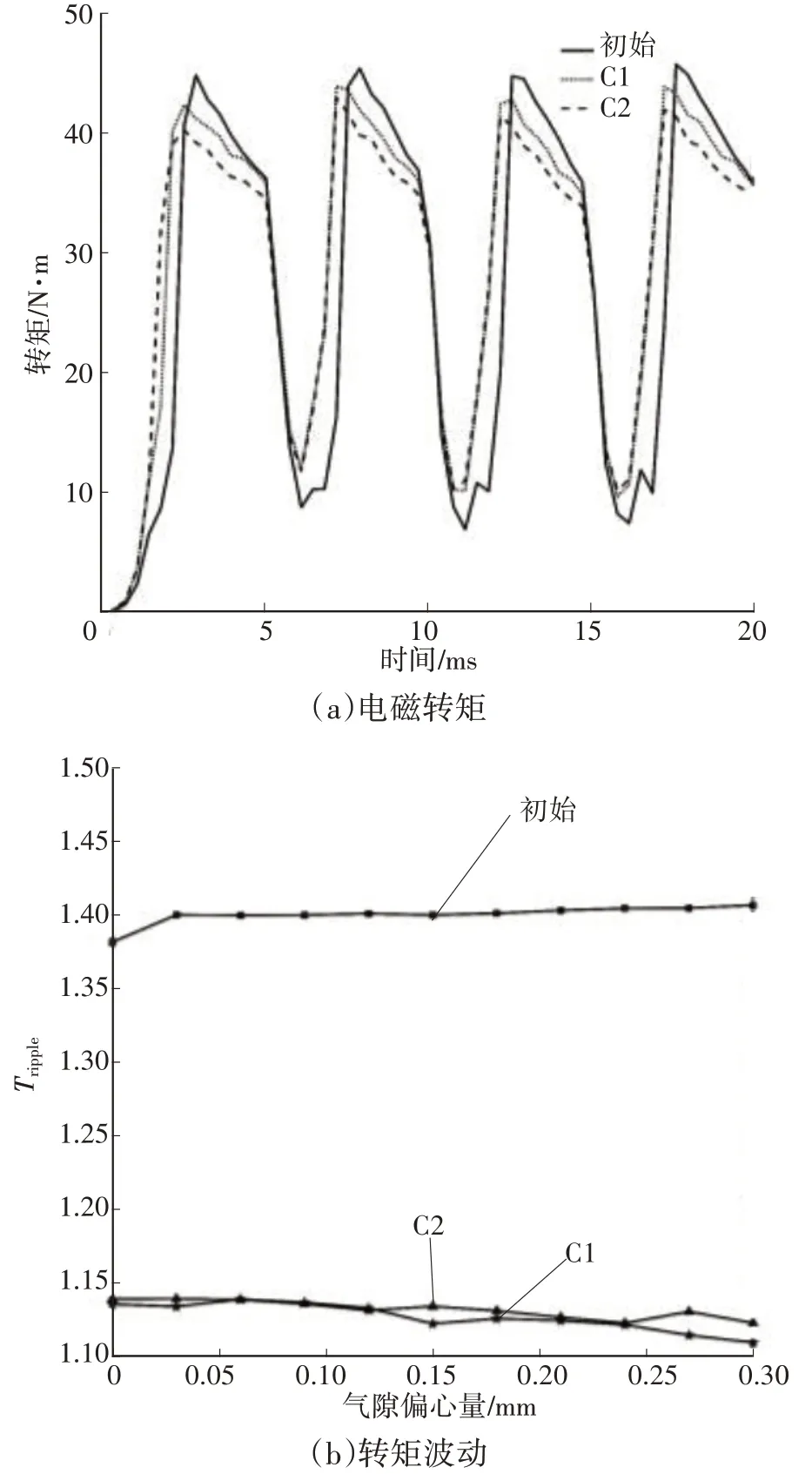
图14 转矩波动多目标优化对比

综上所述，虽然C2方案提高了不平衡径向电磁力波动权重系数占比，但其不平衡径向电磁力波动的整体抑制效果弱于C1 方案。C1 方案提高了转矩波动权重系数的占比，其优化结果整体优于C2 方案。由此可知，合理选择权重系数占比是抑制电磁特性负效应的前提条件。

5 结束语

本文以8/6 极开关磁阻电机为研究对象，分析了气隙偏心条件下开关磁阻电机的空间电磁特性，得到不同气隙偏心静态、瞬态工况下电机电磁特性响应特征，并采用多目标优化算法对其电磁特性负效应进行优化，得到以下结论：

a.轮毂开关磁阻电机发生气隙偏心后，径向电磁力将迅速变化，并产生不平衡径向电磁力，且随着气隙的减小，径向电磁力波动将加剧，气隙的增大使径向电磁力波动减弱，定子对称方向径向电磁力迅速变化导致不平衡径向电磁力波动趋势增大，转矩也随气隙偏心的增加而增大，且与气隙偏心方向无关。

b.瞬态工况下，由于换相期间存在其他绕组相干扰，气隙偏心对径向电磁力和不平衡径向电磁力恶化程度远大于静态工况，而电磁转矩方面，在2种工况下气隙偏心均会导致转矩增大，但对偏心绕组相转矩影响最大，对其他绕组相的转矩影响较小，这种特殊现象导致转矩脉动更加严重。

c.在提高开关磁阻电机性能的前提下，以不平衡径向电磁力、不平衡径向电磁力波动和转矩波动为优化目标进行结构参数寻优，不平衡径向电磁力、不平衡径向电磁力波动、转矩波动分别降低了26.2%、19.2%、21.2%，平均转矩提升了10.5%，轮毂开关电机各项输出参数均得到改善。