提升海上风电经柔直联网系统频率稳定性的协调控制策略

江守其，徐亚男，李国庆，辛业春，王丽馨

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林 吉林 132012）

0 引言

基于模块化多电平换流器的直流输电（modular multilevel converter based high voltage direct current，MMC-HVDC）技术具有控制速度快、运行方式灵活、供电可靠性高等特点，是实现深远海风电汇集和远距离外送的有效手段［1-2］。

海上风电经柔直接入受端电网的规模不断增大，部分同步机将逐步被替代，导致传统调频资源逐渐稀缺化，同时海上风电场侧交流频率与受端电网频率解耦，海上风电无法主动支撑受端电网频率，系统惯量逐渐降低，严重威胁其安全稳定运行。因此，如何实现海上风电场对受端电网频率变化的自主响应，消除电网发生扰动时引起的频率偏差，是提升系统频率稳定性亟待解决的关键问题。在惯量支撑方面，文献［3］通过远距离通信将受端电网频率波动的信号传递至风电场，通过调整其有功出力实现惯量支撑，但此方法存在延时问题，并且可靠性有待商榷。文献［4-5］针对海上风电经双端柔直联网系统，利用直流电压将频率信息传递至送端，通过送端换流站调整其交流侧频率，风电场根据系统频率调整其有功出力实现惯量支撑，但该方法将改变送端交流系统的频率质量，可能会给其他设备带来不利影响。文献［6-7］针对海上风电经多端柔直联网系统，提出了送、受端电压源换流器联合控制的频率下垂控制方法，通过直流电压传递频率信息，利用各换流站间的协调配合，实现受扰系统的惯量及频率支撑。文献［8］设计了一种适用于受端换流站的电压源型控制策略，在无锁相环情况下实现受端电网频率的自主响应，但其忽略了直流线路压降对频率信息传递精度的影响。文献［9］针对直流微电网，设计了基于观测器的直流电压控制策略，考虑了负荷及直流线路阻抗对其控制特性的影响，其是否适用于柔直输电系统有待进一步研究。

在频率偏差调节方面，目前研究主要集中于风电场参与一次调频方面，包括超速减载控制［10-11］、变桨控制［12-13］以及两者的协调控制［14］等，均是通过风机预留备用容量实现频率支撑。文献［15］提出了可整定风机静调差系数的频率控制策略，并与虚拟惯性控制有机结合，实现风机对系统频率的综合控制。文献［16］提出了海上风电场经多端柔直系统的顺序控制策略，按照网侧到风电场侧的顺序逐步启动调频设备，但未详细说明风电场具体的控制策略。为进一步提高频率响应能力，文献［17］提出了基于超级电容储能控制的虚拟惯量和一次频率控制策略，从而提高了单台风机的抗扰能力和主动支撑能力。文献［18］提出一种基于旋转备用加直流侧储能的风储联合控制策略，同时实现了风机的主动调频和故障穿越。上述文献仅关注采用单机聚合模型的风电场经柔直联网系统频率主动支撑问题，而针对综合考虑多台风机间响应能力差异的控制策略，以及风电场经柔直联网系统主动参与二次调频的研究较少。在加速构建新型电力系统的背景下，有必要进一步挖掘海上风电经柔直联网系统的调控潜力，使其整体成为主导电源，承担起支撑系统频率的责任。

在此背景下，本文针对基于双馈感应发电机（doubly-fed induction generator，DFIG）的海上风电经柔直联网系统，设计了提升系统频率稳定性的多时间尺度协调控制策略：①利用直流电容能量的同时，考虑不同风速下风机的响应能力差异，提出了基于直流电容电场能与DFIG 差异化转子动能的虚拟惯量协调控制；②计及直流电压与DFIG转子转速约束，设计了考虑变速控制与桨距角控制响应差异的一次调频协调控制，并对相关控制参数进行了设计；③基于直流电压与受端电网频率的耦合关系，提出了风电场主动消除直流电压偏差量的附加桨距角控制。最后，通过仿真验证了所提控制策略的可行性。

1 海上风电经柔直联网系统结构

海上风电经柔直联网系统结构如图1 所示。系统采用对称单极接线方式，其中：风电场侧的送端换流站（wind-farm-side sending-end modular multilevel converter，WFMMC）采用定交流电压控制和定频率控制，以稳定海上风电场的并网母线电压和频率；网侧受端换流站（gird-side receiving-end modular multilevel converter，GSMMC）通常采用定直流电压控制和定无功功率控制，以保证直流电压的稳定。随着海上风电渗透率的不断增大，受端交流电网呈现越来越明显的低惯量、弱阻尼特性，在传统同步发电机组备用计划无法满足电网调频容量和速度需求时，可能导致电网频率变化率大、频率越限等问题。因此，亟需挖掘海上风电功率调节潜力，使其主动支撑系统惯量、参与频率稳定调控，提升系统的安全稳定性。

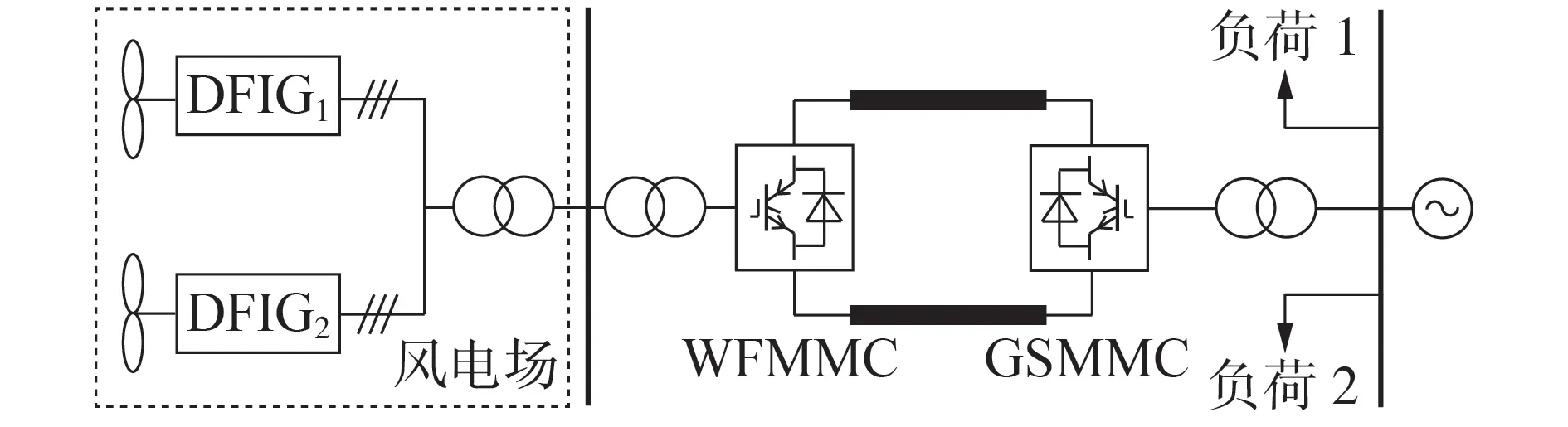
图1 海上风电经柔直联网系统结构Fig.1 System structure of MMC-HVDC connecting offshore wind power

2 虚拟惯量控制策略

爱因斯坦狭义相对论表示：惯性是能量的固有属性，能量具有惯性，任何惯性都应归因于能量［19］。因此，为了抑制受端交流电网不平衡功率引起的频率突变，本文设计了一种基于直流电容能量与DFIG转子动能的虚拟惯量控制策略，在受端电网频率突变时共同为系统提供惯量支撑。

2.1 基于直流电容储能的虚拟惯量控制

同步机的惯量响应过程可描述为：

式中：H为同步机的惯性时间常数；f为交流电网实际频率；PM为机械功率；PE为电磁功率。

模块化多电平换流器（modular multilevel converter，MMC）直流侧的等效电容可利用其动态特性起到抑制直流电压变化的作用，即在忽略线路有功损耗的情况下，利用直流电压的变化反映整流侧与逆变侧之间的功率不平衡关系，如式（2）所示。

式中：Ceq为MMC 的等效电容［20］；Udc为实测的直流电压；Pwind为风电场的输出功率；Pgrid为传递到网侧的有功功率。

为了使MMC 具备同步机的惯量响应特性，类比式（1）所示的同步机惯量响应过程，Pwind可看作同步机的机械功率，为了方便控制策略设计，在仅考虑直流电容为系统提供惯量支撑时可先假设Pwind为常量；Pgrid可看作同步发电机的电磁功率，则直流电压的变化可类比于同步机转速的变化，主要区别在于直流电容是利用其自身能量为系统提供虚拟惯量支撑，进而抑制频率突变；同步机则是利用其转子动能提供惯量支撑，直接决定系统频率。结合式（1）、（2）可得：

式中：Udc0为稳态下的额定直流电压；ΔUdc=Udc-Udc0为直流电压的偏差；f0为交流电网额定频率。

为保证系统的安全稳定运行，通常将直流电压偏差量限制在较小范围（±5 % 左右）内，故可忽略电压偏差的二次项，结合式（5）可得：

式中：Δf=f-f0为交流电网的频率偏差；kc为直流电压偏差量与频率偏差量之间的耦合系数。

由式（6）可知，通过将受端电网频率偏差引入GSMMC 直流电压控制环节，如式（7）所示，可建立直流电压与频率之间的耦合关系，使其主动参与电网频率调节的同时将频率波动信息传递至直流侧，为风电场主动支撑惯量提供响应条件。

式中：Udcref为GSMMC定直流电压参考值。

由式（7）可知，ΔUdc与Δf之间的耦合系数kc越大，Udcref越大，越易达到直流电压限值，导致直流电压无法传递完整的受端电网频率信息。因此，可根据允许的直流电压最大偏差值ΔUdcmax与允许频率波动的上限值Δfmax，设计kc的取值为：

2.2 基于DFIG转子动能的虚拟惯量控制

受直流电压偏差约束限制，直流电容所能提供的能量较少，惯性作用有限，可结合DFIG 的转子动能进一步增强惯量支撑作用，使其在电网频率突变时，能够存储或释放转子动能，主动提供惯量支撑。针对不同风速下的风机，通过引入本地直流电压变化率设计了一种基于差异化转子动能调节的风电场虚拟惯量控制策略，其无需远距离通信即可改变风电场的有功出力，有效提高系统抑制频率突变的能力。风电场主动支撑系统频率的控制策略如图2所示。图中：ωopt为最优转速；ΔUdcth为直流电压死区限值；vw为风速；β为桨距角；kp为转速调节量与直流电压偏差量之间的耦合系数；kd为转速调节量与直流电压变化率之间的耦合系数；Td为惯性环节时间常数；kpitch为桨距角调控环节比例系数；kβ为电压型附加桨距角控制中的耦合系数；Pref为有功功率参考值；Pn为额定功率；PI为比例积分（proportional integral，PI）控制器。

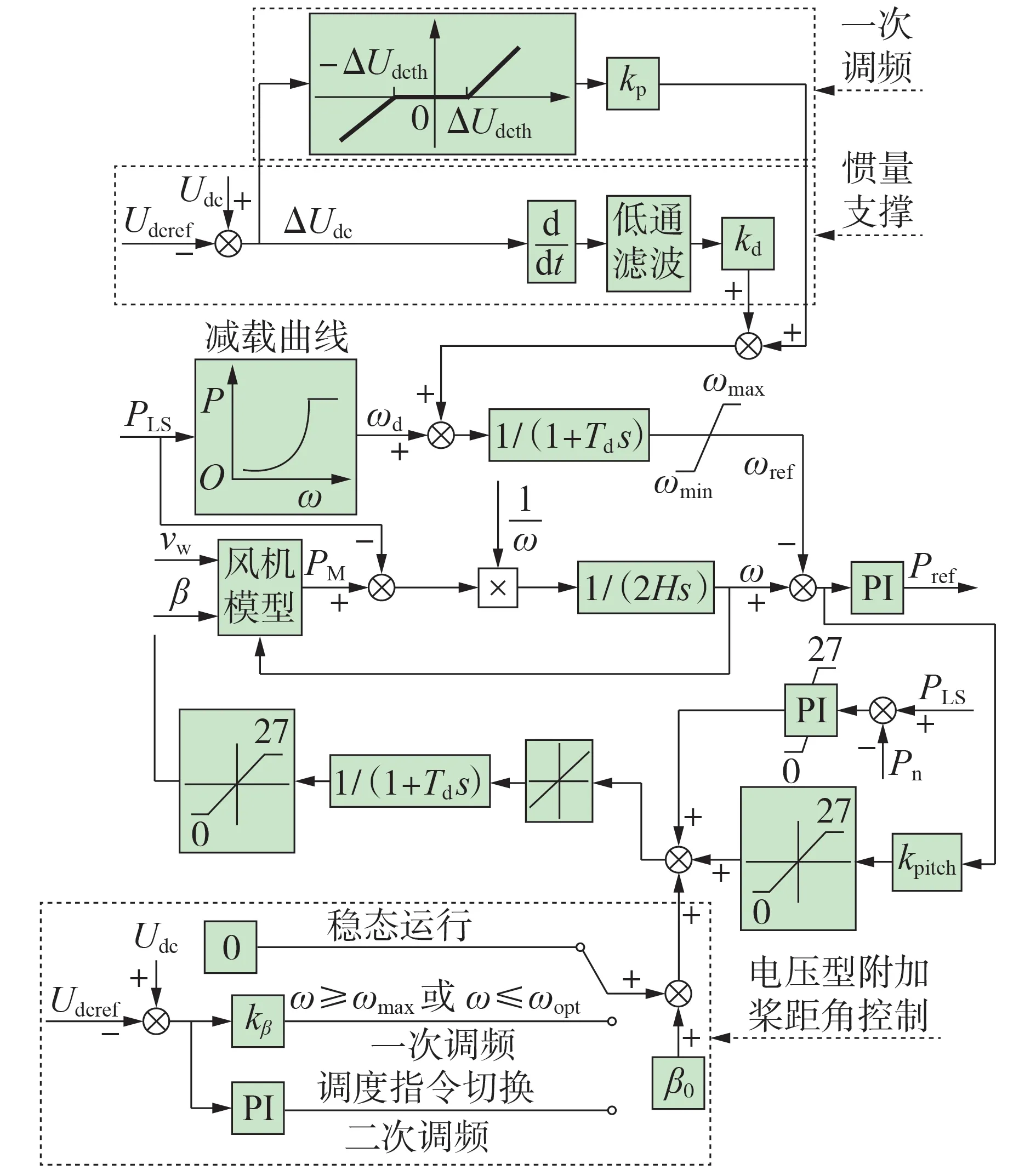
图2 风电场主动支撑系统频率的控制策略Fig.2 Control strategy of wind farm actively supporting system frequency

2.2.1 虚拟惯量控制策略设计

当系统受到扰动时，利用式（7）所建立的直流电压与电网频率耦合关系，将电网频率波动信息以直流电压为载体传递至风电场侧，将WFMMC 侧直流电压的变化率dUdc/dt引入风电场各DFIG 有功控制环节，使其主动改变有功出力响应受端电网频率突变，为系统提供惯量支撑。

为了使海上风电场能够同时满足不同频率变化情况下的频率调节需求，通常预留一定的功率备用，使其稳态运行于超速减载模式［14］。设DFIG 超速减载后的功率跟踪曲线方程为：

式中：kLS为减载功率跟踪系数；ωd为当前转速。

当受端电网频率升高时，直流电压将实时联动上升，各DFIG 根据dUdc/dt改变其转速参考值，快速降低风电场输出功率，如式（11）所示，由于转速调节量Δω通常不大，在此忽略了二次项（Δω）2和三次项（Δω）3。结合式（2）与式（11），DFIG 减少有功出力ΔPwind的过程可类比为一个虚拟电容提供惯量支撑的过程，即DFIG通过转子动能为系统提供虚拟惯量支撑，如式（12）所示，进而可得Δω与dUdc/dt的关系如式（13）所示。

式中：ΔCvir为直流侧附加虚拟电容。

图3 为风机主动提供惯量支撑的示意图（图中风机功率和转速均为标幺值），DFIG 稳态运行于减载点B，在受端电网频率上升初期，不平衡功率最大，利用所提虚拟惯量控制可使DFIG 快速、大幅度降低其输出功率，输出功率减少值为ΔPgrid，此过程如图3中点B至点C红色箭头所示，有效降低频率上升率。此时DFIG捕获的机械功率大于电磁功率，转子转速上升并通过存储动能为系统提供惯量支撑；随着转速上升机械功率将逐渐减少，如图3 中ΔPwind所示，同样可以抑制频率上升，呈现出类似同步发电机的阻尼特性。在受端电网同步发电机一次调频作用后，系统的频率偏差将逐渐趋于定值，并且dUdc/dt随之变为0，风机不再提供惯量支撑，重新恢复到扰动前稳态运行点，此过程如图3中点D至点B红色箭头所示。

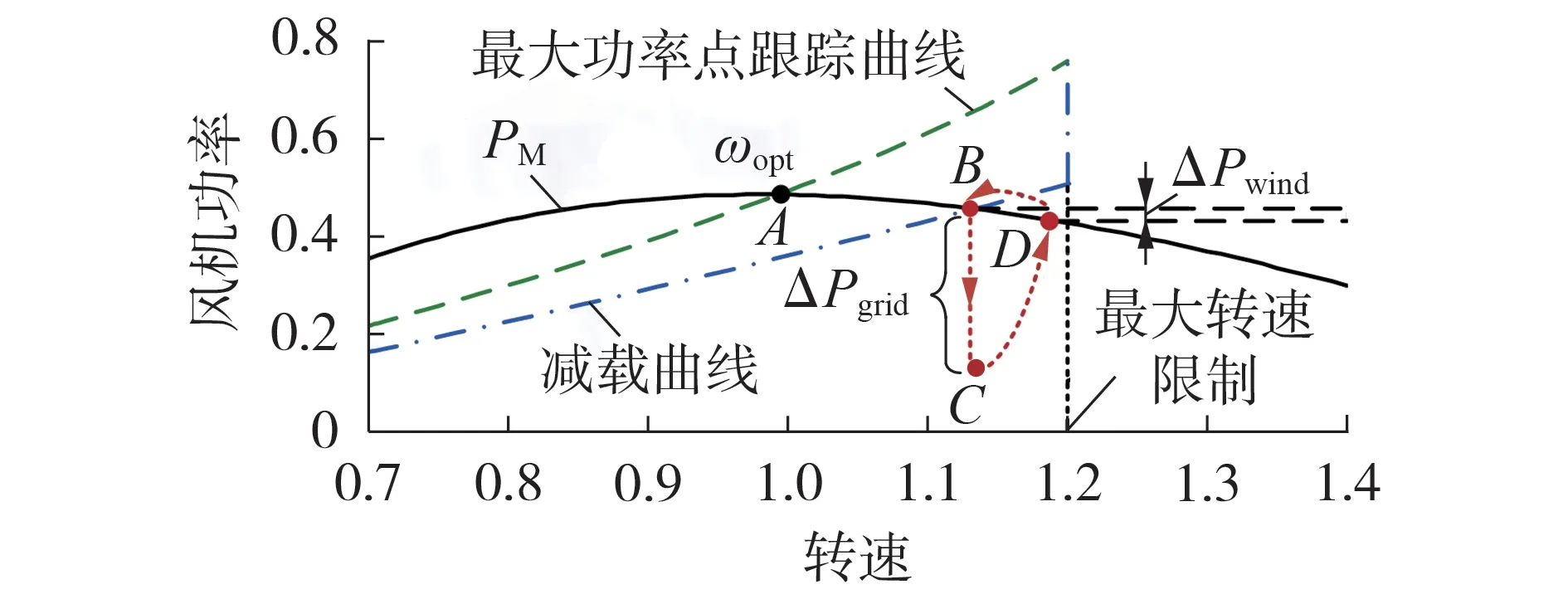
图3 风机功率特性曲线Fig.3 Curves of wind turbine power characteristic

综合上述分析可知，考虑海上风电场主动支撑系统惯量后，式（2）可进一步修改为式（14），即风电场能够通过增大柔直系统等效电容增强其惯性作用，实现其转子动能与直流电容能量共同提供惯量支撑，增大其等效惯性时间常数，如式（15）所示，从而抑制频率突变，提升系统频率稳定性。由于受端电网频率下降时的惯量响应过程与上述类似，在此不再赘述。

式中：HS为系统的虚拟惯性时间常数。

2.2.2 控制参数设计

稳态运行时DFIG 转子转速距离最大转速（或最优转速）越近，其转速可变化的空间越小，可存储（或释放）的转子动能越少；反之，则越多。因此，需根据DFIG变速控制启动时的转速ωd0合理设计kd，以充分利用各DFIG 的转子动能，实现虚拟惯量的协同响应。

由图3 可知，DFIG 转子运行于最优转速ωopt时，DFIG 捕获的机械功率达到最大值，且能够发挥最大的阻尼作用，故当扰动引起电网频率跌落时，为了更快地抑制频率跌落，DFIG 转速可下降的最小值为ωopt；而当扰动引起电网频率上升时，DFIG 通过增大转速以存储动能，转速可上升的最大值为ωmax，故本文将DFIG 转速的可调节范围设计为［ωopt，ωmax］。根据式（6）和式（13）可知，Δω与dUdc/dt（即频率变化率df/dt）成正比，为了防止df/dt过大损坏机组，在设计参数kd时需同时考虑Δω和df/dt的限值约束。

基于dUdc/dt与df/dt的耦合关系，在频率上升时，考虑直流电压变化率的最大值约束max（dUdc/dt）与ωmax之间的对应关系如式（16）所示；同理可得频率下降时max（dUdc/dt）与ωopt之间的对应关系。综上可得耦合系数kd的取值如式（17）所示。

由式（17）可知，各DFIG 可根据ωd0合理选取其kd，实现不同风速下各DFIG 转子动能的差异化利用，有效提高了风电场的惯量支撑能力。

3 频率主动支撑控制策略

由于直流电容与DFIG 转子提供惯量支撑的过程是短暂且不可持续的，仅可抑制扰动初期的频率突变，为了维持受端电网频率在安全范围内，需要风电场具备主动参与系统调频的能力，从而降低系统频率偏差，保证其安全稳定运行。本文基于式（7）建立的频率与直流电压耦合关系，分别设计了海上风电经柔直联网系统参与一次调频和二次调频的控制策略，以提升频率支撑能力。

3.1 一次调频控制策略

为了实现与同步机类似的调频功能，基于本地直流电压测量信息，设计了考虑变速控制与桨距角控制响应差异的风电场一次调频协调控制策略。通过将直流电压的偏差量ΔUdc引入风电场各DFIG 有功控制环节，调整DFIG 的有功出力，实现风电场主动参与一次调频，从而提升受端交流电网的频率稳定性。

3.1.1 基于变速控制的一次调频

当直流电压达到其死区限值ΔUdcth时，DFIG 立即通过改变转速来调节其所捕获的机械功率，实现风电场主动参与一次调频。结合式（12）可知，受端电网频率偏差量Δf以直流电压偏差量ΔUdc的形式传递至风电场，且满足Δf∝ΔUdc∝Δω∝ΔPwind，如式（18）与式（19）所示。若风电场一次调频后转速在其允许的调节范围内，则DFIG将稳定运行于新的平衡状态。

式中：η为调压系数。

为了实现风电场一次调频功率的合理分配，类比2.2.2 节的思想，结合式（16）和式（17），可得ΔUdc与Δω之间的耦合系数kp取值为：

3.1.2 基于桨距角控制的一次调频

当DFIG转子转速达到ωmax（或ωopt）时，即基于变速控制的一次调频能力达到上限，通过控制其转子转速不变，维持DFIG 变速控制的调频能力，并启动图2 中基于电压型附加桨距角控制的一次调频模式，通过将直流电压偏差量产生的附加桨距角Δβ叠加至初始备用桨距角β0，进一步改变风电场的有功出力，从而实现DFIG变速控制与附加桨距角控制参与一次调频的协调配合。类比2.2.2 节的思想，图2中电压型附加桨距角控制中的耦合系数kβ可定义为：

3.2 二次调频控制策略

随着海上风电等新能源渗透率不断提升，传统同步发电机将逐渐被替代，系统调频能力将明显降低，消除频率偏差的能力也将减弱，频率稳定问题可能成为我国电力系统低碳化转型路径上的重要瓶颈。相比惯性和一次调频抑制频率波动的过程，二次调频是在更长时间尺度内实现频率动态平衡，可提高整个系统的稳定性和抗扰性。因此，本文进一步挖掘了大规模海上风电经柔直联网系统的二次调频潜力，根据本地直流电压测量信息，设计了基于附加桨距角控制的二次调频策略，使其整体呈现主导电源的特性，提高受端电网的频率稳定性。

由于受端电网频率偏差与直流电压直接耦合，将电压型附加桨距角控制中的二次调频控制目标设置为柔直系统GSMMC 定直流电压参考值Udcref（忽略线路损耗），在接收到调度指令后，使其主动参与柔直系统直流电压调节，消除其稳态偏差量，进而实现受端电网频率的无差调节。在风电场参与一次调频后，电网频率偏差趋于定值，若此时DFIG 转子转速未达到其限值ωmax（或ωopt），在接收到调度指令后，直流电压偏差量通过比例积分环节产生附加桨距角Δβ，仅通过改变桨距角调整风电场有功出力，消除一次调频后仍存在的频率偏差，实现与同步机类似的二次调频功能，同时使转子转速恢复至初始转速，恢复风电场的惯量支撑能力；若DFIG转子转速已达到其限值ωmax（或ωopt），则表示不平衡功率较大，需维持其转速不变，即维持变速控制的调频能力，再通过二次调频作用进一步调节其桨距角，使变速控制和桨距角控制共同承担系统不平衡功率，维持直流电压稳定，在充分利用风电场功率调节能力的同时实现受端电网频率的无差调节。

综合上述分析，设计了多时间尺度频率支撑协调控制策略的实施流程如图4 所示，可有效提升海上风电经柔直联网系统的频率稳定性。

4 仿真验证

在MATLAB／Simulink 中搭建了图1 所示海上风电经柔直联网系统模型，并利用RT-LAB OP5600进行仿真。其中海上风电场的总容量为1 500 MW（由2 台DFIG 单机聚合模型组成），受端电网中2 台同步机组的容量均为900 MW，送、受端换流站的主要参数如附录A 表A1 所示。下面将以切负荷的情景为例，分别对虚拟惯量控制和调频控制策略的有效性进行仿真验证。

4.1 虚拟惯量控制策略的仿真验证

系统稳态运行时，WFMMC 汇集646 MW 的风电场输出功率，其中风电场内DFIG1和DFIG2风速分别为9、10 m／s，受端电网的负荷1 为2 070 MW，负荷2 为200 MW，为了验证扰动下所提虚拟惯量控制策略的有效性，t=50 s 时将负荷2 切除，受端电网频率迅速上升。为了更好地验证本文所提控制策略的有效性，分为以下情景进行仿真对比验证：①情景1，未采用任何附加控制；②情景2，仅利用直流电容提供惯量支撑；③情景3，采用本文所提虚拟惯量控制。对比结果如图5所示。图中：PSG为同步机功率，PDFIG1、PDFIG2和ωDFIG1、ωDFIG2分别为风电场内DFIG1、DFIG2输出的有功功率和转速，以上变量均为标幺值，后同。

图5 虚拟惯量控制前、后系统暂态响应结果Fig.5 Transient response results before and after virtual inertia control

根据仿真结果可以看出，当切除负荷2 引起电网频率上升时，情景2、3 中的直流电压也随之上升，直流电容主动支撑系统惯量，但仅能短暂提供少量的惯量支撑，故情景1、2 中电网频率突变程度相近，而情景3 中DFIG 转子可提供更多的惯量支撑，其频率突变程度较为缓慢。惯量支撑仅发生在频率突变初期，在频率偏差大于同步机组一次调频死区后，将降低其有功出力，最终维持系统功率平衡，可以看出情景3 中同步机的输出功率下降速率及幅度均较小，表明DFIG利用转子动能和捕获风功率的变化能够为系统提供较大的惯量支撑和阻尼作用。在DFIG 主动支撑系统惯量过程中，稳态运行时风速低的DFIG 转速变化较大，即存储了更多的转子动能，实现了DFIG转子动能差异化利用，有效提高了海上风电的惯量支撑能力。

4.2 频率主动支撑控制策略的仿真验证

为了验证所提调频控制策略的有效性，根据电网一次调频启动阈值±0.033 Hz 设计风电场一次调频电压启动阈值，初始桨距角β0=2°，仿真工况与4.1节相同。从以下3 个情景进行仿真对比验证：情景4，仅同步机参与一次调频；情景5，DFIG仅采用变速控制与同步机共同参与一次调频；情景6，在情景5一次调频的基础上启动附加桨距角控制的二次调频模式。仿真对比结果如图6所示，图中βDFIG1、βDFIG2分别为风电场内DFIG1和DFIG2的桨距角。

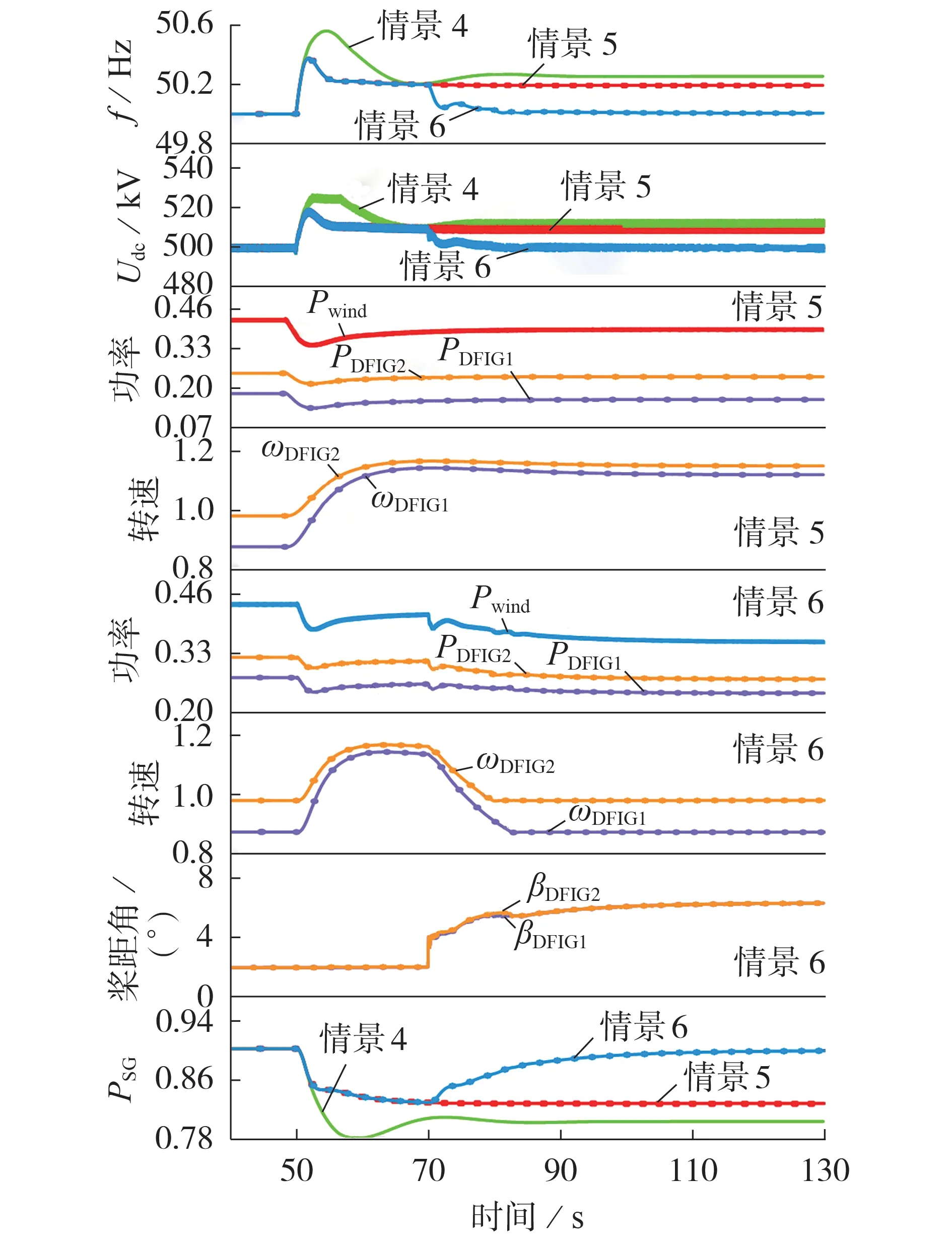
图6 风电场调频控制前、后系统暂态响应结果Fig.6 Transient response results before and after frequency regulation control of wind farm

根据仿真结果可以看出，当负荷2 被切除后，受端电网频率上升，其频率信息通过直流电压传递至风电场，此时启动DFIG 的变速控制参与一次调频，故情景5比情景4的电网频率能更快地恢复稳定，风电场在实现对电网频率自主响应的同时起到了抑制直流电压的作用。风电场通过增大转子转速以降低其有功出力，从而实现一次调频。一次调频后受端电网仍存在频率偏差，在70 s时启动二次调频，通过增大桨距角进一步降低风电场内各DFIG 的输出功率，在消除受端电网频率偏差的同时恢复DFIG转子转速至初始转速，从而恢复其惯量支撑能力。调频期间，风电场启动变速控制后，情景5 中同步机输出功率的下降幅度变小，缓解了同步机参与一次调频的压力；风电场启动附加桨距角控制后，逐渐消除受端电网的频率偏差，情景6 中同步机输出功率也逐渐恢复至初始值，从而验证风电场具备二次调频的潜力。

为了进一步验证基于变速控制与附加桨距角控制协同的DFIG 调频能力，设定与送端换流站相连的DFIG1和DFIG2风速分别为10.5 m／s 和11 m／s，受端交流系统连接的负荷1 为2 330 MW，负荷2 为250 MW，50 s 时将负荷2 切除，DFIG 优先利用变速控制参与一次调频，并依次切换至附加桨距角一次调频和二次调频模式，仿真结果如附录A图A1所示。

当负荷2 被切除，DFIG 通过超速减载和同步机组共同参与一次调频时，DFIG 转子转速达到上限值，且电网频率仍在上升，54 s 时启动附加桨距角控制的一次调频模式，并维持DFIG转子在最大转速运行，进一步增大DFIG 的一次调频能力，使电网频率更快地恢复稳定。一次调频后，电网频率偏差趋于定值，80 s 时切换至附加桨距角控制的二次调频模式，使风电场根据直流电压偏差进一步增大其桨距角，降低有功出力，从而消除一次调频后的频率偏差，实现类似于同步机的二次调频功能。

为了使海上风电场能够同时满足不同频率变化情况下的频率调节需求，进一步验证本文所提协调控制策略在频率下降工况中的有效性，50 s 时增加负荷100 MW，仿真结果如附录A图A2所示。

当受端电网负荷增加时，电网频率快速下降，在风电场频率主动支撑控制作用下，其输出功率增加，此时风电场的输出功率大于其捕获的机械功率，DFIG 转子将减速释放动能，并提升其捕获机械功率，与同步发电机一次调频共同承担不平衡功率，有效降低电网频率下降速率及幅度，使系统频率逐渐趋于稳定。70 s 时维持DFIG 转速不变，使DFIG 启动附加桨距角二次调频控制，进一步承担系统不平衡功率，直至频率恢复至扰动前的稳态值，实现无差调节，有效验证了海上风电经柔直联网系统在不同频率变化工况下的频率主动支撑能力。

5 结论

针对新型电力系统构建过程中传统调频资源逐渐稀缺化的问题，本文提出了适用于海上风电经柔直联网系统虚拟惯量控制、一次调频和二次调频的协调控制策略及参数选取方法，使其整体呈现主导电源特性，能够为系统提供必要的惯量及频率支撑。通过仿真分析得出如下结论：

1）在惯量支撑方面，利用直流电容能量提供惯量的同时建立了直流电压与频率的耦合关系，风电场根据本地直流电压变化率和当前转速即可实现不同DFIG转子动能的差异化利用，在充分利用惯量支撑及阻尼能力的同时有效抑制了扰动初期电网的频率变化；

2）在频率偏差调节方面，通过将直流电压偏差引入DFIG变速控制和桨距角控制，结合了两者频率响应速度及能力，使风电场具备传统同步机的一次调频和二次调频功能，有效提升了系统的频率稳定性。

值得指出的是，基于直流电压改变海上风电输出功率，可在实现电网频率主动响应的同时增强柔直系统直流电压变化的惯性和阻尼作用，故本文所提控制策略可为盈余功率引起直流过电压的故障穿越问题提供新的解决思路。

附录见本刊网络版（http：//www.epae.cn）。