渭河上游水沙变化特征分析

唐骄宇 卢 洋

(1.长安大学,陕西 西安 710000;2.黄河水利委员会三门峡库区水文水资源局,河南 三门峡 472000)

渭河流域为干旱半干旱区域,在气候变化和人类活动的影响下,渭河上游降水、径流和泥沙均有不同程度的变化。渭河上游流域下垫面为黄土沟壑,水土流失严重,水资源供需矛盾突出,降水、径流和泥沙的年际和季节变化规律对于研究地区水资源开发利用有重要影响。因此,研究区域内降水、径流、泥沙变化规律,为渭河上游防汛抗旱、生态环境保护、水资源规划和开发利用提供技术支撑,对于分析水循环规律、预测极端水文事件等具有重要意义。

本文以渭河上游天水水文勘测区(以下简称“天水测区”)为研究区域。天水测区上起渭河武山,下至天水市麦积区东岔镇,包括区间支流散渡河、葫芦河、藉河、牛头河流域,测区内有黄土高原、秦岭、六盘山,年降水量地域分布极不均匀。采用的水文资料系列为1990—2020年,年降水量采用测区各雨量站实测数据,据此计算出流域平均面雨量;年径流量、年输沙量采用北道水文站实测值,利用线性趋势法、肯德尔秩次检验法、启发式分割、有序聚类法、季-海哈林法、双累积曲线法等方法研究了降水、径流和泥沙的变化特点、趋势性、突变性,进而分析变化的影响原因,分析成果可为流域水资源合理开发利用与配置提供参考。

1 分析计算方法

1.1 趋势性分析

分别采用线性回归法、非参数检验法、肯德尔秩次检验法等进行趋势性分析。

1.1.1 线性回归法

线性回归法构建水文变量x与其时间t的一元线性回归方程:

x(t)=a+bt

(1)

回归系数b的显著性可通过t检验进行判断,构建的T统计量:

(2)

服从自由度为(n-2)的t分布,给定显著性水平α,可查得tα/2,如果T>Tα/2,则认为回归效果显著,存在线性趋势;否则,线性趋势不显著。

1.1.2 非参数检验法

非参数检验法是对原始数据的秩进行分析,不需要样本服从一定的分布,根据样本信息对总体分布情况进行推断和处理,并针对其不同条件下的参数进行优化和整理。

1.1.3 肯德尔秩次检验法

利用肯德尔秩次检验法(Mann-Kendall法,简称M-K)[1]对水文序列的趋势性采取显著性检验方式,是一种非参数方法(亦称无分布检验),其优点是样本不需要遵从一定的分布,也不受少数特异值的干扰,计算过程相对简单,被广泛应用于水文变量、要素等非正态分布的趋势分析中,计算出相应的检验值,对水文序列的趋势性和突变性进行有效的检验,其原理见表1。

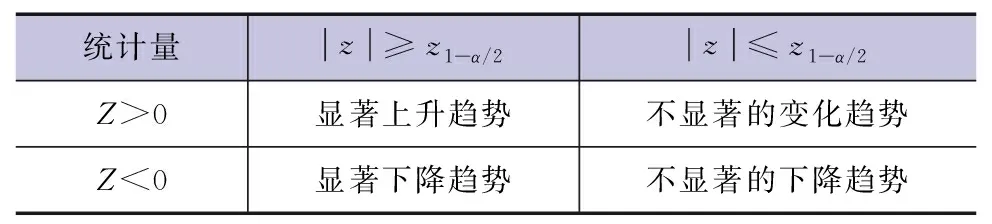
表1 M-K趋势判断表(显著性水平α=0.05)

时间序列X以(X1,X2,X3,…,Xn)表示,建立标准正态分布统计量Z:

(3)

其中

(4)

(5)

(6)

式中:当n>10时,s为近似服从正态分布;Var(s)为方差;m为数据相同的组数;tk为与第k组的数据相同的个数。

给定显著性水平α,依据表1可以判断序列的上升或下降趋势显著情况。

以Kendall倾斜度β量化序列,β可表示为

(7)

式中:l0时,呈现上升趋势,反之呈下降趋势。

1.2 跳跃成分分析

跳跃成分分析分别采用有序聚类法、季-海哈林法、启发式分割法对降水、径流进行突变点诊断,年输沙量除采用前述三种方法外,还采用了双累积曲线法进行突变点诊断分析。

1.2.1 有序聚类法[2]

有序聚类法利用最优分割点来推求突变点,基本原则是使同要素之间的离差平方和较小。设有水文序列x1,x2,…,xn,假设可能的突变点为τ(2≤τ≤n-1),则突变点前后的离差平方和分别为

(8)

(9)

有序聚类法常用的目标函数为

(10)

当式(10)中S取极小值时,对应的τ为最优分割点,可推断为突变点。

1.2.2 季-海哈林检验法[2]

对于水文时间序列x(t),假定总体为正态分布,且可能变异点τ的先验分布为均匀分布的情况下,推得τ的后验分布为

(1≤τ≤n-1)

(11)

(12)

式中:k为比例常数;n为样本容量。当统计值f(τ)取最大值时,满足后验分布条件,此时对应的τ值为最可能分割点,由此确定最可能变异年份。

1.2.3 启发式分割法

相关研究[3-4]表明启发式分割能在不同时间尺度高效地把非平稳时间序列划分成多个不同均值的子序列,并且相比多种常用突变检测方法,能有效地排除虚假的变异点。对于时间序列X[X1,X2,…,Xn],其各点的合并偏差可采用下式计算:

(13)

式中:SD为合并偏差;N1、N2分别为该点左边部分和右边部分的点数;S1、S2分别为该点左边部分和右边部分的标准差。各点的统计量T计算公式为

(14)

式中:μ1、μ2分别为该点左边部分和右边部分的均值。

统计量T最大值Tmax的置信度P(Tmax)的计算式为

P(Tmax)≈{1-I[v/(v+Tmax2](δv,δ)}η

(15)

当P(Tmax)达到指定的置信度时,则该点为显著的均值突变点,对原序列进行分割,之后对分割后的子序列继续检测。若P(Tmax)未能达到指定的置信度区间,则不再分割。

2 计算结果分析

2.1 降水

2.1.1 降水趋势变化

天水测区平均年降水量年际变化见图1,其多年平均年降水量为534.9mm,最大为755.4mm(2003年),最小为361.2mm(1997年)。年降水量趋势线表明31年来降水总体呈平稳微弱上升趋势。线性回归法、非参数检验法、肯德尔秩次检验法均一致诊断为趋势不显著,但计算检验值与标准值较接近(见表2),说明上升与非上升趋势处于临界状态。

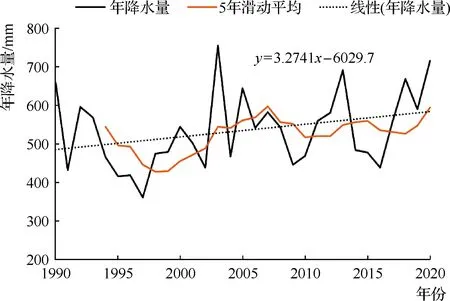
图1 天水测区年降水量年际变化

表2 天水测区年降水量序列趋势诊断结果

2.1.2 降水突变点诊断

对测区平均年降水量进行M-K突变检验,并设置0.05显著性水平,即得到置信区间,临界值为-1.96和1.96,分析结果见图2。根据分析,年降水量UF、UB曲线在2010年后出现多个交点,相交于置信期间内,且两曲线趋势一致,通过UB、UF交叉点可知,突变点在2017年前后。

图2 天水测区年降水量M-K秩次检验

采用有序聚类法和季-海哈林法进行同步验证,得出相同检验值,|T|=2.42,T(0.05/2)=1.96,|T|>T(0.05/2),根据检验值趋势图,有序聚类法分析出其2017年资料系列达到最小值,季-海哈林法分析出其2017年资料系列达到最大值,根据突变点判别,在2017年前后均值发生显著跳跃,见图3、图4。

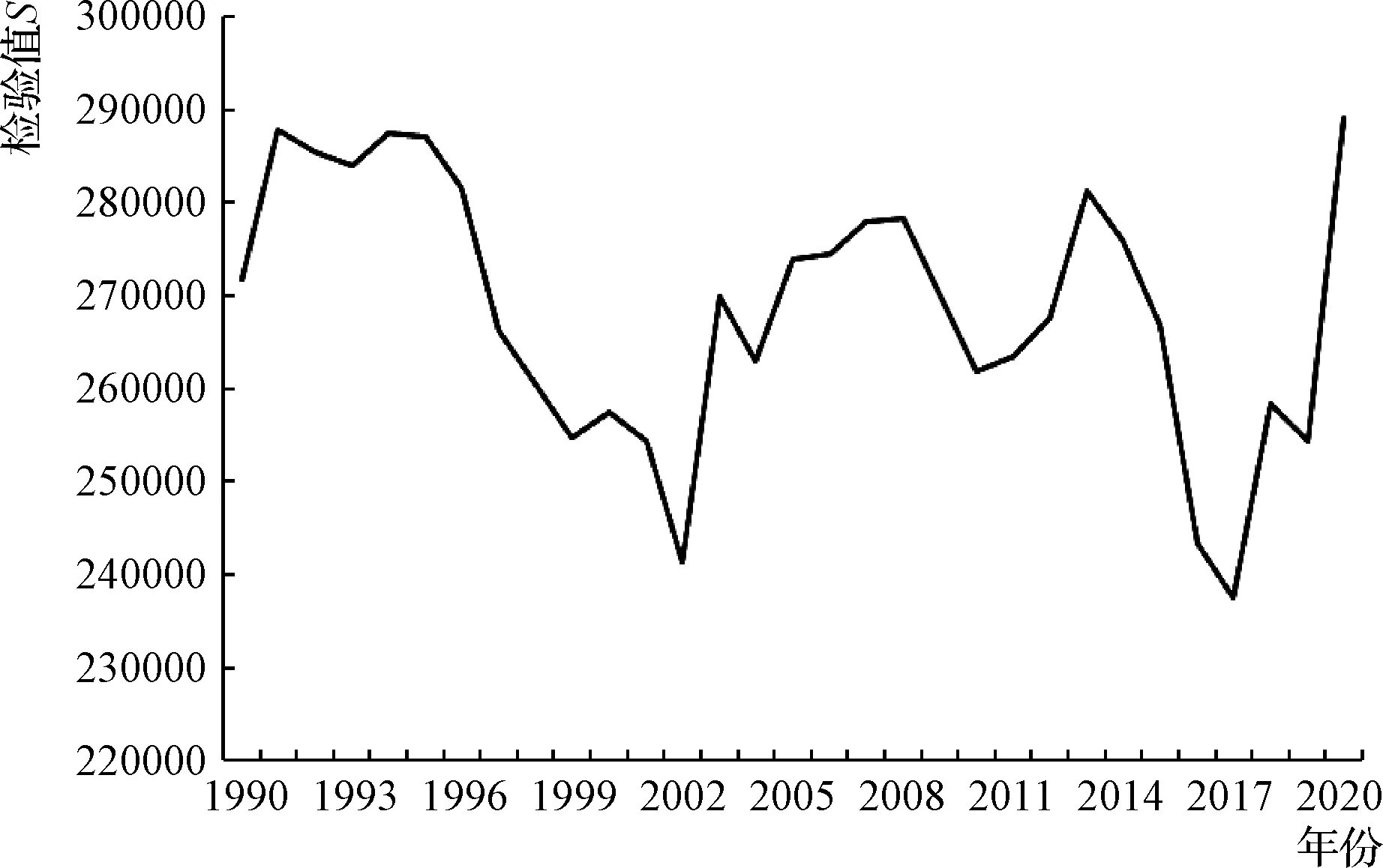
图3 天水测区年降水量有序聚类法检验

图4 天水测区年降水量季-海哈林法检验

2.2 径流

2.2.1 径流趋势变化

对北道水文站1990—2020年年径流数据进行统计分析,得到径流变化序列,见图5。可知渭河上游多年平均年径流量为7.32亿m3,最大年径流量为18.97亿m3(2020年),最小年径流量为1.29亿m3(1997年)。由图5可知,北道水文站年径流量总体呈现升高趋势,线性变化率为0.0952亿m3/a,5年滑动平均显示

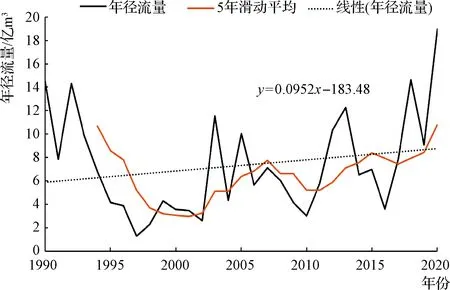
图5 天水测区年径流量年际变化

近31年来年径流量呈现缓慢上升趋势。线性回归法、非参数检验法、肯德尔秩次检验法均一致诊断为“趋势不显著”,但计算检验值与标准值较接近(见表3),说明上升与非上升趋势处于临界状态。

表3 天水测区年径流量序列趋势诊断结果

2.2.2 径流突变点诊断

北道水文站年径流量M-K突变检验结果见图6,设置0.05显著性水平,即得到置信区间临界值为-1.96和1.96,根据分析,得出2013年年径流量UF<0,说明年径流量处于下降趋势,2013—2020年处于上升趋势。20世纪90年代UF、UB值超过置信区间临界值,表明在此期间年径流量变化显著。整体来看,采用有序聚类法和季-海哈林法同步验证,得出检验值|T|=2.42>U(0.05/2)=1.96,根据检验值趋势图可分析出,在2017年资料系列达到最值,根据方法的突变点判别,均在2017年前后均值发生显著跳跃,见图7、图8,与M-K检验结果一致。

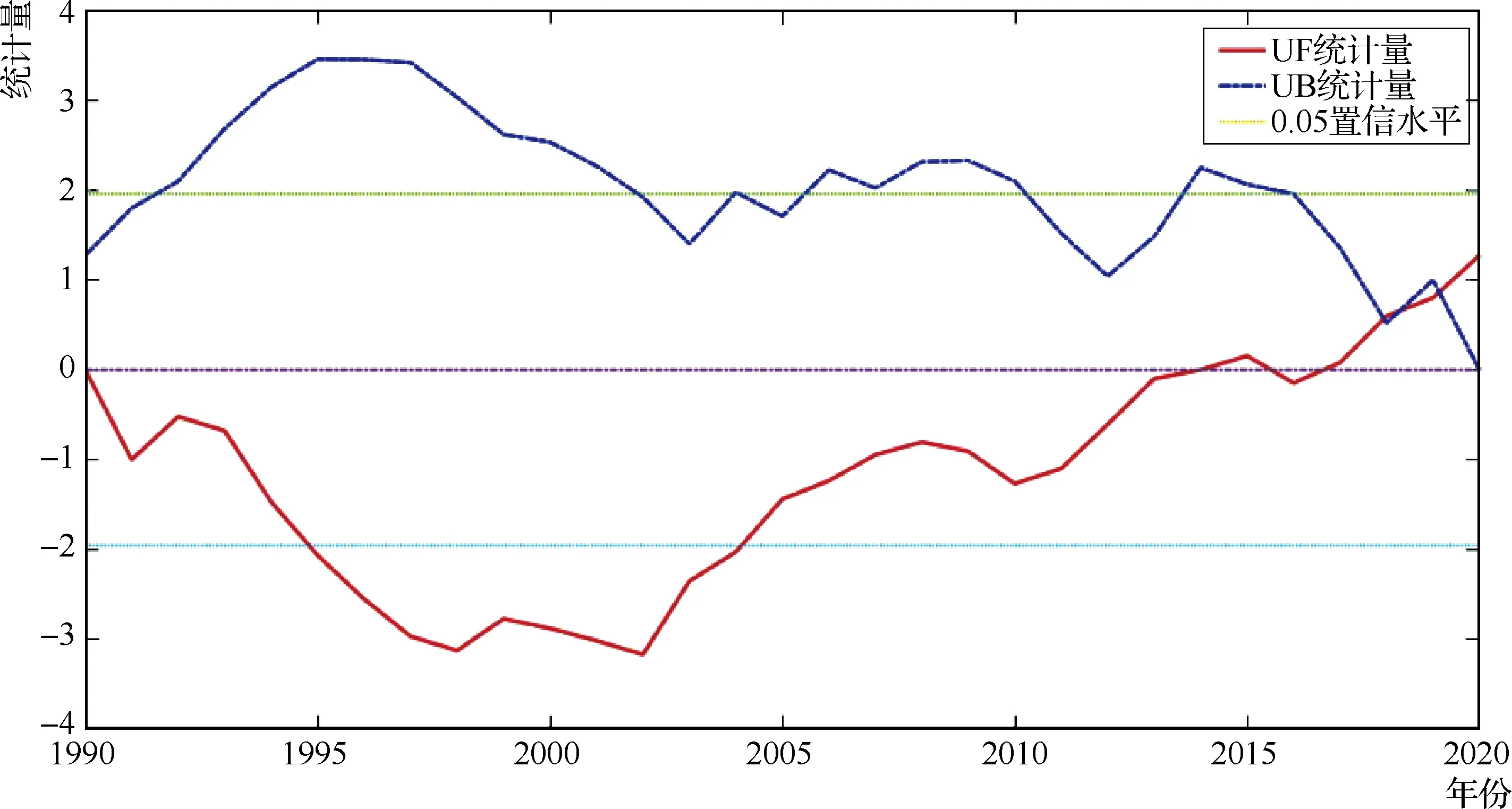
图6 天水测区年径流量M-K秩次检验

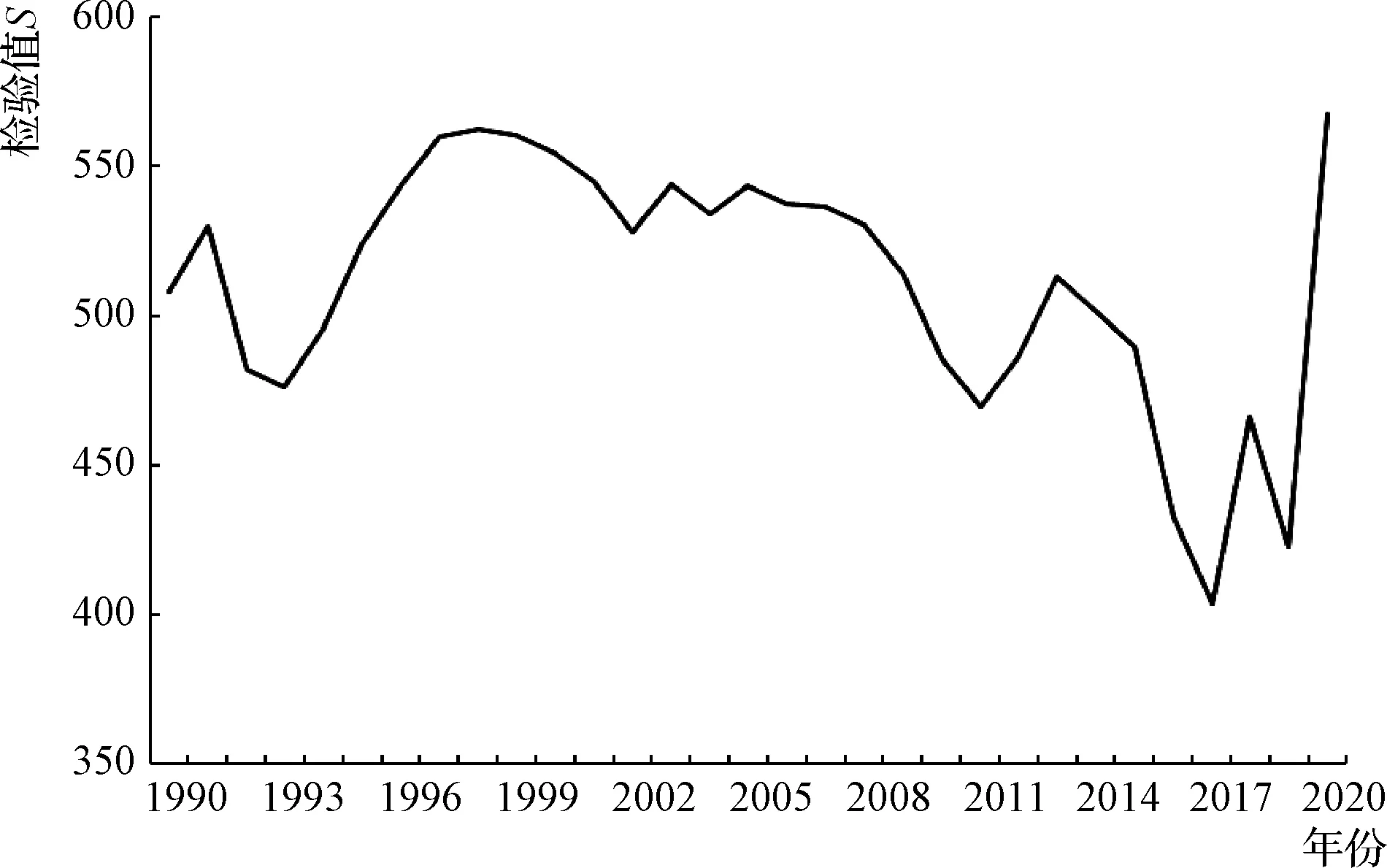
图7 天水测区年径流量有序聚类法检验

图8 天水测区年径流量季-海哈林法检验

根据以上方法,设定置信度为0.95,最小分割尺度为25,根据年径流变异分析结果,天水测区年径流量启发式分割检验见图9。由图9可知,2018年对应的T值最大,并且相对应的P(Tmax)为0.61,小于临界值0.95,说明2018年为第一突变点[5-6]。

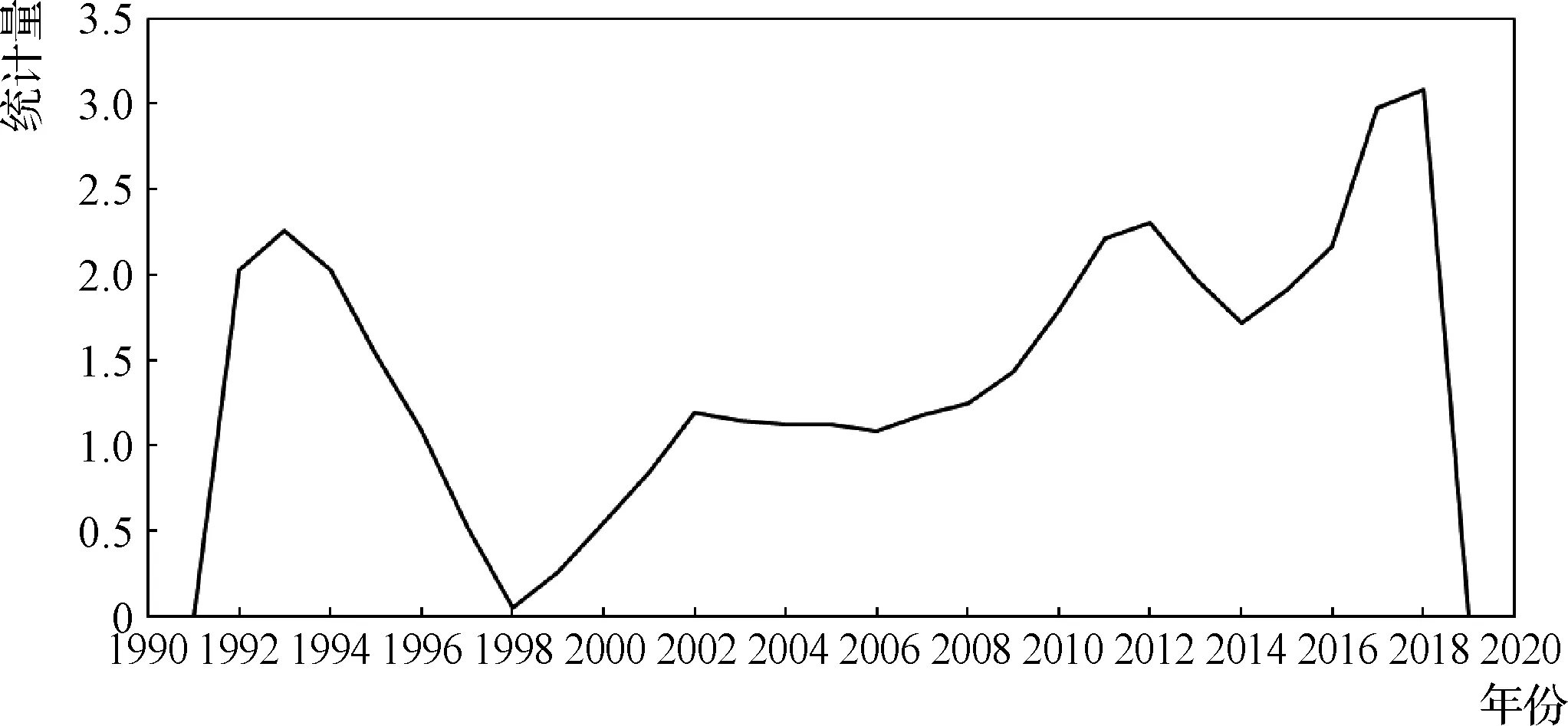
图9 天水测区年径流量启发式分割检验

2.2.3 降水径流EMD结果分析

运用EMD方法对天水测区多年来降水和径流数据进行多尺度分解,结果见图10、图11,其中包含有多个具有物理意义的平稳固有模态函数(Intrinsic Mode Functions,IMF)和具有单一性的趋势项(Re-sidual,Res),从中可得出如下重要结论:

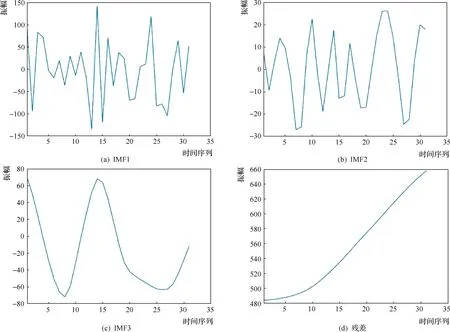
图10 年降水量序列EMD分解

图11 年径流量序列EMD分解

a.根据EMD原理,渭河上游天水测区降水量,原始分量除外,可分解成3个不同波动周期的振荡分量,径流量可分解成4个不同波动周期的振荡分量,反映了该测区降水和径流在不同变化程度上的多时间尺度性。

b.20年代初及2015年前后降水和径流IMF1分量变动幅度大,降水是径流变化的主要影响因素,周期较为一致。IMF1是第一个本征模态函数,波动振幅最大,频率最高,波长最短,周期2～5年,随后的分解过程中,本征模态函数振幅逐渐减小,频率逐渐降低,波长逐渐变大,其对原始时间序列的影响程度逐渐降低。

c.Res分量显示的是天水测区年降水量和年径流量的整体变化趋势,近31年来整体呈急剧上升趋势。EMD通过信号逐步去噪和趋势剔除[7],实现了序列的平稳化处理。

2.3 泥沙变化

2.3.1 输沙量趋势变化

对北道水文站1990—2020年年输沙量数据进行统计分析,得到变化序列,见图12。渭河上游多年平均年输沙量为3490万t,最大年输沙量为15600万t(1992年),最小年输沙量为298万t(2014年)。北道水文站年输沙量总体呈现下降趋势,线性变化率为198万t/a,5年滑动平均显示近31年来输沙量呈现持续下降趋势。采用线性回归法、非参数检验、肯德尔秩次检验方法分析结果一致,均为下降趋势显著,见表4。

图12 天水测区年输沙量年际变化

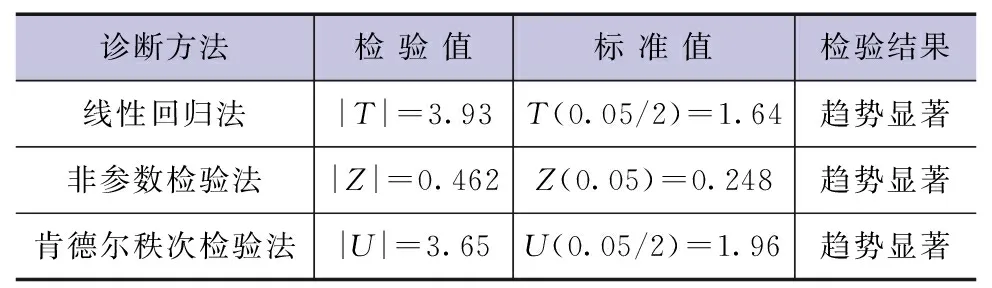
表4 天水测区年输沙量序列趋势诊断结果

2.3.2 泥沙突变点诊断

对北道水文站年输沙量进行M-K突变检验,见图13。设置0.05显著性水平,即得到置信区间临界值为-1.96和1.96。根据分析得出,在1990—2020年,UF<0,说明年输沙量呈显著下降趋势。20世纪90年代以来,UF和UB曲线存在较多交点,整体来看,相关检验值[|U|=3.651]<[U(0.05/2)=1.96],趋势显著。采用有序聚类法和季-海哈林法同步验证,得出检验值[|T|=4.67]>[U(0.05/2)=1.96],根据检验值趋势图分析出,在1992年资料系列达到最值,根据方法的突变点判别,资料系列在1992年前后均值发生显著跳跃,见图14和图15,与M-K检验结果一致。

图13 天水测区年输沙量M-K秩次检验

图14 天水测区年输沙量有序聚类法检验

图15 天水测区年输沙量季-海哈林法检验

2.3.3 径流-泥沙关系分析

通过绘制径流-泥沙双累积曲线(见图16),可以看出累积曲线显著分为3个阶段,1990—1992年为一个变化时段,该时段相关系数为0.9994;1993—2002年为一个变化时段,该时段相关系数为0.9935;2003—2020年为一个变化时段,该时段相关系数为0.9563;每个阶段相关性均较好。由图16可知,1992年、2002年前后均为输沙量的突变点,累积输沙量的趋势线存在变缓趋势,说明在径流增加的情况下,输沙量逐渐减少,这与流域内的生态景观工程和近些年的水沙治理成效都有着密不可分的关系。

图16 径流-泥沙双累积曲线

3 结 语

经过分析,天水测区属干旱半干旱区,径流主要由降水补给,南北两岸支流有不同水文特性,南岸面积小,地形陡峻,地表多为森林覆盖或为剥蚀山地,降水较多,植被好,支流距渭河干流距离短,水多沙少;北岸支流水少沙多,水量较贫,主要为暴雨洪水,陡涨陡落。流域降水、径流分别采用线性回归、非参数检验、肯德尔秩次检验三种方法分析,结果一致,均为趋势性不明显,但统计值与判断值较接近,说明处在临界状态,而采用滑动平均曲线均有微弱上升趋势。分别采用M-K秩次检验、启发式分割、有序聚类法、季-海哈林突变诊断方法进行同步验证,得出降水和径流均在2017年前后产生突变一致性结论。对于年输沙量分别采用线性回归、非参数检验、肯德尔秩次检验三种方法分析,结果一致,均为下降趋势明显。采用启发式分割、有序聚类、季-海哈林突变诊断方法得出,在1992年前后产生突变的一致结论,采用径流-泥沙双累积曲线法分析,明显发现年输沙量存在1992年和2002年两个突变点。

天水测区在降水、径流无明显减少的情况下,年输沙量减少趋势明显,说明流域内土地利用、生态保护、植被恢复等人类活动剧烈,特别是水土保持工作成效显著。

采用径流-泥沙双累积曲线法发现年输沙量存在两个突变点,但基于数理统计分析判断的启发式分割、有序聚类、季-海哈林突变诊断方法年输沙量诊断为一个,可见数理统计分析判断方法对于多个突变点的诊断有待进一步完善。