联合作答精度和作答时间的概率态认知诊断模型*

田亚淑 詹沛达 王立君

联合作答精度和作答时间的概率态认知诊断模型*

田亚淑 詹沛达 王立君

(浙江师范大学心理学院; 浙江省儿童青少年心理健康与心理危机干预智能实验室; 浙江省智能教育技术与应用重点实验室, 金华 321004)

对多模态数据的联合分析是改进结果评价、健全综合评价的主要途径。针对概率态认知诊断模型(CDM)仅能分析题目作答精度(RA)的局限, 本文基于联合−层级建模框架和联合−交叉负载建模框架提出三个可联合分析RA和题目作答时间(RT)的概率态联合CDM。模拟研究和实证研究结果表明：(1)新模型参数估计返真性良好, 额外引入RT有助于提高参数估计精度并提供有关个体加工速度的测量; (2)基于联合−交叉负载建模框架构建的模型对测验情境的兼容性优于基于联合−层级建模框架构建的模型; (3)概率态属性比确定态属性更精细地反映个体对属性的掌握情况。

认知诊断, 概率态属性, 题目作答时间, 联合建模框架, 交叉负载

1 引言

认知诊断测评可以提供有关学生知识结构或加工技能(统称为“(潜在)属性”)的诊断信息; 可为教师实施补救教学或有针对性干预提供参考, 有助于促进学生发展(Tang & Zhan, 2021)。认知诊断模型(cognitive diagnosis model, CDM)是刻画属性与外显行为之间关系的统计模型, 其建构的合理性(如, 模型与测试情境的匹配度)影响诊断结果的准确性和可解释性。目前, 大致可将属性分为两种：确定态属性(deterministic attribute)和概率态属性(probabilistic attribute)：前者将被试的属性掌握状态诊断为确定的类别(如, “1”表示掌握, “0”表示未掌握); 而后者将被试对属性的掌握诊断为0到1的连续状态, 用于量化被试对属性的掌握概率(如, “0.8”表示掌握概率为80%) (Zhan, Wang, et al., 2018)。Zhan (2021)进一步指出概率态属性是“个体掌握某种属性的说法是正确的概率(the probability that the statement that a person masters an attribute is true)”, 即概率态属性并没有否定属性的二分特性, 只是从概率视角对其进行解读和建模。相比于确定态属性, 概率态属性能更精细地区分被试间的个体差异(詹沛达, 田亚淑等, 2020); 尤其是在描述被试发展情况时, 基于概率态属性的反馈比基于确定态属性的反馈更精细地反映学生的发展变化(Zhan, 2021), 更有益于肯定学生的努力。

针对不同的测验情境和理论假设, 研究者们提出了不同的概率态CDM (毛秀珍, 2014; 詹沛达, 边玉芳, 2015; Liu et al., 2018; Zhan, Wang, et al., 2018; Zhan, 2021)。然而, 现有的概率态CDM仅能分析单一模态数据——题目作答精度(response accuracy, RA), 忽略了诸如题目作答时间(response times, RTs)、鼠标点击次数和行动序列等过程数据。其中, RT作为一种有代表性的过程数据, 是指被试作答每道题目花费的时间; 可以反映被试的(潜在)加工速度。目前, 无论是大规模测评项目[如, 国际学生评估项目(PISA)、美国国家教育进展评估(NAEP)和国际数学与科学趋势研究(TIMSS)], 还是一些具有实验性质的小规模测评(如, 游戏化测评), 记录RT已经成为一种常态。

近些年, 研究者们开发了一系列RT分析模型(郭磊等, 2017; de Boeck & Jeon, 2019)。已有研究表明数据分析时额外引入RT, 有助于提高被试参数估计的精度(Bolsinova & Tijmstra, 2018; Zhan, Jiao, & Liao, 2018), 并有助于识别被试的异常作答行为(Wang & Xu, 2015); 通过RT所反映的加工速度还可以进一步探索被试的认知风格(如, Yan, 2010), 丰富诊断反馈所包含的信息(Zhan et al., 2022)。鉴于在数据分析中引入RT的诸多优势, 如何将RT引入概率态CDM以进一步提高参数估计精度并丰富诊断反馈信息, 是一个有待解决的方法学问题。

目前, 在认知诊断测评中, 联合−层级认知诊断建模框架(Zhan, Jiao, & Liao, 2018)是同时分析RA和RT的主要框架之一, 如图1所示。在该框架中, RA用于测量被试的属性和(潜在)能力、RT用于测量被试的加工速度。该框架具有较高灵活性, 可通过替换该框架中的测量模型实现不同的数据分析需求(Huang, 2020; Peng et al., 2022; Zhan et al., 2022; 詹沛达, 2022; 郑天鹏等, 2023)。目前, 该框架下的所有模型都是针对确定态属性构建的, 难以精细化区分被试间的个体差异或提供精细化反馈。鉴于该框架的灵活性, 可尝试将概率态CDM引入该框架, 构建可联合分析RA和RT的联合−层级概率态CDM, 这是本研究拟解决的第一个主要问题。

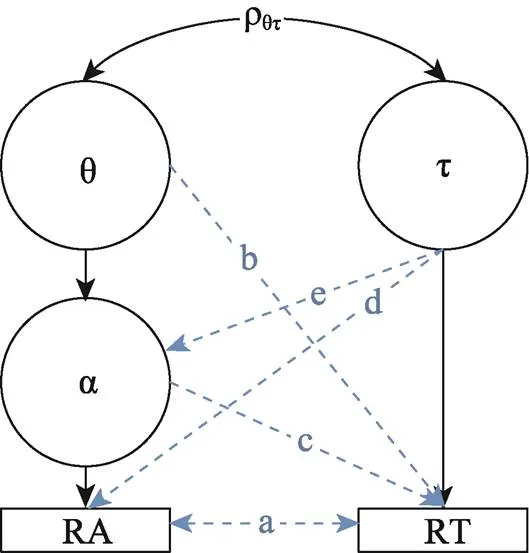
图1 联合−层级认知诊断建模框架中条件独立性假设示意图

注：RA = 作答精度; RT = 作答时间; θ = 能力; τ = 加工速度; α = 属性; ρ = 能力与加工速度的相关系数; 虚线表示模型的条件独立假设: a = 给定能力和加工速度后, RT和RA条件独立; b = 给定加工速度后, 能力和RT条件独立; c = 给定能力和加工速度后, 属性和RT条件独立; d = 给定能力后, 加工速度和RA条件独立; e = 给定能力后, 加工速度和属性条件独立。

联合−层级认知诊断建模框架作为联合−层级建模框架(van der Linden, 2007)在认知诊断测评中的应用, 尽管得到了较广泛的研究支持, 但基于该框架所构建的联合模型至少需要满足5个条件独立性假设才能够合理、准确地对数据进行分析和解释。如图1所示：

(1)给定能力和加工速度后, RT和RA之间条件独立(图1中a);

(2)给定加工速度后, 能力和RT之间条件独立(图1中b);

(3)给定能力后和加工速度后, 属性和RT之间条件独立(图1中c);

(4)给定能力后, 加工速度和RA之间条件独立(图1中d);

(5)给定能力后, 加工速度和属性之间条件独立(图1中e)。

然而, 有研究发现实际测验中存在违背上述假设的情况。比如, Meng等人(2015)发现RT和RA之间存在一个变量(如, 题目难度)使得两者有相依性; Bolsinova等人(2017)尝试对RA和RT之间的条件独立性进行建模; Bolsinova和Tijmstra (2018)释放能力和RT之间条件独立性假设后发现可以进一步提高能力的估计精度。同时, 上述条件独立性假设也使得联合−层级认知诊断建模框架只能通过能力和加工速度之间的相关性(即, 图1中ρ)来获取RT中所包含的辅助信息, 进而达到提高诊断分类准确性的目的(詹沛达, 2022); 类似的理论缺陷在联合−层级建模框架中也存在(Ranger, 2013; Bolsinova & Tijmstra, 2018)。而在实际测验中, 可能存在能力和加工速度之间的相关系数较低, 甚至趋近于零的情况(Bolsinova et al., 2017); 此时基于联合−层级认知诊断建模框架所构建的模型将难以从RT中获取能力或属性的相关信息。针对上述局限, 詹沛达(2022)提出了联合−交叉负载(载荷)认知诊断建模框架, 该建模框架通过交叉负载直接利用RT为能力或属性提供信息, 释放了联合−层级认知诊断建模框架的部分条件独立性假设(图1中b或c), 增加了建模框架的适用范围。郑天鹏等人(2023)在联合−层级认知诊断建模框架的基础上尝试释放了图1中条件独立性d, 认为被试的加工速度会影响其正确作答概率。虽然释放图1中任一条件独立性假设路径在理论上都是可以的, 但考虑到联合建模的主要目的之一是为了促进对核心特质(即能力)的估计精度, 所以释放b或c路径是一种更常见的选择(Bolsinova & Tijmstra, 2018; 詹沛达, 2022)。基于此,本研究拟在所构建的联合−层级概率态CDM的基础上, 借鉴联合−交叉负载认知诊断建模框架, 进一步构建联合−交叉负载概率态CDM (joint-cross- loading CDM for probabilistic attributes), 这是本研究拟解决的第二个主要问题。

针对上述两个研究问题, 本研究旨在丰富概率态CDM的可分析数据类型, 并为以精细化诊断作为数据分析目标的测评提供框架支持。在实践中, 全面且精准地了解学生的学习现状是因材施教的必要前提; 使用联合概率态CDM不仅可以实现对学生学习状态的精细化区分, 为因材施教和精准教学落地提供数据支持, 还可以提供有关学生加工速度的分析结果, 有助于了解学生的认知或学习风格。

下文首先简单回顾联合−层级和联合−交叉负载认知诊断建模框架, 以及一个有代表性的概率态CDM——高阶概率态输入, 噪音连接(higher-order probabilistic-inputs, noisy conjunctive, HO-PINC)模型(Zhan, Wang, et al., 2018)。其次, 依次通过两个模拟研究分别阐述并探究基于上述两框架所构建的三个新模型。然后, 通过第三个模拟研究来交叉对比三个新模型的表现。再然后, 以一则PISA 2012计算机化数学测验数据为例来展现三个新模型的实践可应用性及相对优势。最后, 总结研究并指出研究局限及未来的拓展方向。

2 两个联合认知诊断建模框架与概率态认知诊断模型

图2呈现了两种联合认知诊断建模框架的示意图, 其中图2(a)为联合−层级认知诊断建模框架(Zhan, Jiao, & Liao, 2018)。该建模框架包含两层模型：第一层为测量模型, 比如以高阶DINA(de la Torre & Douglas, 2004)作为RA的测量模型, 并以对数正态RT模型(lognormal RT model, LRTM) (van der Linden, 2006)作为RT的测量模型; 第二层为结构模型, 采用二元正态分布描述能力与加工速度之间的关系。图2(b)和图2(c)为联合−交叉负载认知诊断建模框架下的两种建模方式(詹沛达, 2022)：前者基于能力, 假设RT先对能力提供辅助信息(即被试的能力高低会影响RT), 进而间接影响属性的分类准确性; 后者基于属性, 假设RT直接对属性提供辅助信息(即被试的属性掌握情况会影响RT)。

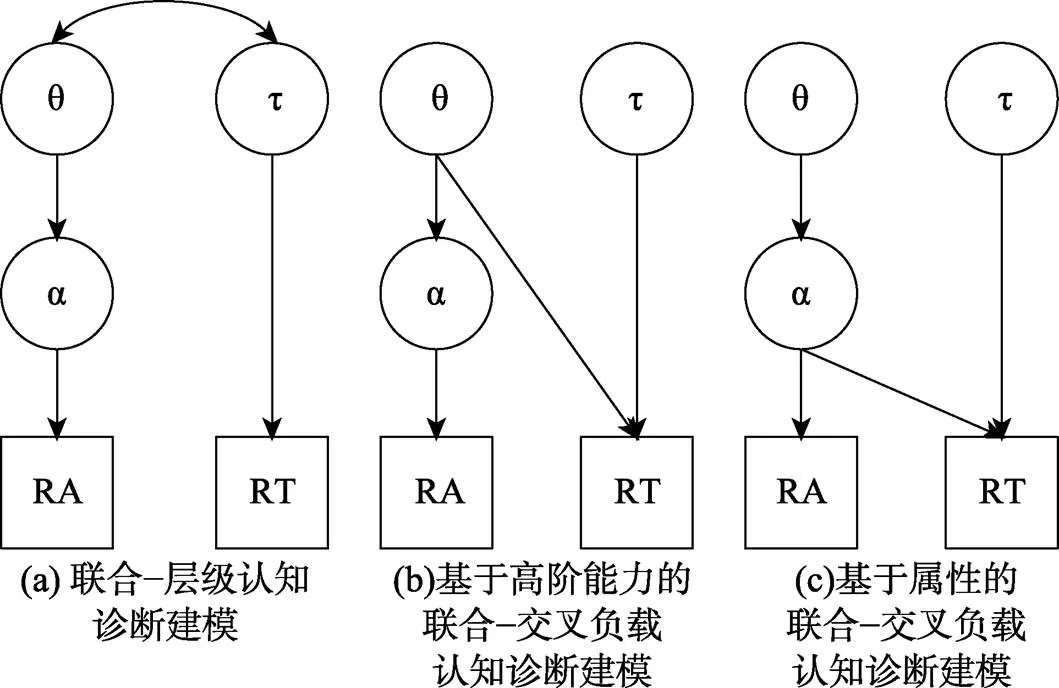
图2 联合−层级和联合−交叉负载认知诊断建模示意图

注：RA = 作答精度; RT = 作答时间; θ = 能力; τ = 加工速度; α = 属性。

目前两建模框架中属性均为确定态属性(即二分属性), 进而能力与属性之间的关系被定义为(de la Torre & Douglas, 2004)：

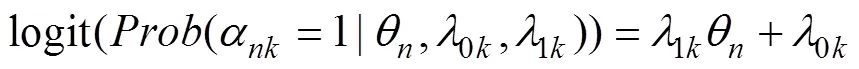
与确定态属性不同, 概率态属性常被赋值为一个0到1之间的(概率)数值。考虑到属性之间的相关性, Zhan, Wang等(2018)将概率态属性构建为：

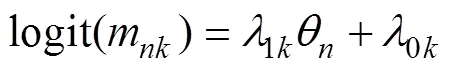
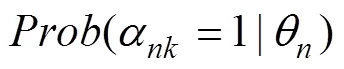
基于公式2, HO-PINC的题目作答函数(item response function, IRF)可以被构建为：

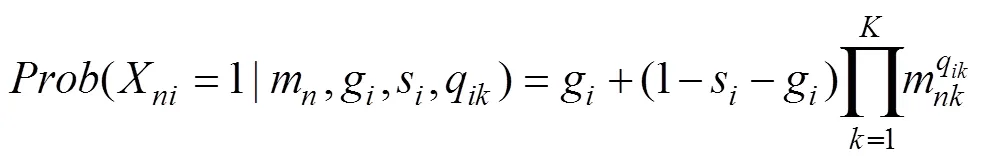
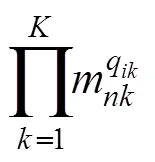
3 研究1：针对作答精度和时间的联合−层级概率态认知诊断模型

3.1 模型构建

遵循联合−层级认知诊断建模框架, 新模型共包含两层模型。第一层为测量模型, 其中RA模型采用HO-PINC (公式3), RT模型采用LRTM：

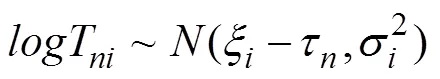
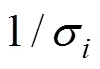
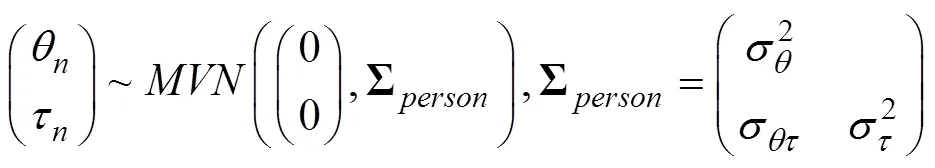
和

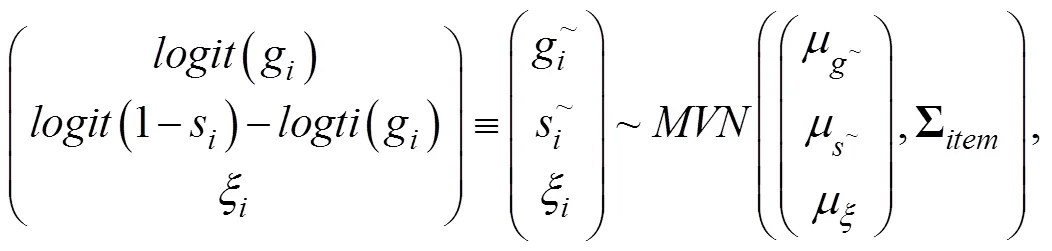
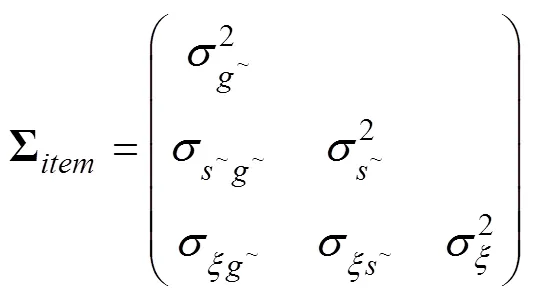
基于联合−层级建模框架, 为使模型可识别, JRT-PINC需要满足如下条件独立性假设：

(1) 给定θ后, 各m满足条件独立;

(2) 给定m后, 各X满足条件独立;

(3) 给定τ后, 各logT满足条件独立;

(4) 给定θ和τ后,X和logT满足条件独立;

(5) 给定θ后, 各τ和m满足条件独立;

(6) 给定θ和m, 各τ和X满足条件独立;

(7) 给定θ和τ后,m和logT满足条件独立;

(8) 给定τ后, θ和logT满足条件独立。

其中, 前3个条件独立性假设是测量模型自身所需的, 后5个条件独立性假设是联合−层级建模框架所需的(同引言)。

3.2 参数估计

本研究采用全贝叶斯MCMC算法对JRT-PINC进行参数估计, 使用R软件中的R2jags包(Version 0.7-1)调取JAGS软件(Version 4.3.0)实现参数估计。网络版附录S1节对比了新模型在有经验信息先验下和低信息先验下的表现, 两种情况下结果一致性较高, 表明新模型对包含不同信息量的先验分布具有一定的鲁棒性。新模型的参数估计JAGS代码及示例数据见https://osf.io/hys7c/?view_only=cb357a6f5032424ab36b7fbda6df4d40, 关于如何使用JAGS进行贝叶斯参数估计可参见Zhan等(2019)。

3.3 模拟研究

3.3.1 数据生成

模拟研究包括4个自变量：(1)样本量()：200和500; (2)题目数量()：15和30; (3)能力与加工速度的相关系数(ρθτ)：−0.5, −0.3, 0, 0.3和0.5; (4)数据分析模型：JRT-PINC和HO-PINC, 用于探究额外引入RT对参数估计精度带来的影响。此外属性数()固定为5个, 对应的Q矩阵见图3。该Q矩阵包含两个可达矩阵, 以保证其完备性和可识别性(Xu & Zhang, 2016)。研究选择的题目数量、样本量和其他相关参数均参考已有研究设置(如: 詹沛达, 2022)。

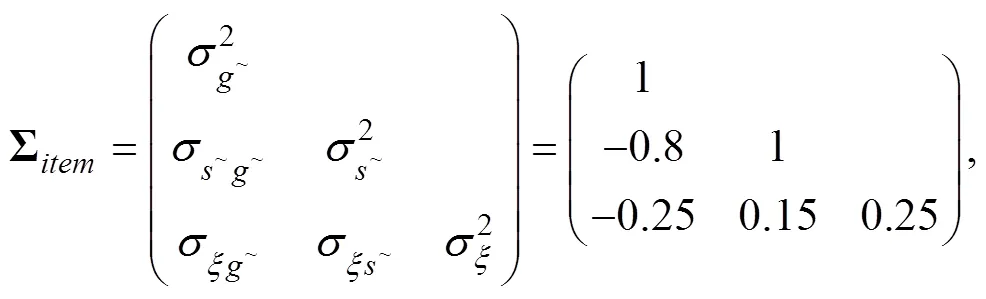
注: 灰色为“1”、白色为“0”；标记*的题目为I = 15

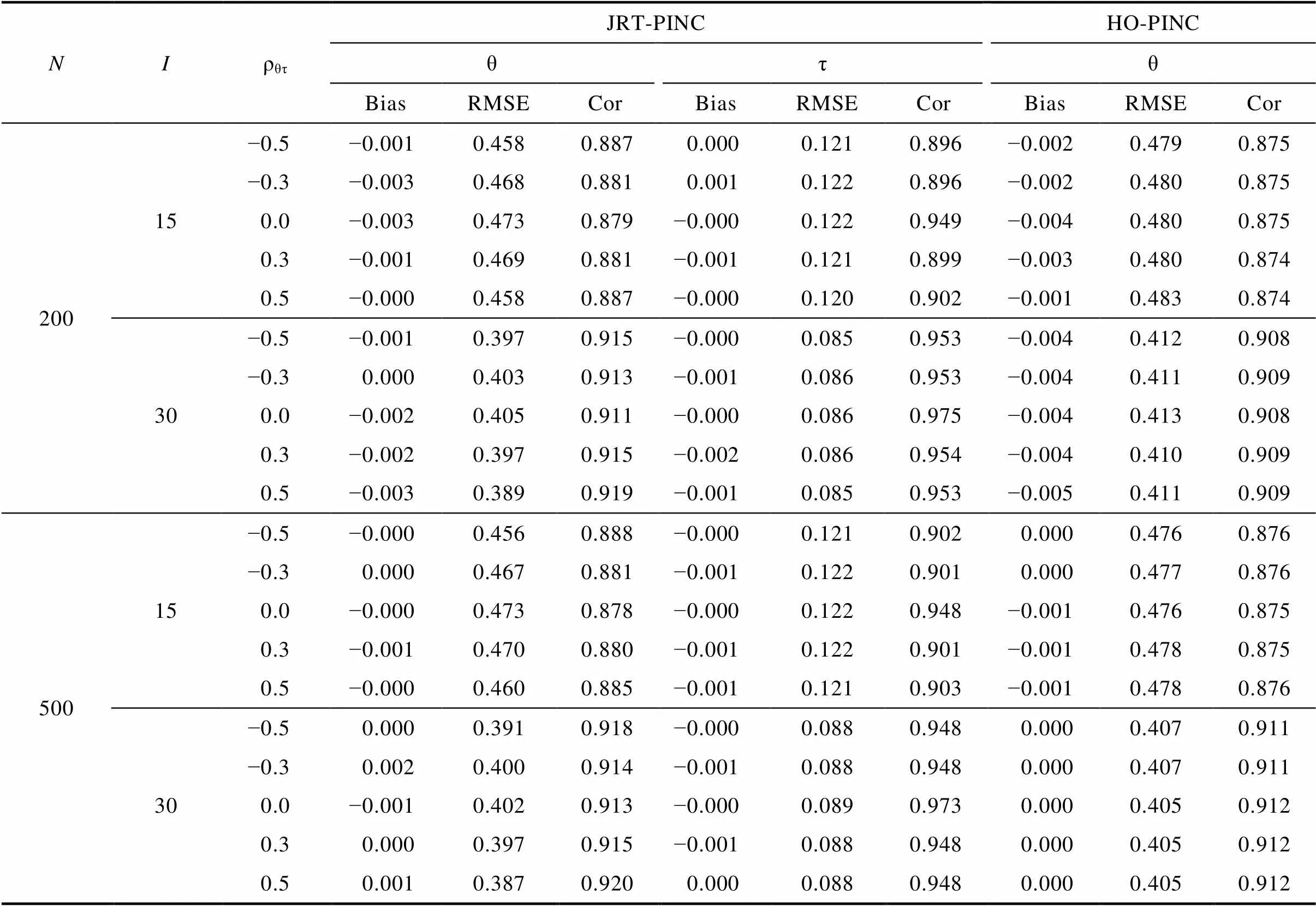
表1 研究1中能力和加工速度参数估计返真性

注: JRT-PINC = 联合−层级概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; θ = 能力; τ = 加工速度; N = 样本量; I = 题目数量; ρθτ= 能力与加工速度的相关系数; Bias = 所有被试的平均偏差; RMSE = 所有被试的平均均方根误差; Cor = 估计值与真值之间的相关系数。

另外, 设定所有题目的时间精度参数均为1/σ= 2。

被试参数依据公式5生成, 其中, 能力的方差σθ2= 1且加工速度的方差σ2= 0.15。被试的概率态属性依据公式2生成, 设定所有属性的区分度参数为λ1k= 1.5, 属性截距参数为λ0= (−1.0, −0.5, 0.0, 0.5, 1.0)’, 此时各属性间为中等相关。最终, 根据JRT-PINC生成所有被试在所有题目上的RA和RT。为减少随机误差, 每种模拟条件下各生成30组数据。

3.3.2 分析

分别使用JRT-PINC和HO-PINC分析该数据。分析采用两条马尔可夫链(初始值随机), 每条链包含10,000次迭代, 前5,000次用于预热(burn-in)。采用潜在量尺缩减因子(potential scale reduction factor, PSRF)检验各参数是否收敛, PSRF < 1.1或1.2表示参数已收敛(de la Torre & Douglas, 2004; Zhan, Jiao, & Liao, 2018)。使用后验均值作为贝叶斯参数估计的“点”估计结果。使用偏差(bias)、均方根误差(root mean square error, RMSE)和皮尔逊积差相关系数(Cor)作为参数估计返真性指标。

3.3.3 结果

结果显示所有参数的PSRF均小于1.2, 表示各参数均已收敛。表1呈现了能力参数和加工速度参数的返真性。首先, JRT-PINC中能力参数(θ)的估计返真性优于HO-PINC的, 表明额外引入RT所包含信息有助于提高能力参数的估计精度。其次, JRT-PINC的能力参数和加工速度参数(τ)在所有模拟条件下的返真性均表现较好, 且Cor指标反映出加工速度参数的返真性优于能力参数的。1由于能力参数和加工速度参数的真值的方差不同(即量尺不同),难以直接通过Bias和RMSE比较两者的返真性优劣; 而Cor指标是从参数估计值和真值的排序一致性角度反映参数估计返真性的, 并不受量尺差异的影响。再有, 对JRT-PINC而言, 能力与加工速度的相关系数(ρθτ)越高, 能力参数的返真性越好, 但加工速度参数的返真性不受影响; 该结果与已有联合模型研究的发现一致, 即两特质之间的相关系数越高, 越有助于能力参数汲取RT中包含的信息。且即便是在ρθτ= 0的条件下, JRT-PINC中能力参数的返真性仍略优于HO-PINC中的; 这可能由于参数估计时JRT-PINC仍假设能力会通过潜在结构(二元正态分布)去利用RT所包含的信息, 进而自由估计两者之间的协方差导致的。此外, ρθτ的正负号对结果没有影响。整体而言, 题目数量越多, 能力与加工速度相关系数越高, JRT-PINC的被试参数返真性越好; 样本量提高也有助于提高被试参数的返真性, 但影响较小; 这意味着200被试的样本量足以满足JRT-PINC被试参数估计的要求。

表2呈现了属性参数的返真性(bias见网络版附录中表S2.1)。首先, JRT-PINC在各条件下的返真性均较好。题目数量越多, 能力与加工速度相关系数越高, 则属性的返真性越好; 同样, 样本量提高也有助于提高属性的返真性, 但影响较小。其次, 各条件下JRT-PINC的返真性均优于HO-PINC的; 同样, 即便是在ρθτ= 0的条件下, JRT-PINC中属性的返真性也略优于HO-PINC中属性的返真性。另外, 不同属性的返真性与属性截距参数有关, 但影响不大, 基本趋势是：属性截距参数越低(即掌握属性难度越大), 则返真性越好。

题目参数和方差协方差矩阵参数估计返真性见网络版附录S2。整体而言, JRT-PINC的题目参数返真性优于HO-PINC的; JRT-PINC中各题目参数在各模拟条件下的返真性均表现较好, 且具有较一致的变化趋势：样本量和题目数量越大, 题目参数的返真性越好, 而能力与加工速度的相关系数影响较小。

4 研究2：针对作答精度和时间的联合−交叉负载概率态认知诊断模型

基于图2(b)和2(c), 研究2通过两个子研究分别构建基于能力的联合−交叉负载PINC (CJRT- PINC-θ)模型(子研究1)和基于属性的联合−交叉负载PINC (CJRT-PINC-)模型(子研究2)。

表2 研究1中概率态属性参数估计的返真性

注: JRT-PINC = 联合−层级概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; θ = 能力; τ = 加工速度; N = 样本量; I = 题目数量; ρ = 能力与加工速度的相关系数。

4.1 子研究1：CJRT-PINC-θ

4.1.1 模型构建

基于图2(b), CJRT-PINC-θ假设被试的能力变化会影响其作答该题目的耗时, 即释放了JRT- PINC中能力和RT之间的条件独立性假设(图1中b)。CJRT-PINC-θ同样包含两层模型, 其中RA的测量模型为HO-PINC模型(公式3), RT的测量模型为：

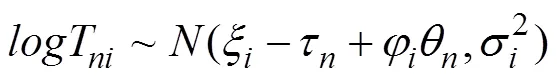
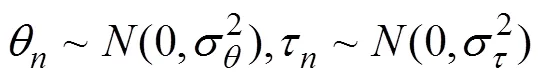
另外, 题目参数之间关系被描述为：

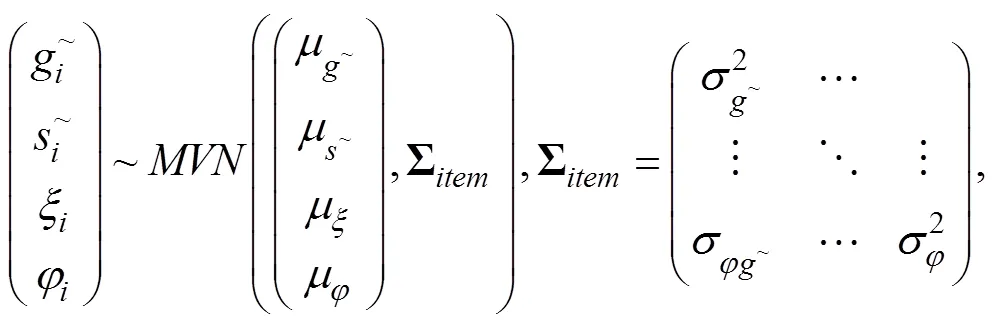
式中各参数含义同上。仍采用贝叶斯MCMC算法对CJRT-PINC-θ进行参数估计, 各待估计参数的先验分布见网络版附录S1。

4.1.2 模拟研究：数据生成与结果

为了更符合实际测试的复杂情境, 模拟研究设置不同题目中θ对RT的影响不同(詹沛达, 2022)：设定自变量交叉负载(φ)满足方差为0.15的正态分布, 其中低影响效应μφ= 0.1, 高影响效应μφ= 0.5。固定样本量= 200, 题目数量= 15, 其余参数设定与研究1相同。根据CJRT-PINC-θ (公式2～3和公式7～9)生成所有被试在所有题目上的RA和RT。

使用CJRT-PINC-θ和HO-PINC分析该数据。结果显示所有参数的PSRF均小于1.2, 表示各参数均已收敛。表3呈现了能力参数和加工速度参数的估计返真性。首先, CJRT-PINC-θ的返真性均优于HO- PINC的, 表明额外引入RT所包含信息有助于提高参数估计精度。其次, 随着交叉负载均值提高, 能力参数的返真性有所提高但加工速度参数的返真性有所下降, 这与詹沛达(2022)的发现一致。表4呈现了属性参数估计返真性。首先, CJRT-PINC-θ在不同模拟条件下属性参数的返真性均较好, 且均优于HO-PINC的。题目参数和方差协方差矩阵参数的返真性见网络版附录表S3.1和表S3.2。整体而言, 不同模拟条件下CJRT-PINC-θ的参数返真性均较好, 且优于不考虑RT的HO-PINC的。

表3 研究2(子研究1)中被试参数估计返真性

注: CJRT-PINC-θ = 基于能力的联合−交叉负载概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; θ = 能力; τ = 加工速度; μφ= 交叉负载均值; Bias = 所有被试的平均偏差; RMSE = 所有被试的平均均方根误差; Cor = 估计值与真值之间的相关系数。

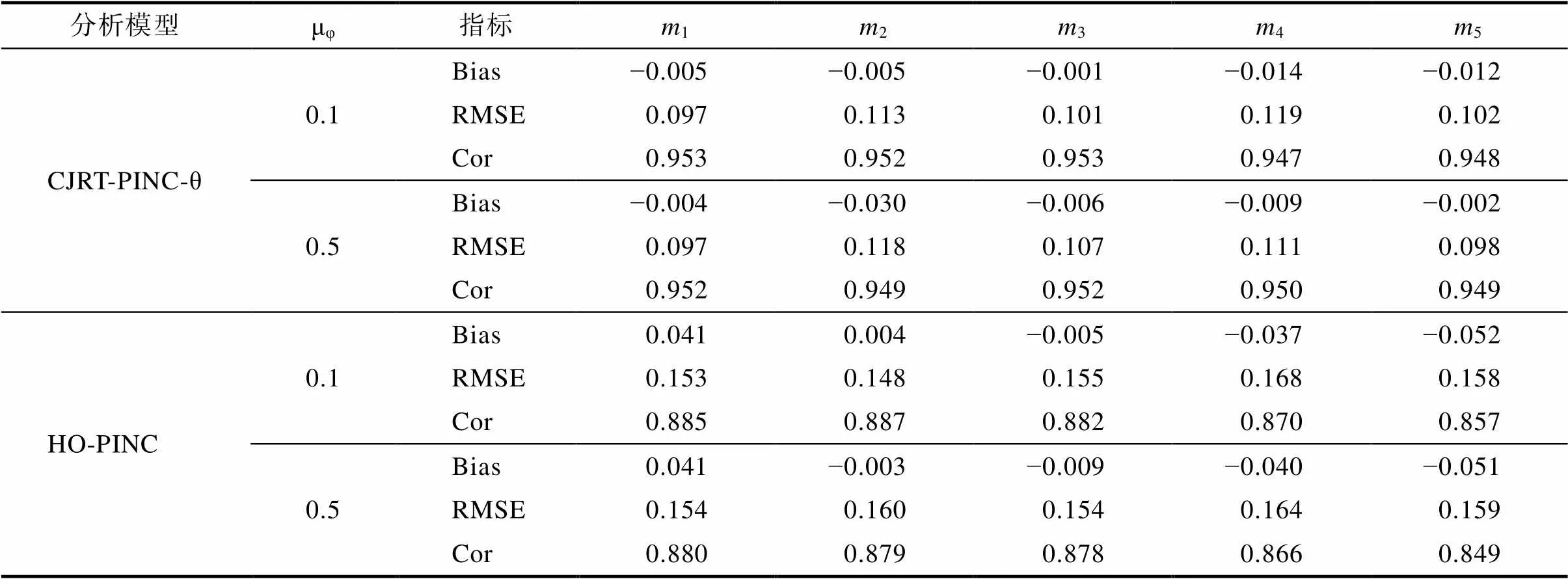
表4 研究2(子研究1)概率态属性参数估计返真性

注: CJRT-PINC-θ = 基于能力的联合−交叉负载概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; μφ= 交叉负载均值;= 概率态属性; Bias = 所有被试的平均偏差; RMSE = 所有被试的平均均方根误差; Cor = 估计值与真值之间的相关系数。

4.2 子研究2：CJRT-PINC-m

4.2.1 模型建构

基于图2(c), CJRT-PINC-假设被试对属性的掌握情况会影响其完成该题目的耗时, 被试对题目所考查的所有属性的掌握概率越高则对RT的影响越大, 即该模型释放了JRT-PINC中属性和RT之间的条件独立性假设(图1中c)。CJRT-PINC-同样包含两层模型, 其中RA的测量模型为HO-PINC模型(公式3), RT的测量模型为：

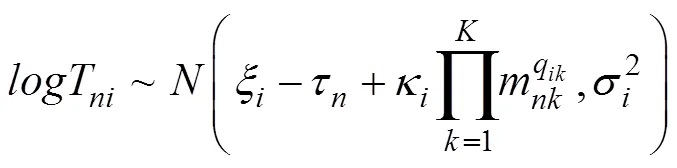
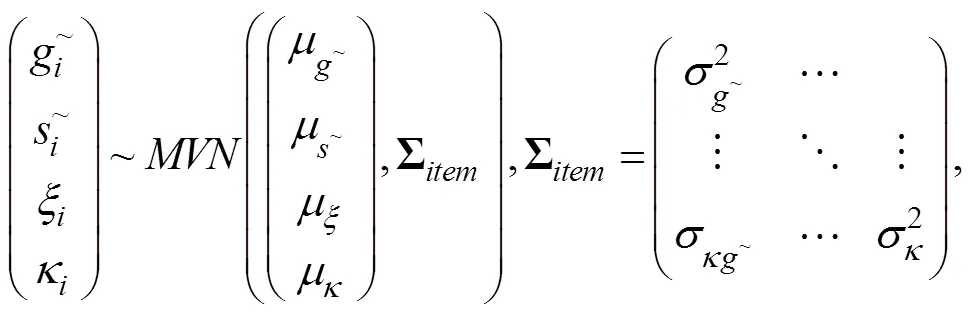
式中各参数含义同上。仍采用贝叶斯MCMC算法对CJRT-PINC-进行参数估计, 各待估计参数的先验分布见网络版附录S1。

4.2.2 模拟研究：数据生成与结果

该部分具体内容见网络版附录S3.2。整体而言, CJRT-PINC-在不同模拟条件下模型参数的返真性良好, 均优于不考虑RT的HO-PINC的。

5 研究3：新模型之间的交叉比较

5.1 数据生成与分析

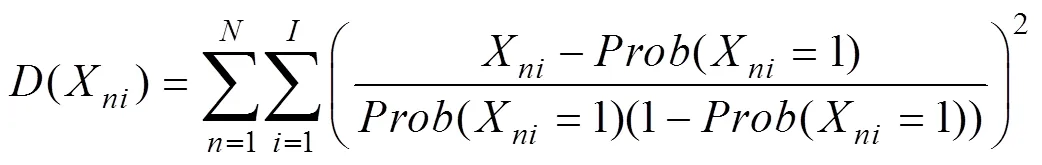
5.2 结果

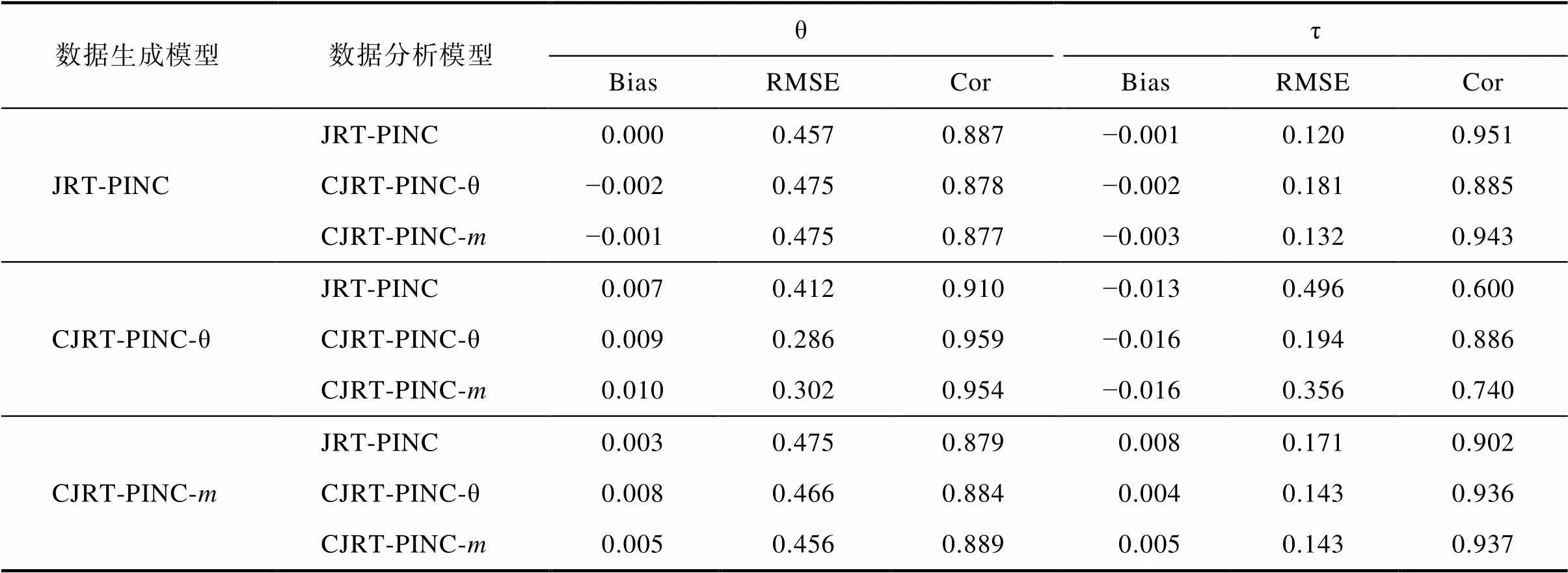
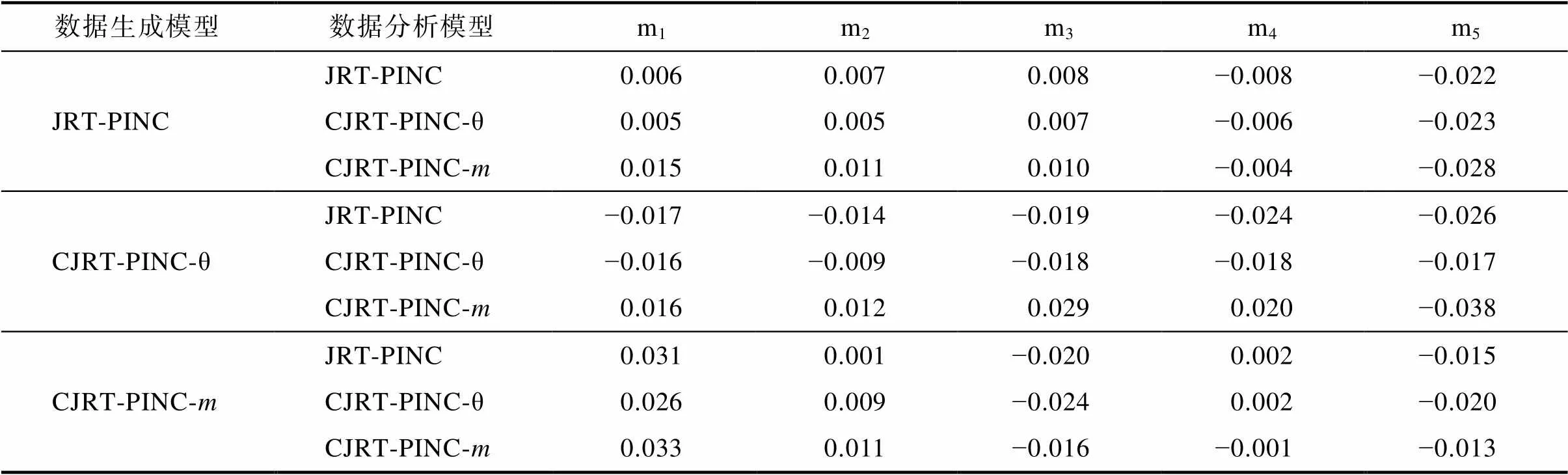
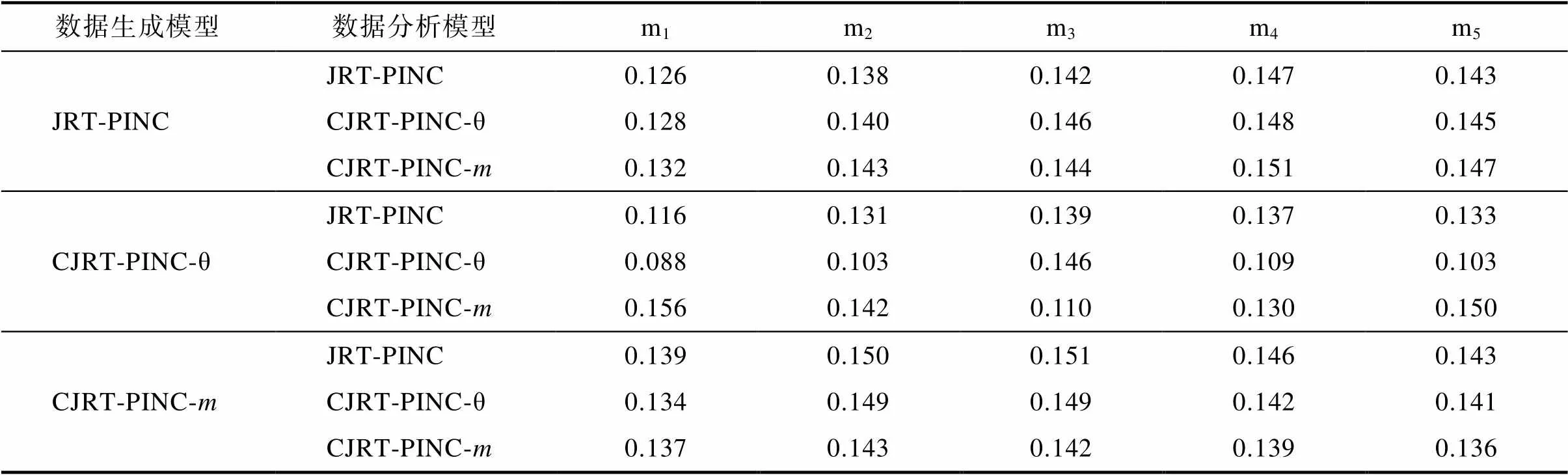
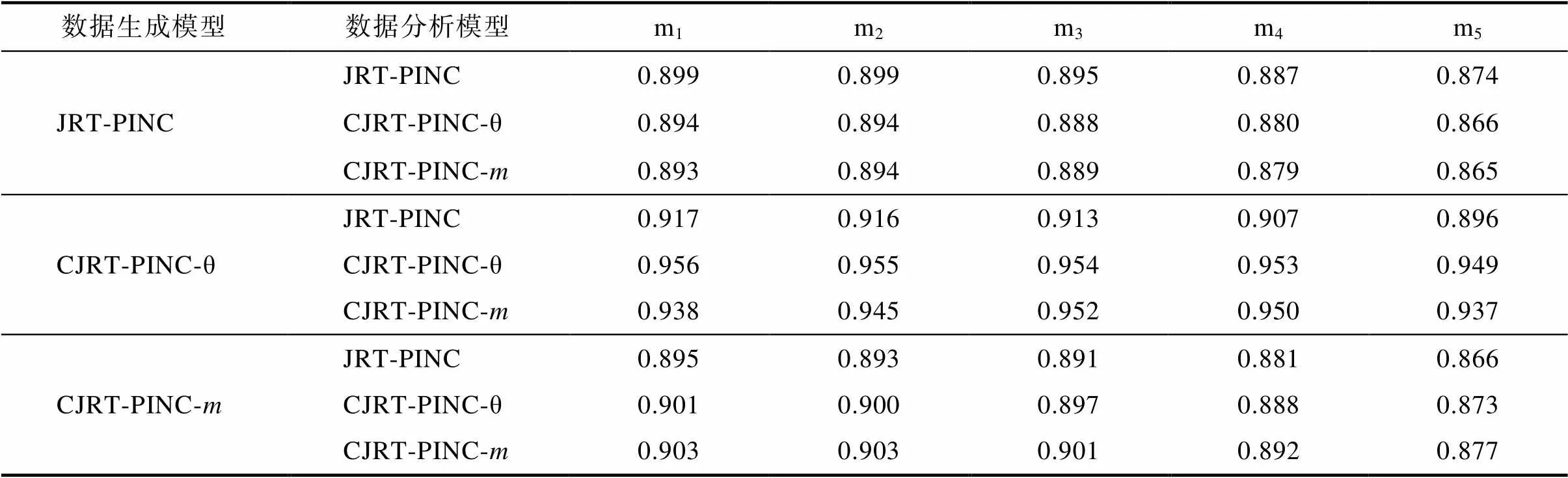
结果显示所有参数的PSRF均小于1.2, 表示各参数均已收敛。表5呈现了各模型在生成数据上的拟合指标。根据值, 各模型均拟合生成数据, 即联合模型中结构模型的有偏设定不太影响测量模型对数据的绝对拟合。根据DIC值发现, 当JRT- PINC作为数据生成模型时, 其DIC与两个CJRT- PINC的DIC均接近; 而当任一CJRT-PINC作为数据生成模型时, CJRT-PINC对数据的拟合明显优于JRT-PINC的, 这表明引入交叉负载的联合模型的适用范围更广。另外, 当CJRT-PINC-θ作为数据生成模型时, 两个CJRT-PINC的DIC与JRT-PINC的DIC之间的差值在1,000左右; 而当CJRT-PINC-作为数据生成模型时, 两个CJRT-PINC的DIC与JRT-PINC的DIC之间的差值仅为100左右。该结果表明CJRT-PINC-θ的普适性相对更高：当其他两个模型为数据生成模型时, 它能够提供与数据生成模型几乎一致的拟合指标; 而当它作为数据生成模型时, 其他两个模型对数据的拟合则相对要差一些。另外, 各模型参数的返真性也呈现类似的趋势(见网络版附录表S4.1～S4.4)。总之, 研究3结果表明(1)忽略可能存在的交叉负载所导致的负面结果比冗余考虑存在交叉负载所导致的更严重, 即CJRT-PINC对测验情境的兼容性优于JRT-PINC; 且(2) CJRT-PINC-θ的普适性相对于CJRT-PINC-更高。

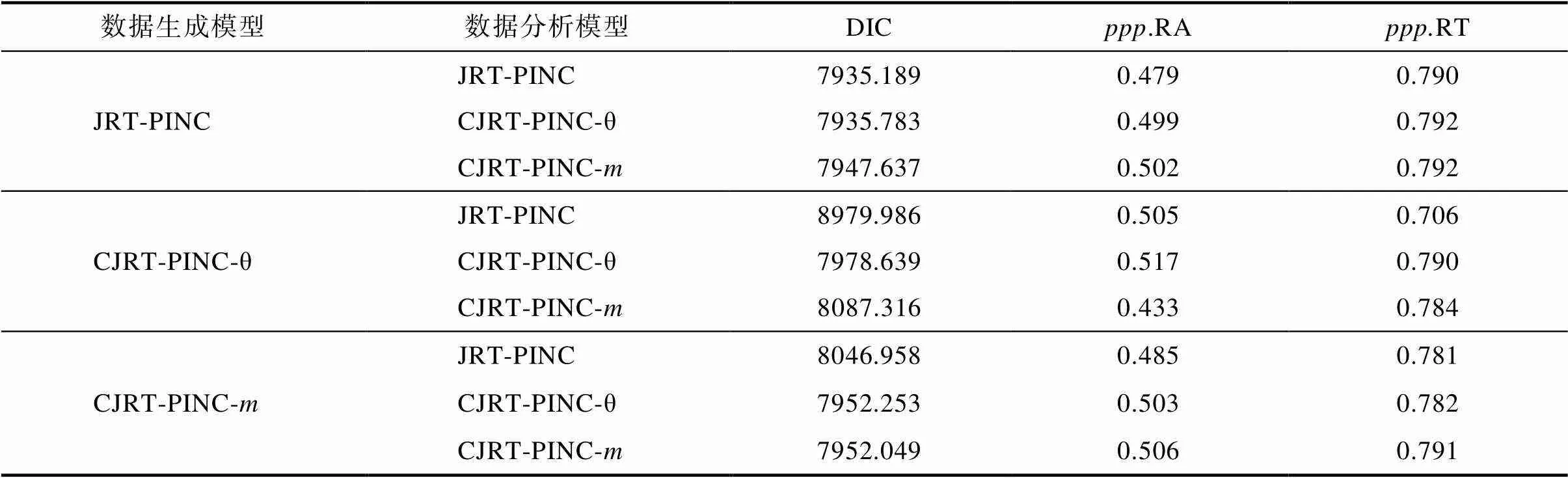
表5 研究3中模型−数据相对拟合情况

注：DIC = deviance information criterion;.RA = RA的后验预测概率;.RT = RT的后验预测概率。

6 实证数据分析

6.1 数据描述

本节以PISA 2012年计算机化数学测验数据为例进一步展现新模型在实践中的可应用性。测验数据共包含32个国家, 研究从中选取了4个国家/地区：中国上海(QCN)、美国(USA)、新加坡(SGP)和斯洛伐克共和国(SVK)。初始样本量为1754人, 清理后数据包含= 1597名被试。PISA 2012的数学测验框架(OECD, 2013)已公开的10道题目共包含7个属性(Zhan, Jiao, & Liao, 2018), 分别是：(K1)变化和关系、(K2)数量、(K3)空间与图形、(K4)不确定性和数据、(K5)与职业相关的背景、(K6)与社会相关的背景以及(K7)与科学相关的背景。测验Q矩阵见网络版附录表S5.1。另外, CM015Q02D、CM015Q03D和CM020Q01三道题目原为多级评分题目(0, 1, 2), 由于本研究的模型仅针对二级评分数据(0, 1), 因此对这三题的作答结果采用Zhan, Jiao和Liao (2018)的编码方式：0和1编码为0, 2编码为1。

6.2 分析与评价指标

分别使用JRT-PINC、CJRT-PINC-θ、CJRT- PINC-和另外两个已有模型分析该数据——包括仅可分析RA的HO-PINC和基于确定态属性的联合作答与时间DINA (joint responses and times DINA, JRT-DINA; Zhan, Jiao, & Liao, 2018)。采用DIC统计量作为模型−数据相对拟合指标,作为模型−数据绝对拟合指标。

6.3 结果

表6呈现了各模型在测验数据上的拟合指标。需要注意的是, 由于CJRT-PINC-中有约42.75%的待估计参数(包括m, s, g, κ, λ0k, λ1k, ξ, σβδ, σβκ, σδκ)未达到收敛标准(PSRF < 1.2), 因此该模型与数据的拟合结果仅供参考, 后续不在文中进行探讨。由结果可知, 所有模型的值均在0.5左右, 表示各模型均拟合测验数据。根据DIC指标, 基于概率态属性的三个联合模型对数据的拟合均优于基于确定态属性的JRT-DINA的。同时, 基于联合−交叉负载建模框架的两个CJRT-PINC对数据的拟合优于基于联合−层级建模框架的JRT-PINC。下文将主要基于对数据拟合相对最好的CJRT-PINC-θ的分析结果进行阐述。

表6 实证数据中模型−数据拟合指标

注：DIC = deviance information criterion;.RA = RA的后验预测概率;.RT = RT的后验预测概率; HO-PINC分析的数据量少于另外4个联合模型, 所以其DIC值不具有可比性。

表7呈现了CJRT-PINC-θ在测验数据中交叉负载φ的后验均值和置信区间, 以及其他题目参数的后验均值。结果显示交叉负载φ后验均值的估计范围在−0.027到0.338之间, 所有题目上的交叉负载95%置信区间都不包含零。题目1和9的φ< 0, 表明这两个题目上能力越高的被试作答题目的时间越短, 其他题目则相反(φ> 0)。该结果整体与JRT-PINC的基本一致, JRT-PINC中能力与加工速度呈负相关(ρθτ= −0.531), 表示能力越高的被试加工速度越慢(作答题目的时间越长)。能力与加工速度负相关结果可能是因为PISA属于低风险/低动机的测验, 其结果对于学生而言影响较小因此学生的作答动机较低, 这一结论与已有研究(Zhan, Jiao, & Liao, 2018)的结果一致。此外CJRT-PINC-θ中各题目的交叉负载估计值之间并不一致, 表明各题目的RT为能力提供的辅助信息量具有差异性, 单凭JRT-PINC中的一个笼统相关系数可能无法较好地处理该情况。另外, 我们计算了交叉负载和其他3个题目参数之间的相关系数, 发现交叉负载与失误参数的相关系数最高(0.923), 与时间强度参数的相关系数次之(0.622), 与猜测参数的相关系数最低(−0.599); 结果表明题目的失误参数越高, RT为能力提供的辅助信息越高; 当然, 这种关系只是该数据特有的, 结论的推广性有待进一步验证。

表8呈现了JRT-PINC, CJRT-PINC-θ, JRT-DINA和HO-PINC对个体的分析结果。4个模型的诊断结构具有一定的一致性, 但同时存在差异。首先, 当概率态属性估计结果大于0.5时, 确定态属性的诊断结果也多为“1”。其次, 基于概率态属性的两个模型比基于确定态属性的JRT-DINA能更精细地反馈出学生对属性的掌握情况及个体差异性。以被试59为例, JRT-DINA诊断被试的属性2为掌握“1”, 但此时概率态属性结果显示被试对属性2的掌握概率仅略高于0.5, 距离熟练/完全掌握还有一定距离, 还需要进一步干预。再次, 与HO-PINC相比, 三个考虑RT信息的联合模型均可以提供有关加工速度的估计值, 丰富了反馈报告的内容。

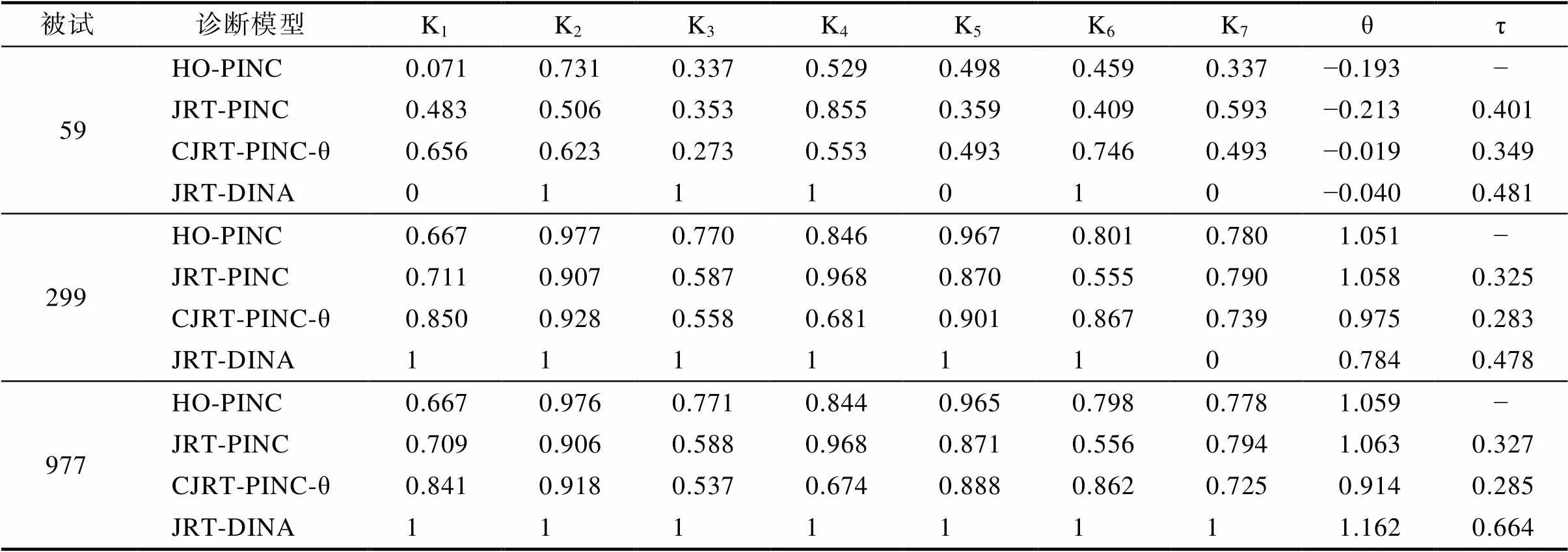
表8 实证数据中各模型对个体属性的诊断结果示例

7 总结、讨论与展望

7.1 总结与讨论

随着实践者对精细化诊断需求的不断增加, 传统基于确定态属性的CDM已显得力不从心, 概率态CDM应运而生。但是已有的概率态CDM仍然延续传统的建模方式, 无法实现同时分析多模态数据(比如, RA和RT)。对此, 本文基于两种可联合分析RA和RT的认知诊断建模框架提出了三个联合概率态CDM：JRT-PINC、CJRT-PINC-θ和CJRT- PINC-。其中, JRT-PINC是基于联合−层级认知诊断建模框架构建的, 但该模型需要满足较多的条件独立性假设以保证模型的可识别性; 另外两个CJRT-PINC是基于联合−交叉负载认知诊断建模框架构建的, 它们释放了JRT-PINC中部分条件独立性假设, 增加了适用范围。三个新模型均具有概率态CDM的优点, 可以实现对属性掌握状态的精细化诊断, 有益于区分被试间的个体差异, 为因材施教和精准教学提供数据支持; 同时, 作为一种联合模型, 三者均可利用RT中所包含的信息提高模型参数估计精度, 并反馈个体加工速度, 丰富诊断反馈信息。

本文通过三个模拟研究探讨了新模型在不同模拟条件下的心理计量学性能。模拟研究结果主要表明：(1)三个新模型的参数估计返真性均较好; (2)额外引入RT, 不仅有助于提高模型参数估计精度还可提供有关个体加工速度的测量; (3) CJRT-PINC-θ比CJRT-PINC-更充分地利用RT所包含信息去提高核心建构(能力和属性)的参数估计精度; (4)忽略交叉负载所导致的负面结果比冗余考虑交叉负载所导致的更严重。然后, 本文以一则实证数据为例对比探究了5个CDM的表现, 包括3个联合概率态模型(JRT-PINC、CJRT-PINC-θ、CJRT-PINC-)、1个联合确定态模型(JRT-DINA)和1个仅分析RA的概率态模型(HO-PINC)。研究结果表明(1)相比于确定态属性, 概率态属性可以更精细化地反馈被试对属性的掌握情况; (2)基于联合−交叉负载认知诊断建模框架构建的CJRT-PINC比基于联合−层级认知诊断建模框架构建的JRT-PINC更拟合该数据; (3)额外引入RT, 可丰富诊断反馈内容, 提供有关被试加工速度的测量。

综上, 新模型的提出丰富了概率态CDM的适用范围, 为后续进一步在技术增强型测评系统中联合分析多模态数据进行精细化全面化诊断提供了方法学引导。当然, 本研究仅在有限的范围内探讨并展现了三个联合概率态CDM的表现。由于任何模型都有其适用的测验情境, 本研究并没有否定其他对比模型, 更多地是进一步丰富现有的认知诊断模型可选项。在实践中, 可使用数据驱动方法, 依据模型−数据相对拟合指标来选择合适的模型。

7.2 局限与展望

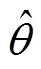
《深化新时代教育评价改革总体方案》中提出“改进结果评价, 强化过程评价, 探索增值评价, 健全综合评价”; 在“改进结果评价”的基础上, 未来可面向过程评价、增值评价和综合评价, 进一步尝试拓展本文提出的模型, 比如：

(1) “强化过程评价”取向。概率态属性的一个有价值的实践用途是描述被试对属性的掌握状况的精细化变化(Zhan, 2021)。本研究暂局限于横断测验, 未关注被试潜在特质的动态发展变化。未来可尝试结合已有的纵向认知诊断建模, 进一步探索概率态属性和加工速度的动态变化。

(2) “探索增值评价”取向。CDM主要关注对个体水平特质的测量, 暂未关注对教师和学校层面的投入的评价。结合“过程评价”取向的未来成果, 精细化诊断适宜于刻画学生的发展变化, 不仅有助于肯定学生的努力付出, 也有助于准确反映教师和学校的投入, 进而有利于实现基于学生学习进步来评价教师教学绩效的主张(张莉娜等, 2022)。

(3) “健全综合评价”取向。本研究对多模态数据的利用尚不够充分, 局限于RA和RT两种数据, 进而仅能提供与认知能力和加工速度有关的诊断反馈。随着信息技术及测量方式的发展, 技术增强型测评已经可以获取学生问题解决过程中的多模态数据(如, 眼动数据、鼠标点击次数、行动序列, 以及面部表情、动作和心率等变化数据), 后续可以将更多模态的数据纳入分析中(如, Zhan et al., 2022), 以丰富数据分析结果所包含的信息, 为全面化、多元化的综合评价提供方法学支持。

Bolsinova, M., de Boeck, P., & Tijmstra, J. (2017). Modelling conditional dependence between response time and accuracy., 1126−1148.

Bolsinova, M., & Tijmstra, J. (2018). Improving precision of ability estimation: Getting more from response times.(1), 13−38.

Bradshaw, L., & Levy, R. (2019). Interpreting probabilistic classifications from diagnostic psychometric models.,(2), 79−88.

de Boeck, P., & Jeon, M. (2019). An overview of models for response times and processes in cognitive tests., 102.

de la Torre, J., & Douglas, J. (2004). Higher-order latent trait models for cognitive diagnosis.333−353.

Guo, L. Shang, P., & Xia, L. (2017). Advantages and illustrations of application of response time model in psychological and educational testing.(4), 701−712.

[郭磊, 尚鹏丽, 夏凌翔. (2017). 心理与教育测验中反应时模型应用的优势与举例.(4), 701−712.]

Huang, H.-Y. (2020). Utilizing response times in cognitive diagnostic computerized adaptive testing under the higher-order deterministic input, noisy ‘and’ gate model.(1), 109−141.

Liu, Q., Wu, R. Z., Chen, E. H., Xu, G. D., Su, Y., Chen, Z. G., & Hu, G. P. (2018). Fuzzy cognitive diagnosis for modelling examinee performance.(4), Article 48.

Mao, X. (2014). The attribute mastery probability cognitive diagnostic model.(3), 437−443.

[毛秀珍. (2014). 基于属性掌握概率的认知诊断模型.(3), 437−443.]

Meng, X., Tao, J., & Chang, H.-H. (2015). A conditional joint modeling approach for locally dependent item responses and response times.(1), 1−27.

OECD. (2013).OECD Publishing.

Peng, S., Cai, Y., Wang, D., Luo, F., & Tu, D. (2022). A generalized diagnostic classification modeling framework integrating differential speediness: Advantages and illustrations in psychological and educational testing.(6), 940−959.

Ranger, J. (2013). A note on the hierarchical model for responses and response times in tests of van der Linden (2007).(3), 538−544

Tang, F., & Zhan, P. (2021). Does diagnostic feedback promote learning? Evidence from a longitudinal cognitive diagnostic assessment.(1), 1−15.

Tatsuoka, K. K. (1983). Rule Space: An approach for dealing with misconceptions based on item response theory.,(4), 345−354.

van der Linden, W. J. (2006). A lognormal model for response times on test items.(2), 181−204.

van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items., 287−308.

Wang, C., & Xu, G. (2015). A mixture hierarchical model for response times and response accuracy.(3), 456−477.

Xu, G., & Zhang, S. (2016). Identifiability of diagnostic classification models., 625−649.

Yan, J. H. (2010). Cognitive styles affect choice response time and accuracy., 747−751.

Zhan, P. (2021). Refined learning tracking with a longitudinal probabilistic diagnostic model.(1), 44−58.

Zhan, P. (2022). Joint-cross-loading multimodal cognitive diagnostic modeling incorporating visual fixation counts.(11), 1416−1423

[詹沛达. (2022). 引入眼动注视点的联合-交叉负载多模态认知诊断建模.(11), 1416−1423]

Zhan, P., & Bian, Y. (2015). The probabilistic-inputs, noisy “and” gate model.(5), 1230−1238.

[詹沛达, 边玉芳. (2015). 概率性输入, 噪音“与”门(PINA)模型.(5), 1230−1238.]

Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times.(2), 262−286.

Zhan, P., Jiao, H., Man, K., & Wang, L. (2019). Using JAGS for Bayesian cognitive diagnosis modeling: A tutorial.(4), 473−503.

Zhan, P., Man, K., Wind, S. A., & Malone, J. (2022). Cognitive diagnosis modelling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis.(6), 736rnal.

Zhan, P., Tian, Y., Yu, Z., Li, F., & Wang, L. (2020). A comparative study of probabilistic logic and fuzzy logic in refined learning diagnosis., 1258−1266.

[詹沛达, 田亚淑, 于照辉, 李菲茗, 王立君. (2020). 概率逻辑与模糊逻辑在精细化学习诊断中的对比研究., 1258−1266.]

Zhan, P., Wang, W. C., Jiao, H., & Bian, Y. F. (2018). Probabilistic-input, noisy conjunctive models for cognitive diagnosis., 997.

Zhang, L., Zhong, Z., Liu, H., & You, X. (2022). Exploration and reflection on teachers' performance appraisal in the context of educational evaluation reform-based on the perspective of value-added evaluation., 23−39.

[张莉娜, 钟祖荣, 刘红云, 游晓锋. (2022). 教育评价改革背景下教师绩效考评的探索与思考——基于增值评价的视角., 23−39.]

Zheng, T., Zhou, W., & Guo, L. (2023). Cognitive diagnosis modelling based on response times.,(2), 478−490.

[郑天鹏, 周文杰, 郭磊. (2023). 基于题目作答时间信息的认知诊断模型.,(2), 478−490.]

首先, 根据条件独立性假设,X和logT满足：

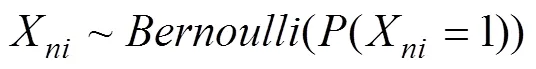
其次, 假设被试参数先验分布为：

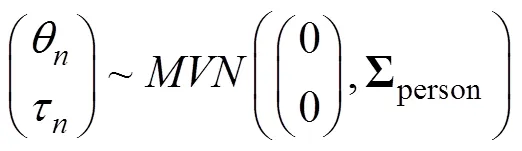
为了使模型可识别, 约束μθ= 0, μτ= 0, 以及σθ= 1 (Guo et al., 2020; Meng, Tao, & Chang, 2015; van der Linden, 2007; Zhan et al., 2018)。由于矩阵中σθ= 1不能直接使用逆Wishart分布(inverse-Wishart), 因此需要对Σperson进行Cholesky分解(Zhan et al., 2018), 即：

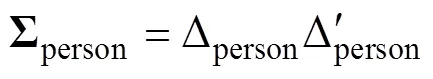
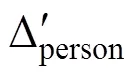
此外, 高阶结构参数的先验分布设定为：λ0k～(0, 4), λ1k～N(0, 4)。

最后, 假设题目参数先验分布为：

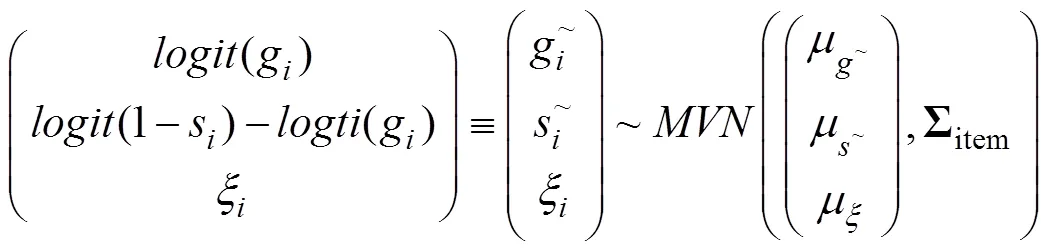
其中各参数的超先验设定为：

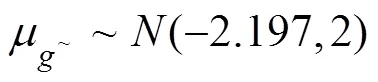
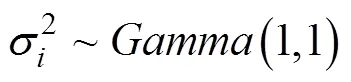
由于CJRT-PINC-θ中潜在能力和速度参数为独立分布, 因此假设被试参数先验分布为：

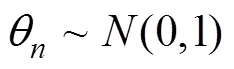
假设题目参数先验分布为：

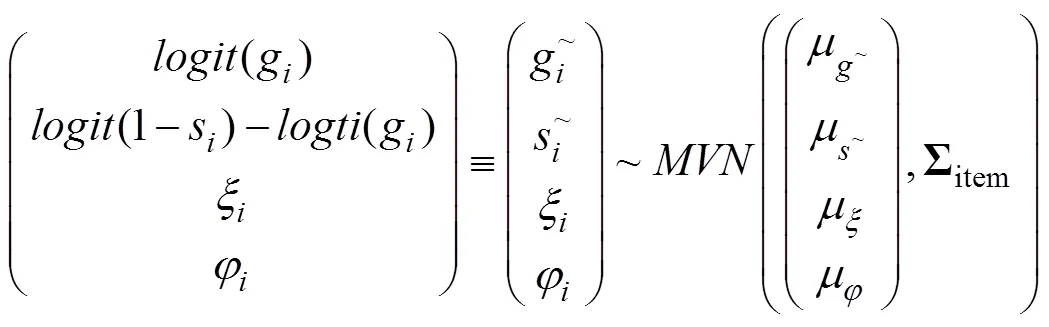
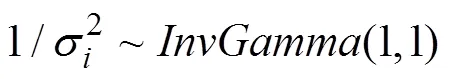
低信息量先验分布的设定以“无知”为前提, 并以大方差(如, 5)为变异范围。由于S1.1中部分参数已经采用低信息量先验或超先验, 所以在S1.1的基础上, 部分参数的低信息量先验分布设定如下：

其他参数的先验分布保持不变。

选用正文模拟研究中= 200,= 15条件下生成的数据作为分析模型, Q矩阵见正文图3; 该模拟条件属于小样本短测验情境, 理论上参数估计结果受到先验分布的影响更大。随样本量增大及测验长度提高, 参数估计结果受先验分布中所含信息量的影响会逐渐降低(即鲁棒性会增加)。另外, 对于JRT-PINC模型, 设定潜在能力与加工速度的相关系数ρθτ= 0.5; 对于JRT-PINC-θ, 设定交叉负载(φ)满足均值为0.5、方差为0.15的正态分布; 对于, JRT-PINC-, 设定交叉负载(κ)满足均值为0.5、方差为0.15的正态分布。三个模型的其他参数设定与正文研究中保持一致, 且参数估计设定(如, 马尔可夫链长)与各模拟研究中保持一致。

表S1.1到表S1.3呈现了3个模型在不同信息量先验分布下各参数的返真性。整体而言, 基于研究经验设定的正常信息量先验分布下的参数估计返真性与低信息量先验分布下的参数估计返真性具有较高的一致性, 且前者略优于后者。另外, 三个模型中, CJRT-PINC-θ受先验分布信息量的影响略大于另外两个模型。

表S1.1 不同信息量先验分布下被试参数的估计一致性

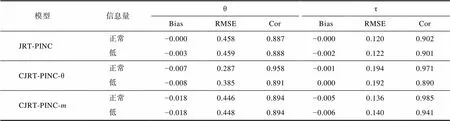
模型信息量θτ BiasRMSECorBiasRMSECor JRT-PINC正常−0.0000.4580.887−0.0000.1200.902 低−0.0030.4590.888−0.0020.1220.901 CJRT-PINC-θ正常−0.0070.2870.958−0.0010.1940.971 低−0.0080.3850.8910.0000.1920.890 CJRT-PINC-m正常−0.0180.4460.894−0.0050.1360.985 低−0.0180.4480.894−0.0060.1400.941

表S1.2 不同信息量先验分布下属性的估计一致性

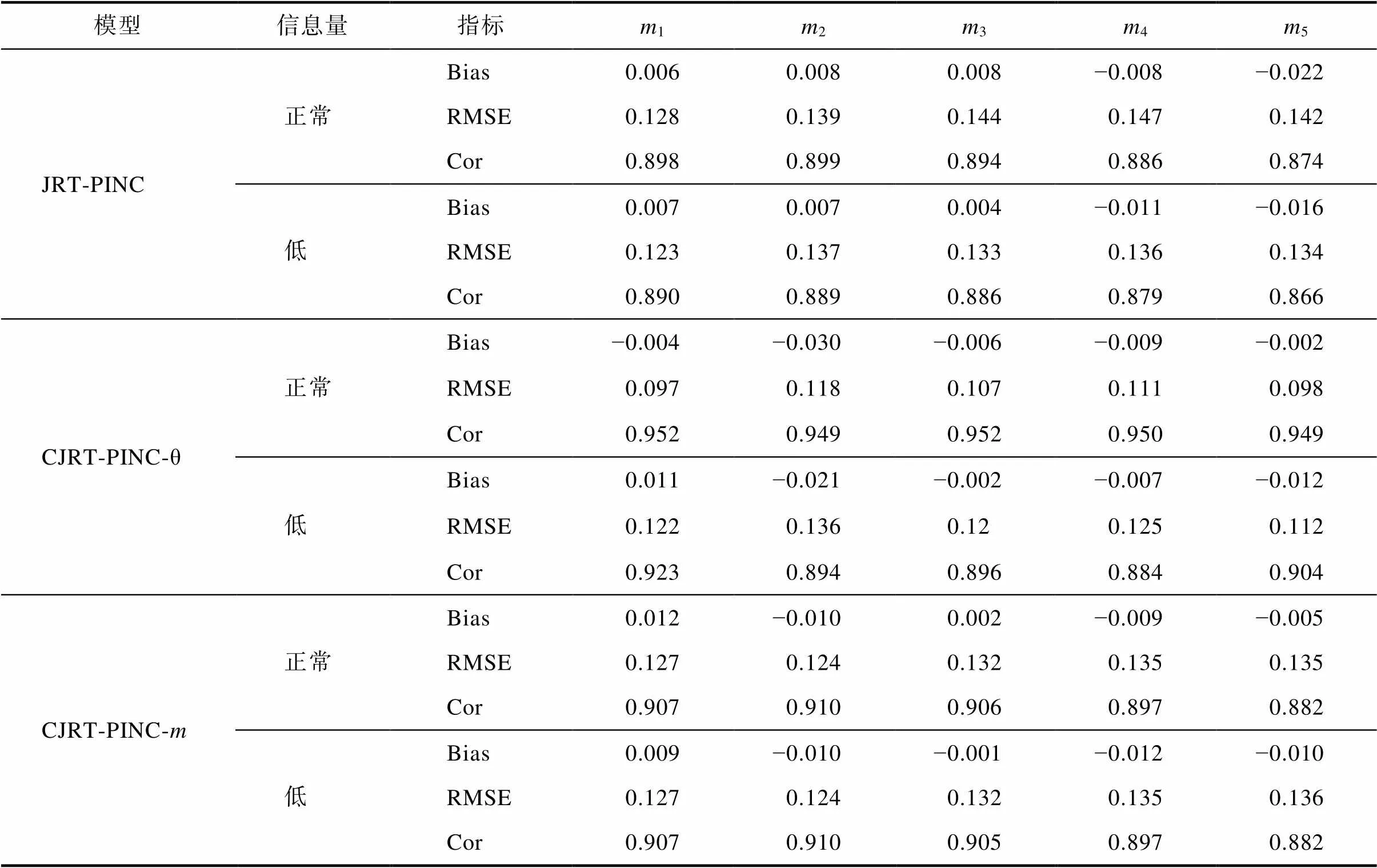
模型信息量指标m1m2m3m4m5 JRT-PINC正常Bias0.0060.0080.008−0.008−0.022 RMSE0.1280.1390.1440.1470.142 Cor0.8980.8990.8940.8860.874 低Bias0.0070.0070.004−0.011−0.016 RMSE0.1230.1370.1330.1360.134 Cor0.890 0.889 0.886 0.879 0.866 CJRT-PINC-θ正常Bias−0.004−0.030−0.006−0.009−0.002 RMSE0.097 0.118 0.1070.1110.098 Cor0.9520.9490.9520.9500.949 低Bias0.011−0.021−0.002−0.007−0.012 RMSE0.1220.1360.120.1250.112 Cor0.923 0.894 0.896 0.884 0.904 CJRT-PINC-m正常Bias0.012−0.0100.002−0.009−0.005 RMSE0.1270.1240.1320.1350.135 Cor0.9070.9100.9060.8970.882 低Bias0.009−0.010−0.001−0.012−0.010 RMSE0.1270.1240.1320.1350.136 Cor0.9070.9100.9050.8970.882

表S1.3 不同信息量先验分布下属性的估计一致性

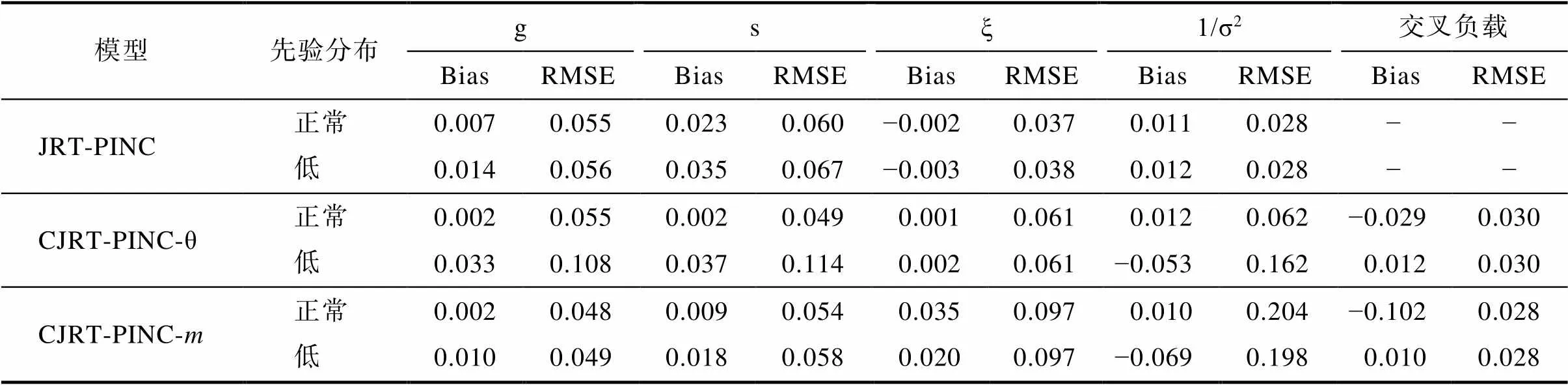
模型先验分布gsξ1/σ2交叉负载 BiasRMSEBiasRMSEBiasRMSEBiasRMSEBiasRMSE JRT-PINC正常0.0070.0550.0230.060−0.002 0.0370.011 0.028−− 低0.0140.0560.0350.067−0.0030.0380.0120.028−− CJRT-PINC-θ正常0.0020.0550.0020.0490.0010.0610.0120.062−0.0290.030 低0.0330.1080.0370.1140.0020.061−0.0530.1620.0120.030 CJRT-PINC-m正常0.0020.0480.0090.0540.0350.0970.0100.204−0.1020.028 低0.0100.0490.0180.0580.0200.097−0.0690.1980.0100.028

表S2.1 研究1中概率态属性参数估计的平均Bias

注: JRT-PINC = 联合−层级概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; θ = 高阶潜在能力; τ = 加工速度; N = 样本量; I = 题目数量; ρ = 能力与速度之间相关。

表S2.2 研究1中题目参数的返真性

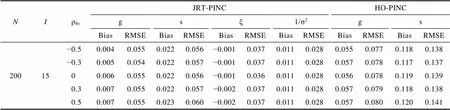
NIρθτJRT-PINCHO-PINC gsξ1/σ2gs BiasRMSEBiasRMSEBiasRMSEBiasRMSEBiasRMSEBiasRMSE 20015−0.50.004 0.0550.0220.056−0.001 0.0370.0110.0280.0550.0770.1180.138 −0.30.005 0.0540.0220.057−0.001 0.0370.0110.0280.0570.0780.1170.137 00.006 0.0550.0220.056−0.001 0.0360.0110.0280.0560.0780.1190.139 0.30.007 0.0550.0220.057−0.002 0.0370.0110.0280.0570.0790.1180.138 0.50.007 0.0550.0230.060−0.002 0.0370.0110.0280.0570.0800.1200.141

续表S2.2

NIρθτJRT-PINCHO-PINC gsξ1/σ2gs BiasRMSEBiasRMSEBiasRMSEBiasRMSEBiasRMSEBiasRMSE 30−0.50.005 0.0430.0130.051−0.002 0.0340.0120.0290.0430.0610.1220.143 −0.30.004 0.0440.0130.051−0.003 0.0340.0120.0290.0420.0610.1240.146 00.005 0.0440.0130.049−0.002 0.0340.0120.0290.0430.0620.1230.145 0.30.005 0.0430.0140.049−0.004 0.0350.0120.0290.0430.0620.1230.145 0.50.004 0.0430.0130.050−0.003 0.0340.0120.0290.0430.0610.1240.145 50015−0.50.006 0.0430.0110.0440.000 0.0220.0040.0170.0460.0610.0830.099 −0.30.006 0.0440.0100.043−0.001 0.0220.0040.0170.0470.0610.0830.099 00.007 0.0440.0090.045−0.000 0.0220.0040.0170.0490.0630.0840.101 0.30.008 0.0450.0100.045−0.001 0.0220.0040.0170.0490.0630.0820.100 0.50.006 0.0440.0080.045−0.000 0.0220.0040.0170.0490.0640.0830.100 30−0.5−0.000 0.0290.0020.0370.000 0.0210.0050.0170.0270.0390.0800.095 −0.30.000 0.0290.0030.0360.000 0.0220.0050.0170.0270.0390.0800.096 0−0.001 0.0290.0030.0370.001 0.0210.0050.0170.0270.0390.0790.094 0.3−0.001 0.0290.0010.0350.000 0.0220.0050.0170.0260.0380.0780.093 0.5−0.002 0.0290.0000.0350.001 0.0220.0050.0170.0260.0380.0780.093

表S2.3 研究1中方差协方差矩阵和题目均值向量的平均Bias

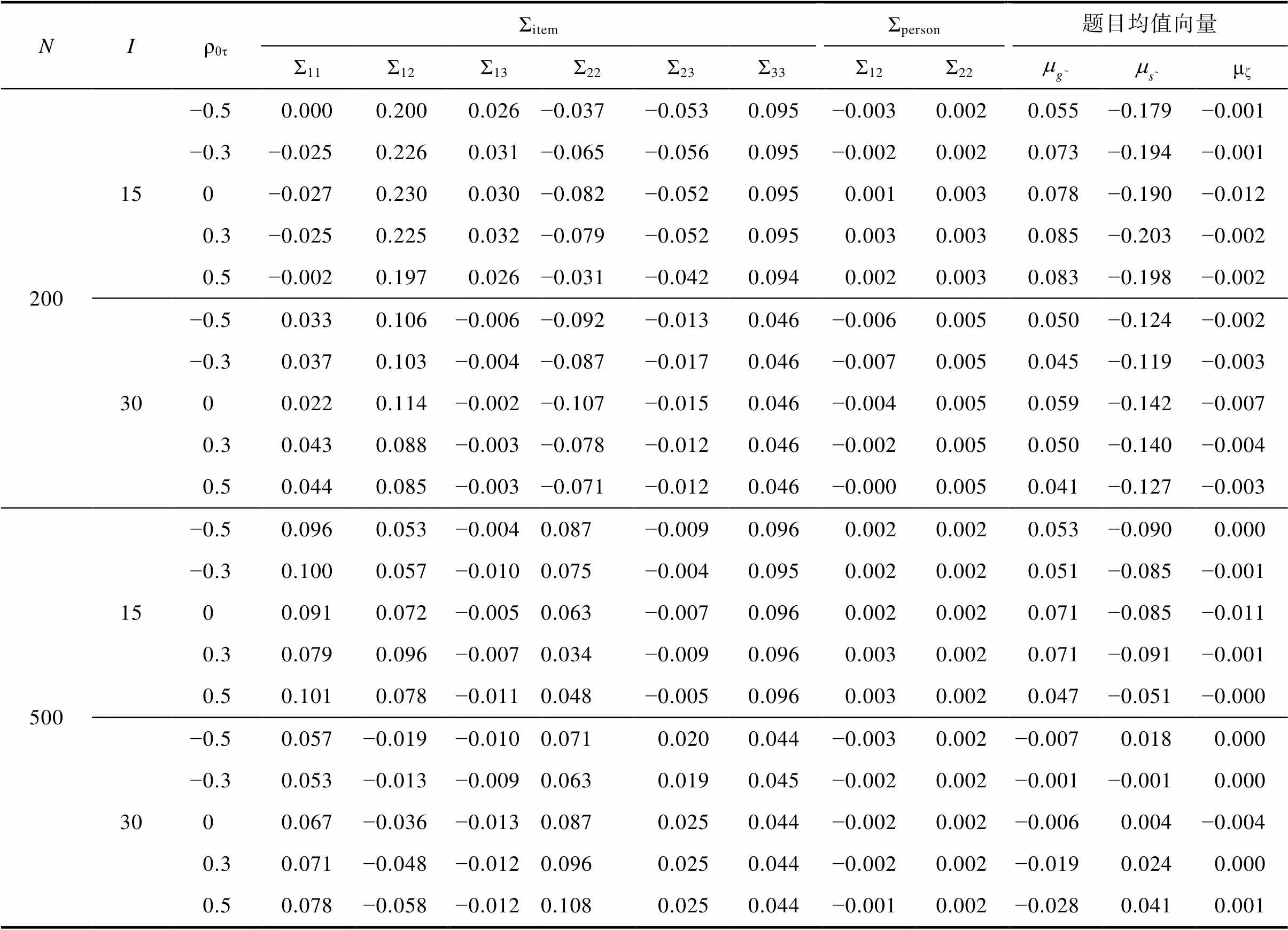
NIρθτΣitemΣperson题目均值向量 Σ11Σ12Σ13Σ22Σ23Σ33Σ12Σ22μζ 20015−0.50.000 0.200 0.026 −0.037 −0.053 0.095−0.003 0.0020.055 −0.179 −0.001 −0.3−0.025 0.226 0.031 −0.065 −0.056 0.095−0.002 0.0020.073 −0.194 −0.001 0−0.027 0.230 0.030 −0.082 −0.052 0.0950.001 0.0030.078 −0.190 −0.012 0.3−0.025 0.225 0.032 −0.079 −0.052 0.0950.003 0.0030.085 −0.203 −0.002 0.5−0.002 0.197 0.026 −0.031 −0.042 0.0940.002 0.0030.083 −0.198 −0.002 30−0.50.033 0.106 −0.006 −0.092 −0.013 0.046−0.006 0.0050.050 −0.124 −0.002 −0.30.037 0.103 −0.004 −0.087 −0.017 0.046−0.007 0.0050.045 −0.119 −0.003 00.022 0.114 −0.002 −0.107 −0.015 0.046−0.004 0.0050.059 −0.142 −0.007 0.30.043 0.088 −0.003 −0.078 −0.012 0.046−0.002 0.0050.050 −0.140 −0.004 0.50.044 0.085 −0.003 −0.071 −0.012 0.046−0.000 0.0050.041 −0.127 −0.003 50015−0.50.096 0.053 −0.004 0.087 −0.009 0.0960.002 0.0020.053 −0.090 0.000 −0.30.100 0.057 −0.010 0.075 −0.004 0.0950.002 0.0020.051 −0.085 −0.001 00.091 0.072 −0.005 0.063 −0.007 0.0960.002 0.0020.071 −0.085 −0.011 0.30.079 0.096 −0.007 0.034 −0.009 0.0960.003 0.0020.071 −0.091 −0.001 0.50.101 0.078 −0.011 0.048 −0.005 0.0960.003 0.0020.047 −0.051 −0.000 30−0.50.057 −0.019 −0.010 0.071 0.020 0.044−0.003 0.002−0.007 0.018 0.000 −0.30.053 −0.013 −0.009 0.063 0.019 0.045−0.002 0.002−0.001 −0.001 0.000 00.067 −0.036 −0.013 0.087 0.025 0.044−0.002 0.002−0.006 0.004 −0.004 0.30.071 −0.048 −0.012 0.096 0.025 0.044−0.002 0.002−0.019 0.024 0.000 0.50.078 −0.058 −0.012 0.108 0.025 0.044−0.001 0.002−0.028 0.041 0.001

表S2.4 研究1中方差协方差矩阵和题目均值向量的平均RMSE

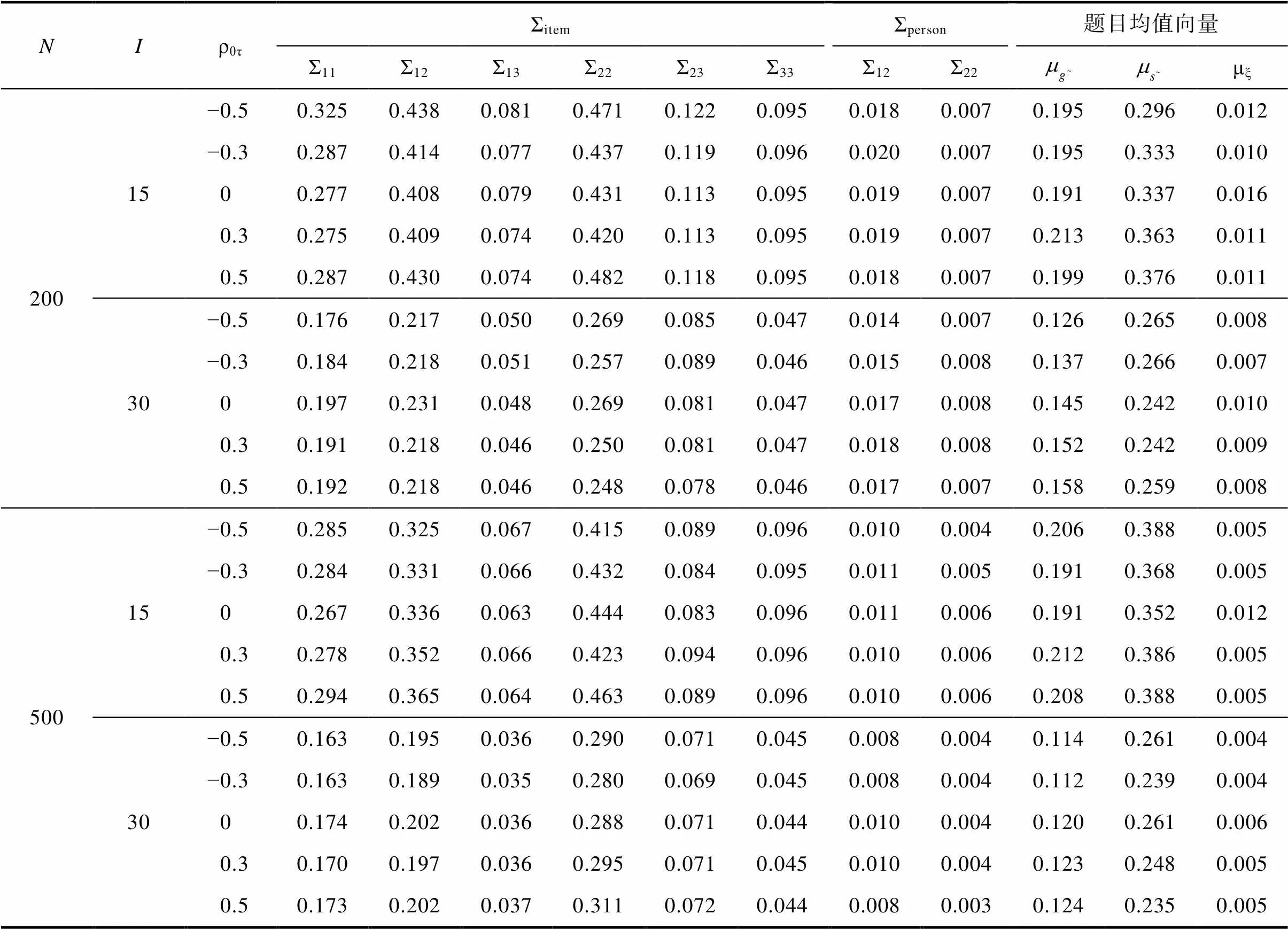
NIρθτΣitemΣperson题目均值向量 Σ11Σ12Σ13Σ22Σ23Σ33Σ12Σ22μξ 20015−0.50.3250.4380.0810.4710.1220.0950.0180.0070.1950.2960.012 −0.30.2870.4140.0770.4370.1190.0960.0200.0070.1950.3330.010 00.2770.4080.0790.4310.1130.0950.0190.0070.1910.3370.016 0.30.2750.4090.0740.4200.1130.0950.0190.0070.2130.3630.011 0.50.2870.4300.0740.4820.1180.0950.0180.0070.1990.3760.011 30−0.50.1760.2170.0500.2690.0850.0470.0140.0070.1260.2650.008 −0.30.1840.2180.0510.2570.0890.0460.0150.0080.1370.2660.007 00.1970.2310.0480.2690.0810.0470.0170.0080.1450.2420.010 0.30.1910.2180.0460.2500.0810.0470.0180.0080.1520.2420.009 0.50.1920.2180.0460.2480.0780.0460.0170.0070.1580.2590.008 50015−0.50.2850.3250.0670.4150.0890.0960.0100.0040.2060.3880.005 −0.30.2840.3310.0660.4320.0840.0950.0110.0050.1910.3680.005 00.2670.3360.0630.4440.0830.0960.0110.0060.1910.3520.012 0.30.2780.3520.0660.4230.0940.0960.0100.0060.2120.3860.005 0.50.2940.3650.0640.4630.0890.0960.0100.0060.2080.3880.005 30−0.50.1630.1950.0360.2900.0710.0450.0080.0040.1140.2610.004 −0.30.1630.1890.0350.2800.0690.0450.0080.0040.1120.2390.004 00.1740.2020.0360.2880.0710.0440.0100.0040.1200.2610.006 0.30.1700.1970.0360.2950.0710.0450.0100.0040.1230.2480.005 0.50.1730.2020.0370.3110.0720.0440.0080.0030.1240.2350.005

表S3.1 研究2 (子研究1)中题目参数的返真性

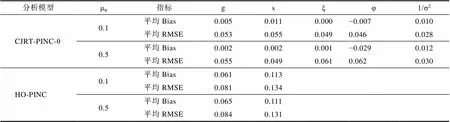
分析模型μφ指标gsξφ1/σ2 CJRT-PINC-θ0.1平均Bias0.0050.0110.000−0.0070.010 平均RMSE0.0530.0550.0490.0460.028 0.5平均Bias0.0020.0020.001−0.0290.012 平均RMSE0.0550.0490.0610.0620.030 HO-PINC0.1平均Bias0.0610.113 平均RMSE0.0810.134 0.5平均Bias0.0650.111 平均RMSE0.0840.131

表S3.2 研究2 (子研究1)中题目参数方差协方差矩阵和均值向量的返真性

μφ指标Σitem题目均值向量 Σ11Σ12Σ13Σ22Σ23Σ33μζ 0.1平均Bias−0.0540.2410.025−0.124−0.0420.0940.081−0.0930.000 平均RMSE0.3100.4060.0800.3670.1210.0950.2280.3950.027 0.5平均Bias−0.0230.1720.0090.058−0.0100.0940.0420.0430.001 平均RMSE0.2520.3740.0780.4720.1230.0940.2160.4110.045

为了更符合实际测试的复杂情境, 研究设置不同题目中理想作答概率对RT的影响不同, 因此数据生成中设定自变量交叉负载(κ)满足方差为0.15的正态分布, 其中低影响效应μκ= 0.1, 高影响效应μκ= 0.5。其余参数设定与研究1和研究2 (子研究1)相同。根据CJRT-PINC-(正文公式2～3和10～11)生成所有被试在所有题目上的RA和RT。

使用CJRT-PINC-和HO-PINC分析该数据。结果显示所有参数的PSRF均小于1.2, 表示各参数均已收敛。附录表S3.3呈现了能力参数与加工速度参数的返真性, 附录表S3.4呈现了属性参数的返真性。首先, CJRT-PINC-对所有参数的返真性均优于HO-PINC的。其次, 在CJRT-PINC-中, 由于RT没有为能力直接提供信息, 所以能力参数的RMSE与研究1中JRT-PINC的基本一致。再有, 随着交叉负载均值提高, 能力、加工速度和属性的返真性均有所提高。题目参数和方差协方差矩阵参数的返真性见附录表S3.5和表S3.6。整体而言, CJRT-PINC-在不同模拟条件下模型参数的返真性良好, 均优于不考虑RT的HO-PINC的。

表S3.3 研究2 (子研究2)中被试参数估计返真性

分析模型μφθτ BiasRMSECorBiasRMSECor CJRT-PINC-m0.1−0.0070.4610.8870.0000.1350.978 0.5−0.0180.4460.894−0.0050.1360.985 HO-PINC0.1−0.0090.4820.876 0.5−0.0200.4800.875

注: CJRT-PINC-= 基于属性的联合−交叉负载概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; θ = 能力; τ = 加工速度; μφ= 交叉负载均值; Bias = 所有被试的平均偏差; RMSE = 所有被试的平均均方根误差; Cor = 估计值与真值之间的相关系数。

表S3.4 研究2 (子研究2)概率态属性参数估计返真性

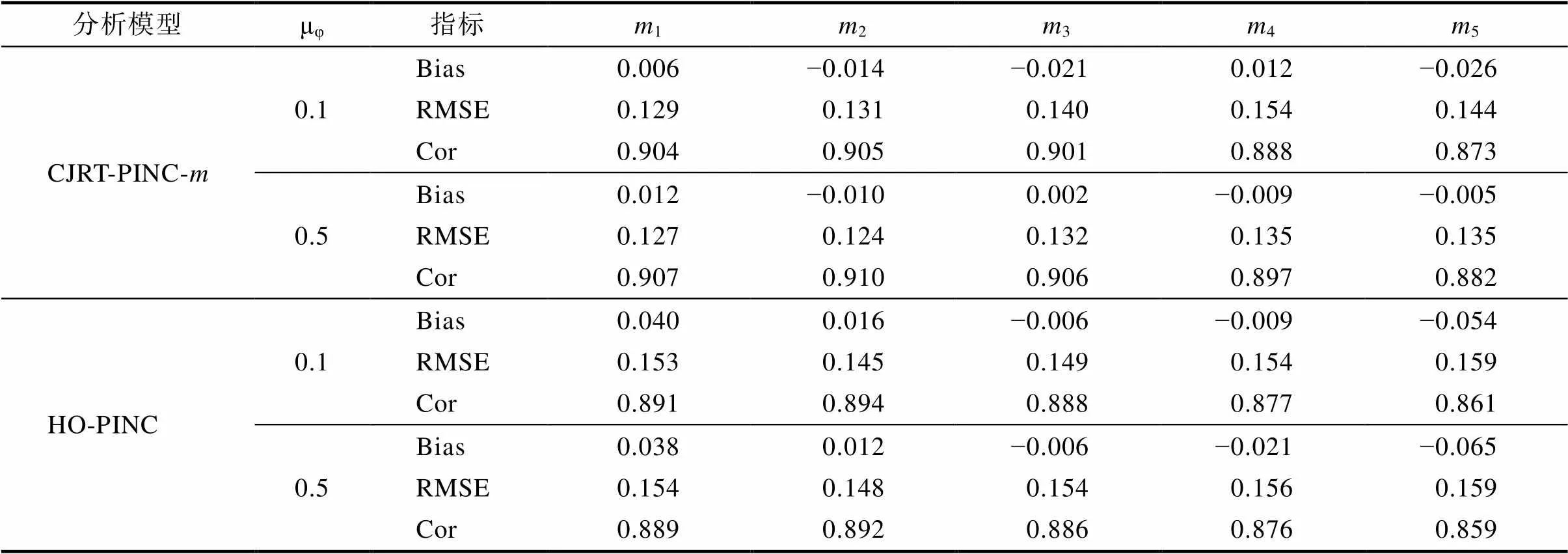
分析模型μφ指标m1m2m3m4m5 CJRT-PINC-m0.1Bias0.006−0.014−0.0210.012−0.026 RMSE0.1290.1310.1400.1540.144 Cor0.9040.9050.9010.8880.873 0.5Bias0.012−0.0100.002−0.009−0.005 RMSE0.1270.1240.1320.1350.135 Cor0.9070.9100.9060.8970.882 HO-PINC0.1Bias0.0400.016−0.006−0.009−0.054 RMSE0.1530.1450.1490.1540.159 Cor0.8910.8940.8880.8770.861 0.5Bias0.0380.012−0.006−0.021−0.065 RMSE0.1540.1480.1540.1560.159 Cor0.8890.8920.8860.8760.859

注: CJRT-PINC-= 基于属性的联合−交叉负载概率态输入, 噪音连接模型; HO-PINC = 高阶概率态输入, 噪音连接模型; μφ= 交叉负载均值;= 概率态属性; Bias = 所有被试的平均偏差; RMSE = 所有被试的平均均方根误差; Cor = 估计值与真值之间的相关系数。

表S3.5 研究2 (子研究2)中题目参数的返真性

表S3.6 研究2 (子研究2)中题目参数方差协方差矩阵和均值向量的返真性

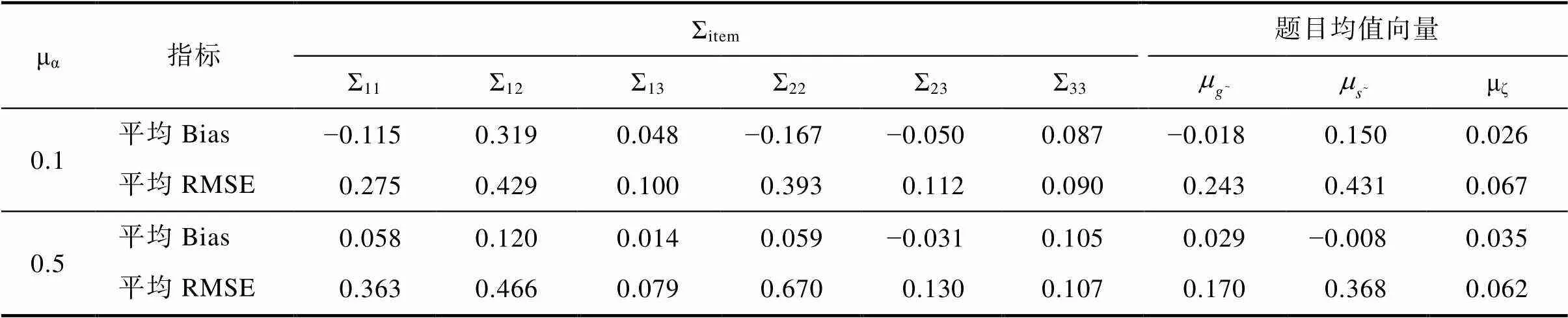
μα指标Σitem题目均值向量 Σ11Σ12Σ13Σ22Σ23Σ33μζ 0.1平均Bias−0.1150.3190.048−0.167−0.0500.087−0.0180.1500.026 平均RMSE0.2750.4290.1000.3930.1120.0900.2430.4310.067 0.5平均Bias0.0580.1200.0140.059−0.0310.1050.029−0.0080.035 平均RMSE0.3630.4660.0790.6700.1300.1070.1700.3680.062

表S4.1 研究3中被试参数的返真性

数据生成模型数据分析模型θτ BiasRMSECorBiasRMSECor JRT-PINCJRT-PINC0.000 0.4570.887−0.001 0.1200.951 CJRT-PINC-θ−0.002 0.4750.878−0.002 0.1810.885 CJRT-PINC-m−0.001 0.4750.877−0.003 0.1320.943 CJRT-PINC-θJRT-PINC0.007 0.4120.910−0.013 0.4960.600 CJRT-PINC-θ0.009 0.2860.959−0.016 0.1940.886 CJRT-PINC-m0.010 0.3020.954−0.016 0.3560.740 CJRT-PINC-mJRT-PINC0.003 0.4750.8790.008 0.1710.902 CJRT-PINC-θ0.008 0.4660.8840.004 0.1430.936 CJRT-PINC-m0.005 0.4560.8890.005 0.1430.937

表S4.2 研究3中属性参数的的平均Bias

数据生成模型数据分析模型m1m2m3m4m5 JRT-PINCJRT-PINC0.006 0.007 0.008 −0.008 −0.022 CJRT-PINC-θ0.005 0.005 0.007 −0.006 −0.023 CJRT-PINC-m0.015 0.011 0.010 −0.004 −0.028 CJRT-PINC-θJRT-PINC−0.017 −0.014 −0.019 −0.024 −0.026 CJRT-PINC-θ−0.016 −0.009 −0.018 −0.018 −0.017 CJRT-PINC-m0.016 0.0120.029 0.020 −0.038 CJRT-PINC-mJRT-PINC0.031 0.001 −0.020 0.002 −0.015 CJRT-PINC-θ0.026 0.009 −0.024 0.002 −0.020 CJRT-PINC-m0.033 0.011 −0.016 −0.001 −0.013

表S4.3 研究3中属性参数的的平均RMSE

数据生成模型数据分析模型m1m2m3m4m5 JRT-PINCJRT-PINC0.1260.1380.1420.1470.143 CJRT-PINC-θ0.1280.1400.1460.1480.145 CJRT-PINC-m0.1320.1430.1440.1510.147 CJRT-PINC-θJRT-PINC0.1160.1310.1390.1370.133 CJRT-PINC-θ0.0880.1030.1460.1090.103 CJRT-PINC-m0.1560.1420.1100.1300.150 CJRT-PINC-mJRT-PINC0.1390.1500.1510.1460.143 CJRT-PINC-θ0.1340.1490.1490.1420.141 CJRT-PINC-m0.1370.1430.1420.1390.136

表S4.4 研究3中属性参数的的Cor

数据生成模型数据分析模型m1m2m3m4m5 JRT-PINCJRT-PINC0.8990.8990.8950.8870.874 CJRT-PINC-θ0.8940.8940.8880.8800.866 CJRT-PINC-m0.8930.8940.8890.8790.865 CJRT-PINC-θJRT-PINC0.9170.9160.9130.9070.896 CJRT-PINC-θ0.9560.9550.9540.9530.949 CJRT-PINC-m0.9380.9450.9520.9500.937 CJRT-PINC-mJRT-PINC0.8950.8930.8910.8810.866 CJRT-PINC-θ0.9010.9000.8970.8880.873 CJRT-PINC-m0.9030.9030.9010.8920.877

表S5.1 研究3实证数据Q矩阵

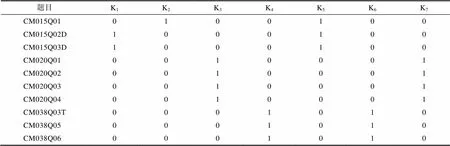
题目K1K2K3K4K5K6K7 CM015Q010100100 CM015Q02D1000100 CM015Q03D1000100 CM020Q010010001 CM020Q020010001 CM020Q030010001 CM020Q040010001 CM038Q03T0001010 CM038Q050001010 CM038Q060001010

图S5.1 实证数据中模型加工速度参数估计值散点图

注: y轴对应模型比x轴对应模式的估计值更大, 则散点趋势高于对角线表明; 反之, 散点趋势低于对角线。

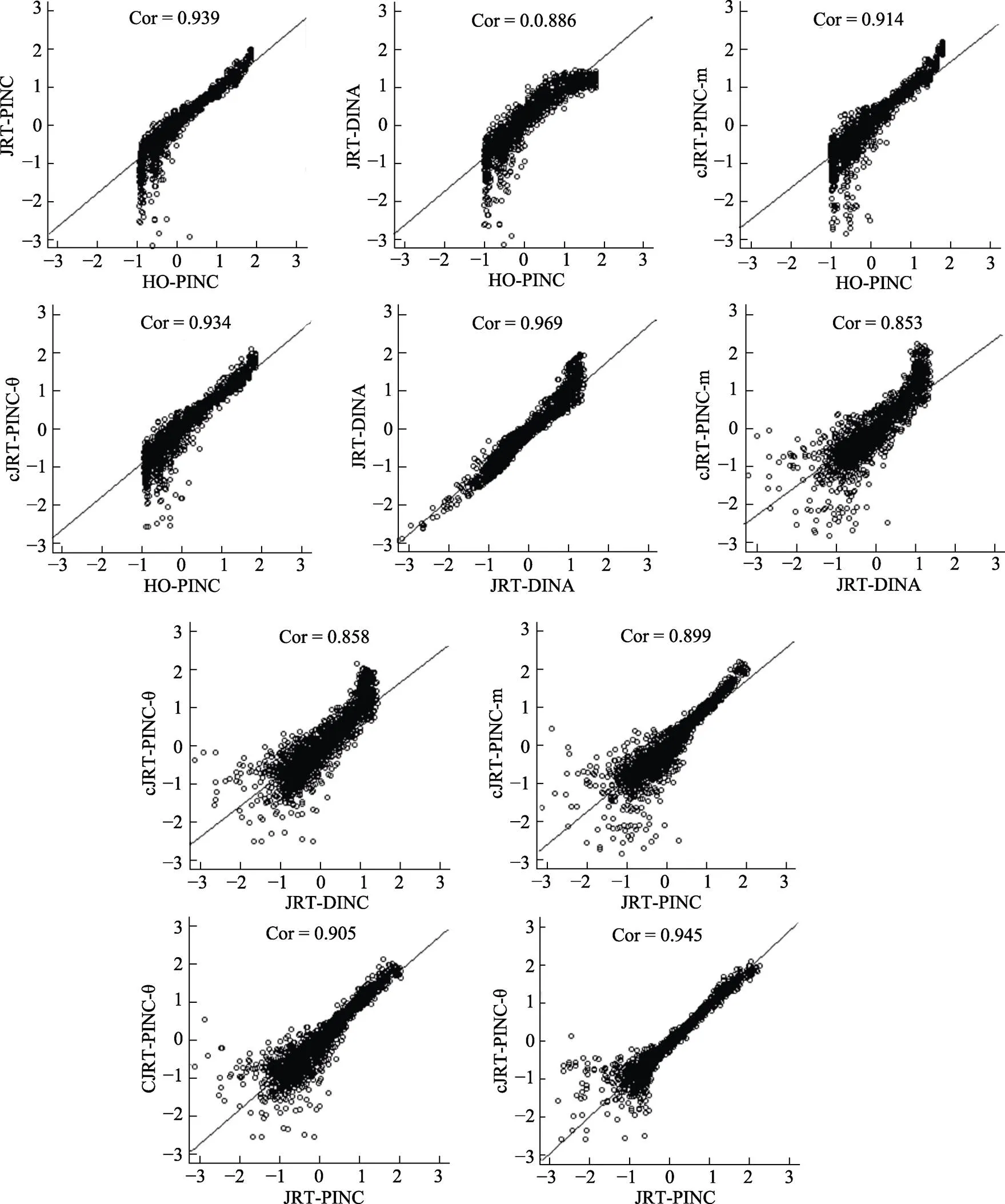
图S5.2 实证数据中模型潜在能力参数估计值散点图

注: y轴对应模型比x轴对应模式的估计值更大, 则散点趋势高于对角线表明; 反之, 散点趋势低于对角线。

Joint cognitive diagnostic modeling for probabilistic attributes incorporating item responses and response times

TIAN Yashu, ZHAN Peida, WANG Lijun

(School of Psychology, Zhejiang Normal University; Intelligent Laboratory of Child and Adolescent Mental Health and Crisis Intervention of Zhejiang Province; Key Laboratory of Intelligent Education Technology and Application of Zhejiang Province, Jinhua 321004, China)

Compared with the conventional CDM with deterministic or binary attributes, the CDM with probabilistic attributes (probabilistic-CDM) can achieve a more refined diagnosis of attribute mastery status, which helps distinguish individual differences between students and provides more reference information for teacher feedback. However, existing probabilistic CDMs can only analyze a single modal of data—item response accuracy (RA), ignoring other modals of data such as item response times (RTs). RTs reflect the cognitive processing speed of the participant. With the popularity of computerized testing, recording RT data has become routine. However, how to use RTs in probabilistic CDM to further improve parameter estimation accuracy and enrich the diagnostic feedback information is still an unsolved methodological problem. To this end, the current study proposes three joint probabilistic CDMs based on the joint-hierarchical and joint-cross-loading cognitive diagnostic modeling approaches.

First, based on joint-hierarchical modeling, the joint-hierarchical probabilistic CDM (JRT-PINC) was proposed in Study 1, which achieved the purpose of using RT to improve diagnostic accuracy. A simulation study was conducted to investigate the psychometric performance of the JRT-PINC under various simulated testing conditions, in which three independent variables, including sample size, test length, and the correlation between person parameters, were manipulated. Second, two joint-cross-loading probabilistic CDMs (CJRT- PINC-θ and CJRT-PINC-) were proposed based on the joint-cross-loading modeling. In contrast to the JRT-PINC model, two CJRT-PINC models directly used RTs to provide information for latent abilities or attributes by introducing item-level cross-loading parameters. Two CJRT-PINC models released some conditional independence assumptions in JRT-PINC, increasing their application scope. Two simulation studies were conducted to explore their performance under different simulated conditions with different degrees of cross-loading. Third, Study 3 aims to explore the relative merits of the JRT-PINC and two CJRT-PINC models, that is, the necessity of considering cross-loading in the joint analysis of RA and RT. Finally, an empirical example was conducted to illustrate the practical applicability of the proposed models and to compare them with existing CDMs (e.g., CDMs with deterministic attributes).

The simulation results mainly indicated that: (1) all three proposed models can be well recovered under different simulated conditions; (2) CJRT-PINC-θ makes fuller use of the information contained in RTs and thus improves the accuracy of the parameter estimation of the core constructs (e.g., latent ability and attributes) than CJRT-PINC-; and (3) the adverse effects of ignoring the possible cross-loadings are more severe than redundantly considering them. The results of the empirical example indicated that: (1) probabilistic attributes provide more refined feedback on participants' mastery of attributes than deterministic attributes; and (2) two CJRT-PINC models fit this data better than the JRT-PINC model.

Overall, this paper introduced RTs in probabilistic CDM for the first time and proposed three joint probabilistic CDMs based on two joint cognitive diagnostic modeling approaches. This study enriched the scope of application of probabilistic CDMS and provided methodological guidance for further refined and comprehensive diagnosis by jointly analyzing multi-modal data in technology-enhanced assessment systems.

cognitive diagnosis, probabilistic attribute, item response time, joint modeling framework, cross loading

B841

2022-08-30

* 国家自然科学基金青年基金项目(31900795)资助。

詹沛达, E-mail: pdzhan@gmail.com; 王立君, E-mail: frankwlj@163.com