原子氧作用下聚酰亚胺薄膜剥蚀形貌仿真方法
焦子龙,乔世英,姜海富,姜利祥,刘宇明,徐焱林,李 涛
(1.可靠性与环境工程技术重点实验室;2.北京卫星环境工程研究所:北京 100094;3.中国航天科技集团有限公司,北京 100048)
0 引言
聚酰亚胺(PI)是性能优异的航天器用聚合物材料 ,广泛应用于热控材料[1-2]、柔性太阳电池基板和电路系统绝缘材料[3]等,作为帆面材料在太阳帆[4-5]和离轨帆[6]等新型空间应用方面也逐步得到重视。然而,在低地球轨道(LEO)原子氧(AO)的剥蚀作用[7-9]下,PI 表面粗糙度增大[10]造成PI 薄膜力学性能退化,可能引起PI 薄膜撕裂[11]。粗糙度增大使Kapton/Al 薄膜太阳吸收比增加,影响航天器的热平衡[12]。粗糙度增大还可以使卫星光谱产生红化效应,进而影响地基观测在轨人造目标时对目标反射光谱的解析[13]。此外,对薄膜粗糙度变化所引起的透过率变化分析还是某些在轨原位测量AO通量技术的关键[14]。
目前对PI 薄膜剥蚀形貌的变化规律研究仍较少。Banks 等最早对PI 薄膜剥蚀形貌进行了研究[15-19],仿真分析了在轨和地面热等离子体试验条件下AO 剥蚀深度标准差的变化规律,仿真设置的AO 累积通量为4.0×1020atom·cm-2。结果发现,在轨条件下该标准差随着AO 累积通量增加而增大,但并非线性变化,且地面热等离子体试验条件下产生的剥蚀形貌远不如在轨条件下的形貌粗糙[16]。Allegri 等基于LDEF 及Mir 在轨暴露试验获得的Kapton 薄膜透过率数据,结合仿真数据(AO 累积通量为5.3×1020atom·cm-2)发现,随着AO 通量增加,Kapton 薄膜粗糙度先是快速增大,而后逐渐稳定在250 nm 左右[20]。有些研究人员在地面试验中也发现粗糙度随暴露累积通量增加而增大,但未能进一步深入研究其变化规律[12]。
因此,针对PI 薄膜表面粗糙度变化规律问题,本文改进了用于AO 掏蚀效应分析的常规计算方法,提出基于粒子运动路径的局部网格边界相交判断的计算方法,并将其用于AO 作用下PI 薄膜剥蚀形貌变化模拟,研究了不同AO 束流参数下的PI 薄膜表面形貌变化,对结果进行了分析讨论。
1 模拟方法
Banks 等提出了基于蒙特卡罗法的AO 与PI薄膜相互作用计算方法,并首次将其用于带有保护涂层的PI 薄膜掏蚀形貌计算[15-19]。该方法的基本原理为:以1 个模拟粒子代表大量AO。采用二维模型,计算域以矩形网格表示。在计算域边界随机布置模拟粒子,速度以麦克斯韦速度分布抽样。然后观察模拟粒子前进轨迹上与其相交的边界和网格,通过随机抽样判断模拟粒子是否发生反应:如发生反应,则标记相应网格为已剥蚀,该粒子模拟终止,开始下一个粒子的模拟。如不发生反应,表明模拟粒子发生镜面反射或漫反射,其反应概率发生相应改变,继续追踪粒子的运动轨迹,重复上述相交等过程计算;若粒子反射一定次数后仍未能发生反应,为提高计算效率,令该粒子模拟终止。
粒子与网格边界相交计算是计算量最大的部分。为了加快计算速度,高劭伦等[21]、李涛等[22-23]、Liu 等[24]、Yang 等[25]采用四叉树、双链表等技术对粒子与网格边界相交计算方法进行改进。但是上述改进中寻找相交的网格边界是在整个计算域进行的,计算量仍较大。
本文提出基于粒子运动路径的局部网格边界相交判断的计算方法,如图1 所示。图1(a)为粒子在计算域中运动的示意:计算域为长方形区域,宽度方向为x方向(向右为+x方向),厚度方向为y方向(向下为+y方向)。在模拟边界处随机产生模拟粒子的位置和速度。由于网格为长方形或正方形,所以很容易计算得到其所在网格。然后,根据模拟粒子运动轨迹信息和网格顶点坐标计算得到相交边界。若相交边界所属网格已被剥蚀,则模拟粒子保持原速度继续运动。若所属网格为PI 材料,判断模拟粒子是否与其发生反应,如不发生反应,粒子将按照镜面反射或漫反射规律从边界反射,继续运动。该计算方法将AO 的运动计算仅局限于当前网格,避免在整个计算域进行搜索判断,与传统计算方法相比有望显著减小计算量,提高计算效率。

图1 局部网格边界相交判断的计算方法Fig.1 Calculation method for determining local grid boundary intersections

判断上述t值中的最小正值,记为tmin。若tmin=t1,则相交边界为①,粒子运动至当前网格左侧网格;若tmin=t2,则相交边界为②,粒子运动至当前网格右侧网格;若tmin=t3,则相交边界为③,粒子运动至当前网格上方网格;若tmin=t4,则相交边界为④,粒子运动至当前网格下方网格。
计算机模拟中会出现如图2 所示边界现象,即模拟区域左右边界处剥蚀不完全。这是由于仿真计算时左右边界处AO 只能来自一侧,使得剥蚀出现不符合实际物理规律的结果。为此,须采用周期性边界处理方法,即以x方向模拟区域尺寸Lx为周期,将x坐标向下取整数,得到新坐标x′,

图2 仿真计算中与实际不符的边界现象示意Fig.2 Schematic diagram of boundary effect in simulation not matching reality
而y方向坐标及其速度保持不变。
由于该方法为统计模拟方法,需要进行多次统计抽样以减小误差。一般而言,统计误差与模拟次数N的1/2 次方成反比[24],即,过度增大模拟次数并不能有效减小统计误差。本文将模拟次数设置为50 次。
2 计算方法验证
采用文献[15]中带有保护涂层的Kapton 薄膜AO 掏蚀效应试验结果对本文提出的计算方法进行验证。由于Kapton 薄膜的保护涂层存在裂纹等缺陷,当AO 穿过缺陷作用于底层材料时形成掏蚀。为模拟保护涂层,将计算区域顶部一部分边界设置为不与AO 发生反应。AO 与Kapton 材料相互作用的参数取自文献[15],如表1 所示。计算区域设置为深50 μm、宽50 μm,缺陷宽度为2 μm,AO 累积通量为5.77×1021atom·cm-2。
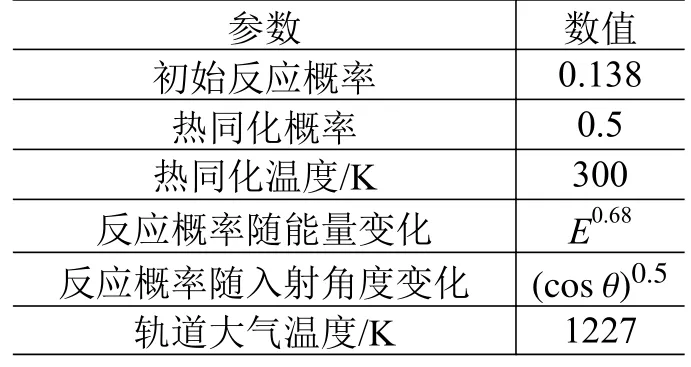
表1 仿真计算参数设置Table 1 Parameter settings for simulation calculation
计算得到的掏蚀形貌如图3 所示,图3(a)为本文计算结果,图3(b)为本文计算结果与文献[15]中的试验结果进行对比,图中红色曲线为文献[15]结果,黑色曲线为本文仿真结果。本文得到的掏蚀深度为36.5 μm,文献[15]的结果为38.0 μm。两者相对误差为3.94%,表明利用本文算法对AO 与Kapton 的相互作用进行仿真的结果与试验结果接近。
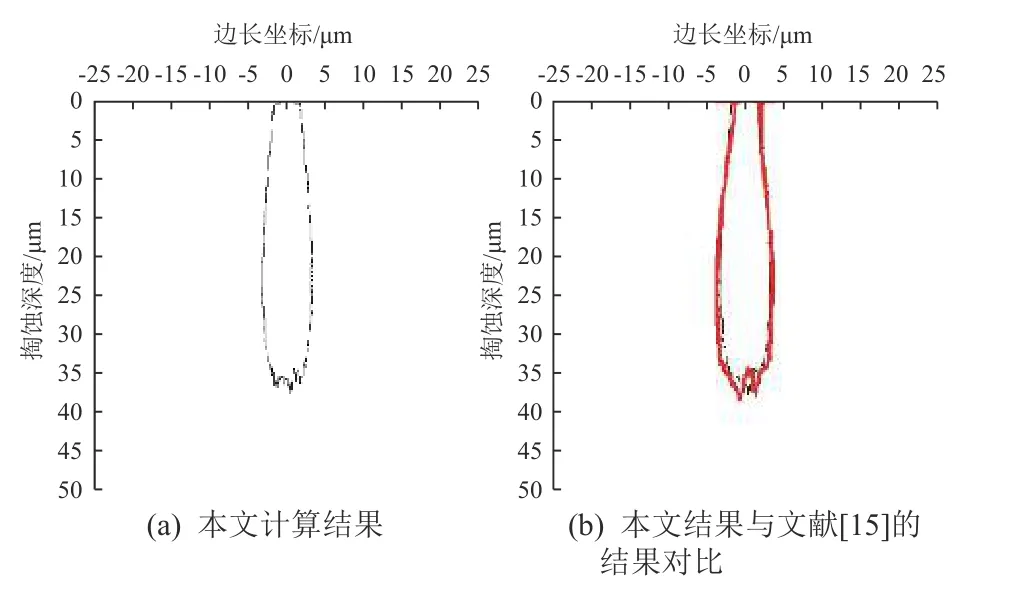
图3 带有保护涂层的Kapton 掏蚀深度本文计算结果与文献[15]试验结果对比Fig.3 Comparison of undercutting depth of protected Kapton film of calculated result in this work with experimental result in Ref.[15]
3 表面剥蚀形貌仿真分析与讨论
3.1 仿真结果
针对表面形貌变化仿真,设置初始为光滑表面、边长为100 μm 的正方形为计算区域。仿真的AO 累积通量为1.0×1021atom·cm-2,通量的仿真步长为2.0×1019atom·cm-2,共仿真50 步,得到的典型形貌变化如图4 所示。为对比方便,将多个形貌叠加在了一起,图中尖刺状黑色线条表示材料本体。对 应 累 积 通 量 分 别 为:2.0×1019atom·cm-2、2.0×1020atom·cm-2、4.0×1020atom·cm-2、6.0×1020atom·cm-2、8.0×1020atom·cm-2和 1.0×1021atom·cm-2。
从图4 可以看出,AO 作用导致了材料不断被剥蚀,厚度逐渐减小;同时,形貌也有明显变化,主要体现在峰和谷形貌的变化。对比对应位置的峰的变化,发现其逐渐变高并且变尖,而后逐渐变矮直至消失;谷的变化则是逐渐变深和变宽,而后又逐渐变浅和变细。仿真获得的形貌与图5 中Shimamura等在地面试验中获得的典型形貌[11]极为相似。

图5 AO 地面试验中Kapton 薄膜截面典型形貌[11]Fig.5 Morphology of Kapton film under AO in ground experiment[11]
统计得到的剥蚀深度随AO 累积通量的变化如图6 所示。从图中可以看出,虽然理论上航天器在轨运行速度(简称“轨道速度”)越快,AO 具有的相对平均动能越高,剥蚀深度越大;但是由于不同轨道速度下AO 相对能量变化不大,且根据表1 中反应概率和能量的关系,可知不同轨道速度下剥蚀深度相差不大。若考虑模拟误差的影响,可忽略不计。
统计得到了PI 薄膜表面轮廓距离平均剥蚀深度的算术平均偏差和标准差随AO 累积通量的变化,如图7 所示。

图7 PI 薄膜表面轮廓距离平均剥蚀深度随AO 累积通量的变化Fig.7 Variation of surface profile relative to the average erosion depth of PI film with AO fluence
图中还给出了轨道速度对仿真结果的影响,模拟设定轨道速度为7.8 km·s-1、7.7 km·s-1、7.6 km·s-1、7.5 km·s-1和7.4 km·s-1。从图中可以看出:不同轨道速度下,表面轮廓距离平均剥蚀深度变化规律基本相同;AO 累积通量较小时,表面轮廓距离平均剥蚀深度的算术平均偏差和标准差迅速增大。随着AO 累积通量增大,两者变化逐渐平缓。轨道速度越高,两者数值越大,但相差不大。这主要是因为AO 能量相差不大,因而与PI 反应特性基本相同。算术平均偏差和标准差变化趋势相同。比较图7(a)与图7(b)的数值,发现两者对应AO 累积通量下的比例固定,约为1.25。这说明PI 薄膜的表面形貌特征基本未变,只是表面峰/谷数值变大。
将上述计算结果与文献[16]中模拟轨道速度7.8 km·s-1的算术平均偏差结果进行了比较,结果如图8 所示。可以看出,AO 累积通量大于等于8.0×1019atom·cm-2时符合较好。

图8 本文算术平均偏差与文献[16]对比Fig.8 Comparison between the arithmetic mean deviation in this paper and Ref.[16]
针对轨道速度为7.8 km·s-1的PI 薄膜形貌参数计算结果进行其与AO 累积通量关系拟合,结果如表2 所示。

表2 PI 薄膜形貌参数与AO 累积通量关系拟合结果Table 2 Fitting results of PI film morphology parameters with AO fluence
根据拟合结果可以看出,形貌参数以AO 累积通量的0.253 次幂规律增大。
3.2 讨论
目前对AO 剥蚀形貌微观机理和形貌参数长期变化趋势的研究仍存在不足。本文结果是基于文献中AO 与PI 材料作用参数(如反应概率及其随入射角度和能量的变化、热同化概率等)计算获得的,但上述参数是通过掏蚀形貌计算拟合在轨实验数据所得,其合理性尚需进一步分析。
本研究中采用矩形网格表示材料单元的合理性仍有待进一步研究,也有必要探讨采用其他几何结构,如三角网格等进行剥蚀形貌计算分析——三角形网格可能更适合表示起伏的峰谷形貌,但编程实施难度会显著增加。另外,有必要进行三维形貌的计算分析和试验表征,因为其可对二维形貌计算中采用的作用参数进行验证。
目前系统的剥蚀形貌定量研究仍较少,无法对仿真结果进行深入对比验证。因此表面形貌的测量和表征试验对于AO 剥蚀形貌研究极为重要。
4 结束语
为进一步研究PI 薄膜在AO 束流作用下的表面剥蚀形貌,参考现有蒙特卡罗掏蚀形貌仿真方法,提出了一种基于局部网格边界相交判断的方法,并应用周期性边界处理方法获得符合实际物理规律的表面形貌。采用本文方法仿真了已有的掏蚀形貌算例,计算结果与文献[15]中的试验结果相差小于4%,证明本文计算方法能够正确描述AO 与PI 材料的相互作用。
采用剥蚀形貌与平均剥蚀深度的算术平均偏差和标准差作为材料形貌特征的描述参数。结果发现,算术平均偏差和标准差均随着AO 累积通量增大而以0.253 次幂律增大;标准差和算术平均偏差的比值随AO 累积通量增大基本保持不变,说明表面形貌特征在AO 作用下基本不变,只是表面峰值和谷值增大。此外,不同轨道速度条件下表面剥蚀形貌差异不大。
本文的仿真分析方法和计算结果将有助于更好地理解AO 作用下航天器用聚合物表面剥蚀形貌形成机理,为PI 等航天用聚合物薄膜材料更好的空间应用提供保障。

