钻井船插拔桩对临近桩靴承载力的拟静力模拟研究
唐德佳,曹添铭,梁 超,陈广思
(1.中国海洋石油集团有限公司物装采购中心,天津 300457;2.天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
近年来,我国广泛采用自升式钻井平台进行海上油田开采。自升式平台由上层船体平台、桩腿、桩靴和升降装置等部分组成。平台作业过程中,需经拖航到达预定位置,并进行插桩作业,将大直径桩靴压入海底泥面,平台作业完成后,将桩靴上拔后离开,在原位置会留下桩坑脚印。钻井船的插拔桩过程强烈挤压周围土体,进而影响临近井口平台的稳定性,如图1所示。
图1 钻井平台对临近平台的影响Fig.1 The influence of the drilling platform on adjacent platform
针对平台桩靴承载力及插桩过程阻力的研究,早期学者根据传统地基承载力理论进行预测,主要基于PRANDTL或TERZAGHI提出的条形基础地基承载力解[1-2],SNAME规范[3]提出了考虑土体回流的计算公式。HOSSAIN等[4-6]通过开展一系列的离心模型试验对桩靴基础的贯入问题进行了研究,MARTIN等[7]和CASSIDY等[8]通过模型试验得到桩靴基础在竖向荷载V、水平荷载H、弯矩荷载M耦合作用下的承载力以及VHM荷载空间承载力包络面。数值模拟方面,LIU等[9]采用基于网格重划分小应变插值技术的RITSS(Remeshing and Interpolation Technique with Small Strain Approach)方法对上层砂土下层粘土地基进行了分析,研究了插桩阻力并预测了穿刺的易发位置。LI等[10]、MAO等[11]利用网格自适应技术ALE(Arbitrary Lagrangian-Eulerian),对桩靴插桩过程进行了分析。THO等[12-13]利用耦合欧拉-拉格朗日CEL法(Coupled Eulerian-Lagrangian)引入到了桩靴在粘土层中的贯入阻力预测,计算结果与现有离心模型试验[14]吻合较好。安永宁[15]采用有限元方法计算地基承载力并与各经典公式和规范方法对比,验证有限元方法的便利性和有效性。
在实际工程中,已在位平台会有钻井船临时停靠进行钻修井作业,钻井船桩靴的插拔过程对已在位的临近桩基础造成不利影响。已有离心机试验[14,16-17]表明桩靴插入与拔出引起周边土体应力场发生变化,进而影响已在位的桩基础,其中影响承载力、桩身弯矩、桩身变形的关键因素包括桩靴尺寸、贯入深度、桩靴与临近桩基础间距。针对以上不同因素的影响程度,许多学者借助数值模拟方法开展桩靴插拔对临近桩基础的影响研究,其中CEL[18-20]方法较为常见,也取得了许多有价值的研究成果。
目前的研究成果多集中在对桩靴插拔本身的研究或其对临近钢管桩基础的影响,但工程中许多已在位平台采用桩靴基础,钻井船桩靴插拔过程对已在位桩靴基础的影响亦不可忽视,针对临近桩靴影响的研究,刘润等[21-22]开展了砂土中模型试验,但尚未有学者采用数值模拟方法对不同因素的影响程度开展规律性研究。本文基于岩土工程软件PLAXIS,开展桩靴插拔对临近平台桩靴承载力影响进行研究,旨在揭示已在位桩靴承载力受桩靴插拔的影响。
1 简化的拟静力方法
1.1 拟静力模拟方法的建立
桩靴插拔过程的模拟涉及大变形问题,常规有限元模拟方法易出现网格畸变,动力算法因无法准确模拟桩靴插拔后土体强度的降低,在研究桩靴插拔引起的临近结构物承载力变化方面存在缺陷。因此建立合理的拟静力方法成为解决这一问题的重要途径。观察桩靴插拔的模型试验过程,研究桩靴对土体的扰动范围和土体强度的下降规律是建立桩靴插拔过程拟静力模拟的关键。
根据SICILIANO等[16]和XIE[14]离心机模型试验以及KELLEZI等[23]数值模拟研究可知,桩靴插拔对土体的扰动区域,在水平方向约为桩靴以外1倍桩靴直径D范围内。张海洋等[24-25]的桩靴插拔模型试验表明,插拔桩过程对周边土体的影响主要包括两个方面:一是对周围土体产生卸荷作用,土体应力状态改变;二是导致周围土体强度的下降,且土体强度的下降程度随距桩靴脚印中心距离及埋深的增加而逐渐减弱。刘润等[21]给出了桩靴插拔后周边土体强度随间距的变化,如图2-a中曲线所示。以此为基础,将桩靴插拔的动态作用过程简化为对周边土体扰动的拟静力模拟方法,即将桩靴插拔后的地基分为3个区域:(1)桩靴脚印区;(2)影响区;(3)无影响区,如图2-b所示。
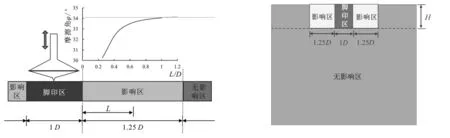
2-a 摩擦角-距离规律 2-b 整体分区图2 土体分区示意图Fig.2 Soil model area division
图2中脚印区为桩靴插拔后在土体中遗留的坑洼孔穴,数值计算中难以模拟孔穴内的真实状态,将脚印区简化为与桩靴直径D相同的圆柱体区域,高度等于桩靴插深H,土体填满孔穴,对脚印区原土体参数进行折减,形成等效土体参数,模拟孔穴对整个脚印区土体的影响;影响区为插拔桩作业引起的周围受扰动土体区域,依据模型试验结果,圆环影响区径向范围距脚印区边缘1.25D,深度范围等于桩靴插深H,此部分可按照试验确定的土体强度折减规律对影响区土体进行折减计算,模拟插拔对土体的影响;其余部分土体为无影响区。
1.2 拟静力分析模型的建立
按照上述分区方法建立数值模型,采用PLAXIS软件对张海洋等[24-25]的离心机试验结果进行模拟,计算砂土中桩靴插拔桩对临近桩基础竖向承载力的影响。计算模型如图3所示,图3中D为桩靴直径,H为桩靴贯入深度,L为临近桩到脚印区外边缘最小间距。土体采用摩尔-库伦本构模型,对各区域设置相应的模型材料属性参数,其中脚印区土体,降低原有土体强度、压缩模量、容重等参数,模拟桩靴贯入-拔出动作结束后的孔穴扰动土体,将影响区内的土体细分若干环形区域,各环形区土体结合土体强度随距离降低规律[21]按比例折减,临近桩采用梁单元模拟,各计算参数见表1。
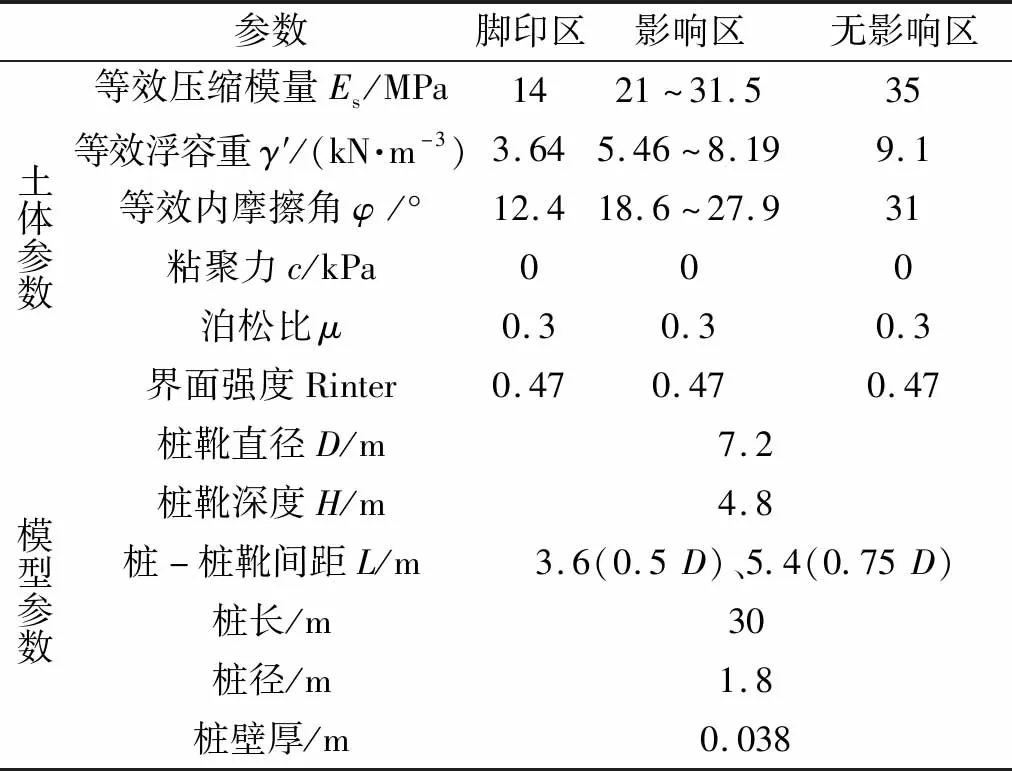
表1 计算参数Tab.1 Soil material parameter
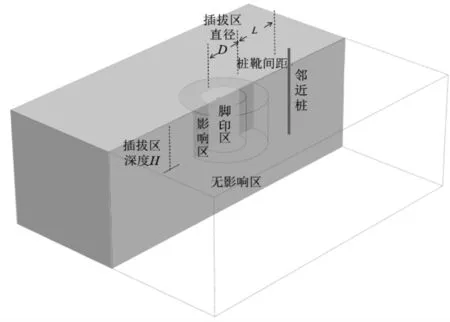
图3 PLAXIS中临近桩承载力模型Fig.3 Bearing capacity model of adjacent piles in PLAXIS
1.3 拟静力方法计算结果的验证
分别计算土体无折减情况下单桩以及当桩基础位于距桩靴边缘0.75D与0.5D时的桩基竖向承载力,桩顶施加位移s=0.1 m。对比计算结果可得到桩靴插拔导致的桩基承载力下降程度,桩基的载荷-沉降曲线如图4所示,计算的单桩承载力折减率结果如表2所示。

表2 竖向承载力折减率η对比Tab.2 Comparison of vertical bearing capacity reduction rate η

图4 单桩竖向沉降-载荷曲线Fig.4 Vertical settlement-load curve of single pile
根据表2可知,采用PLAXIS计算的承载力折减率结果与张海洋等[24-25]的离心机试验吻合较好,说明建立的简化拟静力方法具有可行性。
2 桩靴插拔对临近桩靴的影响
2.1 数值分析模型的建立
采用前述方法,建立模拟桩靴插拔影响的简化拟静力分析模型,如图5所示,图5中D为桩靴直径,H为桩靴贯入深度,d为已在位临近桩靴直径,h为已在位桩靴目标贯入深度,L为2个临近桩靴外边缘最小间距。各区域材料参数如表3所示。
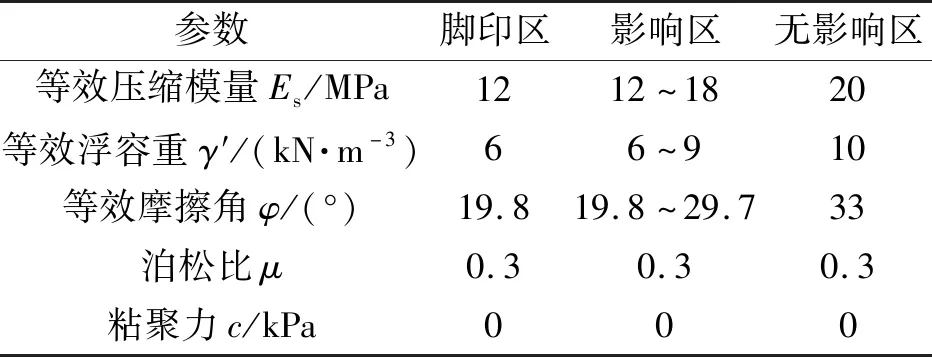
表3 材料参数Tab.3 Material parameter
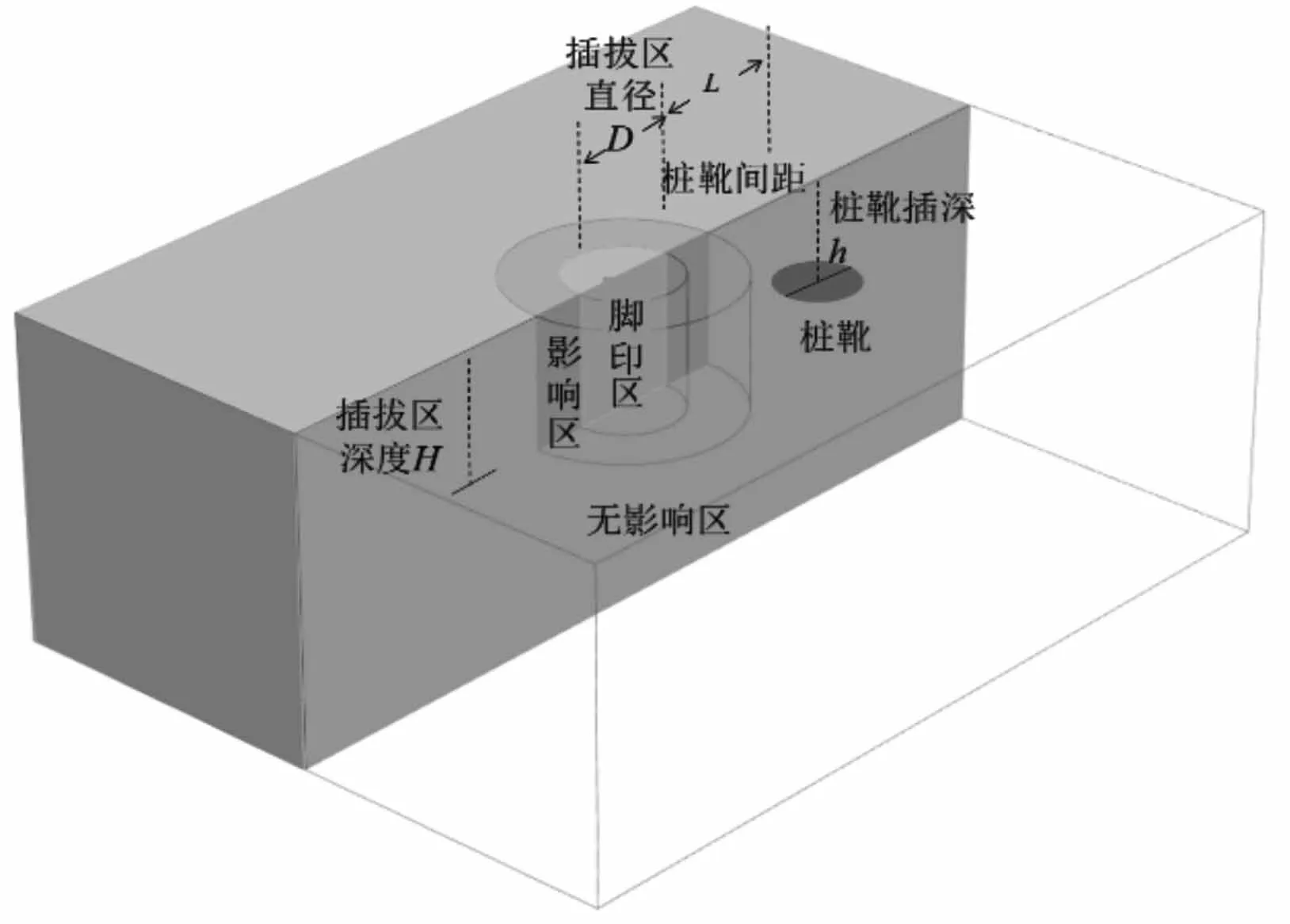
图5 模型图Fig.5 Finite element model diagram
本次研究重点关注桩靴承载力发挥,不考虑桩靴本身的结构变形,为此在计算过程中将桩靴材料弹性模量设置足够大,近似模拟为刚体以提升模型计算效率,同时考虑桩靴贯入对土体孔穴形状影响主要为桩靴自身最大面积截面的形状,将桩靴简化为圆形平板,直径为桩靴面积最大截面位置的直径。模型中土体和桩靴均采用四面体单元,在变形和应力较为敏感的脚印区和影响区网格进行加密以提升计算精度,模型如图6所示。
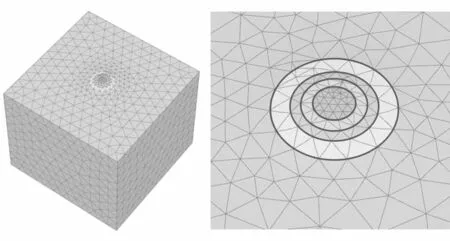
6-a 整体网格 6-b 脚印区局部网格图6 模型网格Fig.6 Model mesh
2.2 拟静力计算方法
拟静力计算方法主要将桩靴贯入—拔出过程对土体的扰动由动力简化为静力算法,并将扰动前的桩靴承载力和扰动后的承载力进行对比,量化承载力的影响程度。计算总体分为两个模型,包含土体未扰动计算模型和土体扰动计算模型。其中土体未扰动模型计算步骤为:
(1)初始地应力平衡分析。用于计算土体初始应力场。
(2)桩靴承载力计算分析。给予已在位临近桩靴竖向位移模拟贯入,得到桩靴贯入阻力与贯入位移曲线,得到在目标贯入深度h时的桩靴承载力。
土体扰动模型分析步骤:
(1)初始地应力平衡分析。用于计算土体初始应力场。
(2)卸荷分析。此步骤模拟桩靴贯入—拔出对土体的扰动,采用表3所示的方法,对脚印区、影响区进行土体参数折减,模拟孔穴的影响。
(3)桩靴承载力分析。对已在位桩靴进行下压至目标h深度,得到桩靴贯入阻力和贯入位移关系,分析得到已在位桩靴的承载力,并与土体未扰动模型计算结果进行比较,得到承载力折减规律。
根据以上步骤设计了6个组次的计算工况,如表4所示。
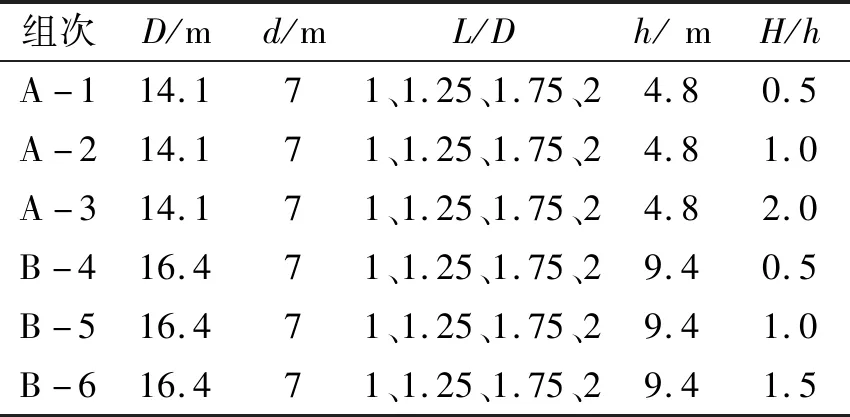
表4 计算工况Tab.4 Calculation condition
2.3 结果分析
以表4中B-5组次L/D=1的计算结果为例,给出了桩靴贯入阻力-位移曲线,如图7所示。
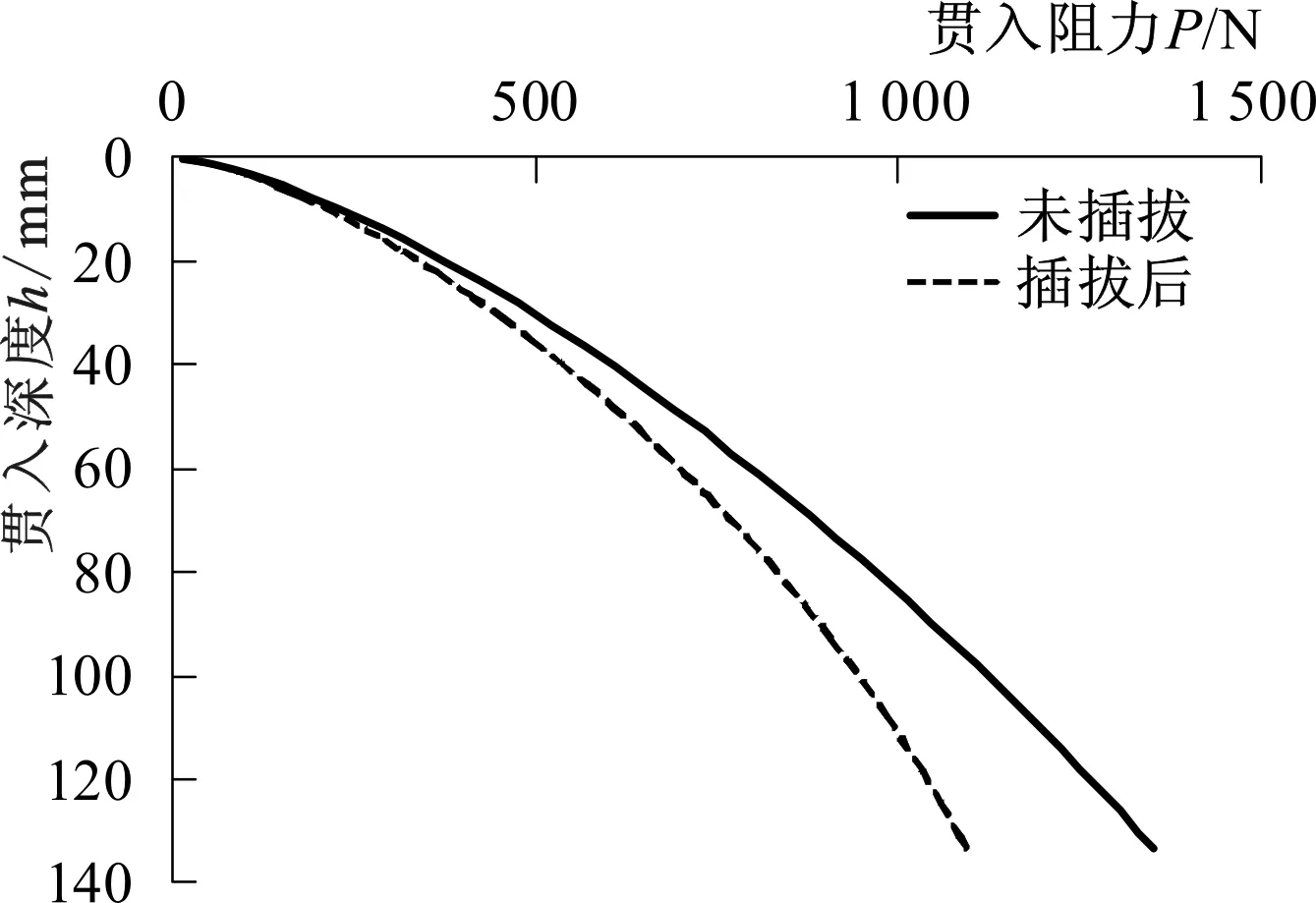
图7 贯入阻力-贯入深度曲线Fig.7 Penetration resistance-displacement curve
图7的结果显示,在相同位移条件下,桩靴插拔过程对已在位桩靴的承载力影响显著。为了量化其影响程度,定义桩靴承载力折减率为η,可按照下式计算
(1)
式中:P0为桩靴插拔前已在位桩靴承载力;P1为桩靴插拔后已在位桩靴承载力。
利用式(1)将表4中计算工况结果进行汇总,得到不同间距L/D条件下临近桩靴在目标贯入深度h时的桩靴承载力折减率,结果绘制如图8、图9所示。

8-a A-1、A-2、A-3组 8-b B-4、B-5、B-6组图8 折减率η与相对贯入深度H/h关系Fig.8 The relationship between η and the relative depth H/h
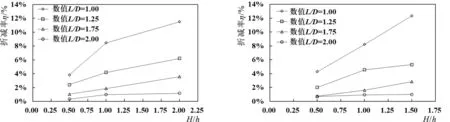
9-a A-1、A-2、A-3组 9-b B-4、B-5、B-6组图9 折减率η与相对间距L/D关系Fig.9 The relationship between η and the relative spacing L/D
通过分析强度折减率η与相对间距L/D关系可知,折减率η随相对贯入深度H/h的增加而增大,即桩靴贯入深度越小,桩靴承载力的影响程度越小;折减率η随两桩靴的相对间距L/D的增大而减小,即桩靴插拔位置距已在位桩靴越远,桩靴承载力的影响程度越小,相对间距L/D超过2.0时,折减率η小于1%,影响可忽略不计。
3 土体参数影响分析
3.1 土体初始强度的影响
以桩靴D=7 m、H=9.4 m、桩靴间距L/D=1的算例分析初始土体强度参数的影响,土体选取为砂土,采用内摩擦角φ为25°、30°、35°、40°四种工况,其他参数均相同。经计算得到不同摩擦角下桩靴承载力折减率变化规律如表5所示。

表5 不同摩擦角的计算结果Tab.5 Calculation results of different friction angles
由表5中结果可知,在桩靴插拔的拟静力数值模拟方法中,土体内摩擦角为25°~40°时,桩靴承载力随土体内摩擦角增加,桩靴承载力折减率随内摩擦角增大。
3.2 脚印区折减率的影响
拟静力算法中桩靴插拔过程形成的土体孔穴采用土体参数折减模拟,忽略了实际桩靴插拔时土体的位移、卸荷、回流等过程,但其折减率无法如影响区中可以采用试验测得,因此其参数选取对于计算结果的影响存在不确定性,为此对脚印区折减率的影响开展分析。
分别计算桩靴脚印区土体参数降低率为0%、20%、40%、60%和80%时的桩靴承载力折减规律,土体影响区参数分别对应按比例设置,结果如图10及表6所示。刘润等[21-22]的模型试验曲线如图11所示。

表6 不同土体参数降低率对应承载力折减率Tab.6 Reduction rate of bearing capacity with different reducing rate of soil parameters

图10 不同土体参数降低率贯入阻力-贯入深度曲线Fig.10 Resistance-depth curve with different reducing rate of soil parameters

图11 模型试验中贯入阻力-贯入深度曲线Fig.11 Penetration resistance-displacement curve in the test
由表6结果可知,桩靴承载力折减率随桩靴脚印区土体参数降低率增加。对比图10和图11可知,当桩靴插拔脚印区降低率为40%时,其结果与刘润等[21-22]、张海洋等[24-25]的模型试验结果最为接近,因此拟静力算法中建议采用40%的脚印区强度折减率。
4 结论
本文针对钻井船桩靴插拔对临近桩靴承载力产生不利影响的问题,开展数值模拟研究,主要结论如下:
(1)基于PLAXIS软件建立了考虑土体参数折减的简化拟静力分析法,并采用已有试验结果验证了该方法的可靠性。
(2)桩靴承载力折减率η随相对贯入深度H/h的增加而增大,即桩靴贯入深度越小,桩靴承载力的影响程度越小;折减率η随两桩靴的相对间距L/D的增大而减小,即桩靴插拔位置距已在位桩靴越远,桩靴承载力的影响程度越小,相对间距L/D超过2.0时,折减率η小于1%。
(3)桩靴承载力折减率随桩靴脚印区土体参数降低率增加,砂土中桩靴脚印区土体强度的降低率宜取为40%。

