岩土体抗剪强度对抗滑桩内力分布规律影响研究

肖可洋

(江西省水投建设集团有限公司，江西 南昌 330000)

滑坡灾害是全球范围内广泛发育的一种地质灾害，由于其规模大、分布范围广和危害性大的特点，容易造成较大的社会影响。

抗滑桩由于施工简单，治理效果优越而被广泛使用在滑坡治理工程中。国内外许多学者针对抗滑桩的受力性能及治理效果展开了深入的研究。麦合木提江[1]基于Geo-studio软件研究了抗滑桩对滑带土受力的影响。结果表明，抗滑桩对于水文地质条件复杂的滑坡治理效果良好。平诗语等[2]基于FLAC 3D数值有限元研究了滑坡的演化模式对抗滑桩的加固桩位与嵌固深度的影响。结果表明，桩体的有效嵌固深度比与滑坡类型无关，桩的最有效加固桩位并不一定是最合理桩位。仉文岗等[3]基于可靠度理论研究了岩体参数空间变异性对抗滑桩受力的响应。结果表明，强度参数的空间变异性对边坡的失效概率及抗滑桩响应有显著影响，不考虑岩土体的空间变异性将导致边坡失效概率增大及低估抗滑桩的桩顶位移。刘孟瀚等[4]基于极限平衡原理研究了桩前溶洞对抗滑桩嵌固段稳定性的影响，并基于极限平衡法提出了桩前存在溶洞时嵌固段承载力验算方法。周德培等[5]采用理论分析手段研究了边坡工程中抗滑桩合理桩间距。结果表明，其他条件不变的情况下，桩间距随桩后土体内聚力和内摩擦角增大而增大，随桩后推力的增大而减小。韩爱民等[6]基于数值模拟研究了影响桩间土拱效应因素。结果表明，土的泊松比、剪胀角和桩土接触特征对土拱效应的影响最明显。张建勋等[7]采用数值模拟研究了土体性质、群桩以及桩土接触面性质等因素对土拱效应的影响。结果表明，桩间距是影响土拱效应的最主要因素。戴自航[8]基于理论分析研究了滑坡推力和桩前滑体抗力分布规律，并建立了相应的滑坡推力和土体抗力分布函数模型，为滑坡治理及抗滑桩的合理设计提供参考。

本文基于数值模拟，研究了岩土体抗剪强度参数对抗滑桩内力分布特征影响。

1 数值模型

1.1 模型建立

建立典型数值计算模型如图1所示。边坡坡角为15°。抗滑桩共前后两排，长度均为16 m，桩径为1 m，嵌固段长度为6～7 m，桩心距为4 m，前后两排桩排距也为4 m。在滑体后方施加40 kN/m的水平均布荷载模拟滑坡推力。共建立10根桩，前后各5根。

图1 有限元分析模型

1.2 计算参数

岩土体破坏准则采用摩尔-库伦本构，抗滑桩采用各向同性完全弹性本构，钢筋采用强化拉伸塑性应力-应变本构。岩土体及钢筋混凝土的物理力学参数见表1所示。

表1 材料物理力学参数值

2 计算结果与分析

2.1 内聚力影响

图2汇总得到桩顶位移随内聚力变化规律，结果表明，在其他条件不变的情况下，桩顶位移随内聚力的增大而减小，但随内聚力逐渐增大，位移减小速率越来越平缓。也即内聚力越小，滑坡推力越大，桩顶位移越大。

图2 桩顶位移随内聚力变化规律

图3汇总得到前排桩和后排桩桩身弯矩随桩长的变化规律。结果表明，其他条件相同的情况下，内聚力对桩身弯矩影响较小。两排桩弯矩最大的位置均出现在桩身11 m的位置。

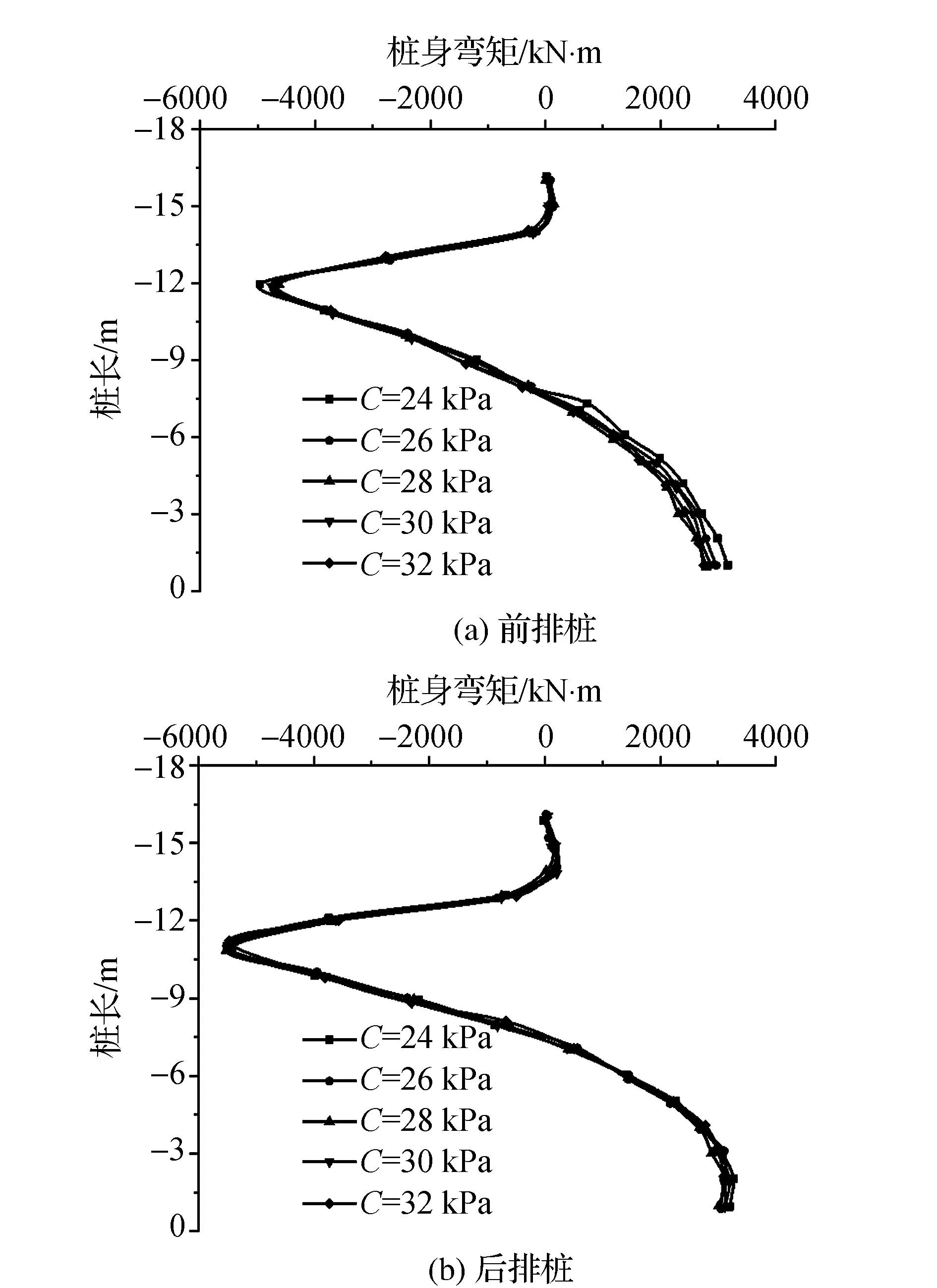
图3 桩身弯矩随桩长变化规律

进一步汇总得到桩身最大弯矩随内聚力变化规律见图4所示。结果表明，桩身最大弯矩随内聚力的增大而减小。随内聚力的增大，最大弯矩变化速率变平缓。对于后排桩而言，当内聚力分别为24 kPa、26 kPa、28 kPa、30 kPa和32 kPa时，弯矩最大值分别为5513 kN·m、5383 kN·m、5336 kN·m、5321 kN·m和5025 kN·m；前排桩的弯矩最大值分别为4742 kN·m、4644 kN·m、4596 kN·m、4571 kN·m和4557 kN·m。总之，内聚力越小，对桩身最大弯矩影响越大。

图4 桩身弯矩最大值随内聚力变化规律

图5汇总得到前排桩和后排桩桩身剪力随桩长的变化规律。结果表明，其他条件相同的情况下，内聚力对桩身剪力影响较小。

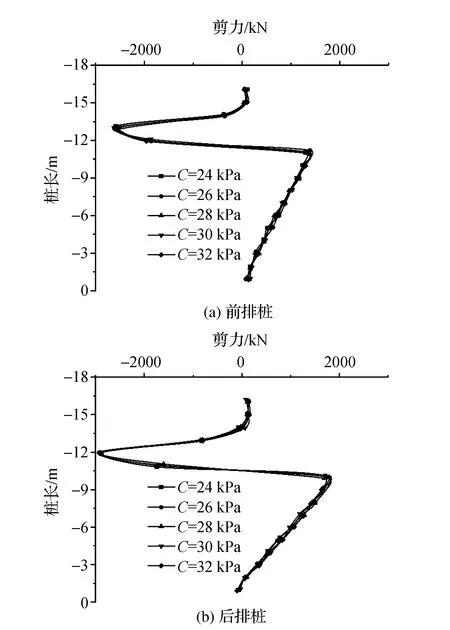
图5 桩身剪力随桩长变化规律

进一步汇总得到桩身最大剪力随内聚力变化规律见图6所示。结果表明，桩身最大剪力随内聚力的增大而减小。随内聚力的增大，最大剪力变化速率变平缓。对于后排桩而言，当内聚力分别为24 kPa、26 kPa、28 kPa、30 kPa和32 kPa时，后排桩剪力最大值分别为2951 kN、2869 kN、2856 kN、2849 kN和2850 kN；前排桩剪力最大值分别为2527 kN、2498 kN、2489 kN和2484 kN。总之，内聚力越小，对桩身最大剪力影响越大。

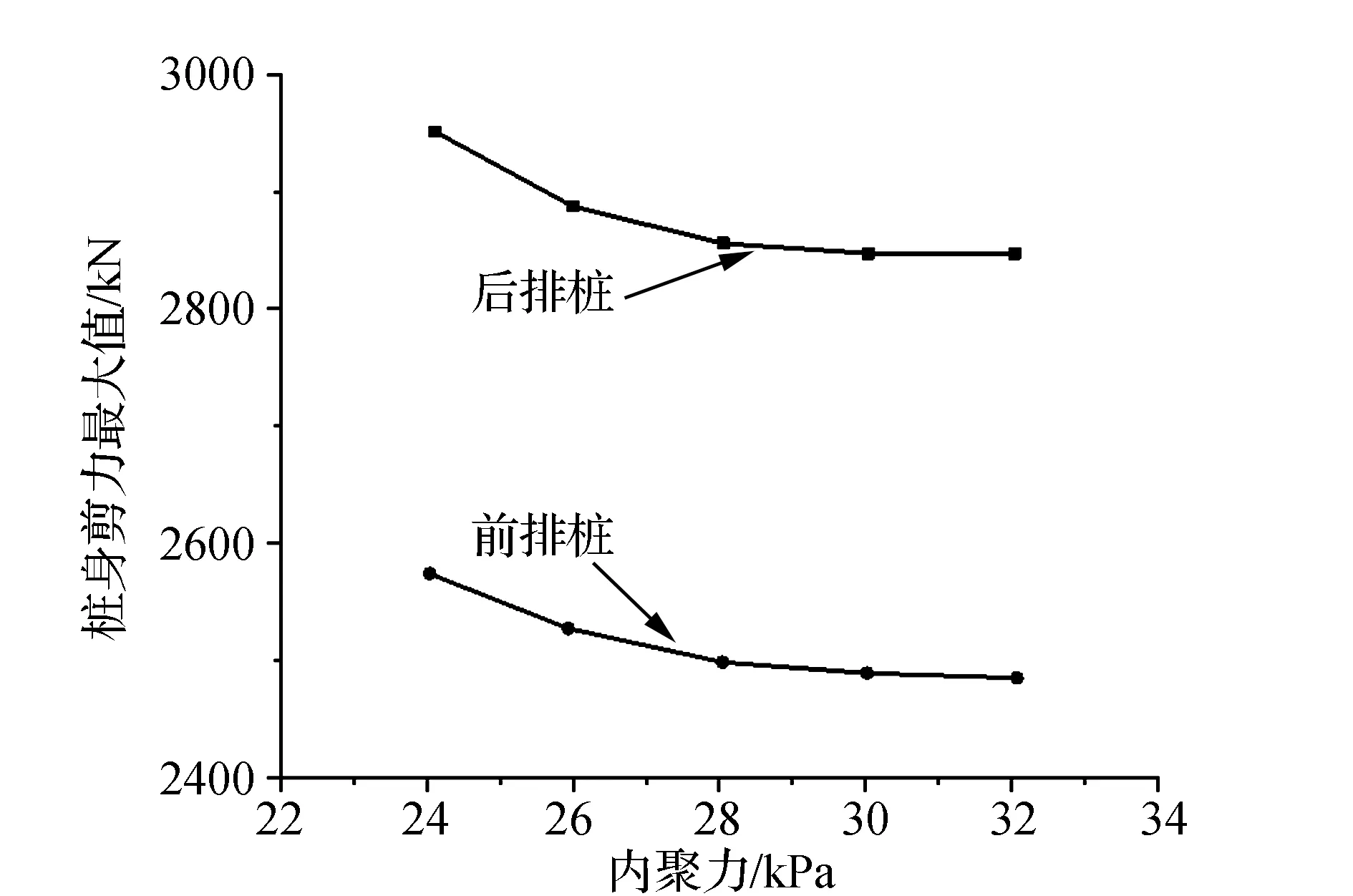
图6 桩身剪力最大值随内聚力变化规律

图7汇总得到抗滑桩承担滑坡推力随内聚力变化规律。结果表明，内聚力比较小时，后排桩承担滑坡推力比例随内聚力的增大而减小，而前排桩随内聚力的增大而增大。当内聚力较大时，不同位置抗滑桩承担滑坡推力比例差异逐渐减小，内聚力大于30 kPa时，两者比例趋于一致。

图7 桩位承担推力随内聚力变化规律

2.2 内摩擦角的影响

图8汇总得到桩顶位移随内摩擦角变化规律。结果表明，在其他条件不变的情况下，桩顶位移随内摩擦角的增大而减小，但随内摩擦角逐渐增大，位移减小速率越来越平缓。也即内摩擦角越小，滑坡推力越大，桩顶位移越大。桩顶位移随内摩擦角的变化规律与图2一致。

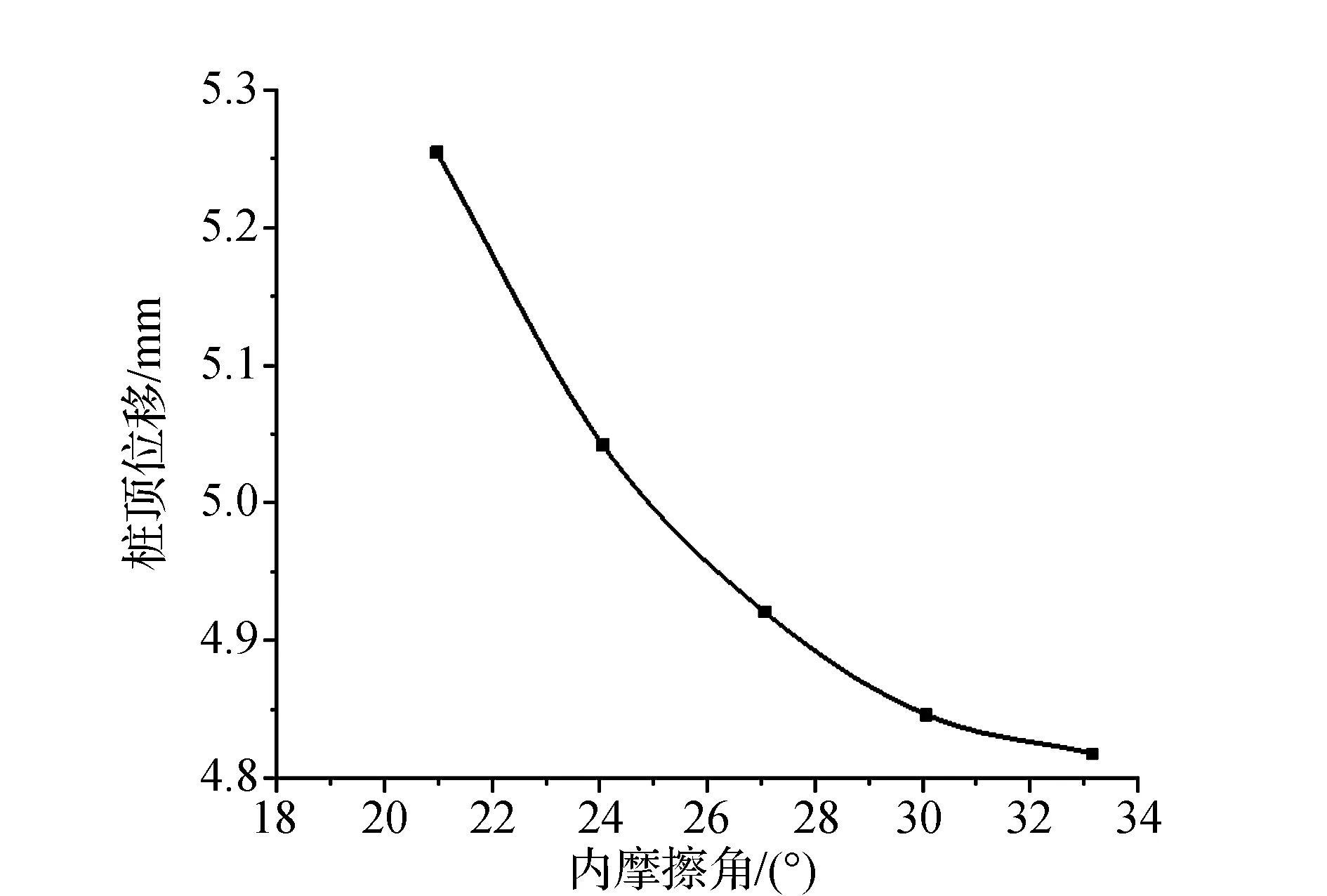
图8 桩顶位移随内摩擦角变化规律

图9汇总得到前排桩和后排桩桩身弯矩随桩长的变化规律。结果表明，其他条件相同的情况下，内摩擦角对桩身弯矩影响较小。

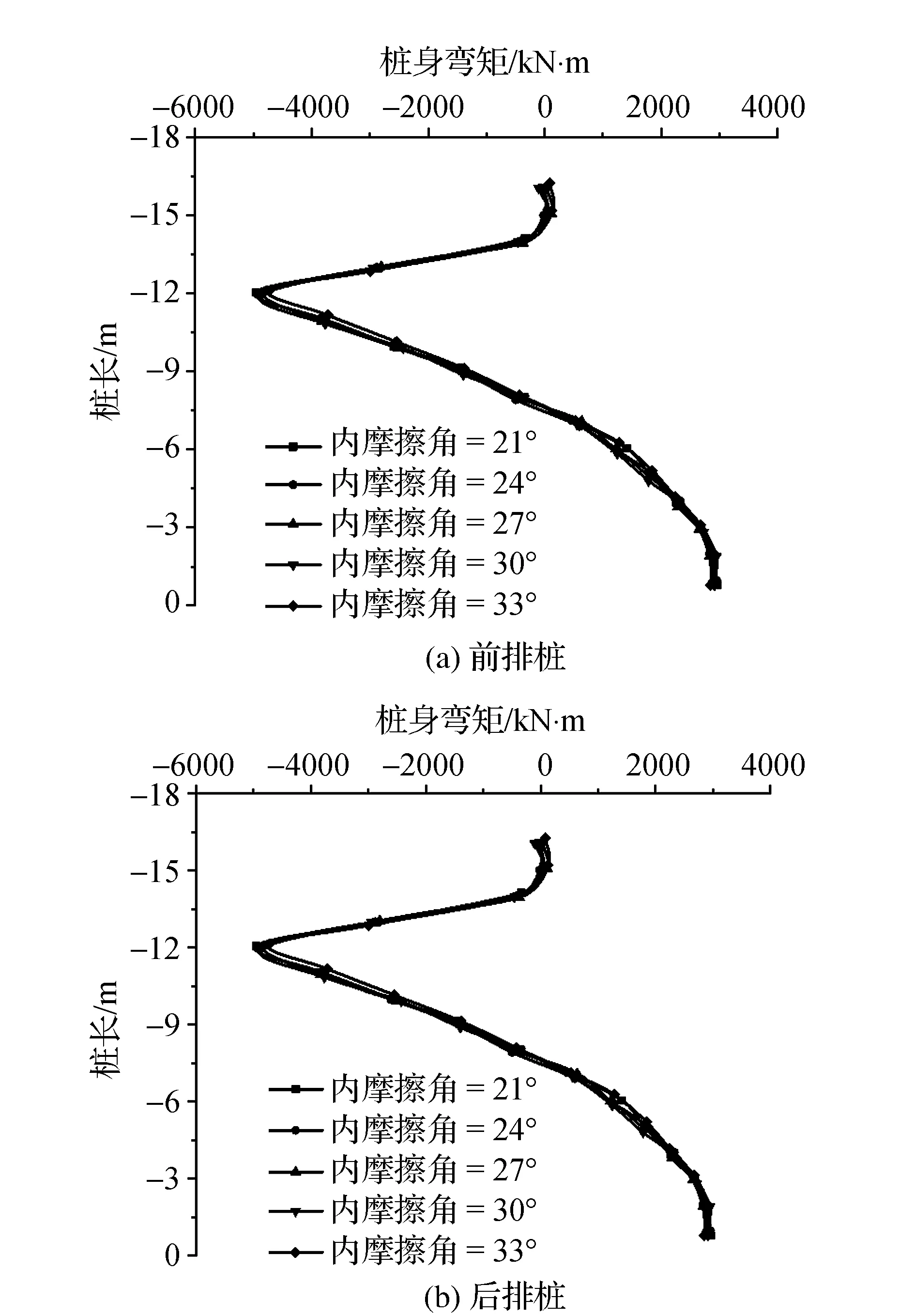
图9 桩身弯矩随桩长变化规律

进一步汇总得到桩身最大弯矩随内聚力变化规律见图10所示。结果表明，桩身最大弯矩随内摩擦角的增大而减小。内摩擦角越大，桩身最大弯矩越小，与内聚力对桩身最大弯矩的影响相比，内摩擦角对最大弯矩的影响更为显著。

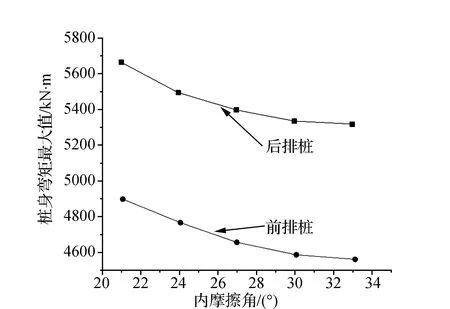
图10 桩身弯矩最大值随内摩擦角变化规律

图11汇总得到前排桩和后排桩桩身剪力随桩长的变化规律。结果表明，其他条件相同的情况下，内摩擦角对桩身剪力影响较小。剪力最大值出现的位置也基本保持一致。因此，改变土体的内摩擦角不会影响抗滑桩的剪力分布。

图11 桩身剪力随桩长变化规律

进一步汇总得到桩身最大剪力随内摩擦角变化规律，见图12所示。结果表明，桩身最大剪力随内摩擦角的增大而减小。内摩擦角越大，桩身最大剪力越小。

图12 桩身剪力最大值随内摩擦角变化规律

图13汇总得到内摩擦角发生变化时，抗滑桩承担滑坡推力比例关系。结果表明，当内摩擦角较小时，后排桩承担滑坡推力的比较逐渐减小，而前排桩承担的比例逐渐增大，但当内摩擦角为33°时，两排桩承担滑坡推力的比例趋于相同。

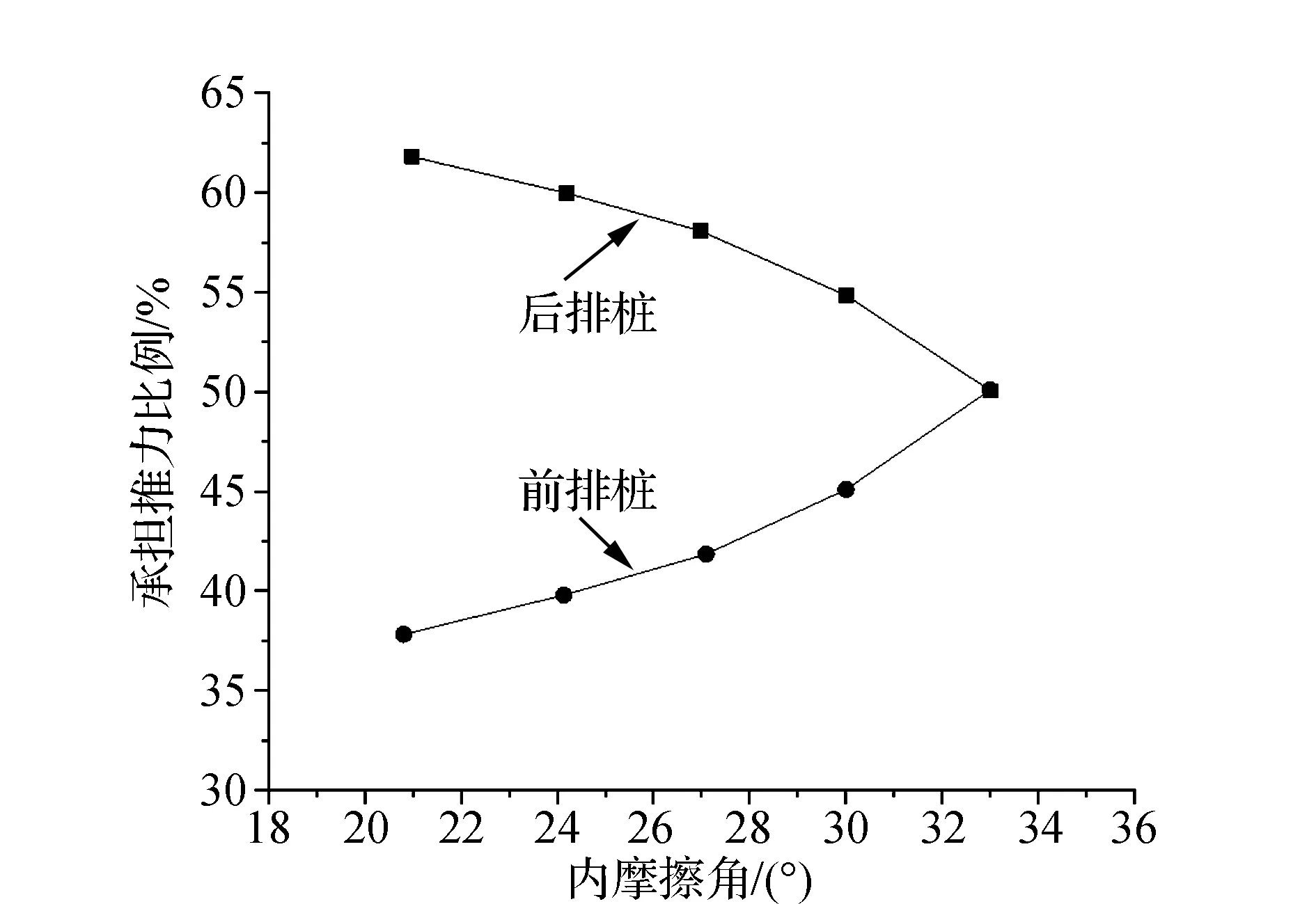
图13 桩位承担推力随内摩擦角变化规律

3 结 论

采用数值有限元研究了土体抗剪强度参数对抗滑桩桩顶位移、桩身弯矩及桩身剪力分布规律s的影响，得到如下结论：

(1)岩土体的抗剪强度参数对抗滑桩的内力分布规律影响不显著，但会显著的影响弯矩最大值和剪力最大值。

(2)当土体的强度参数较小时，参数变化对抗滑桩承担滑坡推力的比例的影响较大，随着抗剪强度参数的增大，对承担滑坡推力比例影响越来越小。此外，土体内摩擦角变化对抗滑桩的弯矩和剪力影响幅度比内聚力变化影响更为显著。