基于强化学习的火星无人机状态约束控制*
田翰文,夏元清,潘振华,王泰祺
北京理工大学自动化学院,北京 100081
1 概述
作为一种新型的火星探测装置,火星无人机可以克服火星车和轨道探测器的一些缺陷,为探索火星、开发火星提供了一条重要的技术途径[1]。目前,火星无人机主要包括浮式气球、固定翼、共轴和转子4种类型:浮式气球研究较早且功能有限,尚未深入研究,固定翼无人机和转子无人机无法获得良好的起降环境,不适合火星飞行。
火星无人机主要扮演2大角色[2]:1)“火星车行驶领航员”。火星无人机在一次飞行中就可完成半径几百米范围的火星地表成像,快速实现周边地形,精准领航火星车安全快速行驶[3]。2)“火星车探测效能倍增器”[4]。火星无人机的飞行速度快,能快速覆盖并掌握周边地表形貌和成分特性,发现并引导火星车快速抵近高价值目标[5],又快又准地实现科学探测,推动火星车对高价值目标探测能力的“倍增”[6]。
苛刻的火星环境对火星无人机技术研究具有极大的挑战[7]。在同轴火星无人机的飞行控制中,由于火星大气稀薄,无人机旋翼升力随旋翼转速的变化范围远小于地球环境,因此火星无人机的飞行位置调整过程较慢。火星风、沙尘暴等现象会严重影响火星无人机的飞行稳定性,这就要求火星无人机能快速适应不断变化的环境,保证无人机的飞行安全。一旦到达火星,无人机必须生存下来,并进行操作。没有任何物理干预的可能性;因此,火星无人机需要适应环境变化和最大干扰(如空气密度、温度、风向、地形特征及光照)[8]。而当前所用的方法为PID控制,对火星无人机的抗干扰能力以及状态约束方面均提升有限,因此控制方法应在地球无人机(UAV)控制方法的基础上考虑抗环境干扰。
火星无人机在多种约束条件下运行[9],例如由外部环境条件、系统性能要求或火星无人机安全问题引起的约束[10-11]。目前,基于障碍Lyapunov函数(或积分障碍Lyapunov函数)的反演控制方法总是涉及到虚拟控制器的可行性条件[12],即虚拟控制器必须满足一定的预定约束区域[13-15],这给相应控制方案的设计和实现带来了很大的困难[16-17]。针对火星无人机是一个连续时间非线性多输入多输出系统,提出了一种考虑输入约束的基于积分强化学习的最优跟踪控制方法。为了避免对持续激励条件的要求,结合了积分强化学习和经验回放技术,并考虑了输入饱和度。
本文基于六自由度运动方程和牛顿-欧拉动力学方程,建立了火星无人机的数学模型,引入了纯粹基于系统状态的非线性状态相关函数。经过坐标变换,通过采用基于障碍Lyapunov函数和积分Lyapunov函数的方法来处理在全状态和非对称约束下的非线性系统,并分别对虚拟控制器的可行性进行评估,经过评判神经网络设计和动作神经网络设计,采用积分强化学习技术建立连续时间系统的Bellman方程误差。提出了一种考虑输入约束的基于积分强化学习的最优跟踪控制方法,完成了火星共轴无人机的位置控制。
2 火星无人机数学模型
火星无人机的严格反馈非线性系统为:
(1)
其中:x1=[x11,x12,x13]T表示无人机的位置,x2=[x21,x22,x23]T表示无人机的速度,ωb=[ωbx,ωby,ωbz]T表示无人机绕x、y、z三轴的角速率,m表示无人机的质量,Fb表示无人机在机体坐标系下所受到的力。
主要受到以下非对称约束:
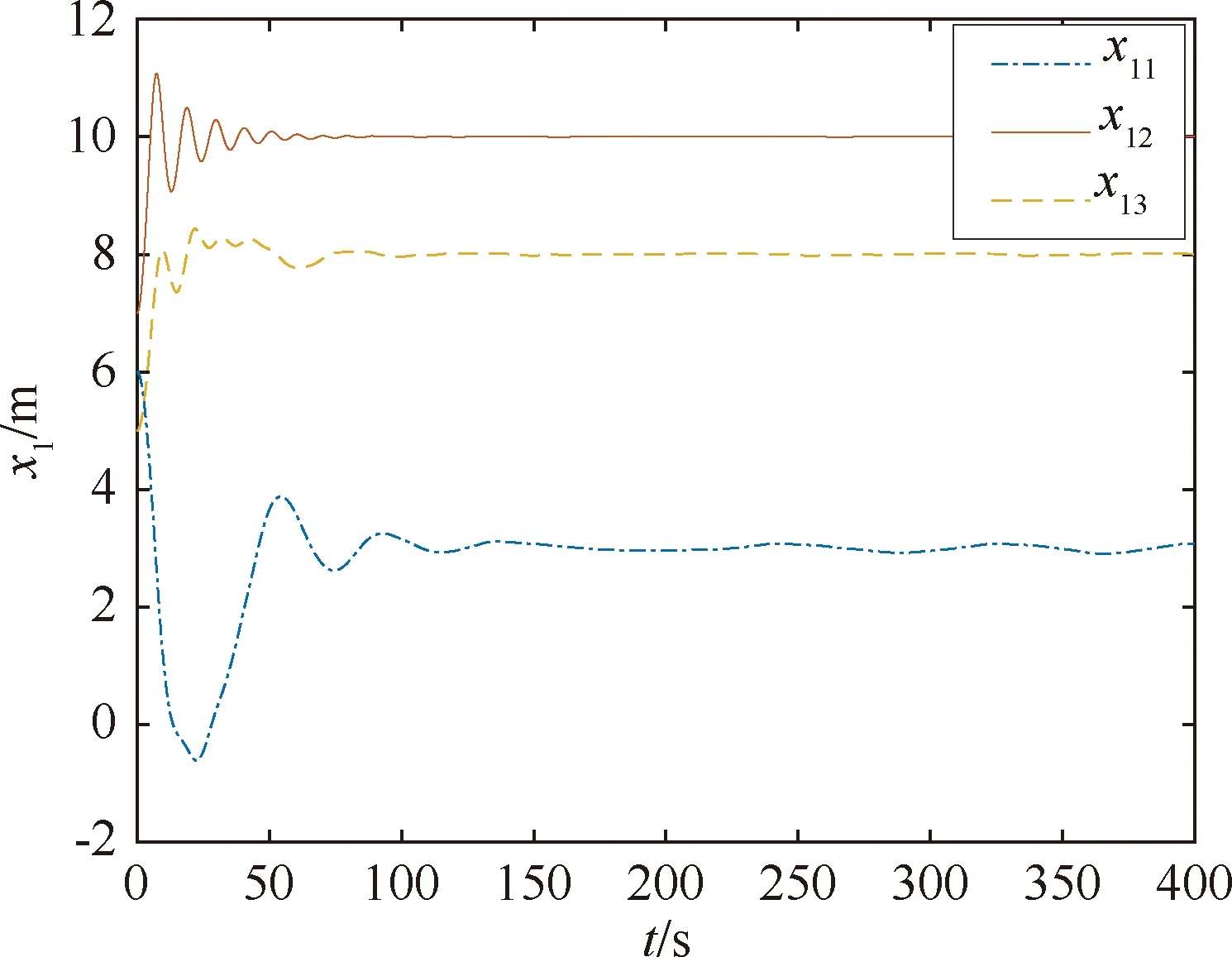
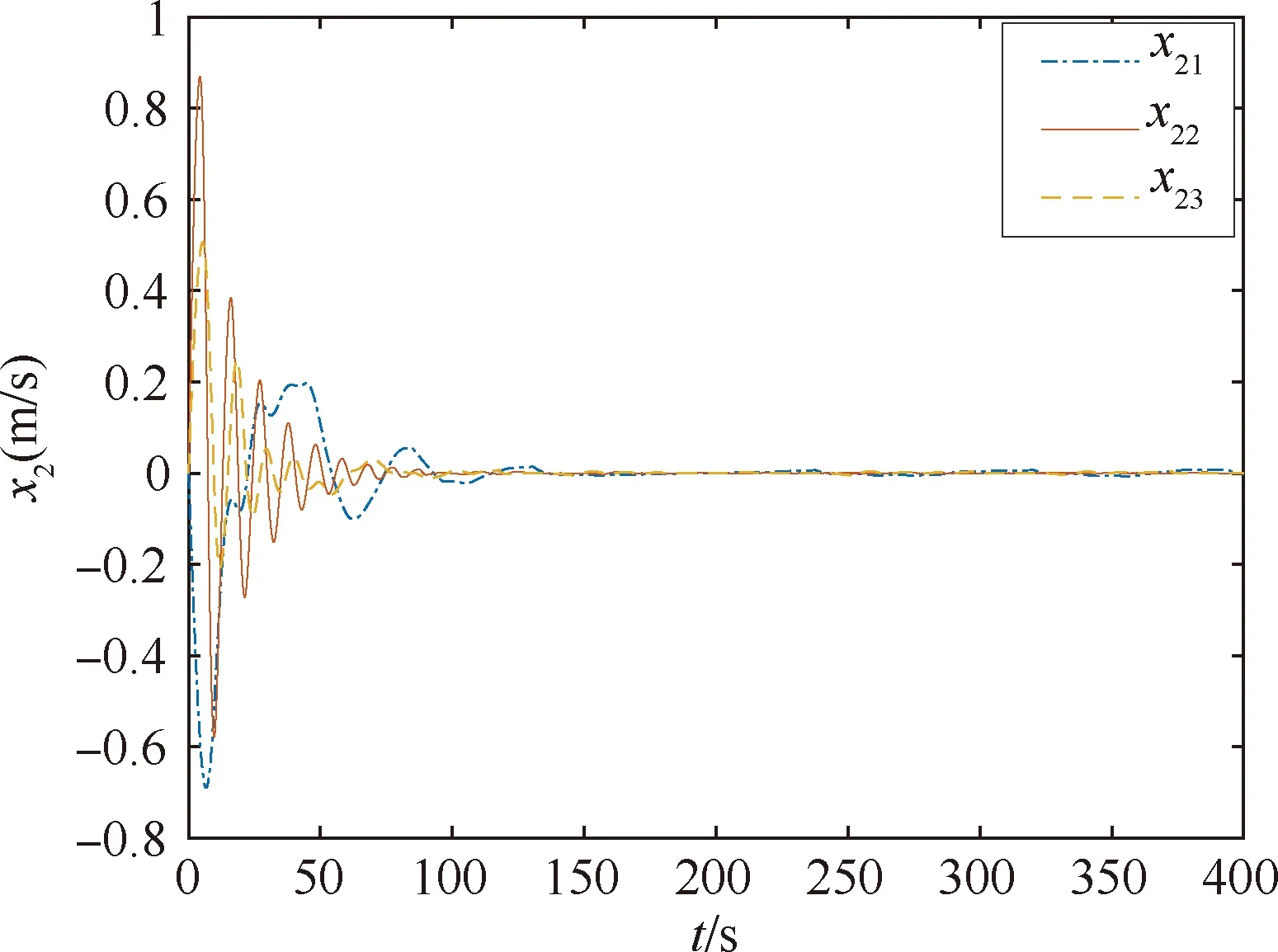
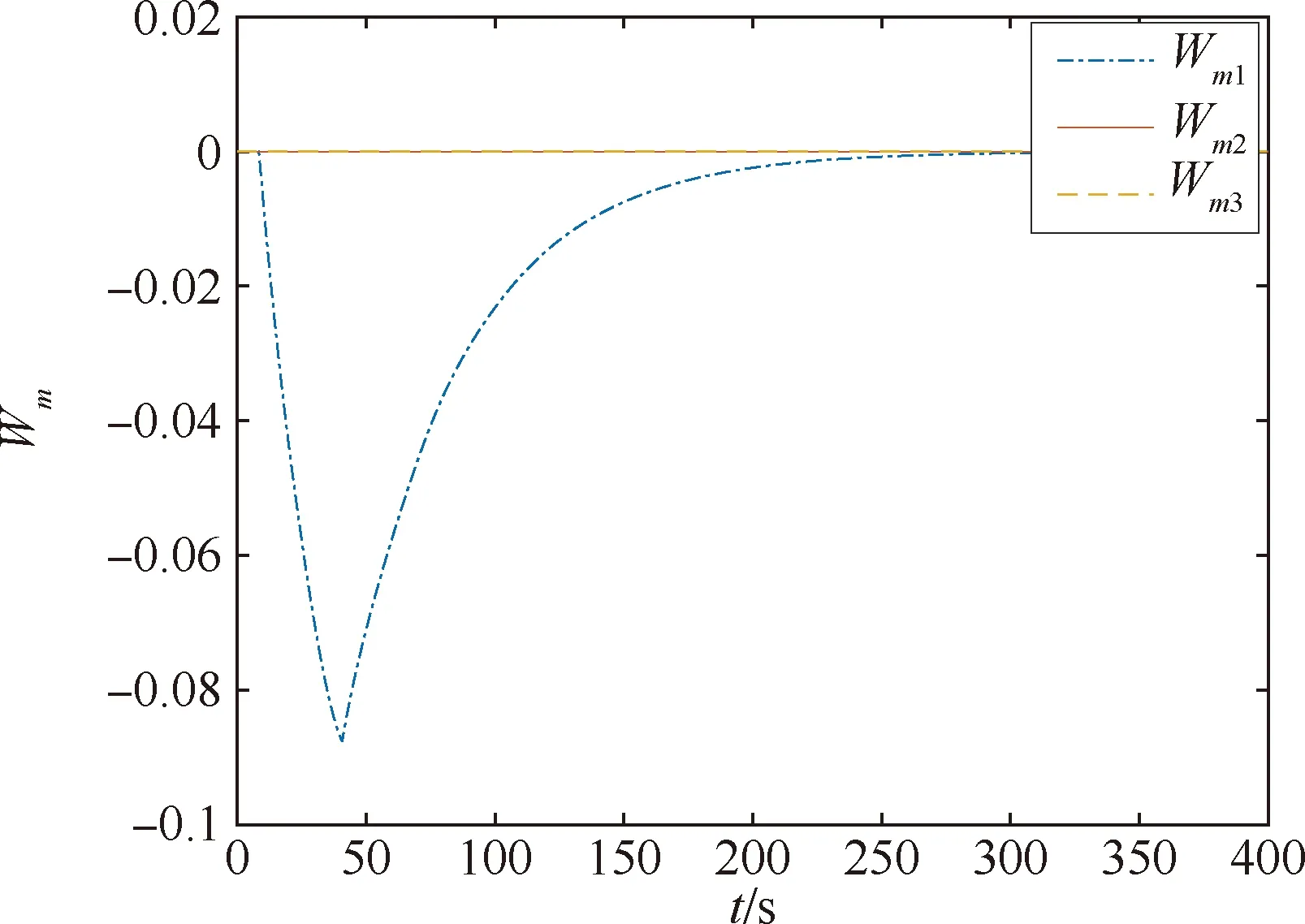
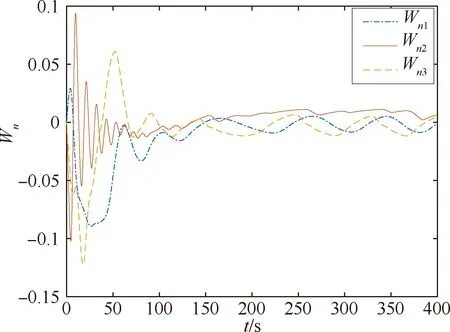
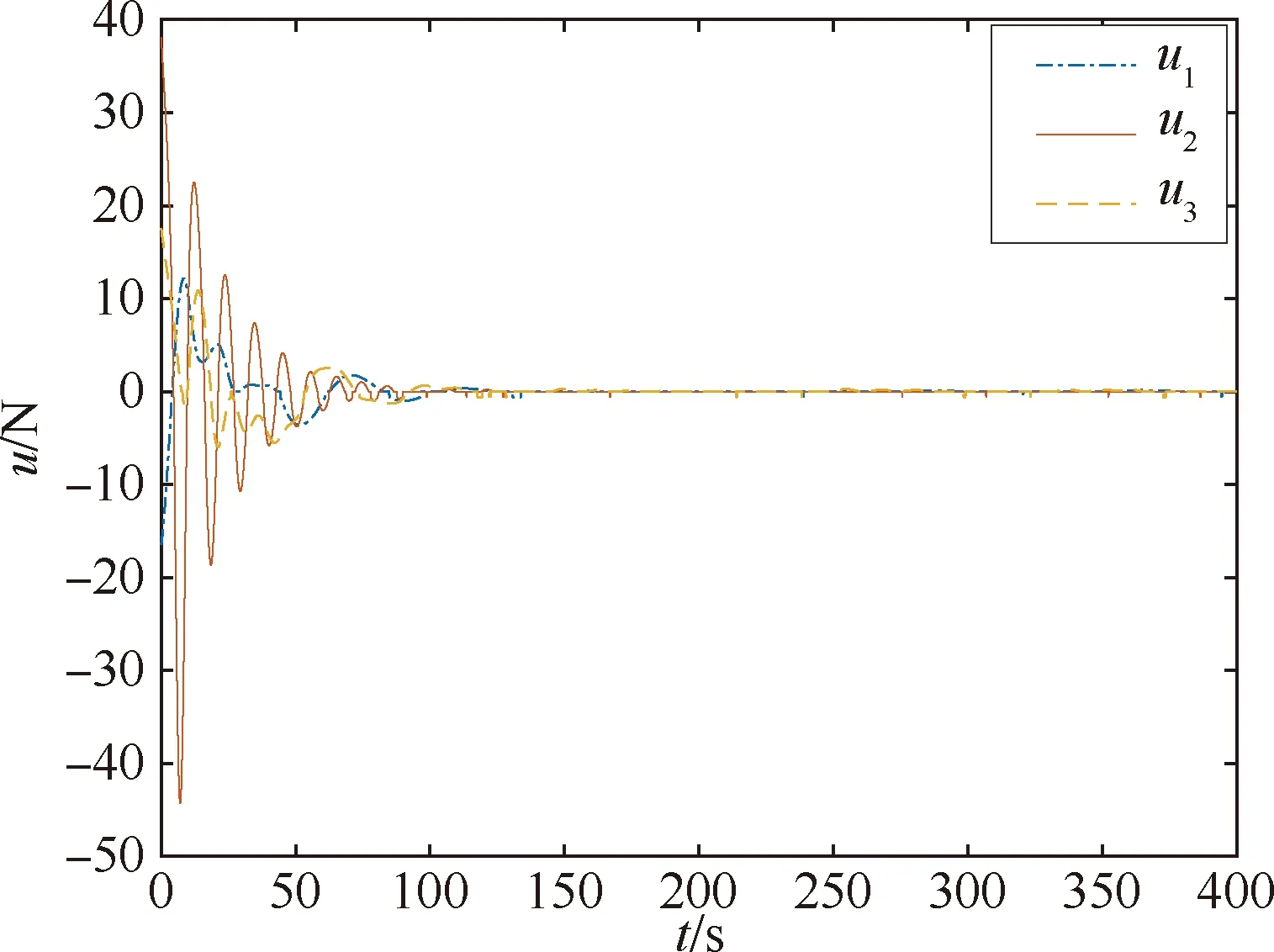
x1i:-K1i (2) 其中:K1i和K2i是已知的正常数。 本文的控制目标是设计火星无人机的自适应神经网络鲁棒控制器,使得系统y(t)的输出紧密跟踪期望轨迹yd(t),并且保证系统最终一致且有界,系统中获得的任何信号都有界。同时,在没有虚拟控制器可行性条件的情况下,继续保持一个完全的非对称状态约束。 根据式(1)~(2),可以得出: (3) g2(x1,x2)u(t)+k(t) (4) 其中:g1(x1,x2)=([g(x1,x2)+gT(x1,x2)]/2),g2(x1,x2)=([g(x1,x2)-gT(x1,x2)]/2)。 g(x1,x2)是一个非奇异矩阵,并且这个非奇异矩阵的弗罗比尼乌斯均值是有界的。 火星无人机的跟踪误差为: h=x1-xe (5) (6) 神经网络是一种通用逼近器,可用于逼近紧集中的未知函数。神经网络具有良好的抗干扰能力,可以有效降低火星环境下恶劣环境对无人机的影响。因此,激活函数一般为径向基函数。对于紧集Ω中定义的f(x)∈R3,x∈R3,可以用f(x)个典型线性参数RBF神经网络来逼近。 f(x)=W*Tφ(x)+χ(x) (7) 其中:W*是神经网络的权重矩阵,χ(x)是近似误差,φ(x)是基函数向量。 (8) 其中:cri∈R3表示RBF神经网络中心,σNN表示基函数的宽度。由于一般的近似性质,我们可以得到N>0,且如果N>N0,那么χ(x)→0。 本节将指定一个长期的表示度量,然后通过使用积分强化学习技术来解决这个长期成本。未知的控制方向需要用Nussbaum型函数求解。基于Barrier Lyapunov函数的控制技术通常将状态约束问题转化为跟踪误差问题,从而对系统的初始状态产生更多的约束。此外,大多数先前的理论通常是在对称约束的简单情况下发展起来的。为了能够求解非对称状态约束,列出了火星无人机位置状态的非线性相关函数: (9) 且可以得到: (10) 对于任何具有状态约束的严格反馈系统,基于障碍Lyapunov函数或积分障碍Lyapunov函数的控制方法都会涉及到所提出的可行性条件。 -K1i<α1i(t) (11) 其中:α1i(t)代表虚拟控制率。对于虚拟控制律α1,即虚拟控制α′1ivs,虽然依赖于状态变量和其他待设计参数,但要始终保持在相应控制方案可行的区域内显然是不切实际的,因为找到这些参数很困难,甚至是不可能的。 引理2对∀l∈Rq和p>0,L=llT+pIq和λmin(L)=c是正定对称矩阵,并满足: 1)当l=0,L=pIq是正定的; 2)当∀l≠0,因为llT的特征值是[1,0,…,0],L的特征值是[p+1,p,…,p],所以L是正定对称的。 在本节中,针对具有非对称状态约束的严格反馈非线性系统(火星无人机)提出了一种基于鲁棒自适应的新型控制方案。该控制器设计的关键在于,它不直接使用基于坐标变换的通用设计方法z2=x2-α1,也不直接使用基于坐标变换的一般DCS方法z2=x2-α2f,其中xi表示系统状态,α1表示虚拟控制器,α2f是一阶滤波器的输出。 将坐标变换设计如下: (12) (13) (14) (15) 另外可以得到: (16) 其有助于进行稳定性分析,该方法不需要复杂的离线约束优化程序来获得最优设计参数。 定义火星无人机的长期性能指标为: (17) 情形1:zi2(t)>>cpi,zi2(t)≥max{K12,K22},∀ξ∈[t-T,t) 情形2:zi2(t)≥cpi,zi2(t)≤min{|K12|,|K22|},∀ξ∈[t-T,t) 情形3:zi2(t) 设计以下公式: (18) 其中:阈值设计为cqi>0。式(18)可以不断提高火星无人机适应环境的能力。 跟踪误差仅限于状态约束条件: 上述的情形1中zi(t)远大于cqi,qz=1代表较差的跟踪性能。当火星无人机受到干扰,系统状态越界时,可以利用强化学习将系统拉回约束区域。上述的情形2中zi(t)大于等于cqi,qz=0.3表示具有一般的跟踪性能,0.3是根据火星无人机的控制特性进行设计。上述的情形3中zi(t)小于cqi,qz=0表示具有优秀的跟踪性能。 “1”表示U(t)增加,代表当前的控制会导致很大的跟踪误差,“0”表示U(t)减小,代表当前的控制得到了很好的控制效果。cqi是一个很小的常数,如1,0.1和0.01。我们利用U(t-T)和U(t)之间的关系,设置了cqi=0.02,并设计了连续时间非线性系统的贝尔曼误差。 γ-1(U(t)+qc) (19) 从式(18)可以得出,qc=[qc1,qc2,…,qcn]T,并且 (20) 由式(19)可以发现,U(t)包含了火星无人机中未来系统的信息。无法直接获得信息的问题很难直接解决,需要特殊的功能设计和适当的设计参数。通常使用值函数近似。用临界RBF神经网络对其进行逼近 (21) (22) U(t-T)可以估计为 (23) 由于xe是先验已知的,所以可以选择它为xm。设计 xm(t)=[x1T(t),sT(t),xeT(t+Te),…,xeT(t+NeTe)]T Ne是指定的数字,Te是时间间隔。 因此,时间误差可以写为: (24) (25) (26) 针对火星无人机连续时间非线性多输入多输出系统,提出了一种基于积分强化学习的状态约束神经网络控制方法。为了估计系统的不确定性,设计了一种作用径向基函数神经网络来估计火星无人机系统的不确定性: (27) (28) 定义动作神经网络的权值误差 (29) (30) (31) 尽管f(x1,x2)和g(x1,x2)都是未知的,但本文研究了主要的未知控制方向。这意味着g(x1,x2)不会出现在u(t)里。一般来说,用评判RBF神经网络近似f(x1,x2)是估计火星无人机动力学不确定性的一种方法。 (32) (33) 下面进行控制器设计: 第1步:求得时间的导数: (34) (35) (36) (37) 通过在式(15)和(17)中对z2和y2的定义,得到: (38) (39) (40) 通过使用杨氏不等式: (41) (42) (43) (44) 可以得出: (45) 将式(45)代入式(40)可得: (46) (47) 最终给出了虚拟控制律: (48) (49) (50) (51) 因此: (52) 最终得出: (53) 第2步:取z2的导数作为时间收益率 (54) 选择李雅普诺夫函数 (55) (56) 实际控制律u表示如下: (57) (58) 其中:c2,γ2和σ2是正的设计系数。 定理1根据火星无人机的连续时间系统模型,考虑评判神经网络和动作神经网络。基于此设计的自适应积分强化学习神经网络控制器具有式(27)和式(40)的更新特性,在初始值有界时还具有以下特性: 1)在火星无人机闭环系统中,任何信号都是半全局均匀且最终有界的; (59) 同时,设计了动作神经网络σn σn>bφmbφn (60) 本节在Matlab/Simulink环境下进行数值模拟验证。在考虑外部干扰和执行器死区特性的情况下,控制目标是使火星无人机在100 s内达到所期望的状态,并给出了火星共轴双旋翼无人机的仿真结果。 给定无人机的各项参数为:火星无人机质量为1.8 kg,无人机的姿态角为[0.2,0.1,1.5]Trad,初始位置为[6.1,6.9,5.1]Tm,预期位置为[3.1,10,8.03]Tm。 假设火星无人机的系统干扰上限为1.2×10-3N。设计的控制器参数及所期望轨迹Sp表示如下: (61) 设计了控制器的积分区间为T=0.1,γ=0.88,δ=1。同时,状态约束的函数参数为K11=3,K21=-5,K12=K22=-15。所设计的位置控制回路的参数为c1=[0.06,0.06,0.06]T,设计速度控制回路的参数为c2=[16,16,16]T。此外,还设计了一系列强化学习评判神经网络的参数Γc=0.08,σc=0.16。 最后,将强化学习动作网络的参数设计为Γa=0.01,σa=0.1。 仿真程序运行了400 s,火星无人机的位置如图1所示,x轴在T=64.1 s后趋于稳定,y轴在T=75.8 s后趋于稳定,z轴在T=130.8 s后趋于稳定,三轴均达到所需位置。图2显示了火星无人机的三轴速度。可以看出,当T=79.5 s时,y轴和z轴的速度趋于0,当T=133.3 s时x轴的速度趋于0,当无人机到达所需位置时,速度将变为0。 图1 火星无人机位置变化曲线 图2 火星无人机速度变化曲线 图3 评判神经网络输出变化曲线 图4 动作神经网络输出变化曲线 控制器u的应用程序输出如图5所示。在初始阶段,对于较大的跟踪误差,输出变化很大,控制器达到稳态的时间相对较快,在T=97.8 s时达到。在稳态阶段,控制器α1,u的输出是稳定的。因此,控制器的稳定性可以通过状态有界性来实现。 图5 控制器u输出曲线 如果约束条件很小,则这些最优设计参数将不可用。但在给定的控制条件下,对虚拟控制器α1没有约束,也不需要使用复杂的算法来寻找最合适的参数,因此,该方法更有效。 针对共轴双旋翼火星无人机非线性系统抗干扰能力的问题,提出了一种基于强化学习和状态约束的连续时间非线性系统自适应神经网络控制方法。严格的理论分析表明,闭环系统是稳定的;保证所有闭环信号一致且最终有界。设计了一个RBF神经网络来近似它。利用运动神经网络逼近未知漂移动力学,求解未知控制方向。通过严格的李雅普诺夫函数证明,得到了闭环的稳定性和一致极限的有界性。同时,我们将权重误差和跟踪误差限制在一个紧集,所设计的算法可以有效地提高火星无人机的环境适应性。采用李亚普诺夫函数和积分李亚普诺夫函数方法处理非线性系统,避免了将状态约束转化为新的误差边界和虚拟控制器的可行性条件。仿真实验和数据表明本研究提出的方法可以使火星无人机在恶劣环境下稳定飞行,增强了对环境的适应能力。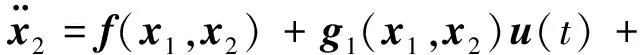
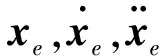
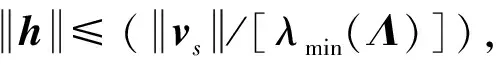
3 神经网络函数近似
3.1 神经网络函数设计
3.2 非线性状态函数
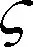
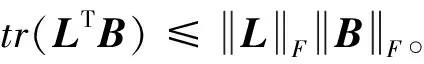
4 控制方向未知的积分强化学习
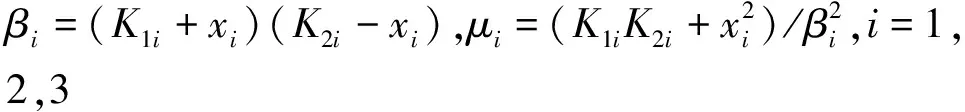
4.1 评判神经网络设计
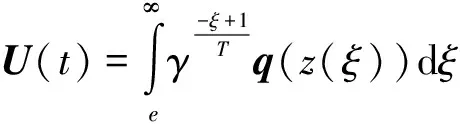
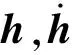
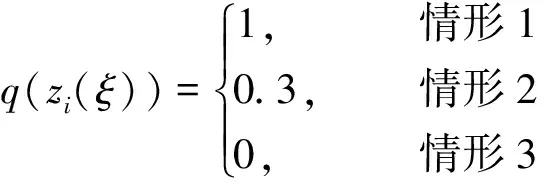
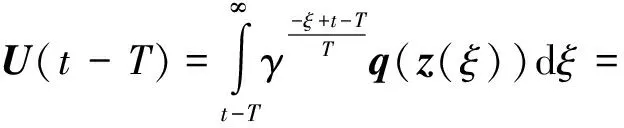
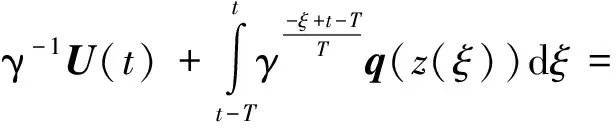
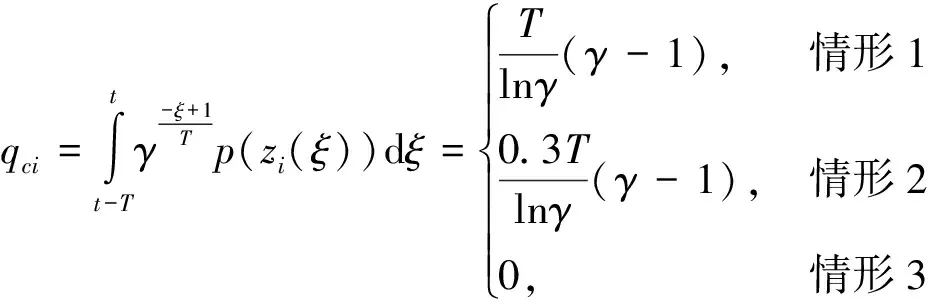
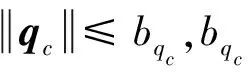

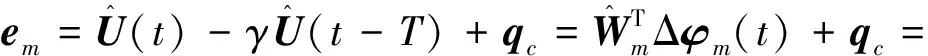
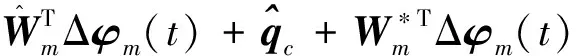
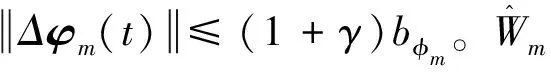
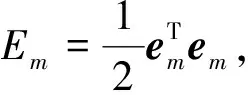
4.2 动作神经网络设计

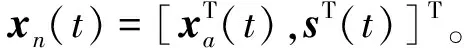
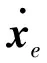
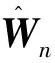

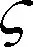
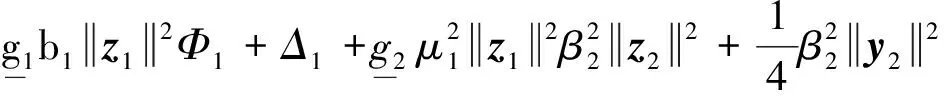
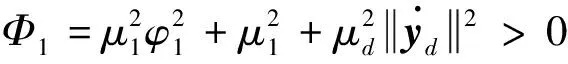
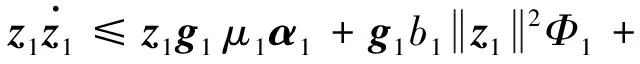
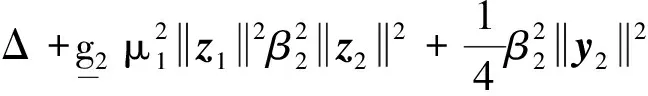
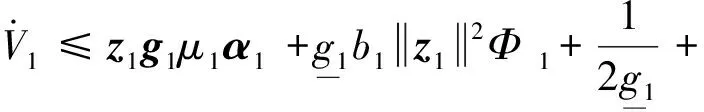
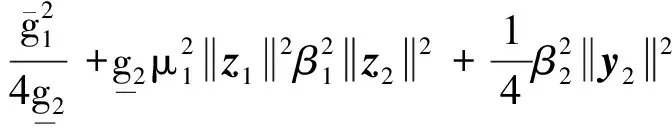
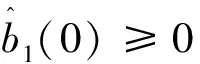

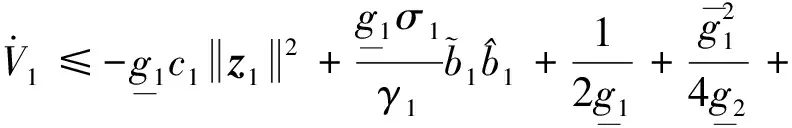
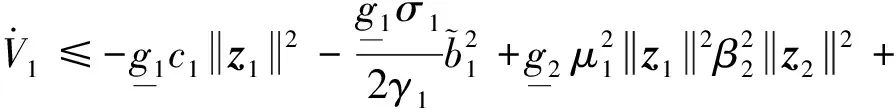

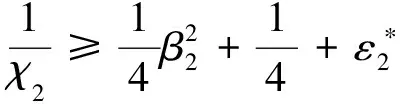
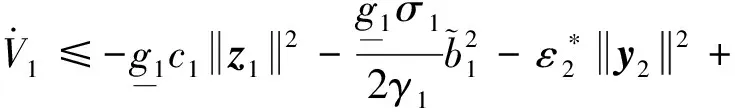
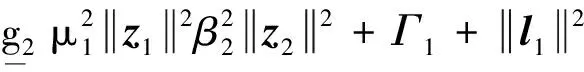
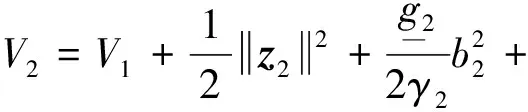
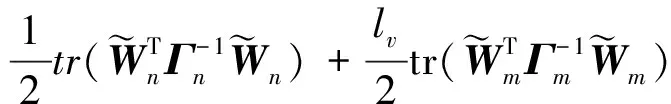
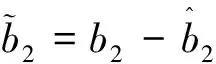
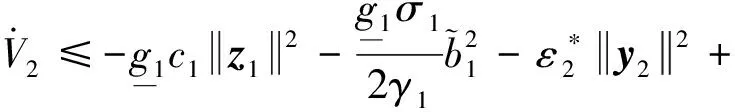

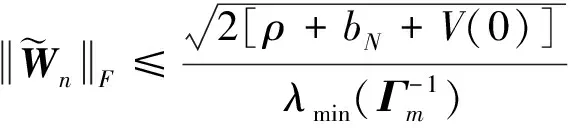
5 仿真验证与分析
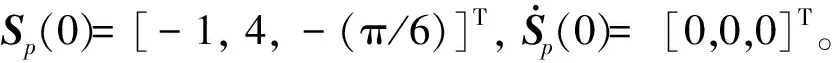

5 结论

