基于Lebesgue和熵度量的不完备邻域决策系统特征选择
余 清 侯丽萍
(信阳职业技术学院数学与计算机科学学院 河南 信阳 464000) 2(信阳农林学院信息工程学院 河南 信阳 464000)
0 引 言
随着大数据处理技术的发展,数据量呈指数级增长,收集到的大量信息中可能含有大量噪声、冗余或缺失的特征值[1]。因此,在使用海量数据之前,有必要对其进行预处理。特征选择作为一个重要的预处理步骤,其主要目标是消除冗余和噪声特征,并对其进行处理缺失值,对数据进行分类,并为数据应用程序提取有用的信息[2]。
近年来,特征选择在模式识别、机器学习和数据挖掘应用等领域引起了学者们的广泛关注。传统的粗糙集模型作为一种流行的属性约简工具,只能处理分类数据集,而不适合解决混合数据集和不完全数据集中数值数据不完整和连续的问题。为了解决数值数据集离散化过程中的信息丢失问题,许多学者引入邻域粗糙集来研究特征选择。在不完备决策系统中,文献[3]提出一种基于邻域容忍条件熵的启发式特征选择算法,文献[4]基于不完备决策系统中的容忍关系,构造了一种基于正区域的属性约简方法。文献[5]在邻域粗糙集中,通过增加相似类与某些决策类具有最大交集的样本来扩大正区域。但是上述方法存在特征冗余问题,并且特征选择算法在一定程度上处理高维数据集时仍有较高的时间消耗。
信息熵作为一种重要的不确定性度量在特征选择及其变体中得到了广泛的研究,提出一种利用邻域粗糙集中的条件判别指数进行特征选择的方法[6]。另外文献[7]研究了邻域互信息及其在高光谱波段选择分类中的应用,然而这些不确定性度量的单调性并不总是成立的,而且这些基于邻域粗糙集的特征选择文献也只是从完备信息系统的信息观角度进行研究集合,许多现有的特征选择方法通常只基于代数视图或信息视图,对于大规模、高维的数据集,这些方法仍然是低效的。
为解决上述问题,提出一种基于Lebesgue和熵度量的不完备邻域决策系统特征选择方法。将邻域粗糙集与Lebesgue度量相结合,解决了不完备信息系统中基于邻域粗糙集的特征选择方法不能处理无限集的问题,并有效地处理了混合和不完备数据集分类问题。通过数据集验证了本文方法的有效性。
1 Lebesgue和基于熵的不确定性度量
1.1 基于Lebesgue度量的依赖度
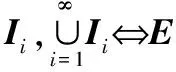
(1)
Lebesgue内部度量可以表示为m*(E)=|I|-m*(I-E)。如果m*(E)=m*(E);那么,可以说E是可测量的,写为m(E)。在本文中,m(X)被统一视为集合X的Lebesgue度量,即|X|。
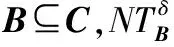
(2)
性质1[8]假设对于任何P、Q⊆C和x∈U,存在具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉;然后,以下属性条件成立:
m(U)=|U|
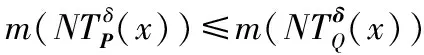
定义2假设对于任何B⊆C,x,y∈U,存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉;然后,根据Lebesgue度量,分别定义X⊆U,X相对于B的邻域上近似集和邻域下近似集,分别为:
(3)
(4)
定义3假设一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,对于任意B⊆C,U/D={d1,d2,…,dl,…},基于Lebesgue度量,D相对于Β的正区域定义为:
(5)
式中:POSB为查找函数;dj∈U/D,j=1,2,…,l,…。
命题1假设存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉且任意Q⊆P⊆C。然后,POSQ(D)⊆POSP(D)和m(POSQ(D))≤m(POSP(D))。
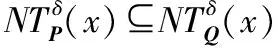
定义4假设对于任何B⊆C,存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,并且U/D={d1,d2,…,dl,…};然后,基于Lebesgue度量将D相对于B的依赖程度定义为:
(6)
式中:dj∈U/D,且j=1,2,…,l,…。
命题2假设一个不完备邻域决策系统INDS=〈U,C,D,δ〉,具有非空无限集U和任意Q⊆P⊆C,γQ(D)≤γP(D)保持不变。
证明对于任何Q⊆P⊆C,根据命题1,m(POSQ(
D))≤m(POSP(D))。因此,根据定义4,可以得到γQ(D)≤γP(D)。
1.2 Lebesgue与邻域容差熵的不确定性度量
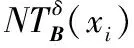
(7)
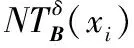
(8)
命题3假设具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,对于任何Q⊆P⊆C,NTEδ(Q)≤NTEδ(P)成立。

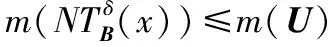
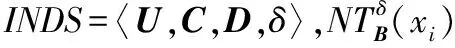
(9)
式中:dj∈U/D,且j=1,2,…,l,…。
引理1[9]假设具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,对于任何Q⊆P⊆C,NTEδ(Q∪D)≤NTEδ(P∪D)成立。
命题4假设对于任何B⊆C和xi∈U,dj∈U/D={d1,d2,…,dl,…},存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,其中j=1,2,…,l,…,则NTEδ(B∪D)≥NTEδ(B)。
证明从定义6和定义7可以立即得出:
NTEδ(B∪D)-NTEδ(B)=
(10)
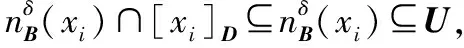
根据命题4,邻域容差联合熵的值大于特征子集的邻域容差熵的值。因此,可以得出结论,当添加新特征时,邻域容差联合熵具有更强的区分能力。
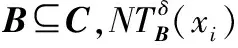
(11)
式中:dj∈U/D,以及j=1,2,…,l,…。
性质2[9]假设存在具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,并且对于任何B⊆C,D对B的依赖程度为γB(D),B和D的邻域容差联合熵为NTEδ(B∪D),则NTDE(B,D)=γB(D)·NTEδ(B∪D)≥0。
从定义8和性质2可以看出,在代数视图中,γB(D)是D对B的依赖程度,而在信息视图中,NTEδ(B∪D)是B和D的邻域容差联合熵。因此,定义8可以基于Lebesgue和熵度量从代数视图和信息视图分析和测量不完备邻域决策系统的不确定性。
2 不完备邻域决策系统中的特征选择方法
2.1 基于邻域容差依赖联合熵的特征选择
命题5假设对于任何Q⊆P⊆C,U/D={d1,d2,…,dl,…},存在具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,其中dj∈U/D且j=1,2,…,l,…。NTDE(Q,D)≤NTDE(P,D)。
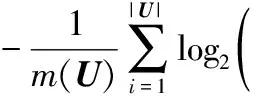
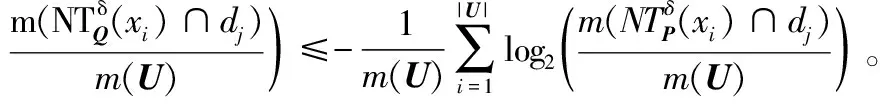
定义9假设存在一个不完备邻域决策系统INDS=〈U,C,D,δ〉,并且有一个非空的无限集U和B⊆C;如果NTDE(B,D)=NTDE(C,D),并且对于任何a∈B,则存在NTDE(B,D)>NTDE(B-{a},D)。可以说B是C相对于D的约简。
定义10假设对于任何B⊆C和a∈B,存在具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉。然后,将B中的属性a相对于D的内部显著性定义为:
Siginner(a,B,D)=NTDE(B,D)-NTDE(B-{a},D)
(12)
定义11假设存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,B⊆C;如果任何a∈B的Siginner(a,B,D)>0,则B中的属性a是必要的;否则,a是不必要的。如果B中的每个a是必要的,则B是独立的。
定义12假设存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,B⊆C;如果对于任意a∈C,NTDE(C,D)>NTDE(C-{a},D),即Siginner(a,C,D)>0,则a称为C相对于D的核心属性。
定义13假设对于任何B⊆C和b∈C-B,存在一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉。然后,将属性b关于D的外部显著性定义为:
Sigouter(b,B,D)=NTDE(B∪{b},D)-NTDE(B,D)
(13)
性质3[9]假设存在一个具有非空无限集U和任意B⊆C的不完备邻域决策系统INDS=〈U,C,D,δ〉,然后,可以得到下述特性:
(1) 对于任意a∈C,0≤Siginner(a,C,D)≤1。
(2) 对于任意b∈C-B,0≤Sigouter(b,B,D)≤1。
(3) 当B=C时,Sigouter(,C,D)=0。
(4) 当且仅当Sigouter(b,B,D)=0时,任何b∈C-B都是不必要的。
请注意,在具有非空无限集U和B⊆C的INDS=〈U,C,D,δ〉中,对于任何a∈B,在计算Siginner(a,B,D)时,NTDE(B-{a},D)仅因为NTDE(B,D)是一个常数而被计算。同样,对于任何b∈C-B,在计算Sigouter(b,B,D)时,仅需要计算NTDE(B∪{b},D)。
2.2 两种代表性约简方法比较分析
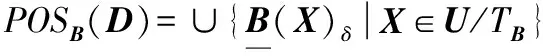
命题6假设存在一个不完备邻域决策系统INDS=〈U,C,D,δ〉,具有非空无限集U和任何B⊆C;如果B是不完备邻域决策系统中C相对于D的邻域容差约简;那么,在不完备邻域决策系统中,B是C相对于D的一个正区域约简。
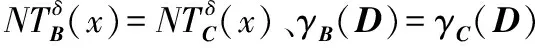
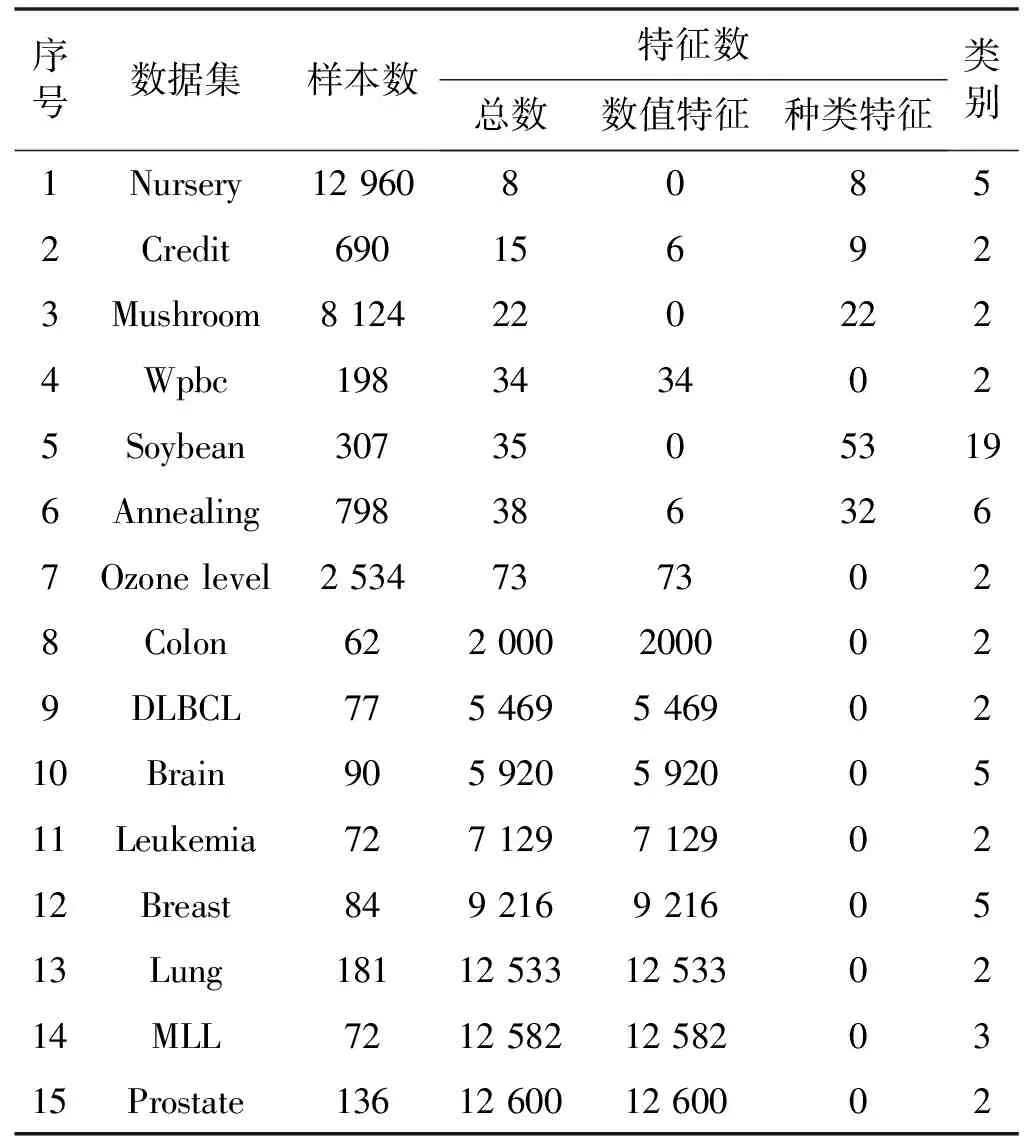
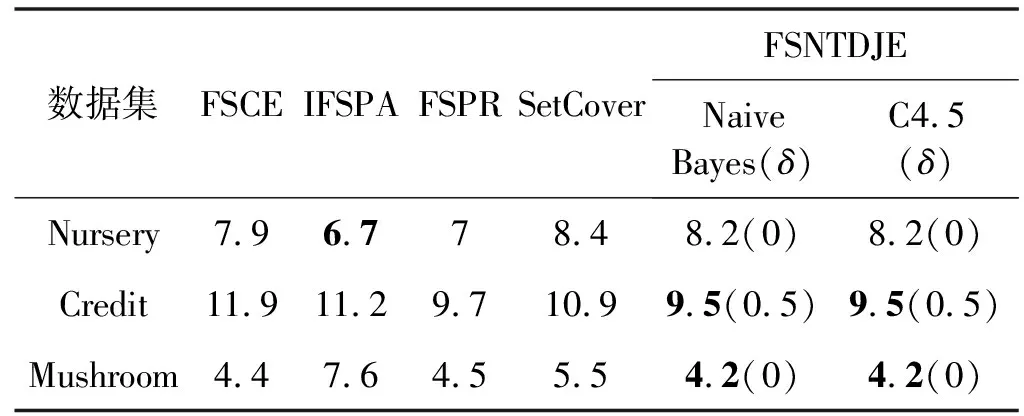
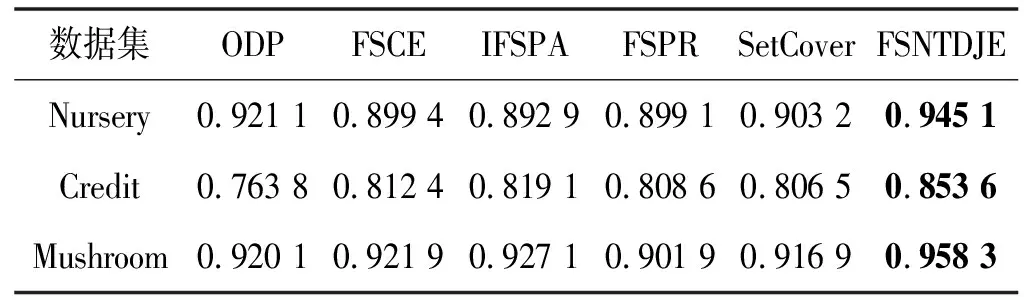
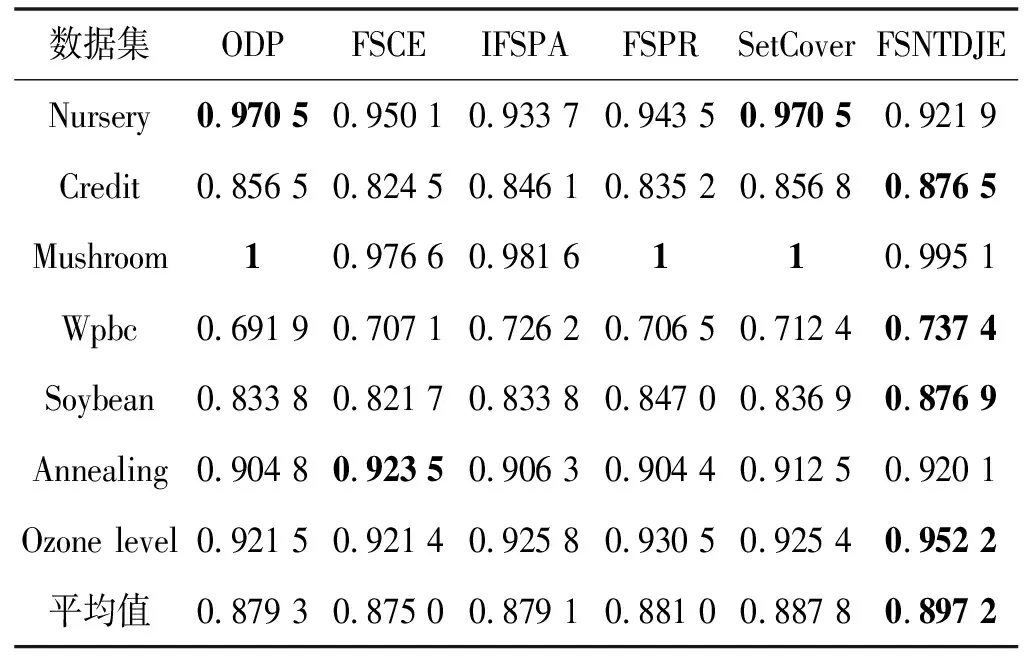
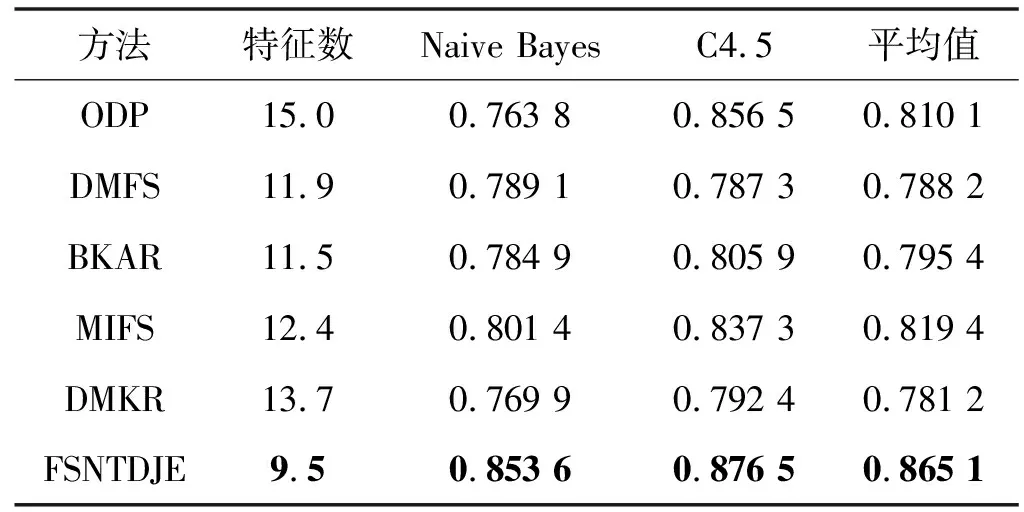
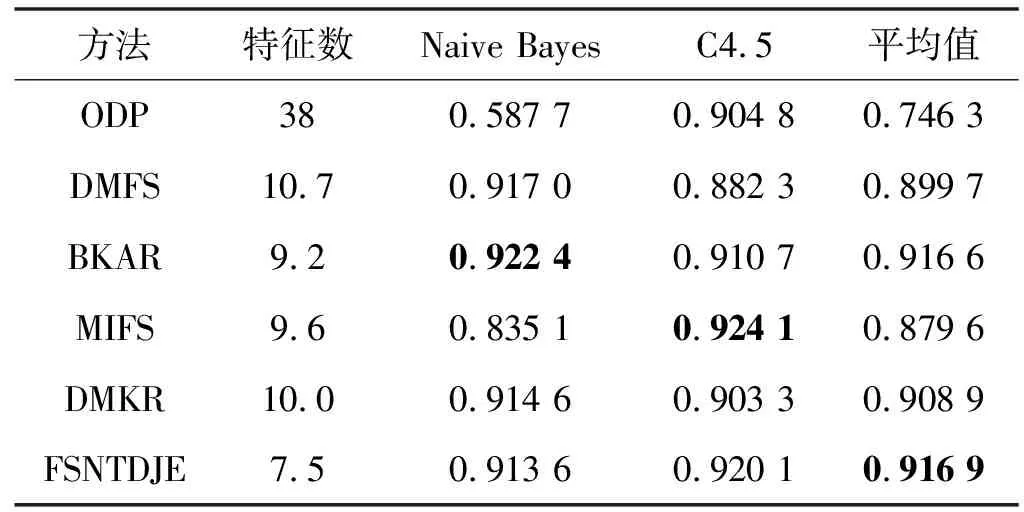
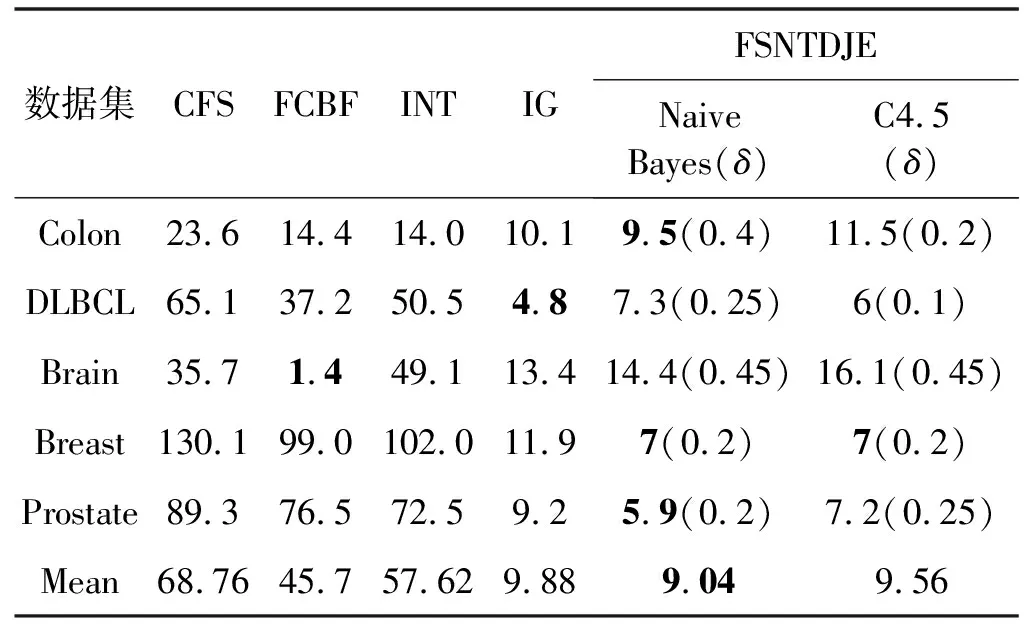
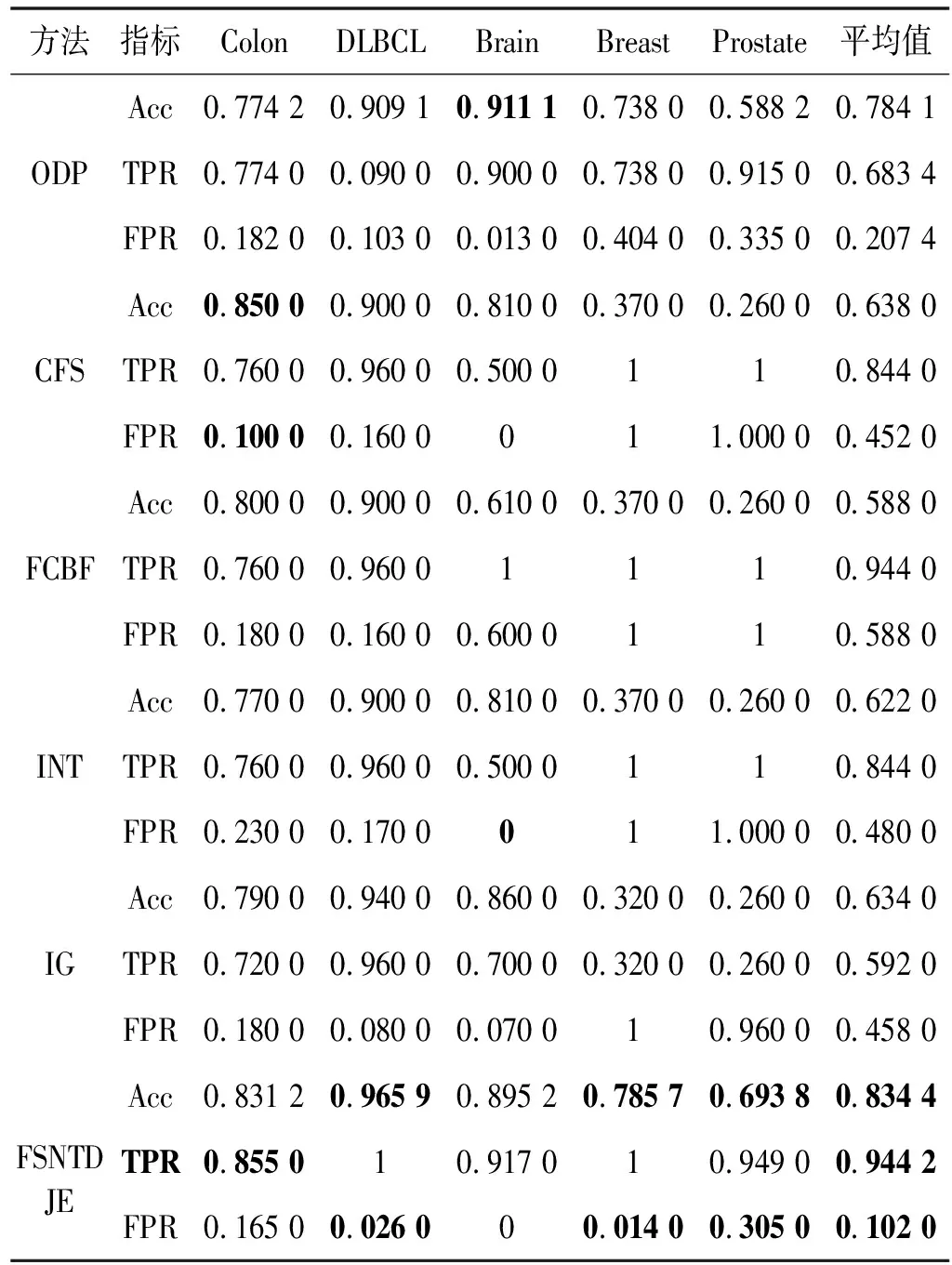
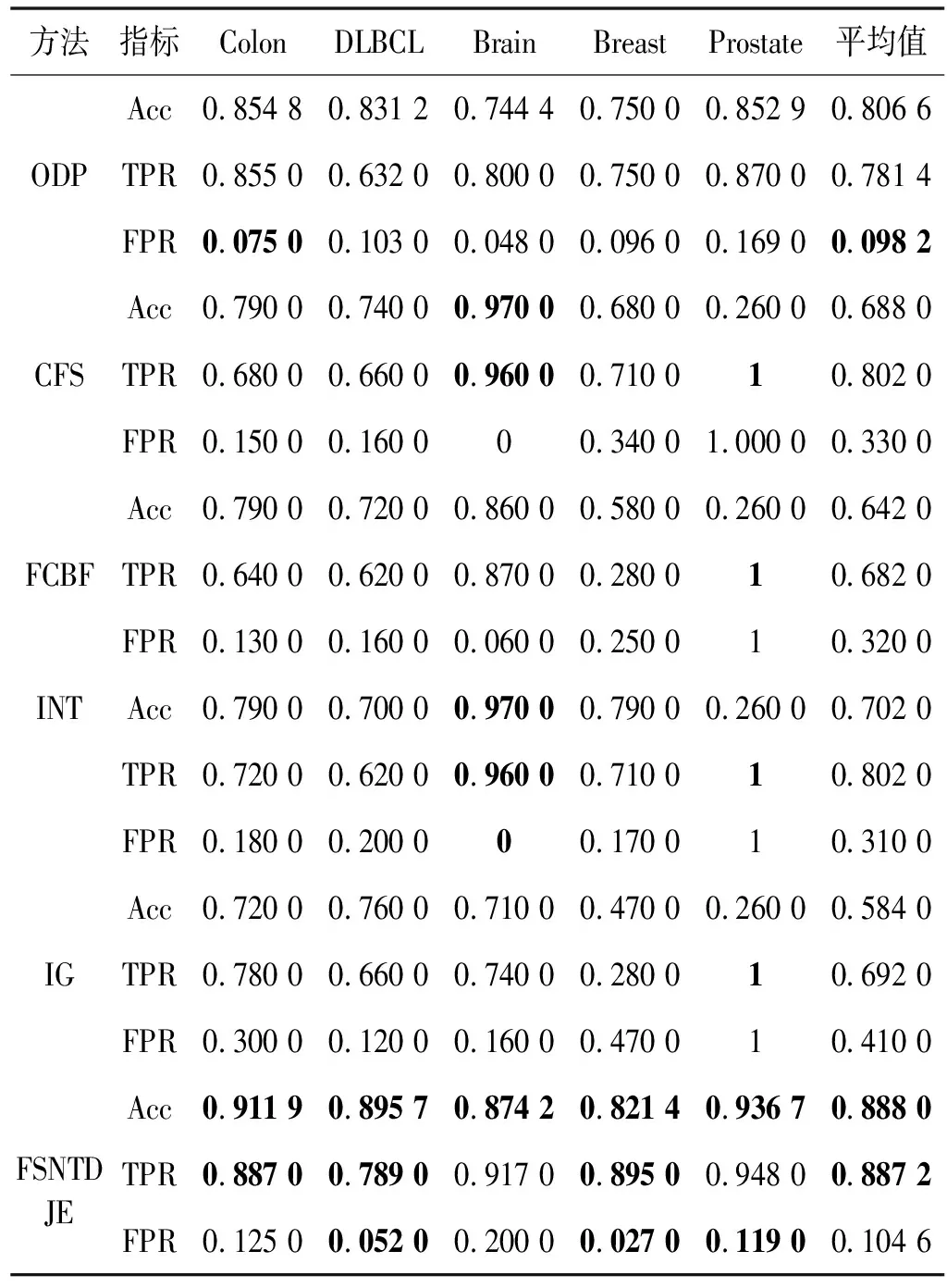
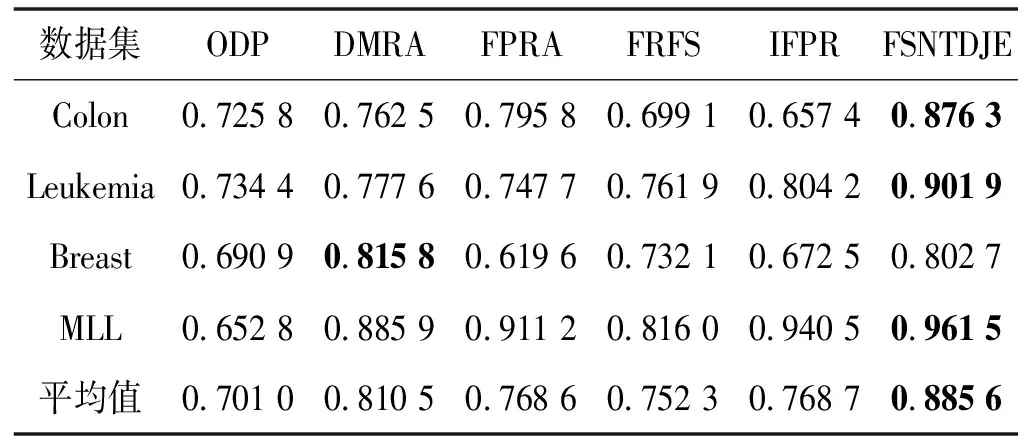
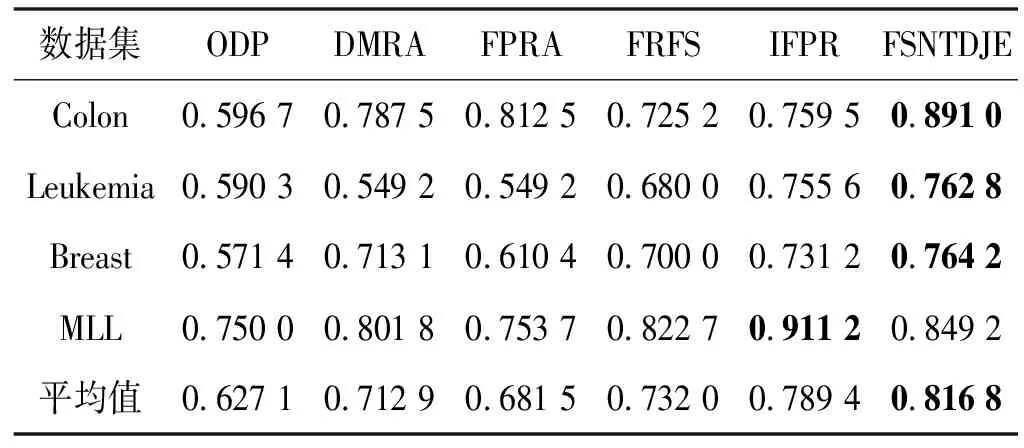
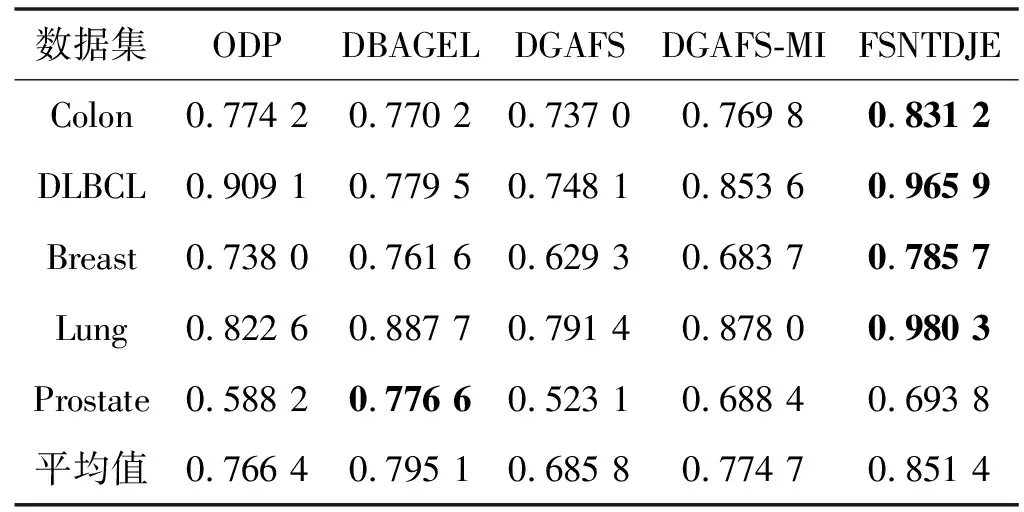
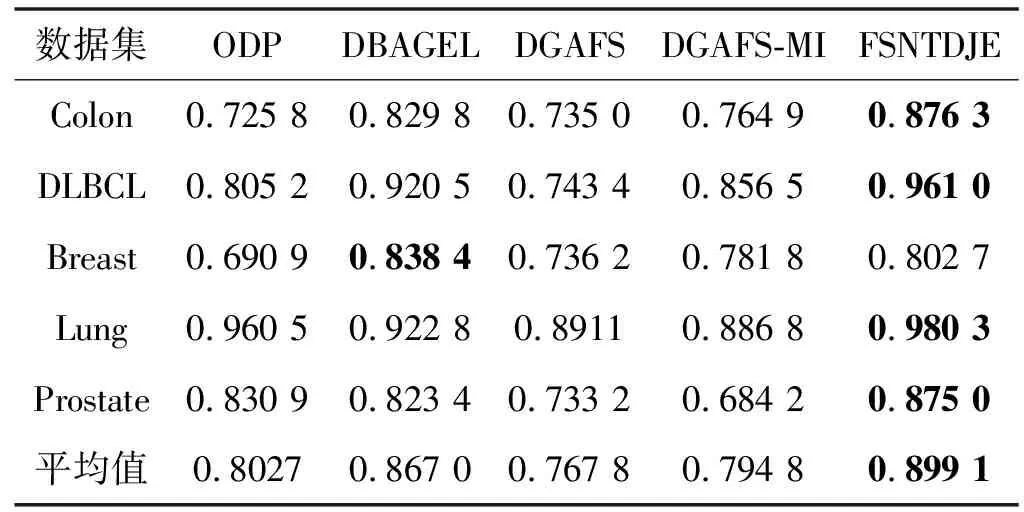
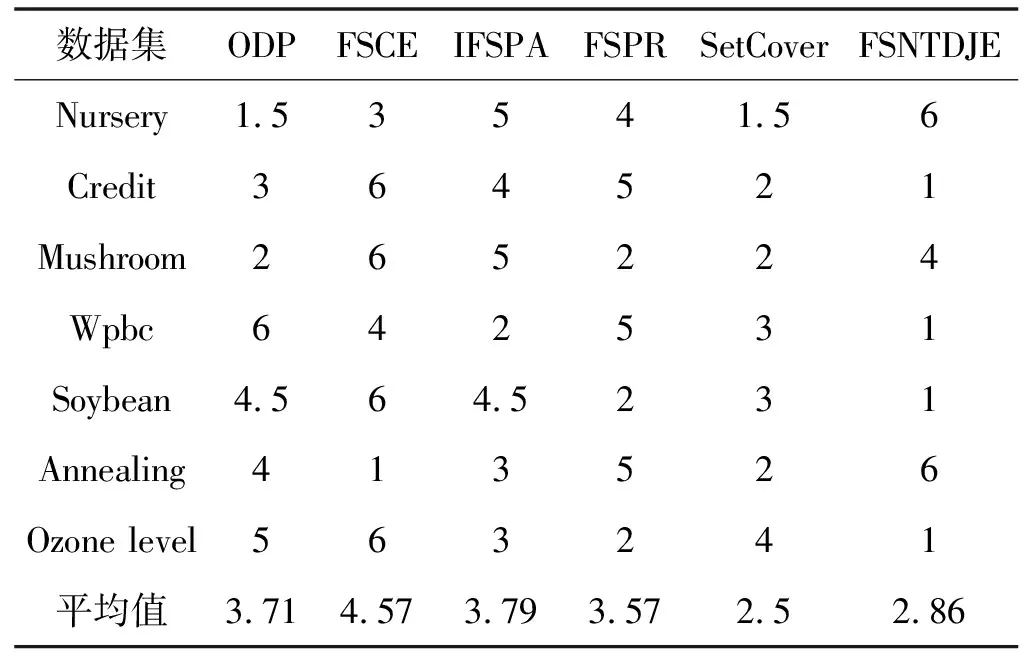
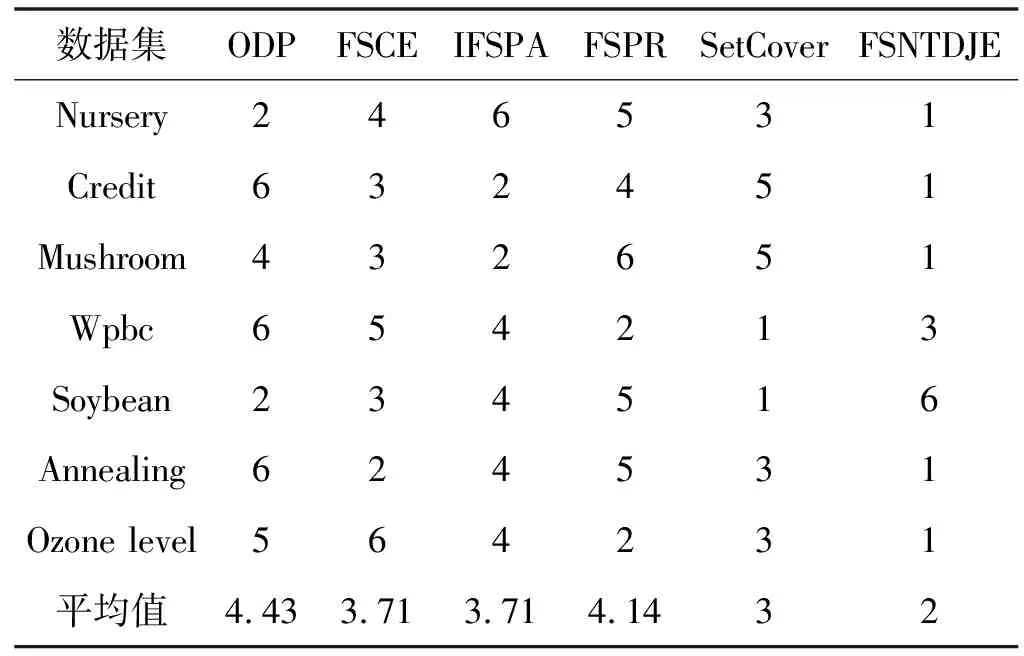
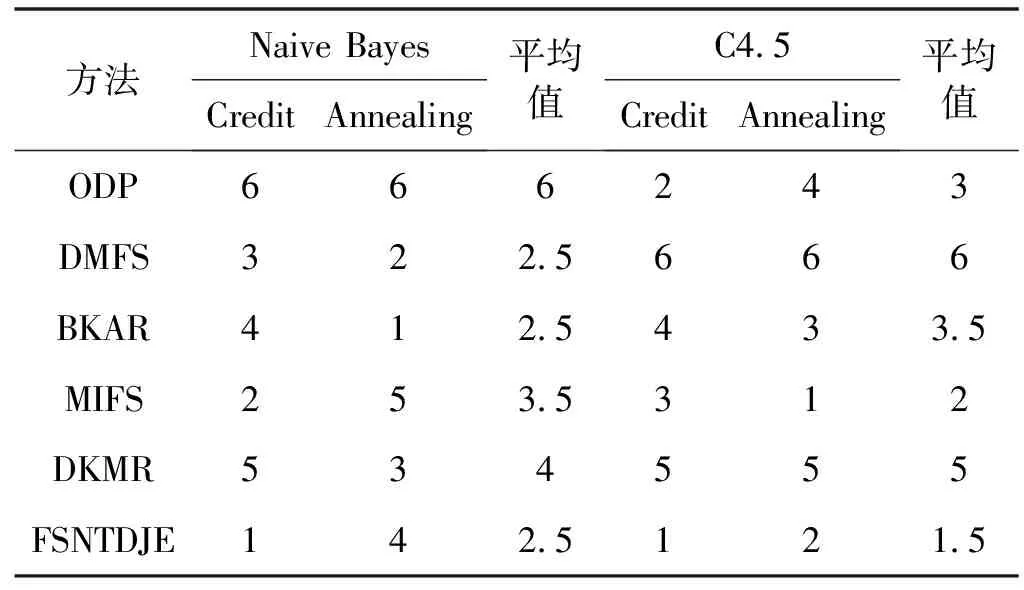
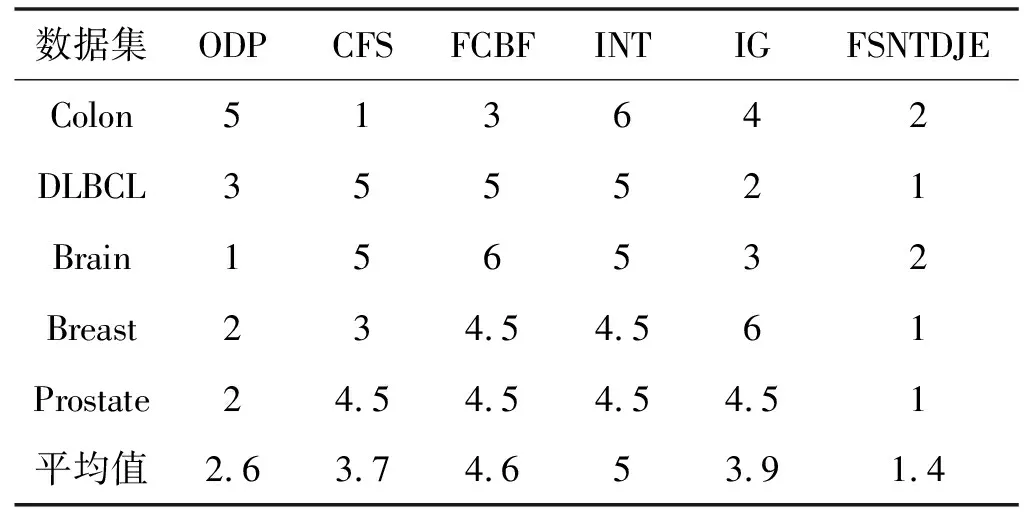
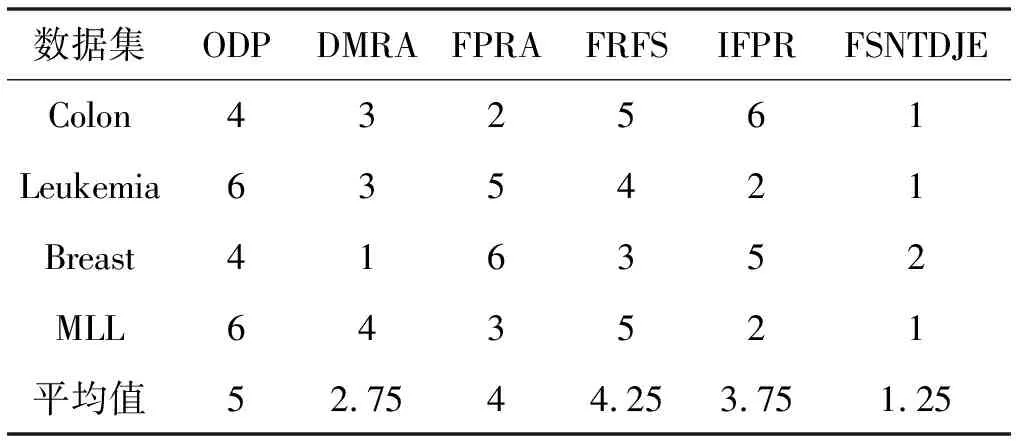
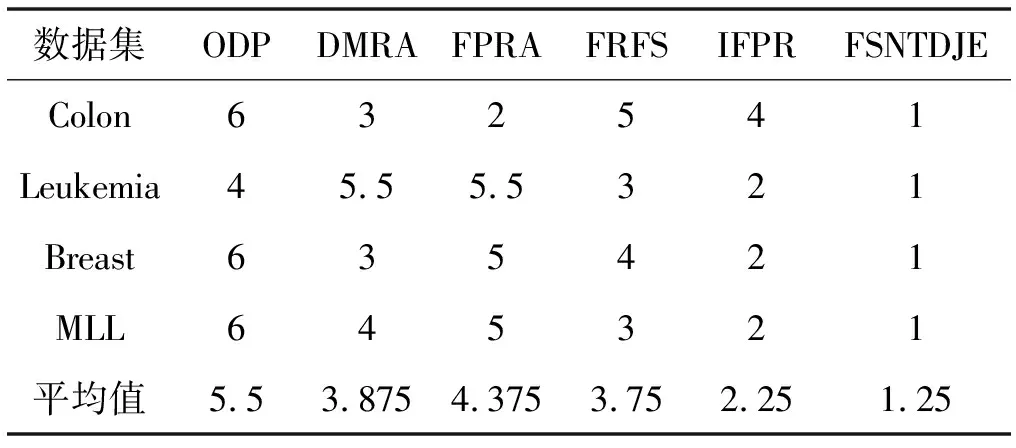
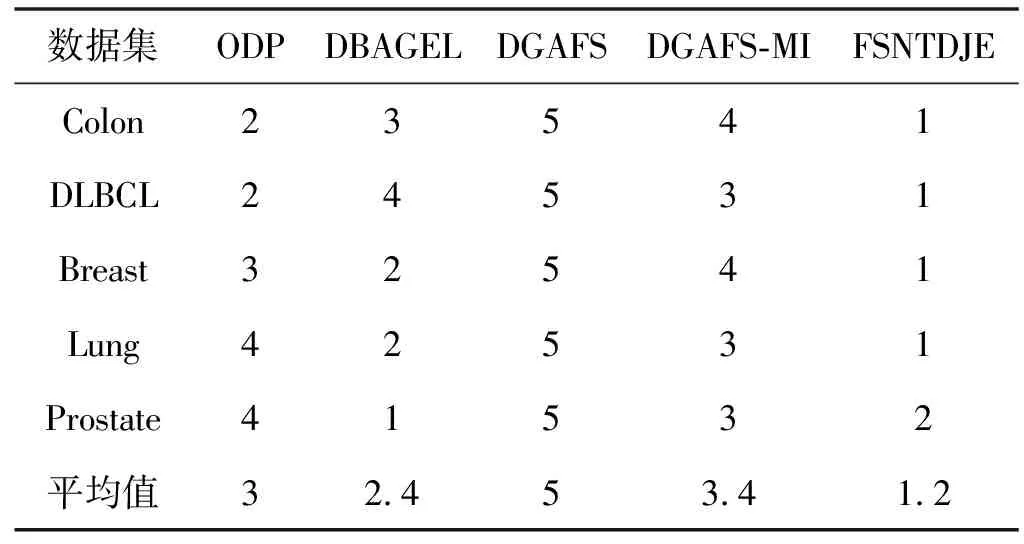
给出一个具有非空无限集U的不完备邻域决策系统INDS=〈U,C,D,δ〉,任意B⊆C和D={d},对于任意a∈B,提出一种称为邻域条件熵约简的不完备邻域决策系统的约简,如下:如果NTE(D|B)=NTE(D|C)和NTE(D|B-{a}) 式中:NTB(xi)和NTD(xi)分别是xi关于B和D的邻域容差类,NTD(xi)∈U/D。 命题8假设存在一个不完备邻域决策系统INDS=〈U,C,D,δ〉,并且有一个非空无限集U和B⊆C;当且仅当B是不完备邻域决策系统中C相对于D的邻域条件熵约简时,B是不完备邻域决策系统中C相对于D的邻域容差约简。 图1中显示了用于特征选择的数据分类过程,其中引入了Fisher评分方法以初步减少高维数据集的维数。为了支持有效的特征选择,将基于邻域容差依赖联合熵(FSNTDJE)的特征选择算法设计为算法1。 图1 用于数据分类的特征选择方法的处理流程 算法1FSNTDJE 输入:不完备邻域决策系统INDS=〈U,C,D,δ〉,邻域参数δ。 输出:最优属性子集B。 (1) 初始化B=∅,R=∅; (2) 计算:NTDE(C,D); (3) Fori=1 to |C| do (4) 计算Siginner(ci,C,D); (5) IfSiginner(ci,C,D)>0 (6)B=B∪{ci}; (7) End if (8) End for (9) 令R=C-B; (10) WhileNTDE(B,D)≠NTDE(C,D) (11) Forj=1 to |R| do (12) 计算NTDE(B∪{aj},D); (13) 选择aj使得满足max{aj∈R|NTDE(B∪{aj},D)},并且如果多个属性满足最大值。然后选择前者; (14) End For (15) 令B=B∪{aj},R=R-{aj},并计算NTDE(B,D); (16) End While (17) Fork=1 to |B| do (18) 选择一个bk∈B; (19) 计算NTDE(B-bk,D); (20) IfNTDE(B-bk,D)>NTDE(B,D) (21)B=B-bk; (22) End if (23) End (24) 返回最优属性子集B 计算邻域容差类的过程对特征选择的时间复杂度有很大影响。FSNTDJE的主要计算涉及两个重要方面:获得邻域容差类和计算邻域容差依赖联合熵。首先,为了进一步降低邻域容差类的计算时间复杂度,采用了排序算法。然后,邻域容差类的时间复杂度为O(mn),其中:m是样本数;n是特征数。同时,邻域容差依赖联合熵的计算时间复杂度为O(n)。由于O(n) 为了验证本文方法的分类性能,在15个公共数据集:7个UCI数据集(Nursery、Credit、Mushroom、Wpbc、Soybean、Annealing和Ozone level)和8个DNA微阵列基因表达数据集(Colon、DLBCL、Brain、Leukemia、Breast、Lung、MLL和Prostate)上获得了所有对比算法的综合结果并进行了分析。表1中详细描述了所有数据集。 表1 15个公共数据集的描述 实验是在一台运行Windows 10的计算机上进行的,该计算机具有3.20 GHz的Intel(R)i5 CPU和4.0 GB内存。所有仿真实验均在MATLAB 2016a中实现,并选择了4个分类器,包括Naive Bayes、C4.5、KNN和CART,以说明分类结果。10个数据子集中的每个子集仅被用作测试数据集一次。交叉验证重复10次,10个测试结果的平均值是所选特征的数量和分类精度。 实验的第二部分重点研究了不同邻域参数下的分类精度和约简率。为了解释不同邻域参数值的分类精度和约简性能,需要一个约简率来评估本文方法的特征冗余性能。 定义14数据集的约简率定义为: (14) 式中:|C|描述条件属性的数量;|R|表示在给定的邻域参数下生成的所选特征的数量。由于较高的约简率表明该方法对数据集的约简能力较强,因此较高的约简率意味着冗余度会降低。 对于8个高维基因表达数据集,采用Fisher评分方法,并基于8个数据集中的所有基因对其进行排序,然后选择g个基因形成候选基因子集。获取以下7个维度(10、50、100、200、300、400和500)下的分类精度,以便可以选择适当的维度进行特征选择。图2显示了8个基因表达数据集上分类精度和基因数量之间的变化趋势。可以看出,当基因数量增加时,精度通常会发生变化。因此,对于Colon和MLL数据集,可以将基因的维设置为200维特征,而对于DLBCL、Lung和Prostate数据集,可以设置为50维特征。对于Brain数据集,可以设置为400维特征。Leukemia和Breast数据集均可设置为100维特征。 注意,如果所有特征值都是分类的,则邻域容差关系将退化为容差关系。因此,在实验中,对于3个数据集(Nursery、Mushroom和Soybean),邻域参数将设置为0。通过使用具有不同邻域参数值的FSNTDJE算法获得十二个数据集上所选特征的分类精度。在获得具有不同参数的特征选择结果之后,对于4个UCI数据集,在Naive Bayes和C4.5分类器下实现了分类精度。对于8个基因表达数据集,在KNN(k=10)和C4.5分类器下评估分类精度和约简率。由于篇幅所限,仅展示Credit数据集在不同参数值下的结果,如图3所示,其中水平坐标代表间隔0.05时δ∈[0.05,1]的不同邻域参数值,左右垂直坐标分别表示精度和约简率。 图3 具有不同邻域参数值的12个数据集的分类精度和约简率 可以看出,不同的参数对FSNTDJE的分类性能有很大的影响。对于其他数据集,也显示了相类似的结果。因此,对于每个数据集,可以根据结果图选择约简率较高且能够保证两个分类器均能有较高分类准确度的参数。 对比算法包括:(1) 基于条件熵的粗糙集特征选择算法(FSCE)[6];(2) 基于正逼近的粗糙集不完备特征选择算法(IFSPA)[7];(3) 使用粗糙集模型的基于正区域的特征选择算法(FSPR)[8];(4) 基于粗糙集理论的启发式SetCover特征选择算法(SetCover)[9]。通过使用不同邻域参数,并且获得了表2的7个UCI数据集上所选特征的平均数量和适当的邻域参数,如表2所示。其中,从10倍交叉验证方法中获得了这5种方法的选定特征子集的平均大小。本文表中粗体字均表示最佳结果。 表2 5种算法选择的特征数 表2列出了5种不同算法使用10倍交叉验证选择的平均特征数。可以看出,使用Naive Bayes和C4.5分类器,在大多数情况下,FSNTDJE选择的平均特征数量少于FSCE、IFSPA、FSPR和SetCover。对于Nursery和Soybean数据集,在2个不同的分类器下,SetCover和FSNTDJE算法获得了几乎相同的平均特征数。但是,它们两者都比其他3种算法多大约一个。在Credit和Annealing数据集上,FSNTDJE选择的平均特征数略低于FSPR,并且在5种算法中均达到最小值。对于Mushroom数据集,FSNTDJE选择的平均特征数为4.2,比其他4种算法的平均特征数少0.2~3.4。对于Wpbc数据集,在Naive Bayes分类器下FSNTDJE的选定特征数为4.9,达到最低值。但是,在C4.5分类器下,FSNTDJE选择的平均特征数与Wpbc的SetCover算法几乎相同。在这两个分类器下,FSNTDJE达到了Ozone level数据集上最少特征数。此外,平均指数表示所有结果的平均值。显然,表2中Naive Bayes分类器下FSNTDJE的平均结果是最小的。总体而言,就所有数据集而言,所提出的FSNTDJE算法在所选特征的平均数量方面是有效的。 接下来,使用6种方法评估所选特征的分类性能,说明了本文方法的平均分类精度,即通过10倍交叉验证选择特征子集;此外,为了获得客观的分类结果并减少随机误差,将所有的比较方法进行10次,结果是10次分类精度评估的平均值。将FSNTDJE算法与以上4种特征选择方法(FSCE、IFSPA、FSPR和SetCover)以及原始数据处理方法(ODP)进行了比较。使用两个分类器(Naive Bayes和C4.5)测试分类性能。在Naive Bayes和C4.5分类器下通过6种方法选择的最佳特征的平均分类精度分别显示在表3和表4中。 表3 Naive Bayes分类器下6种方法的分类精度 表4 C4.5分类器下6种方法的分类精度 从表2中可以看出,在这5种算法选择的平均特征数上几乎没有差异,在此基础上,表3和表4显示了这6种方法之间的差异。显然,除了Naive Bayes分类器下的Wpbc和Soybean数据集,以及C4.5分类器下的Nursery、Mushroom和Annealing数据集之外,大多数数据集上的FSNTDJE算法的分类精度均优于其他5种方法。此外,在表3和表4中,FSNTDJE的平均精度得到了提高,且在2种不同的分类器上是最高的。从表3和表4可以看出,在Naive Bayes分类器下,虽然FSNTDJE在所选特征的平均大小上不如FSCE、IFSPA和FSPR,但是FSNTDJE的分类精度比Nursery数据集的ODP、FSCE、IFSPA和FSPR高0.024 0~0.052 2;但是,FSNTDJE在Soybean数据集上不如SetCover。尽管这5种算法选择的特征的平均大小存在一些差异,但是FSNTDJE的平均精度在所有数据集上均高于其他方法,除了Wpbc和Soybean数据集。同样,从表3和表4中可以看出,在C4.5分类器下,FSNTDJE的平均精度比其他5种方法高0.009 4~0.022 2,并且在所有数据集中,FSNTDJE的精度与SetCover的精度几乎相同。对于Mushroom数据集,FSNTDJE的分类精度比ODP、FSPR和SetCover低0.05。但与其他方法相比,FSNTDJE选择的特征较少,并且显示出比FSCE和IFSPA更好的分类性能。综上所述,就平均精度而言,FSNTDJE算法在Naive Bayes和C4.5中表现出了极大的稳定性,而ODP、FSPR和SetCover算法的精度则有些不稳定。从表3和表4的结果可以确定,对于Naive Bayes下的Nursery数据集,以及C4.5下的Mushroom和Annealing数据集,FSNTDJE可能会减少特征选择过程中的一些重要特征,结果降低所选特征子集的分类精度。 在进行实验的过程中,按时间复杂度对5种特征选择方法进行了粗略排序:O(FSNTDJE) 进一步根据所选特征的数量及其分类精度,说明FSNTDJE算法在所选数据集上的分类结果。这里,比较中使用的4种不完备数据集的最新特征选择方法包括:(1) 基于启发式可分辨矩阵的模糊粗糙集特征选择算法(DMFS)[10];(2) 基于粗糙集的向后属性约简算法(BKAR)[11];(3) 粗糙集中不完备决策系统的具有前向贪婪策略的基于互信息的特征选择算法(MIFS)[12];(4) 基于可分辨矩阵的优势粗糙集知识约简算法(DMKR)[13]。应当注意,为了将FSNTDJE算法与上述4种特征选择方法和ODP方法进行比较,从表1中选择了Credit和Annealing数据集。表5和表6显示了6种不同方法的实验结果,其中,在Naive Bayes和C4.5分类器下可以实现具有10倍交叉验证的所选特征的平均数量和10次评估的平均精度。 表5 6种方法对所选Credit特征的分类精度 表6 6种方法对所选Annealing特征的分类精度 如表5所示,FSNTDJE实现了所选的Credit特征数量最少,分类精度最高。与其他5种方法相比,该算法选择的平均特征数比5种方法要少2.0~4.5。另外无论哪种分类器,本文方法选择特征的精度均高于其他5种方法,即在Naive Bayes分类器下,该算法的精度比其他方法高0.052 2~0.089 8,在C4.5分类器下,比它们高0.020 0~0.089 2。因此,FSNTDJE算法可以为Credit数据集实现出色的分类性能。 根据表6的分类结果,FSNTDJE算法得到的Annealing特征选择数量最少、平均精度最高,并且该算法在Naive Bayes分类器下选择的特征精度与DMFS、BKAR和DMKR算法的相当,且分别比ODP和MIFS高0.325 9和0.078 5。此外,FSNTDJE的精度类似于MIFS,并且在C4.5分类器下高于其他4种方法的精度。因此,FSNTDJE算法可以从原始Annealing数据集中删除冗余特征。 从以上所有结果和分析中可以明显看出,对于不同的学习任务和分类器,没有一种算法始终比其他算法更好。通常,从表3至表6可以看出,与其他特征选择方法相比,FSNTDJE算法可以反映特征的决策能力,避免因离散化而导致有用信息的丢失,并解决了不完备邻域决策系统中的不确定性问题和有效提高分类性能。因此,在不完备的低维UCI数据集上,FSNTDJE算法优于其他相关的特征选择方法。 进一步展示了本文方法在高维基因表达数据集上的分类性能。将FSNTDJE算法与4种最新的特征选择方法进行了比较,包括:(1) 基于粗糙集的相关特征选择算法(CFS);(2) 基于快速相关的粗糙集滤波特征选择算法(FCBF);(3) 交互特征选择算法,它可以处理特征交互并有效地选择相关特征(INT);(4) 基于信息增益和散度的统计机器学习特征选择算法(IG)。从表1中选择了5个基因表达数据集,获得了使用10倍交叉验证和基因表达数据集上的适当邻域参数选择的特征子集的平均大小,结果如表7所示。 表7 5种算法选择的基因数量 表7显示了在Naive Bayes和C4.5分类器下使用10倍交叉验证通过5种特征选择算法选择的平均基因数。很明显,在大多数情况下,FSNTDJE算法优于CFS、FCBF和INT算法。但是,对于Brain数据集,FCBF提供了最佳结果,IG则选择了DLBCL数据集上的最佳基因数量。FSNTDJE算法为Naive Bayes分类器下的Colon和Prostate数据集选择最小平均基因。对于Breast数据集,在两个不同的分类器下,FSNTDJE选择的基因数量为7,并且达到最小值。此外,FSNTDJE选择的平均基因数是最好的,在两个不同的分类器上比IG分别平均低0.84和0.32。总而言之,所提出的方法可以为高维基因表达数据集选择最少的基因。 根据表7中的结果,使用Naive Bayes和C4.5分类器评估5个基因表达数据集的分类结果。使用3个指标来评估特征选择的分类性能,包括准确度(Acc)、真阳性率(TPR)和假阳性率(FPR)。TPR越高,FPR越低,该方法越好。3个指标的公式分别表示为: (15) (16) (17) 式中:TP表示检测为正确的阳性样本数;FP表示检测为错误的阳性样本数;TN表示诊断为正确的阴性实例数;FN表示诊断为错误的阴性实例数。表8和表9分别显示了在Naive Bayes和C4.5分类器下用6种方法选择的基因的Acc、TPR和FPR值。所有比较的方法都执行10次,并且将Acc的值评估为10次分类操作的平均值。 表8 Naive Bayes分类器下6种方法的3个指标 表9 C4.5分类器下6种方法的3个指标 从表7可知,5种算法在所选基因的平均数目上有很大的不同。根据表8和表9,除了Naive Bayes分类器下的Colon和Brain数据集和C4.5分类器下的Brain数据集之外,FSNTDJE的分类准确性优于其他5种方法。此外,FSNTDJE的TPR和FPR值在这5个数据集中的大多数上都取得了更好的结果。根据表8和表9,在Naive Bayes分类器下,明显可以识别出这6种方法之间的差异。尽管从DLBCL和Brain数据集中选择的平均基因而言,FSNTDJE的性能不如IG,但在Naive Bayes分类器中的Acc、TPR和FPR平均值最佳。对于Colon和Brain数据集,FSNTDJE的Acc分别比CFS和ODP的Acc低近0.018 8和0.015 8,这是因为FSNTDJE算法在约简过程中丢失了Colon和Brain数据集的一些重要基因,从而导致分类准确度降低。对于Breast数据集,FSNTDJE在平均基因数上达到最小,在3个指标上获得最佳结果。尽管在TPR中,FSNTDJE比Prostate数据集的CFS、FCBF和INT低约0.06,比Brain数据集的FCBF低约0.09,但Prostate和Brain数据集的FPR值最小。同样,从表8和表9可以看出,在C4.5分类器下,FSNTDJE的Acc平均值比其他五种方法的平均值高出0.082~0.304。与ODP的结果相比,除Prostate数据集外,本文方法的TPR有了显著提高。此外,关于FPR,对于DLBCL和Prostate数据集,FSNTDJE的FPR最低;但是,其平均值比ODP的平均值高出近0.064。根据表7、表8和表9中的结果,尽管FSNTDJE并未在DLBCL和Brain数据集中选择最少的基因,但FSNTDJE在大多数基因表达数据集中均达到了相对最佳的结果。总体而言,实验结果表明,本文方法可有效消除冗余基因并提高高维基因表达数据集上的Acc和TPR。 与先前对低维UCI数据集的时间复杂度分析相似,以上5种方法的比较说明了时间复杂度的大致顺序如下:O(FSNTDJE) 与FSNTDJE相比的4种最新方法描述如下:(1) 基于可分辨矩阵的模糊粗糙集约简算法(DMRA)[14];(2) 基于模糊正区域的粗糙集加速算法(FPRA)[15];(3) 基于模糊粗糙集的边界区域特征选择算法(FRFS)[16];(4) 基于直觉模糊正区域的模糊粗糙集基因选择算法(IFPR)[17]。类似于之前的实验方法,所有比较方法均运行10次,并且在KNN(k=10)和CART分类器下4个基因表达数据集的平均分类精度是10次评估的平均值。表10和表11分别显示了在KNN和CART分类器下这6种方法的分类精度。 表10 KNN分类器下6种方法的分类精度 表11 CART分类器下6种方法的分类精度 可以看出,除了KNN分类器下的Breast数据集和CART分类器下的MLL数据集,FSNTDJE算法的平均分类精度几乎在所有数据集上都优于其他5种方法,且FSNTDJE算法的平均分类精度最高。根据表10,在KNN分类器下,对于Colon、Leukemia和MLL数据集,FSNTDJE的分类精度最高,分别为0.876 3、0.901 9和0.961 5。但是,对于Breast数据集,FSNTDJE的精度略逊于DMRA的精度。如表11所示,在CART分类器下,FSNTDJE在几乎所有数据集上都达到了最高的精度。但是,对于MLL数据集,FSNTDJE的平均精度比IFPR低0.062,比其他4种方法高0.026 5~0.099 2。总体而言,就平均精度而言,FSNTDJE算法对KNN和CART分类器下的4个高维基因表达数据集表现出更强的稳定性,而DMRA、FPRA、FRFS和IFPR算法的分类性能略有不稳定。因此,可以证明FSNTDJE算法可以消除冗余基因,显著提高分类性能,并且优于高维基因表达数据集的其他5种相关特征选择方法。 为了进一步评估FSNTDJE算法的分类性能,与3种最新的特征选择方法相比。这些用于对比的特征选择方法包括:(1) 动态贝叶斯遗传特征选择算法,是通过在粗糙集中增强贝叶斯遗传算法的原理而设计的(DBAGEL)[18];(2) 基于动态遗传算法的特征选择方法,用于选择重要特征(DGAFS)[19];(3) 通过选择重要特征并推算缺失值来实现基于粗糙集的特征选择算法(DGAFS-MI)[20]。从表2中选择了5个基因表达数据集(Colon、DLBCL、Breast、Lung和Prostate),使用了Naive Bayes和KNN(k=10)分类器,表12和表13分别详细显示了在2种不同分类器下的5种不同特征选择方法的实验结果。 表12 Naive Bayes分类器下5种方法的分类精度 表13 KNN分类器下5种方法的分类精度 如表12所示,在Naive Bayes分类器下,除Prostate数据集外,FSNTDJE的分类精度明显优于其他4种方法,并且在5个基因表达数据集上,ODP、DBAGEL、DGAFS和DGAFS-MI算法的精度相似。在Prostate数据集上,FSNTDJE的精度比DBAGEL的精度低0.082 8,比其他3种方法的精度高0.005 4~0.170 7。这是因为当FSNTDJE处理基因数据集时,Prostate数据集仍然存在一些噪声,因此这种情况会降低精度。但是,FSNTDJE的平均精度比其他4种方法高0.056 3~0.165 4,并达到了最高值。从表13中可以看出,在KNN分类器下,FSNTDJE选择的基因子集的平均分类精度在Colon、DLBCL、Lung和Prostate数据集上是最好的。但是,对于Breast数据集,FSNTDJE的精度比DBAGEL的精度低0.035 7,比其他三种方法的精度高0.020 9~0.111 8。原因是FSNTDJE无法充分消除噪声基因,这会削弱所选Breast基因的分类性能。综上所述,FSNTDJE模型可以有效地减少高维基因表达数据集的维数,并在这些大规模和高维数据集上实现出色的分类性能。 为了证明特征选择结果的统计性能,采用了Friedman检验和Bonferroni-Dunn检验来进一步研究采用几种不同方法的每个分类器的分类精度。Friedman统计量表示为: (18) (19) 式中:s是方法数量;T是数据集数量;Ra是方法A在所有数据集中的平均排名。FF遵循具有s-1和(s-1)·(T-1)自由度的Fisher分布。如果在Friedman检验后否定了原假设,则可以引入Bonferroni-Dunn检验以进一步检测统计意义上哪些算法不同。如果平均距离水平超过临界距离,则两种算法将有显著差异。临界距离表示为: (20) 式中:qα是检验的临界列表值;α是Bonferroni-Dunn检验的显著性水平。 对于表3和表4中的7个低维UCI数据集,将FSNTDJE算法与5种方法:ODP、FSCE、IFSPA、FSPR和SetCover进行比较,以进行Friedman统计。开发了2个Friedman检验来调查这6种特征选择算法的分类性能是否存在显著差异。从表4和表5中获得的分类精度来看,在Naive Bayes和C4.5分类器下的6种算法的排名结果分别显示在表14和表15中。 表14 Naive Bayes分类器下6种算法的排名 表15 C4.5分类器下6种算法的排名 表16 两个分类器下6种方法的排名 表17 Naive Bayes分类器下6种特征选择方法的排名 以下部分致力于所有高维基因表达数据集的统计分析。根据表8和表9的分类结果,在Naive Bayes和C4.5分类器下的6种特征选择方法的排名结果显示在表17和表18中。 表18 C4.5分类器下6种特征选择方法的排名 表19 KNN分类器下6种方法的排名 表20 CART分类器下6种方法的排名 表21 Naive Bayes分类器下5种方法的排名 表22 KNN分类器下5种方法的排名 为了能够处理混合数据集和不完全数据集,并能同时保持原始分类信息,提出一种基于Lebesgue和熵度量的不完备邻域决策系统特征选择方法。通过高维与低维多个数据集实验可以得出如下结论: (1) 针对低维数据集,FSNTDJE算法实现了较低的时间复杂度,可以有效地消除冗余特征并优化不完备数据集的分类性能。 (2) 针对高维数据集,FSNTDJE算法可以消除冗余基因,有效地减少高维基因表达数据集的维数,并在这些大规模和高维数据集上实现出色的分类性能。 (3) FSNTDJE算法可以反映特征的决策能力,避免因离散化而导致有用信息的丢失,并解决了不完备邻域决策系统中的不确定性问题和有效提高分类性能。 (4) 统计数据进一步表明了本文方法相对于其他方法,能够更加有效地处理混合数据集和不完全数据集,并保持较好的分类性能。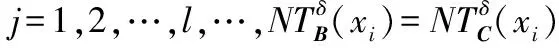
2.3 特征选择算法

3 实验与结果分析
3.1 实验准备
3.2 不同邻域参数值的影响
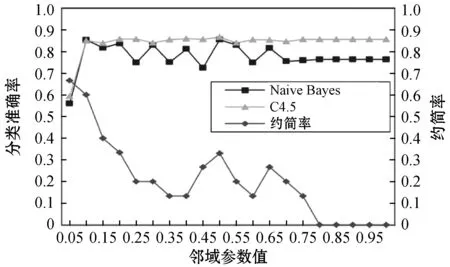
3.3 低维UCI数据集的分类结果
3.4 高维基因表达数据集的分类结果
3.5 统计分析
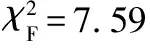
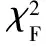
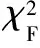
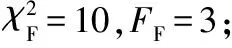
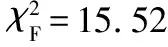
4 结 语

