过程挖掘中增强活动依赖的最优对齐算法
邵叱风 方贤文 杨慧慧
(安徽理工大学数学与大数据学院 安徽 淮南 232001)
0 引 言
BPM(Business Process Management)业务流程管理[1-2]伴随着大数据时代的到来得到了进一步发展。从业务流程出发,基于信息及管理技术提供统一的建模、运行和监控环境。经过业务流程的不断执行,信息系统将生成大量的事件日志文件[3],其记录了与流程密切相关可用于进一步业务流程分析的重要数据,因此,流程挖掘对提高业务流程管理水平而言受到人们越来越多的重视[4-7]。在企业管理中,完整的信息管理系统要求流程模型和事件日志之间具有很高的重构性,即希望模型的过程行为和性质可以从完整描述的日志中表现出来[8]。然而,通过比较模型和事件日志可知,信息系统中记录的事件日志与基于业务流程构建的模型之间总是存在一些偏差,因而使得日志中的部分行为无法在模型上重放[9-10]。针对上述问题,对过程模型与记录系统实际运作的事件日志之间进行一致性校验变得至关重要[11]。
近年来,校验给定模型和事件日志之间一致性的多种方法已被提出[4-5,12-19],其中文献[16]所做的对齐方法是最先进的方法之一。文献[17]将日志与模型进行对齐,提出一个复杂的方法用以指出偏差发生的位置及偏差程度;文献[18]分析那些最优对齐包含的移动集合完全相同,只是移动出现顺序不同,继而提出相似最优对齐的概念;一般而言能够检测到最小偏差成本的一组对齐被认为是事件日志与业务流程之间的最优对齐[19]。使用现有方法可以得到事件日志中的迹与Petri网的发生序列之间的所有最优对齐。对齐处理与偏差检测作为很多研究工作的重要组成部分,因而在过程挖掘领域中越来越重要,例如,模型修复[20-22]和遗传优化过程挖掘[23]等。
现有的最优对齐方法在计算对齐成本时大多仅考虑对齐中的移动个数(包括相似性最优对齐),缺乏对单一活动成本即活动依赖的考虑。在此提出一种基于依赖增强的最优对齐计算方法,目的提高计算序列对齐的效率、最优对齐对活动的依赖性。基于自定义得分矩阵的配置,使用动态规划的方法计算日志中所有序列与模型可观测迹的对齐;分析对齐集合中移动的信息,通过加权的方式计算模型与日志上合法移动的总成本;最后利用分组排序得到日志与模型的最优对齐序列及对齐成本。
1 基本概念
本节内容列出了文章所需的部分基本概念,用以辅助文章的阅读。Petri网相关定义参考文献[24]。
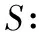
1)Move(x,y)是一个日志迹上的移动,当且仅当x∈且y=→。
2)Move(x,y)是一个系统上的移动,当且仅当x=→且y∈T。
3)Move(x,y)是一个同步移动,当且仅当x∈,y∈T且λ(y)=x。
定义2(对齐) 迹υ∈*和网系统=(N,Mini,Mfin),其中=(P,T,F,λ)上的执行σ之间的对齐是拥有S上合法移动的有限序列其中π1(γ)|=υ且π2(γ)|T=σ。
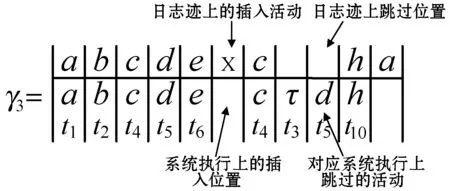
例如,γ1和γ2展示了指定两个域的两个序列的移动分别为<(a,t1),(c,t4),(b,t2),(d,t5),(→,t7),(f,t8),(g,t9),(→,t11)>和<(a,t1),(c,t4),(b,t2),(d,t5),(→,t5),(→,t4),(→,t3),(→,t5),(→,t7),(f,t8),(g,t9),(→,t11)>,并且π1(γ1)|=
定义3(对齐成本) 网系统S上的合法移动成本可表示为一个函数c:MS→N0,将成本分配到S上的合法移动。故迹υ∈*和网系统=(N,Mini,Mfin),其中=(P,T,F,λ)上的执行σ之间的对齐γ对应成本依据合法移动成本函数c,以及γ上所有的移动成本总和定义为:
(1)

即日志迹υ与模型中可观测迹的对齐成本最小的对齐为最优对齐,可能有多个最优对齐。比如两个对齐均插入或跳过一个活动,为体现日志与网系统中变迁的重要程度,降低最优对齐个数。下面给出定义5和定义6如下:
定义5(标签加权) 依据活动不同重要性,考虑单一活动成本,对对齐序列中的标签γi进行加权处理,对于权函数w:
w(π1(γi)|)=w(π2(γi)|T)=w(γi),w(γi)∈N
在输入过程中,输入形式如下:
Weightactivity:(A1,w(A1),A2,w(A2),…,Ai,w(Ai)),A=(∪{τ})*
定义6(移动加权) 依据偏差出现位置,考虑其对对齐成本的影响,在计算总的对齐成本时对于系统上的合法移动,迹上的合法移动按类别Weightskip、Weightinsert进行加权处理。输入形式如下:
Weightskip/Weightinsert:
(Costskip,W(Costskip),Costinsert,W(Costinsert))
Costtotal=Costskip×W(Costskip)+Costinsert×W(Costinsert)
(2)
则:
(3)

(4)
通过对活动的加权区分了对其中不同活动的成本;对偏差类别的加权区分了偏差发生位置的重要程度;相较于单一量化偏差个数的对齐成本求解进行了改进。
2 算法及其实现
此部分主要介绍基于动态规划求解两个序列的对齐,通过循环调用求得υ∈*和网系统=(N,Mini,Mfin),其中=(P,T,F,λ)上的执行σ的对齐;然后利用加权函数w对每个对齐的成本c(γ)进行计算,并按照日志的大小分成L.Size()组进行排序,求得日志迹与模型的最优对齐
2.1 序列对齐
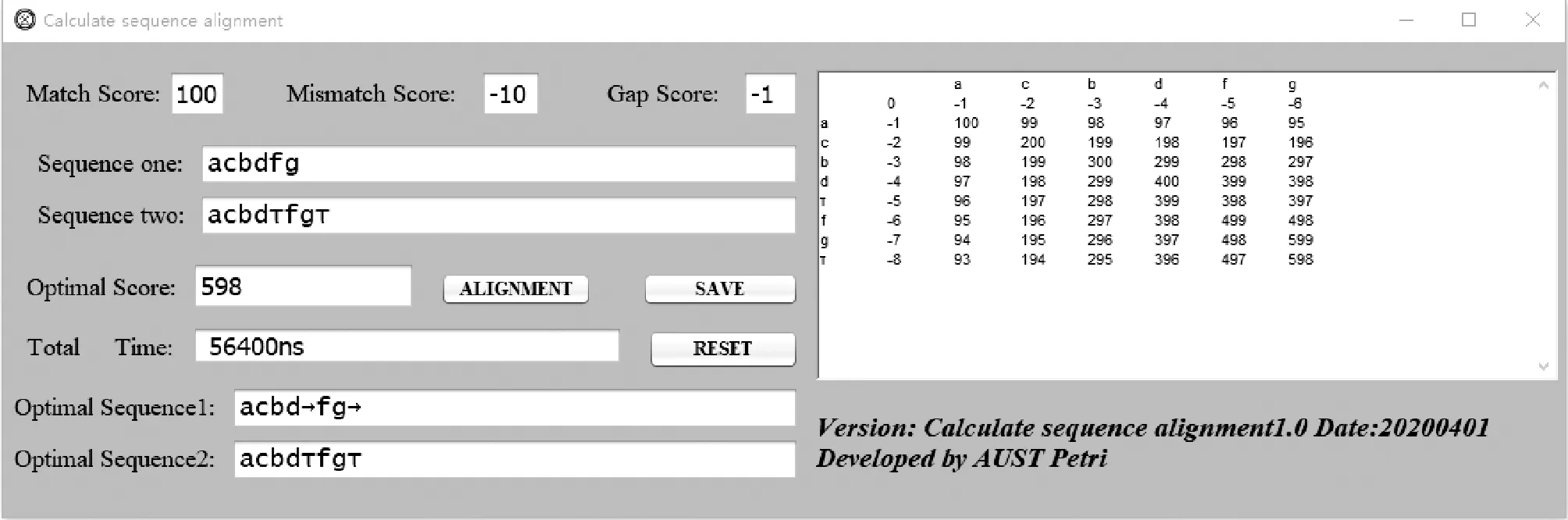
基于动态规划计算日志迹与模型可观测序列的对齐,主要是构建日志迹与模型可观测序列的打分矩阵,并回溯出得分最高的对齐结果。其中参数包括打分矩阵中的匹配得分、不匹配得分及间隙罚值,即同步移动、错误对齐及合法移动的分值。方法有以下几个主要步骤:
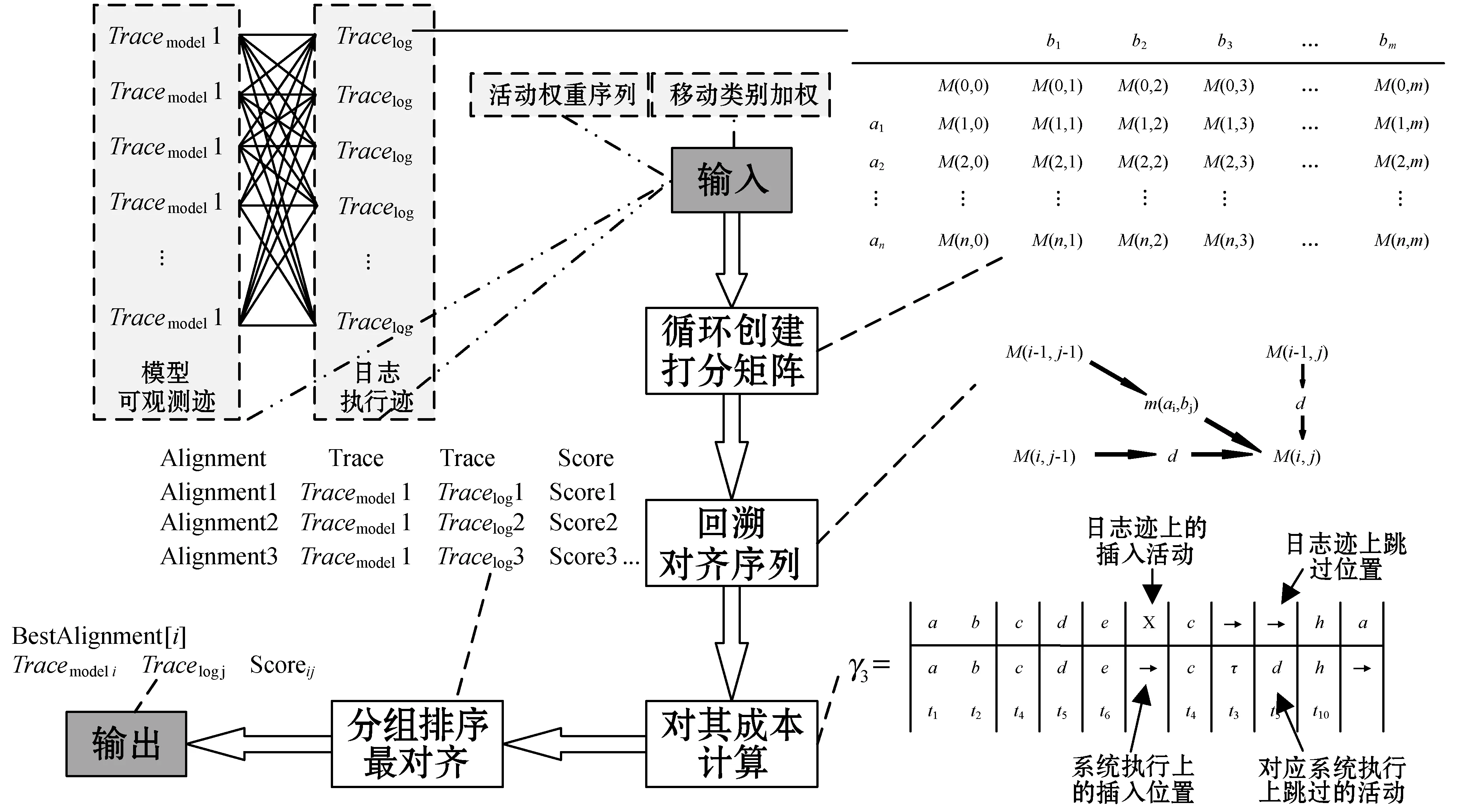
1) 矩阵初始化。对于日志迹υ=a1,a2,…,an和模型可观测序列σ=b1,b2,…,bm,然后创建大小为(n+1)×(m+1)的打分矩阵,其中:n为行数且是当前日志迹υ的长度;m是列数且是当前模型可观测序列σ的长度。然后用间隙罚值填充值矩阵的第一行和第一列。间隙惩罚是将对齐中未匹配字符与空白字符(间隙)进行比较时获得的值。
序列A和序列B的打分矩阵如图3所示。
2) 矩阵填充。假设打分矩阵称为矩阵M,则矩阵M的元素的公式为:
(5)
式中:M(i-1,j-1)为矩阵元素M(i,j)对角线左上角;M(i,j-1)为M(i,j)的左侧;M(i-1,j)为M(i,j)的上方;m(ai,bj)为序列a中的残基i和序列b中的残基j的残差矩阵;d为间隙惩罚的符号。假设间合法移动模型s(→,a)=s(a,→)=-d对于a∈Q,d>0,那么长度为L的间隙区域的值等于-dL。
假设合法移动分数是d,那么s(0,j)=-j×d,s(i,0)=-i×d,s(0,0)=0。
(6)
部分打分矩阵代码如Code_1和Code_2所示。
Code_1:Calculate the first row and first column of matrix according to gapvalue
1 private voidInitScore(intGap,intX,intY) {
2SCORE[0][0]=0;
3for(inti=1;i<=X;i++) {
4SCORE[i][0]=SCORE[i-1][0]+Gap;
5 }
6for(intj=1;j<=Y;j++) {
7SCORE[0][j]=SCORE[0][j-1]+Gap;
8 }
9 }
Code_2:Calculatethescorematrixaccordingtotheinterfaceinput
1privatevoidCalcScore(intMatch,intMiss,intGap,intX,intY,
2StringstringX,StringstringY) {
3intdiag,up,left;
4for(intj=1;j<=Y;j++) {
5for(inti=1;i<=X;i++) {
6diag=Diag(Match,Miss,i,j,stringX,stringY);
7up=Up(Gap,i,j);
8left=Left(Gap,i,j);
9if(diag>=up&&diag>=left) {
10SCORE[i][j]=diag;
11DIRECTION[i][j]=′D′;
12 }elseif(up>=left) {
13SCORE[i][j]=up;
14DIRECTION[i][j]=′U′;
15 }else{
16SCORE[i][j]=left;
17DIRECTION[i][j]=′L′;
18 }
19 }
20 }
21 }
Code_1依据合法移动分值计算打分矩阵首行首列,Gap、X、Y分别为间隙罚值、序列X的长度、序列Y的长度。Code_1(2)对打分矩阵[0,0]位置元素赋值为0,Code_1(3-5)对首列除[0,0]位置外元素依据间隙罚值进行赋值处理,Code_1(6-8)对首行除[0,0]位置外元素依据间隙罚值进行赋值处理。
Code_2依据错误对齐、同步移动、合法移动计算首行首列外的打分矩阵及方向矩阵,Match(合法移动得分)、Miss(错误对齐得分)、Gap(间隙罚值得分)、X(序列X的长度)、Y(序列Y的长度)、StringX(序列X)、StringY(序列Y),Diag()、Up()、Left()为分值计算函数。Code_2(3-19)使用两层嵌套对打分矩阵首行首列外的位置元素进行赋值。
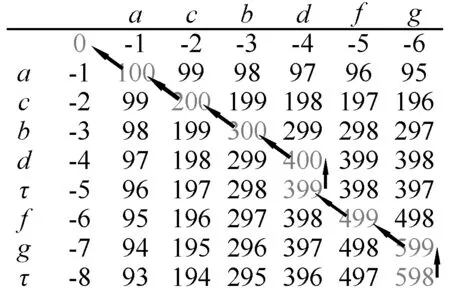
3) 回溯步骤。在完全填充大小为(n+1)×(m+1)的打分矩阵之后,对齐得分(所有替换值之和加上所有间隔惩罚之和)是两个序列的打分矩阵最右下角元素的值,M(n+1,m+1)=m(n,m)。回溯步骤如图4所示。
从起点M(n,m)开始回溯到终点m(0,0)。如果M(i,j)=M(i-1,j-1)+m(ai,bj),那么回溯轨迹为(i,j)→(i-1,j-1)。
4) 确定对齐结果。若回溯到左上角单元格,将ai添加到匹配字串A(即日志迹),将bj添加到匹配字串B(即模型可观测序列)。
若回溯到上边单元格,将ai添加到匹配字串A,将→添加到匹配字串B。
若回溯到左边单元格,将→添加到匹配字串A,将bj添加到匹配字串B。
部分回溯代码及界面右侧矩阵输出代码如Code_3和Code_4所示。
Code_3:Backtracking matrix output stringX
1 privateStringPrintOptimalX(StringStringX,StringOptimalX,inti,intj) {
2if(i==0&&j==0) {
3returnOptimalX;
4 }
5if(DIRECTION[i][j]==′D′) {
6OptimalX=PrintOptimalX(StringX,OptimalX,i-1,j-1);
7OptimalX=OptimalX+StringX.charAt(i-1);
8 }elseif(DIRECTION[i][j]==′L′‖j==0) {
9OptimalX=PrintOptimalX(StringX,OptimalX,i-1,j);
10OptimalX=OptimalX+StringX.charAt(i-1);
11 }else{
12OptimalX=PrintOptimalX(StringX,OptimalX,i,j-1);
13OptimalX=OptimalX+′→′;
14 }
15returnOptimalX;
16 }
Code_4:Backtracking matrix output stringY
1privateStringPrintOptimalY(StringStringY,StringOptimalY,inti,intj) {
2if(i==0&&j==0) {
3returnOptimalY;
4 }
5if(DIRECTION[i][j]== ′D′) {
6OptimalY=PrintOptimalY(StringY,OptimalY,i-1,j-1);
7OptimalY=OptimalY+StringY.charAt(j-1);
8 }elseif(DIRECTION[i][j]==′U′‖i==0) {
9OptimalY=PrintOptimalY(StringY,OptimalY,i,j-1);
10OptimalY=OptimalY+StringY.charAt(j-1);
11 }else{
12OptimalY=PrintOptimalY(StringY,OptimalY,i-1,j);
13OptimalY=OptimalY+′→′;
14 }
15returnOptimalY;
16 }
Code_3用于回溯出对齐序列X,StringX(对齐序列X)、OptimalX(对齐后序列X),i、j为元素在矩阵中的位置,依据确认对齐结果中的描述进行OptimalX的拼接,Code_4同理回溯对齐后序列Y。
计算单条日志迹与单条模型可观测序列对齐的方法通过Java编程实现,通过设定MatchScore(同步移动)、MismatchScore(错误对齐)、GapScore(合法移动)三个预值,并输入需要对齐的两个序列,点击ALIGNMENT按钮即可计算得出两对序列之间的最优对齐,并输出得分、运行耗时,且在界面右侧打印序对齐计算时生成的打分矩阵。SAVE按钮功能可将计算结果进行.txt或.rtf格式的保存。
插件进行日志迹
2.2 对齐成本
使用常规成本计算方法在计算日志与模型的最优对齐时,大多仅考虑对齐中的移动个数,一条日志迹可能与多个模型可观测迹形成最优对齐。在实际系统中,每个活动的重要程度必然不是完全相等的,且日志上移动与模型上移动的成本在模型修复时显然也是不等的。在此使用加权函数w加权计算对齐成本c(γ),考虑对齐计算时不同活动的权重、插入及跳过的权重,增加对齐计算时需考虑的因素,增加对齐成本计算结果对活动的依赖性,差异化具有相同移动个数且包含不同活动的对齐序列的成本。加权计算如图7所示。
加权计算对齐成本具体方法如Code_5所示,展示calculateCost函数进行对齐序列计算及其加权成本计算,tWeightstr(标签加权字符串)、logSEQstr(对齐后的日志序列)、modelSEQstr(对齐后的模型可观测迹)、MatchValue(同步移动分值)、MisMatchValue(错误对齐分值)、GapValue(合法移动分值)、weightofskip(跳过操作的权值)、weightofinsert(插入操作的权值),getAlignment()是对序列匹配的重复调用求解日志与模型的对齐序列,getCharacterPosition()获取移动的位置,getPositionCharacter()获取移动中包含的活动。
Code_5:Weighted calculation of alignment costs
1 publicList
2StringMismatchValue,StringGapValue,StringWeightofskip,StringWeightofinsert) {
3HashMap
4String[]logseq=logSEQStr.split(" ");
5String[]modelseq=modelSEQStr.split(" ");
6List
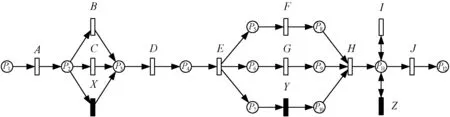
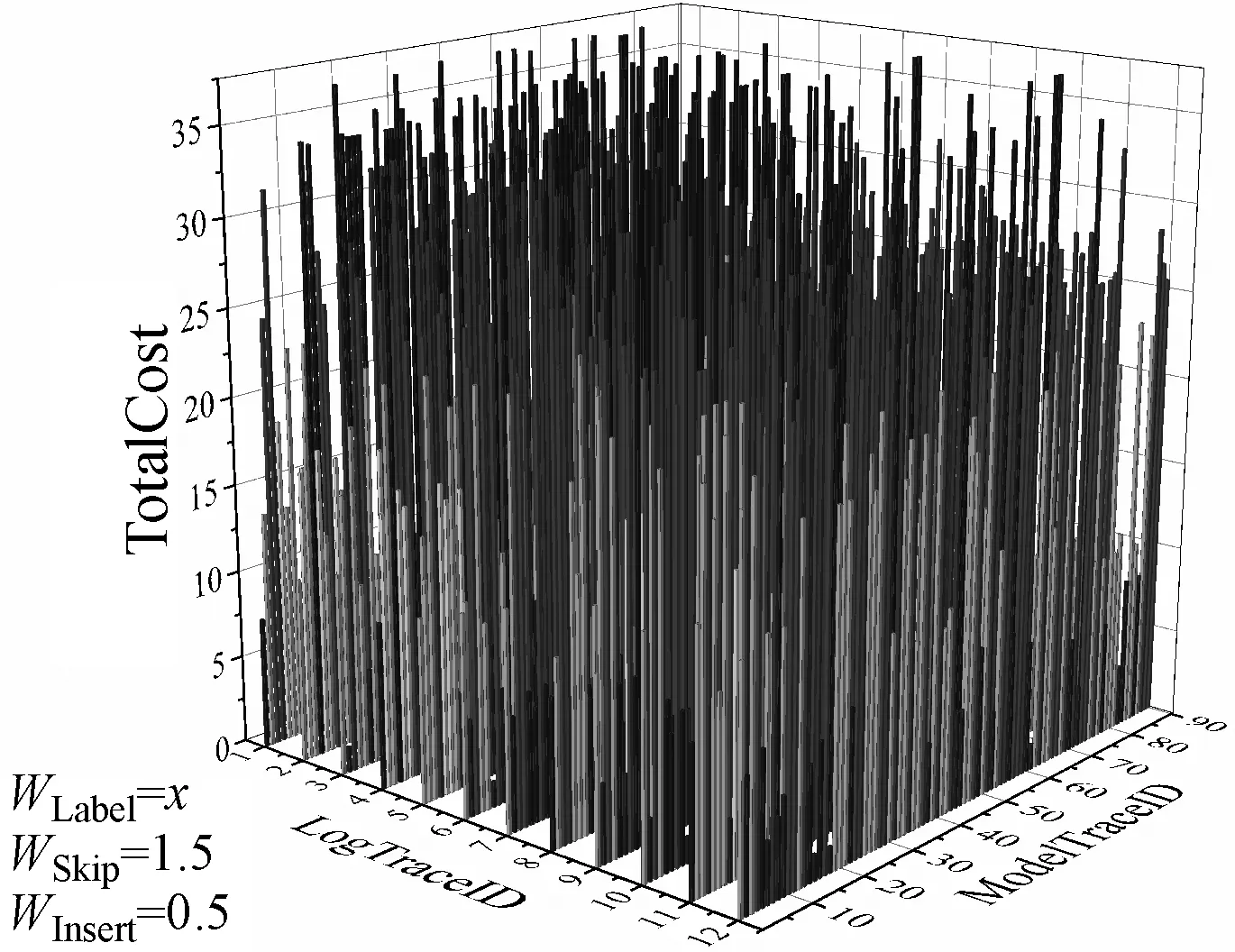
7for(intj=0;j 8Doubleskipscore=0.00,insertscore=0.00; 9if(result.get(j).getLogResult().contains("→")) { 10List 11List 12skipscore=addWeightScore(tWeight,Modelstr); 13result.get(j).setSkipCost(skipscore); 14result.get(j).setLogIndex(Logindex); 15result.get(j).setModelStr(Modelstr); 16 } 17if(result.get(j).getModelResult().contains("→")) { 18List 19List 20insertscore=addWeightScore(tWeight,Logstr); 21result.get(j).setInsertCost(insertscore); 22result.get(j).setModelIndex(Modelindex); 23result.get(j).setLogStr(Logstr); 24 } 25BigDecimalb1=newBigDecimal(Double.toString(skipscore)),b2=newBigDecimal(Double.toString(insertscore)); 26BigDecimalb3=getWeightOfKind(Weightofskip),b4=getWeightOfKind(Weightofinsert); 27result.get(j).setTotalCost(Double.parseDouble(b1.multiply(b3).add(b2.multiply(b4)).toString())); 28 } 29returnresult; 30 } 1) 在2.1节的基础上实现序列对齐方法的循环调用,Code_5(4-6)计算日志L中每条迹与模型S的所有可观测序列的对齐。 2) 依据定义5的输入形式,Code_5(3)初始化活动权值Map。 3) Code_5(7-28)为加权计算对齐成本部分,其中Code_5(9-16)统计日志迹上的跳过位置以及对应系统执行上跳过的活动并赋值给对象result;Code_5(17-24)统计系统执行上的插入位置以及日志迹上的插入活动并赋值给对象result。 4) 依据定义5的标签权值,定义6的移动类别权值,Code_5(25-27)计算对齐成本c(γ)。 5) 将对齐成本计算结果按模型可观测序列的条数等分为多组(Code_6),并排序得到每条日志迹的最优对齐。 Code_6用于对齐结果的分组,list为日志与模型的对齐结果,groupSize为分组大小,Code_6(2-4)用于计算分组数,Code_6(5-9)用于分组结果newList的赋值。分类加权计算对齐成本的方法由Java编程实现如图8所示。 Code_6:splite result 1 private staticList 2groupSize) { 3intlength=list.size(); 4intnum=(length+groupSize-1)/groupSize; 5List 6for(inti=0;i 7intfromIndex=i*groupSize; 8inttoIndex=(i+1)*groupSize 9newList.add(list.subList(fromIndex,toIndex)); 10 } 11returnnewList; 12 } 本节主要对动态规划序列对齐方法、对齐成本加权计算方法进行验证,分析序列对齐方法的耗时,不同权重对最优对齐结果的影响。实验选取如图9所示模型,该模型包含选择、并发和循环结构,以及静默变迁X、Y、Z。选取日志序列如表1所示。所有的实验均在配有I5-7300HQ 2.5 GHz四核处理器和16 GB运存的机器上进行的,使用Java SE 1.7开发环境。 表1 部分运行日志 Petri网模型常见的结构关系包括并发、选择和循环等[24],为增加执行序列的多样性及产生带有偏差的日志,选取如图9所示模型,包含静默变迁X、Y和Z,分布在选择、并发和循环结构中。对文献[25]中增广Petri网模型模拟运行插件进行改进,并对图9模型进行日志生成,为防止状态爆炸,模型中循环执行的次数限定为1,部分生成日志如表1所示。 为对动态规划求解耗时情况进行分析,在此取长度5∶5∶40的序列进行对齐,对齐耗时结果如图10所示。对齐计算的耗时与序列长度成正比,主要耗时为打分矩阵的构建(算法复杂度为O(mn))与序列对齐结果的回溯(时间复杂度为O(m+n))。 图1 同一序列的两个不同对齐 图2 增强活动依赖的最优对齐算法实现流程 图3 序列A和序列B的打分矩阵 图4 回溯步骤 图5 对齐序列计算界面 图6 打分矩阵及回溯过程 图7 加权计算示意图 图8 加权计算对齐成本求解最优对齐 图9 含有选择、并发和循环结构的模型 图10 不同长度序列对齐计算耗时 对于加权计算对齐成本方法的可行性,利用表1所示的日志与图9所示网系统进行对齐,并计算对齐成本(活动成本分别为默认1和(A,1,B,2,C,2,X,4,D,1,E,1,F,1,G,1,Y,1,H,1,I,6,Z,12,J,1)两种),插入及跳过成本权重设置为默认1和(WSkip=1.5,WInsert=0.5),对齐成本计算结果如图11所示,方法是可行的。 (a) 图12展示了不同标签取值对CostSkip、CostInsert的影响,WeightSkip、WeightInsert的设定增加了对齐成本线图的可区分度。图13中的线为对齐不同可观测迹的对齐总成本,非重叠处即出现了不同权值设置标签的插入或跳过。 图12 设置不同标签权重ADEFGHJ与模型可观测迹的对齐成本 图13 不同标签权重对ADEFGHJ最优对齐的影响 表2与表3展示了日志序列 表2 标签权值序列为x1时最优对齐序列 表3 标签权值序列为x2时最优对齐序列 x1=A,1,B,2,C,3,X,4,D,1,E,1,F,1,G,1,Y,1,H,1,I,6,Z,12,J,1x2=A,1,B,2,C,2,X,4,D,1,E,1,F,1,G,1,Y,1,H,1,I,6,Z,12,J,1 本文认为一致性检验在信息管理系统中发挥着越来越重要的作用,其中对齐是最先进、最全面的方法之一,且最优对齐被广泛使用。现有的最优对齐计算缺乏对活动依赖的考虑,继而在此提出一种新的方法,用于计算Petri网模型和日志迹之间的最优对齐。首先基于动态规划求解对齐(时间复杂度O(mn+m+n)),然后对于对齐结果依据自定义的活动权重及插入、跳过成本的权重计算对齐成本(时间复杂度O(mn)),最后对计算结果分组排序得出模型与日志迹之间的每一对最优对齐。实验结果表明动态规划求解对齐、加权计算对齐成本的方法是可行的,且最优对齐的求解方法在一定程度上体现了不同活动的重要性,增加了最优对齐对活动的依赖性,且降低了日志迹与模型之间相同最优对齐成本的个数,对原有的单一量化对齐成本求解进行了改进。 依据实验结果分析,未来工作可从以下几个方面展开:(1) 利用BPIC的真实数据和模型对方法进行测试和验证;(2) 改进加权计算对齐成本的方法,将其与对齐的求解相结合;(3) 在求解所有对齐、排序最优对齐时加入多线程的使用提高计算效率;(4) 加权计算后得到的对齐成本是不同的,进一步分析其对一致性检验的影响。3 实验分析

3.1 对齐耗时
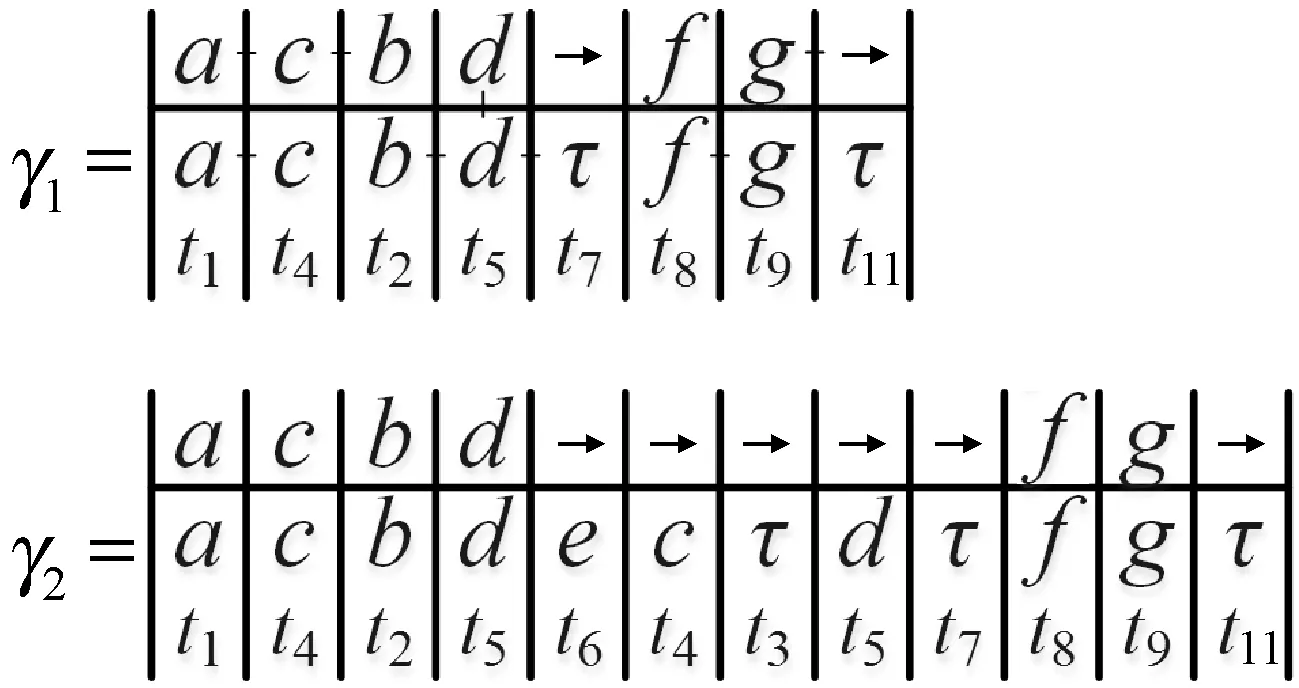
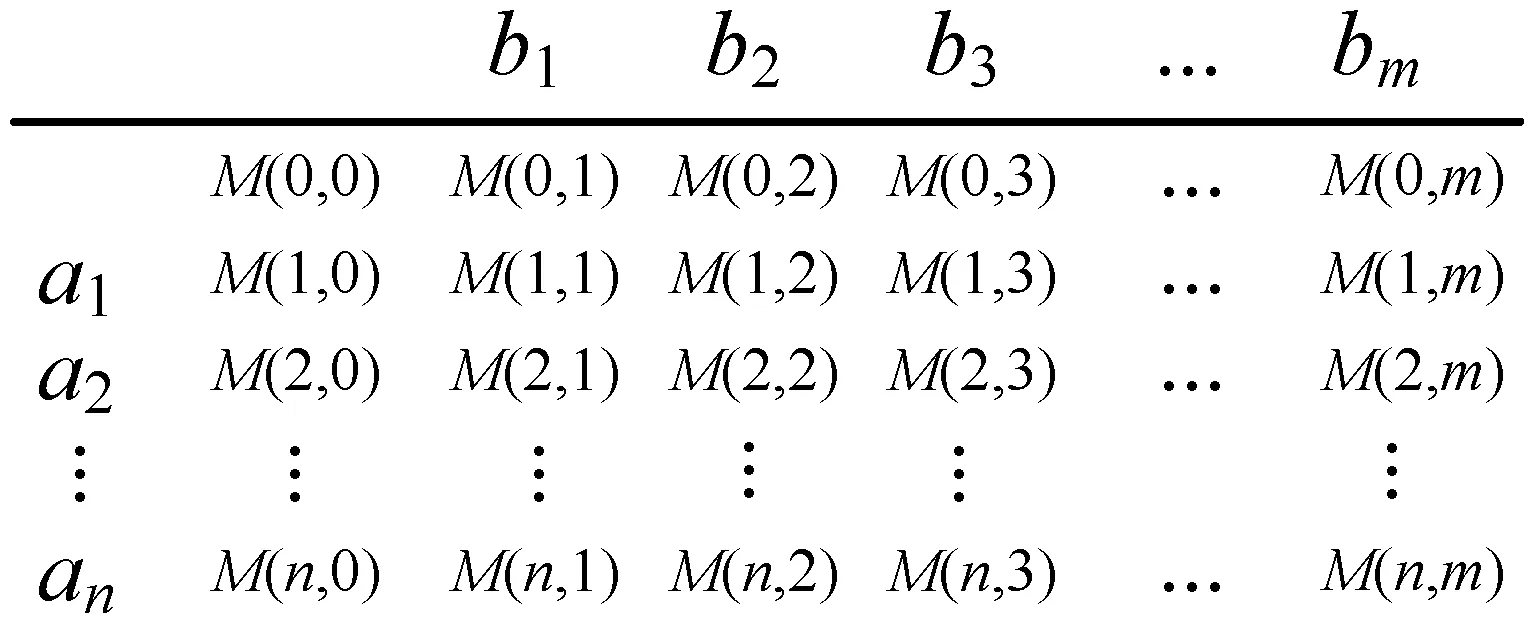
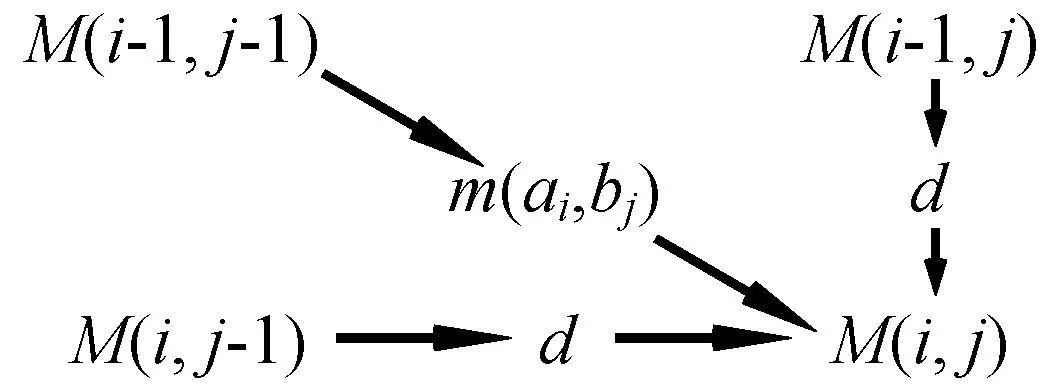


3.2 可行性及有效性




4 结 语

