OFDM系统中的窄带干扰信号检测算法研究

杨靖文 李迟生 杜 燕 王新民

(南昌大学信息工程学院 江西 南昌 330031)

0 引 言

基于OFDM系统的干扰检测是对系统内是否存在干扰进行检测。算法主要分为时域检测法与频域检测法。频域门限法由于其实现简单、检测准确度高等优点获得了广泛的应用[1]。文献[2]通过计算得到接收信号频域中的均值和标准差信息,再乘以设定的门限参数来设定门限值,来进行判决。这种基于均值和标准差的门限法比较灵活,且实现相对简单,但此方法在进行干扰检测时的漏检率较高。文献[3]中的CME算法和文献[4]中的FCME算法都是常用的干扰信号检测算法,FCME算法的检测性能较好,由于包含排序算法,导致在复杂度上相对于CME算法较高。但FCME算法在干扰因子在0.6以上时明显优于CME算法[5],即CME算法在干扰因子较低时,算法的检测性能较好,但随着干扰因子增长至0.6及以上时,检测率低于FCME算法。文献[6]中提出的分段CME算法(CME_B算法)首先将信号的所有频点幅度值分段,再取均值最小的一段,作为未受干扰的信号集,以此计算初始门限值来进行迭代,在不进行排序、降低算法复杂度的前提下,算法的检测性能接近FCME,且好于CME算法。文献[7-8]中的双门限法计算复杂度高,在应对窄带干扰时没有太大的优势[8],因此暂不考虑。但文献[6]中的分段CME算法中只考虑了分段数较多,取得的最小均值分段信号频谱幅度值均未受干扰影响的理想情况下,当分段数较低时,特别是所取分段中频点幅值受干扰影响时,检测性能就会下降,如果对最小均值分段中的信号进行过滤筛选,将受干扰的频谱幅值去除,则通过筛选后的最小均值分段生成的门限值会更有效地检测出干扰。

1 干扰系统模型

1.1 干扰信号模型

干扰信号检测通常是军事抗干扰的前提,当蓄意地发送干扰信号时,会影响通信质量,甚至中断通信。干扰检测作为干扰监测的前期工作,只有完成干扰信号的存在性检测才能进行识别、测向和干扰源定位等干扰监测工作[7]。其中,单音、多音、部分带宽干扰等是OFDM系统中常见的干扰形式。

1) 单音干扰(Single Tone Jamming,STJ)。单音干扰也叫点频干扰,其原理是产生一个频率接近载频的单频信号对通信系统实施干扰[8]。其时域表达式为:

i(t)=A0exp(2πf0t+θ0)

(1)

式中:A0、f0、θ0为干扰信号的幅度值、频率、初始相位。其中干扰频率f0与信号的子载波间隔Δf的关系可表示如下:

f0=(m+a)Δf

(2)

Δf=fs/N

(3)

式中:m和a分别为整数因子和分数因子,又称正交因子和频偏因子,表示相对于子载波m的相对频率偏移;fs为采样频率;N为FFT点的个数。

2) 多音干扰(Multi-Tone Interference,MTJ)。多音干扰相当于多个单音干扰的叠加,同时发送一定数量的频率,功率值不同的单音信号组合而成的干扰就是多音干扰,可以在同一时刻干扰多个频点上的信号。其时域表达式如下:

(4)

式中:L为单音干扰信号的数量,当L=1时即为单音干扰;Ai、fi、θi为不同干扰信号即第i个的单音干扰信号的幅度值、干扰频率、初始相位。

3) 部分带宽干扰(Partial Bandwidth Interference,PBJ)。部分带宽干扰是指有选择地干扰部分系统带宽[9],即对接收信号的某一部分带宽进行干扰。

1.2 干扰信号接收模型

有用信号s(t)经过发射端发出后,会受到干扰信号i(t)和噪声信号n(t)的影响,到达接收端后的信号为r(t)。得到r(t)后,通过N点FFT运算将信号转换到频域,再通过不同的检测算法来检测,具体的流程如图1所示。

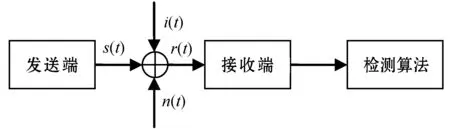
图1 干扰信号接收检测流程框图

假设s(t)为0,即发射端为静默状态,OFDM系统中只存在干扰信号i(t),高斯白噪声信号n(t),则r(t)及其离散化表达式r(n)可表示为:

r(t)=h(t)×i(t)+n(t)

(5)

r(n)=h(n)×i(n)+n(n)

(6)

式中:h(t)为信道增益,干扰信号i(n)和白噪声n(n)相互独立,互不干扰。经过信号采样得到r(n),再经过N点FFT后,转换成频域信号r(k):

(7)

在高斯白噪声环境中检测干扰时,假设两种情况存在:H0表示干扰信号为0,接收信号不受干扰信号的影响,接收信号频域中只有高斯白噪声的频谱n(k);H1表示干扰信号不为0,接收信号受到干扰信号和白噪声信号的影响,接收信号频域中包括干扰信号频谱和白噪声频谱:

H0:r(k)=n(k)

(8)

H1:r(k)=i(k)+n(k)

(9)

2 干扰信号检测算法原理

在频域检测算法中,门限检测法为常见的频域检测算法。频域检测算法不仅可以检测干扰的有无,还可以检测出干扰信号具体的频点分布情况[10]。常见的有基于均值和标准差的检测算法,连续均值去除(CME)算法、前向连续均值去除(FCME)算法。几种常见算法和分段CME算法原理如下:

1) 基于均值和标准差的检测算法:在接收端得到接收信号r(t)后,经N点FFT转换到频域,计算得到频域信号的均值E与标准差σ,然后选择一个门限参数μ乘以标准差,将高于门限值TH的幅值判定为干扰,实现相对简单,表示如下:

TH=E+u·δ

(10)

2) 对于连续均值去除(CME)算法,其实现步骤如下:

① 通过N点FFT转换后得到频谱幅值序列r(k),k∈[1,N],假设无干扰频点幅值集合为x(k),无干扰频点个数为M,干扰频点幅值集合为j(k),干扰频点个数为p,初始时认为频点幅值中没有干扰存在,x(k)等于r(k),M等于N,j(k)为空集,p为0。

③ 对第二步进行多次循环,直到x(k)中的信号不再减少,干扰信号个数p不再增加。最终得出干扰信号集合j(k),完成对信号的干扰检测。

在H0条件下,没有干扰信号的存在,只有高斯白噪声。在接收端,经过FFT后,接收信号近似服从高斯分布,其包络服从瑞利分布[11],均值E(x)和分布函数F(x)为:

(11)

F(x)=1-exp(-x/2σ2)

(12)

由式(11)、式(12)得:

(13)

对于门限值TH等于门限因子T乘以E(x),因此门限因子T等于:

(14)

门限因子T和F(x)的几种取值如表1所示。

表1 F(x)对应的门限因子

在H1条件下,由于干扰信号的存在,将导致接收信号的频谱幅度均值增加,门限值TH变大,将会出现漏检干扰信号的情况。

3) FCME干扰检测算法同样是利用递归和连续迭代的思想[12]。FCME算法在开始阶段只是将经过排序后的最小一部分假定为未受干扰,之后通过迭代运算不断更新门限[13]。通过不断更新的门限值,将大于门限的频点幅值筛除并添加到干扰频点集合,经过多次循环,直到所有的频点幅值都被检测且干扰频点不再增加,最终得出干扰信号集合。

4) 分段CME算法首先将所有的频点幅值进行分组并求每段频点幅值的均值,将均值最小的分段取出作为初始未干扰信号频点集合,来得出初始门限值。后续步骤和CME算法的后续循环更新门限并检测干扰一样,以此进行循环迭代处理,直到不再检测出干扰,最终得出干扰信号集合。

3 改进型CME干扰检测算法

上述几种算法都是频域内算法,基于均值和标准差的检测算法,实现简单,但是漏检率较高。FCME算法的检测性能良好,FCME算法在干扰因子在0.6以上时明显优于CME算法[5],但由于包含排序算法而导致复杂度较高。文献[6]中的分段CME算法,在干扰因子0.6以上时,虽然检测性能强于CME算法,但是要保证分段数足够大,均值最小的分段中不包含干扰信号。对此,本文提出一种改进型的CME算法,使其在分段较低、干扰因子较大的条件下,依然具有不错的检测性能,具体步骤如下:

1) 在接收端得到信号r(t)后,经过N点FFT转换到频域,将N个频点分成Q端,则每段包含有N/Q个整数频点值。求每段频点的均值,并取均值最小的一段频点。

2) 将均值最小的一段频点,与门限值TH0做比较,大于TH0的当做干扰频点,从这一段频点中去除。TH0由基于均值和标准差的干扰检测算法设定,根据初始N个频点值得到整体均值E与标准差σ,TH0=E+u·σ。之后得到新的一段频点,认为这段频点值中没有干扰频点,作为起始未干扰频点集合x0。

3) 对此段频点幅值求均值Ex0,则起始门限值TH=T·Ex0,将除未干扰频点集合x0以外的频点值与门限值作比较,大于TH的判定为干扰频点,添加到干扰频点集合jn中,小于TH的判定为未干扰频点,添加到x0中。

4) 观察jn中干扰频点有无增加,增加则继续步骤3),直到jn中干扰频点不再增加。

5) 改进型CME算法完成,得到最终门限值,并且得出干扰频点集合jn。

相对于FCME算法,提出的改进型CME算法由于没有包含排序算法,算法复杂度较低,比文献[6]中的分段CME算法(CME_B算法)多出了第2步,用基于均值和标准差的检测算法设定的门限值将均值最小分段中的干扰频点筛除掉。在分段数较低或者分段中包含干扰的情况下,可以有效去除干扰,使假设的初始未干扰分段均值较低,接近于无干扰信号均值。

4 仿真分析

为了对上述分析进行验证,本文设置了相应的蒙特卡罗仿真实验。对于不同算法的检测准确性,用检测概率PS来进行表示,同时用虚警率PF和漏检率PM来分别表示干扰检测时将无干扰信号误判为干扰信号的概率和干扰信号被遗漏而未检测出的概率。当检测概率较高且虚警率和漏检率较低时,算法的检测效果越好。仿真条件如下:信道为高斯白噪声信道,信号频域内的子载波间隔为15 kHz,干扰信号为多音干扰,包含的单音干扰个数随着干扰因子变化,分数因子a为0,FFT长度N为2 048,采样频率fs为30.72 MHz。

E-sigma门限法的漏检概率都处在较高的水平[1],因此不予考虑。当干扰因子较高为0.7时,改进型CME算法中的门限参数μ取-0.6;分段CME算法、改进CME算法分段数Q为1 024段,门限因子T都为2.59。由图2可以看出,FCME算法的虚警率最高,表示干扰检测时将无干扰信号误判为干扰信号的概率为最高CME次之,分段CME和改进CME算法的虚警率随着JNR的增大而减小,趋势相近,且虚警率都远小于FCME算法。

图2 四种算法的虚警率比较

干扰因子为0.1,门限参数μ取1,分段数Q为512时。由图3、图4可知,改进型CME算法的检测率随着JNR的增加而趋于1;但检测率和虚警率随着门限因子T的减小而增大。这是由于门限因子T的减小导致门限值降低,能有效检测出幅值较小的干扰频点,使检测率升高,但也造成更多的未干扰频点被误判为干扰频点,使虚警率升高。

图3 不同门限因子T下改进型CME算法的检测率

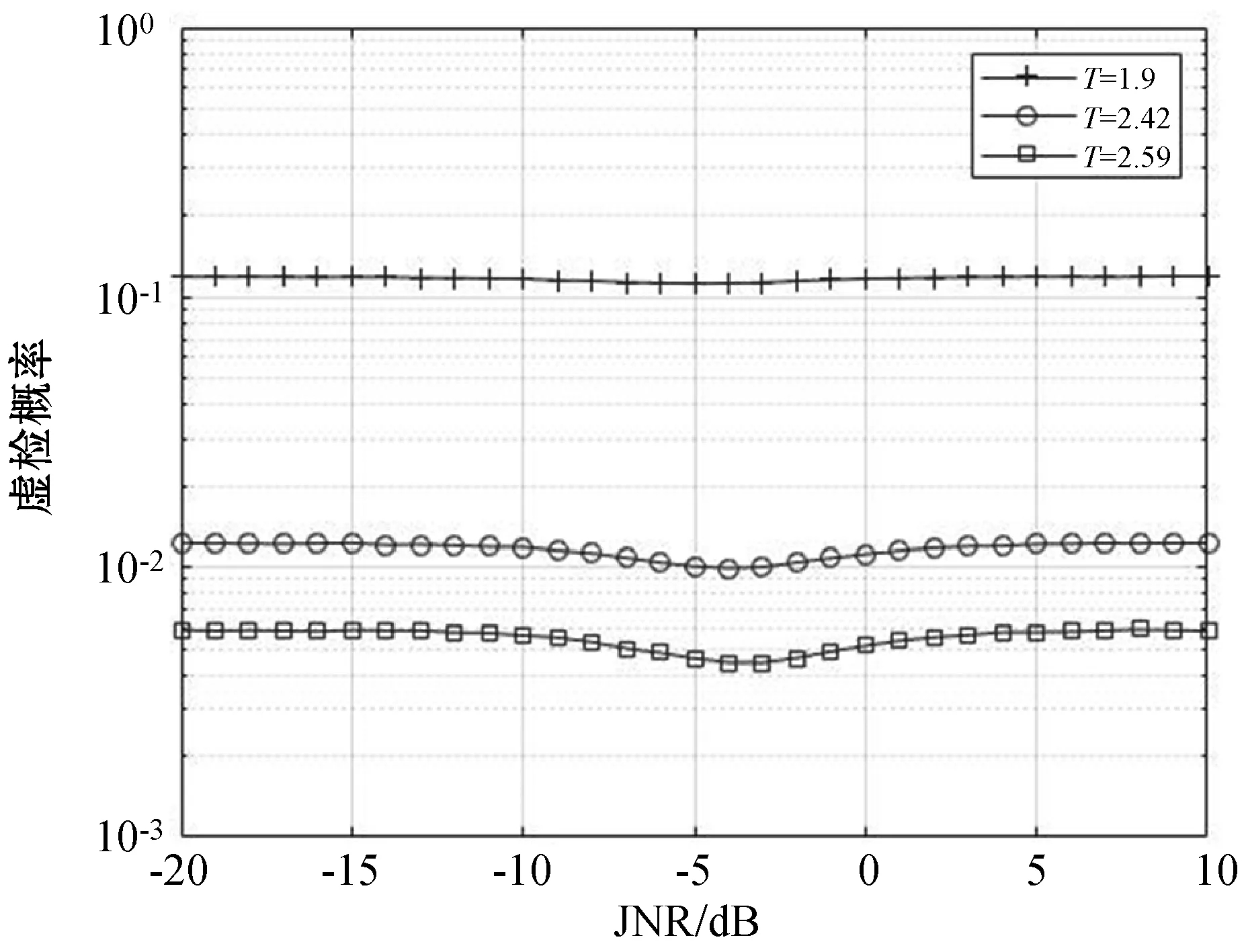
图4 不同门限因子T下改进型CME算法的虚警率

FCME算法在干扰因子为0.6以上时明显优于CME算法[5],则设定干扰因子为0.7;改进型CME算法的门限参数μ取-0.6;门限因子T都为2.59。如图5所示,在干扰因子较高时,分段CME、改进型CME算法与FCME算法的检测率相差不大,都优于CME算法。当把分段CME和改进型CME算法的分段数Q降低为16时,如图6所示,分段CME算法的检测率最差,已不能准确检测干扰,而改进型CME算法依然接近于FCME算法,优于CME算法。这是由于分段数Q较小时,分段CME算法中的最小均值分段包含干扰的概率增大,使生成的初始门限值增大,导致干扰信号漏检,检测率下跌。在改进型CME算法中,将最小均值分段中的干扰信号通过TH0筛除,有效减少了干扰信号的影响。因此在干扰因子较高、分段数Q较低时,改进型CME算法检测率依然优于CME算法和分段CME算法,接近FCME算法,且由于没有包含排序算法,改进算法的复杂度相对于FCME算法较低。

图5 分段数Q为1 024时的四种算法的检测率

图6 分段数Q为16时的四种算法的检测率

5 结 语

本文通过将CME算法和基于均值和标准差的干扰检测算法结合,提出改进型的CME算法,解决了基于均值和标准差算法漏检率较高、CME算法在干扰因子较高时检测率较低的问题。同时在分段数较低和干扰因子较高的情况下,改进型CME算法依然具有良好的检测性能,克服了分段CME算法在分段数较低时检测率较差的问题,又避免了FCME算法中的排序问题。所提改进CME算法仅针对干扰对齐下的多音干扰,未考虑干扰未对齐时的情况,因此在干扰对齐情况下,对基于OFDM系统中的窄带干扰信号是一种有效的、复杂度较低的检测手段。