基于改进混沌映射和WFRFT的射频隐身信号设计
刘光霞,李 琦,韩壮志,魏英珍
(1.河北工业大学 电子信息工程学院, 天津 300401;2.陆军工程大学石家庄校区 电子与光学工程系, 石家庄 050003)
0 引言
在现代电子战争中,雷达至关重要,为了保护雷达避免被敌方探测系统检测到,设计雷达射频隐身信号是一个关键环节[1]。射频隐身信号减弱我方发射信号在传输中的信号特征并且随机性很强,难以被敌方截获,即使被截获,难以识别出信号特性,从而保护我方雷达安全[2]。
近年来,射频隐身信号已成为各国学者研究的热点之一。混沌信号容易设计和控制,并且具有良好的距离分辨率和速度分辨率[3-4],因此混沌映射广泛应用于设计射频隐身信号。许多学者研究经典混沌映射在雷达信号设计的应用,文献[5]设计了一种基于Kent映射的混沌调频雷达信号,具有“图钉型”模糊函数,信号的低截获性能良好。文献[6]提出了一种基于Bernoulli混沌的四相编码OFDM雷达信号设计方法,模糊函数呈图钉状,距离分辨率和速度分辨率具有良好性能。文献[7]提出一种 正交频分复用(orthogonal frequency division multiplexing,OFDM)混沌随机相位编码信号,并对子载波进行混沌调频,得到一种OFDM随机相位随机频率编码雷达信号。但经典混沌映射存在一定局限性,调制信号的射频隐身性能有待提高。
本文中提出了一种基于改进混沌映射和WFRFT的射频隐身信号,改进一维混沌映射对信号调制,对调制信号加权分数阶傅里叶变换,复杂性进一步提高,降低了被截获的风险。
1 加权分数阶傅里叶变换和改进混沌映射设计
1.1 加权分数阶傅里叶变换原理
加权分数阶傅里叶变换(weighted fractional fourier transform,WFRFT)[8-9]是一种新型时频分析技术,最早研究在光学领域,后来在信号处理方面得到应用。该变换具有旋转性,其特性与输入的序列和加权系数有关。输入序列及加权系数设定的随机性,使得输出序列具有不确定性,可以应用在射频隐身信号设计。
加权分数阶傅里叶变换后序列以4为周期,定义为
F(n)=ω0(α)s0(n)+ω1(α)s1(n)+
ω2(α)s2(n)+ω3(α)s3(n)
(1)
式(1)中:s0(n)为长度为n的混沌信号;s1(n)、s2(n)和s3(n)为s0(n)分别进行1、2、3次傅里叶变换。ωm(α)(m=0、1、2、3)是加权系数,表达式为
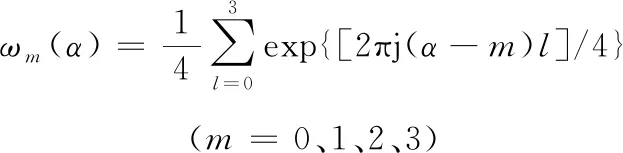
(2)
式(2)中:α为可变参数(即旋转因子);j为虚数。通过改变参数大小,得到不同的加权系数和对应输出函数F(n)。图1是加权系数ω0(α)~ω3(α)随参数α的变换过程。
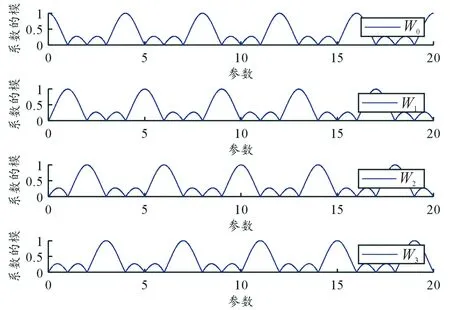
图1 加权系数的模随参数变化过程
1.2 改进一维混沌映射设计
混沌现象是在一个确定系统中出现类似随机、不规则运动,表现出不确定性、不可重复性以及不可预测性。经典一维混沌映射包括Sine混沌映射、Chebyshev混沌映射等。
Sine映射表达式为
xi+1=λ/4sin(πxi)
(3)
式(3)中:xi∈[0,1];xi+1为映射输出序列值;混沌映射参数λ∈[1,4]。从分岔图2(a)可以看出,λ∈(3.6,4]时,输出序列值处于混沌状态,只有λ≈4时,系统处于满映射。同样,Chebyshev映射表达式为

图2 3种混沌映射分岔图
xi+1=cos(λarccos(xi))
(4)
式(4)中:xi∈(0,1);xi+1为映射输出序列值;λ为混沌映射参数,取值范围为[1,4]。分岔图如图2(b)所示,λ∈[1,4]时,混沌系统处于混沌状态,只有λ∈[2,4]时,系统处于满映射。
经典混沌映射存在序列点分布不均匀、映射参数取值范围有限等问题,在一维混沌映射基础上,将2种混沌映射复合变换,解决了经典混沌映射存在问题,增强了序列的不确定性和随机性[10]。结合2种经典一维映射并引入非线性因子,设计了改进一维混沌映射(one-dimensional sine cos-exponential chebyshev,1-SCEC)。定义为
xi+1=cos[π(1-2(cos(λarccos(xi))))2*
(2exp(xi)+exp(-xi))+π(4-λ)/4*
sin(πxi)(2exp(xi)+exp(-xi))]
(5)
式(5)中:xi∈[0,1];xi+1为映射输出序列值;混沌映射参数λ,λ∈[0,4],解决混沌映射参数取值受限的问题。从图2(c)分岔图结果来看,除个别参数取值不均匀,输出序列处于满映射状态。从图2中3种混沌映射对比分岔图可以看出,1-SCEC混沌映射的参数范围更大,参数范围内生成的序列均遍历整个[0,1]状态空间,说明具有良好的均匀分布性[11]。
2 复合调制射频隐身信号设计
2.1 复合调制信号设计
设计脉内调频信号,混沌迭代次数为4 000,初始值设置λ=2,x1=0.152,表达式为
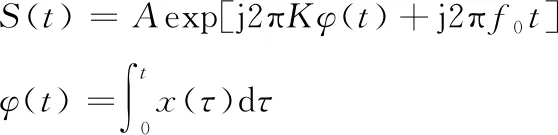
(6)
式(6)中:A为幅度;K为频率调制指数;f0为初始频率;φ(t)为相位函数;xi为混沌映射序列;S(t)为脉内调频信号。将式(6)转换,有:
s(t)=Aexp[j2πKφ(t)]
(7)
对函数s(t)进行离散化,信号的瞬时频率f(t)=[Kφ(t)]′=Kxi,采样频率fs≥2fmax=2Kxmax=K,得到s(n)公式为:
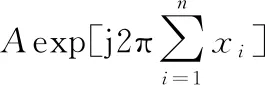
(8)
脉内调频信号仿真结果如图3所示。在此基础上,1-SCEC混沌映射进行脉间调相,迭代次数为50,并进行二值化处理,复合调制信号示意图如图4所示。
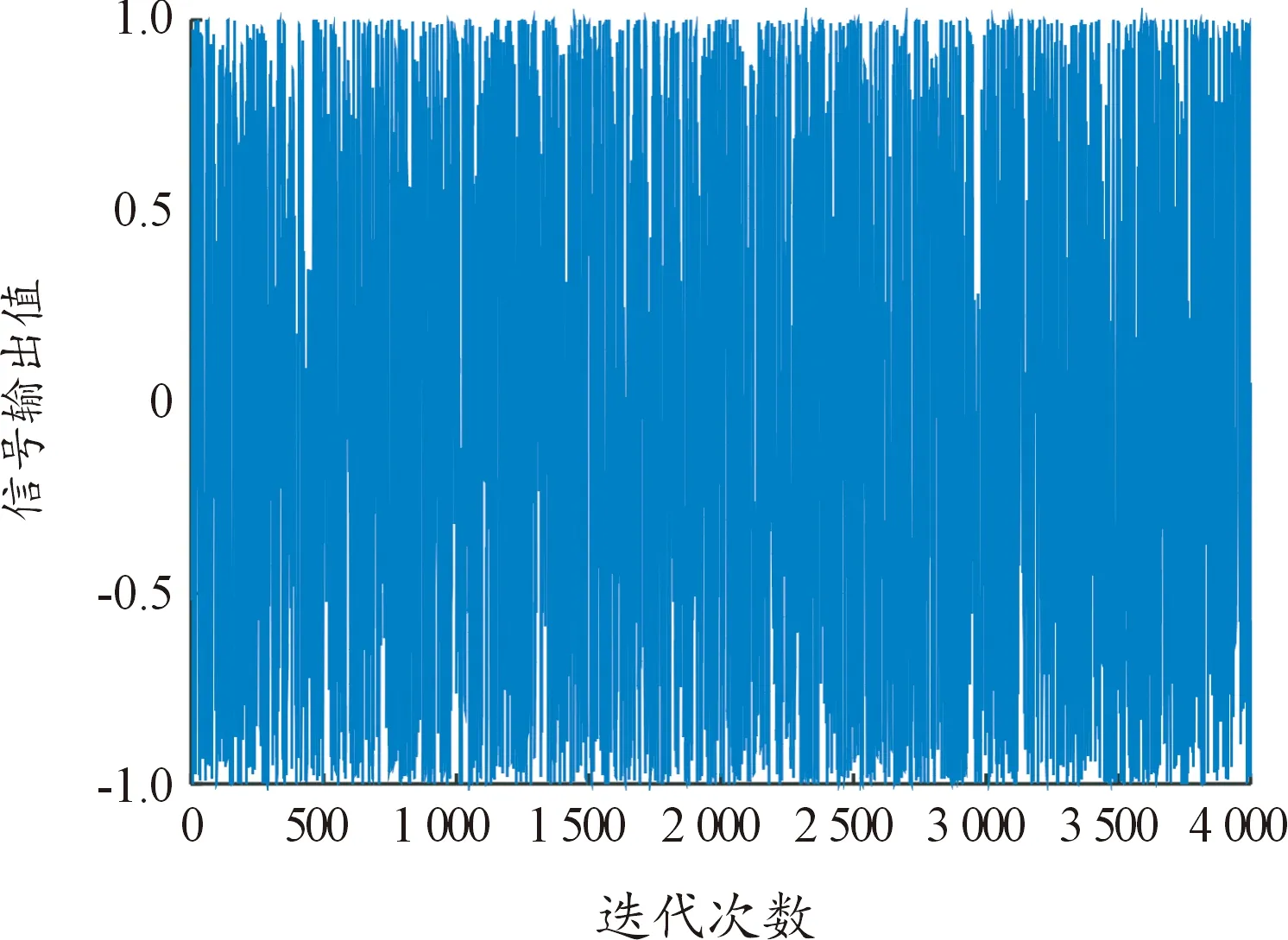
图3 脉内调频信号
图4 复合调制信号示意图
复合调制信号公式为
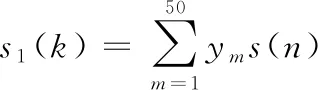
(9)
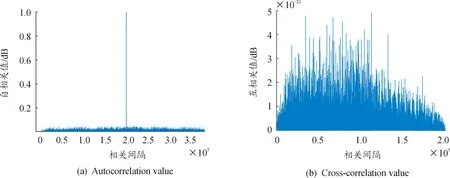
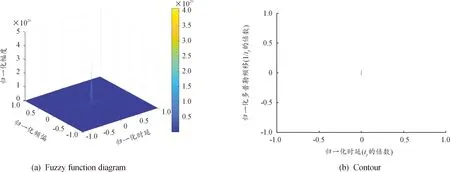
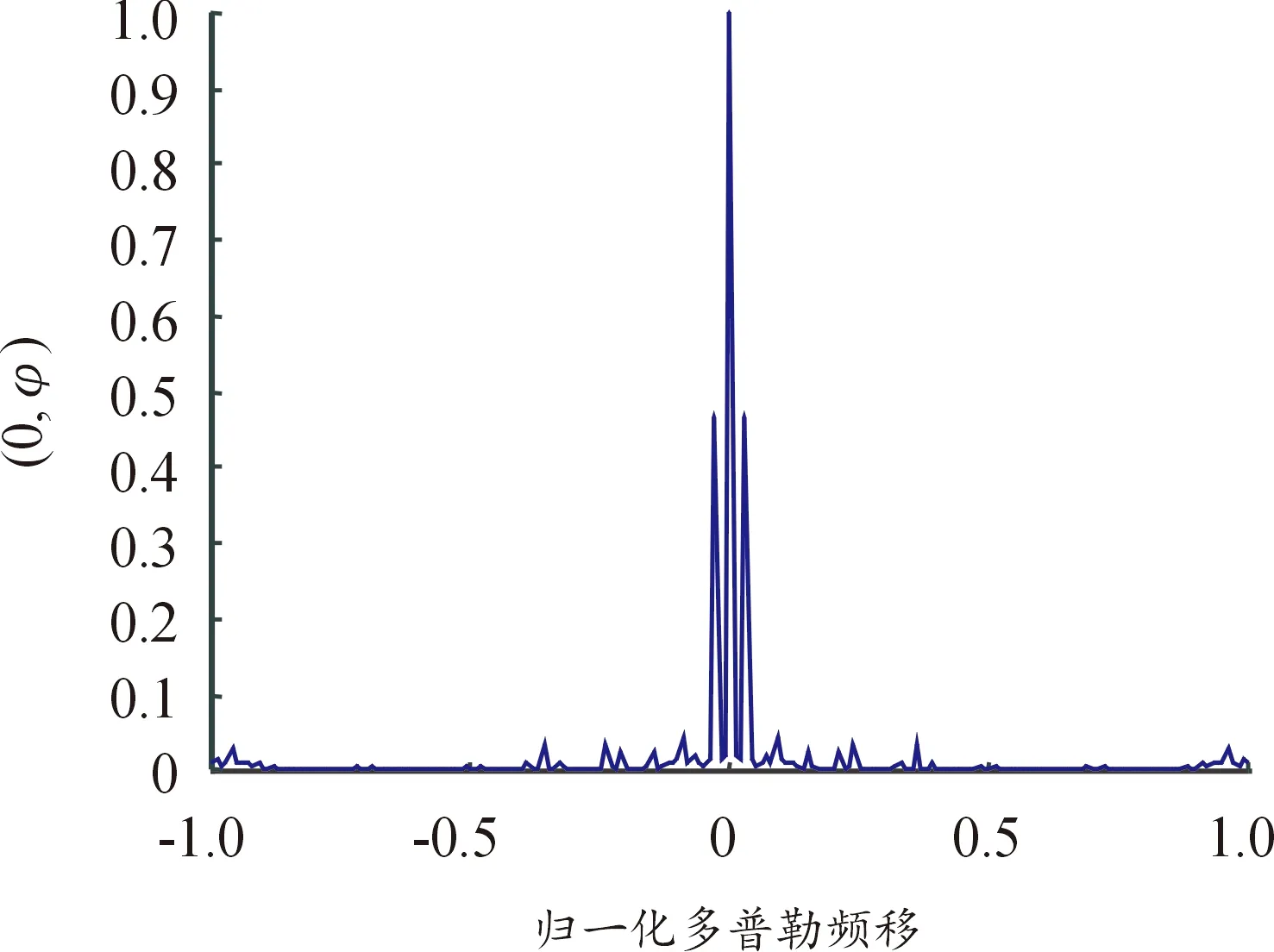
式(9)中:ym为1-SCEC混沌映射二值化结果,最后得到复合调制信号s1(k)(0 图5 复合调制信号 复合调制信号加权分数阶傅里叶变换,α设为2 000,公式为 F(i)=ω0(α)s1(k)+ω1(α)s2(k)+ ω2(α)s3(k)+ω3(α)s4(k) (0 (10) 式(10)中:ω0(α)、ω1(α)、ω2(α)、ω3(α)是加权系数;s2(k)、s3(k)、s4(k)是对s1(k)分别进行1、2、3次傅里叶变换结果;F(i)是对信号加权分数阶傅里叶变换后的结果。其仿真结果如图6所示。 图6 基于WFRFT复合调制混沌信号 3.1.1初值敏感性 初值敏感性是指当给定的初始值发生微小变化时,系统经过混沌映射多次迭代后输出序列值与之前完全不相同。设置1-SCEC混沌映射初始值分别为: (11) 分别迭代200次,得到如图7所示结果。前20次输出值基本吻合,随着后面迭代继续,输出值差距越来越大。只迭代200次,混沌结果就发生明显差距,表明最终将会生成2个完全不同的序列,1-SCEC混沌映射具有初值敏感性。 3.1.2Lyapunov指数 Lyapunov指数是衡量系统动力学特征的一个重要定量指标,表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。Lyapunov指数常用来判定一个系统的混沌性,若Lyapunov指数为正,表示在系统相空间中,无论初始2条轨线间距多小,其差别都会随着时间的演化而成指数增加,最终无法预测,即混沌现象,而且Lyapunov指数越大,混沌现象越明显。反之,则表示初始时刻相邻2点最终会并拢为一点,这对应于稳定的不动点或周期运动点[12]。图8是3种混沌在混沌映射参数变化范围内,Lyapunov指数结果。 图8 基于WFRFT的3种混沌映射Lyapunov指数对比图 从图8可以看出,Sine混沌映射只有在控制参数λ≈4时,Lyapunov指数大于0,在其他参数范围内,都处于不混沌状态。1-SCEC混沌映射Lyapunov指数基本都大于2,Chebyshev混沌映射在λ>1时,Lyapunov指数大于0但小于1.5,说明1-SCEC混沌映射产生的序列复杂性和随机性更强,序列预测难度更大。 3.1.3混沌序列复杂度分析 近似熵(approximate entropy,ApEn)是一种用于量化序列波动的规律性和不可预测性的非线性动力学参数。如果序列的规律性越强,近似熵越小;相反,序列越复杂,缺少规律性,近似熵越大。计算近似熵时,选取较少数据就可以估计出近似熵值,序列长度取1 000左右。表1是基于WFRFT的3种混沌信号取不同参数的近似熵值。 表1 基于WFRFT的3种混沌映射取不同参数的近似熵值 从表1可以看出,1-SCEC混沌映射在取参数值不同时,近似熵值变化不大,均在1.5以上。在参数值一样时,近似熵值大于其他2种混沌映射,说明1-SCEC混沌映射随机性和复杂性很强。 在分析混沌序列复杂性,香农熵和平衡性也常常作为分析的指标。香农熵(shannon entropy,SE)反映了一个系统无序化程度,一个系统越有序,香农熵值越低;反之,香农熵值越高,说明序列越无序、复杂。序列如果处于不平衡状态,会导致信息丢失和泄露,所以评价混沌序列平衡性也是必要的[13]。平衡性公式为 (12) 式(12)中:X为序列中0的数量;Y为序列中1和-1的数量;N为序列长度;E是平衡性值。平衡性大小与序列长度有关,通常将0.01作为衡量平衡性参考值,序列长度设置[0,10 000]。 从图9(a)看出,1-SCEC混沌映射参数λ∈[0,4]时,香农熵值基本在7.6左右。而Chebyshev混沌映射只有在λ∈[1.5,4]时,稳定在7.6左右,其他参数内从0开始递增。Sine混沌映射香农熵值只有λ∈(3.5,4]在7.5附近,其他参数内都低于3。对比这3种混沌映射说明,在混沌映射参数范围内,1-SCEC混沌映射序列一直处于复杂状态。 图9 基于WFRFT的3种混沌映射香农熵值和平衡性值对比 图9(b)比较3种混沌映射平衡性,随着序列增长,3种混沌映射都趋于量级0.01平稳状态。但Chebyshev混沌映射会出现平衡性值大于0.01的情况,1-SCEC混沌映射平衡性值一直处于0.01以下,说明1-SCEC混沌映射平衡性良好。 3.2.1相关性能 在衡量射频隐身信号性能时,自相关性能和互相关性能是必不可少的衡量指标。通常用峰值旁瓣比和积分旁瓣比比较信号的低截获特性。当信号自相关函数具有较低旁瓣,即峰值旁瓣比值和积分旁瓣比值越小,则信号测距精度越好,旁瓣携带能量越少,则被截获后获得的有效信息越少[14]。 峰值旁瓣比和积分旁瓣比公式为 (13) 式(13)中,R(i)(i=0,±1,…,±N)是混沌信号的相关函数。下面比较3种混沌信号自相关、互相关性能。 3种混沌信号自相关性能值如表2所示,从表2可知,基于WFRFT的1-SCEC混沌信号PSL为-81.274 7 dB,ISL为-72.084 9 dB,和表2中其他2种信号比较,结果值都要小,说明基于WFRFT的1-SCEC混沌信号自相关性良好,低截获和抗识别特性突出。表3是互相关的峰值旁瓣比和积分旁瓣比,对调制后的信号进行加权分数阶傅里叶变换,其峰值旁瓣比和积分旁瓣比都有明显改进,生成的信号互相关性能更低。 表2 3种混沌信号自相关性能值 表3 3种混沌信号互相关性能值 图10是基于WFRFT的1-SCEC混沌信号自相关值和互相关值,由图10可以看出,自相关函数尖锐,主瓣很窄,则测距精度越好,旁瓣比较低,则信号能量主要集中在主瓣上,互相关值位于0值附近,数值非常小,说明2个序列的相似度很低。综上,基于WFRFT的1-SCEC混沌信号作为射频隐身信号,抗识别性能更强。 图10 1-SCEC混沌信号的自相关值和互相关值 3.2.2功率谱 功率大小是衡量射频隐身信号性能的一个重要指标,当信号的最大功率刚好达到需要传输最远距离的最小功率时,则可以降低被截获的风险,从而实现射频隐身[15]。 图11是信号功率谱波动范围,混沌调频信号和混沌调频调相信号的波动较大,基于WFRFT的1-SCEC混沌信号的波动范围最小,功率谱更平坦,频谱利用率越高。从表4看出,基于WFRFT的1-SCEC混沌信号最大功率比混沌调频信号和混沌调频调相信号低-9 dB左右。从平均功率来看,3种信号基本相等,混沌调频调相信号比其他2种信号低-3 dB左右。 表4 1-SCEC混沌信号功率变化过程 3.2.3模糊函数 模糊函数可以有效分析信号距离分辨率和速度分辨率,观察模糊函数在原点处图型,分析信号能量分布[16-17]。 混沌信号F(t)的模糊函数为 (14) 式(14)中:χ(τd,φd)是F(t)的模糊函数;τd是时延;φd是多普勒频移。 距离模糊函数和速度模糊函数[18]公式分别为: (15) (16) 基于WFRFT的复合调制信号模糊函数仿真结果如图12—图14所示。 图12 基于WFRFT的复合调制信号模糊函数及等高图 由图12可以看出,该模糊函数图近似“图钉型”,能量集中在τd=0和φd=0处,旁瓣很低且平坦,表明该信号有很强的低截获特性。同样从等高图直观地看出,该信号能量集中在原点处。 由图13和图14可以看出,主瓣宽度很窄,该信号具有良好的距离分辨率和速度分辨率。以上分析说明,该信号性能达到射频隐身信号的特性。 图13 距离模糊图 图14 速度模糊图 本文中提出了一种基于改进混沌映射和WFRFT的射频隐身信号,通过仿真实验,得到以下结论: 1) 通过分析表明改进一维混沌映射的随机性和复杂性优于经典一维混沌映射。 2) 引入加权分数阶傅里叶变换,通过对加权系数控制,信号更加难以被识别,提高信号的抗截获性能。 3) 对比Sine混沌映射和Chebyshev混沌映射产生的混沌信号,从相关性能、功率以及模糊函数方面对信号进行分析。实验结果表明,1-SCEC混沌信号具有良好的抗识别性能,适合作射频隐身信号。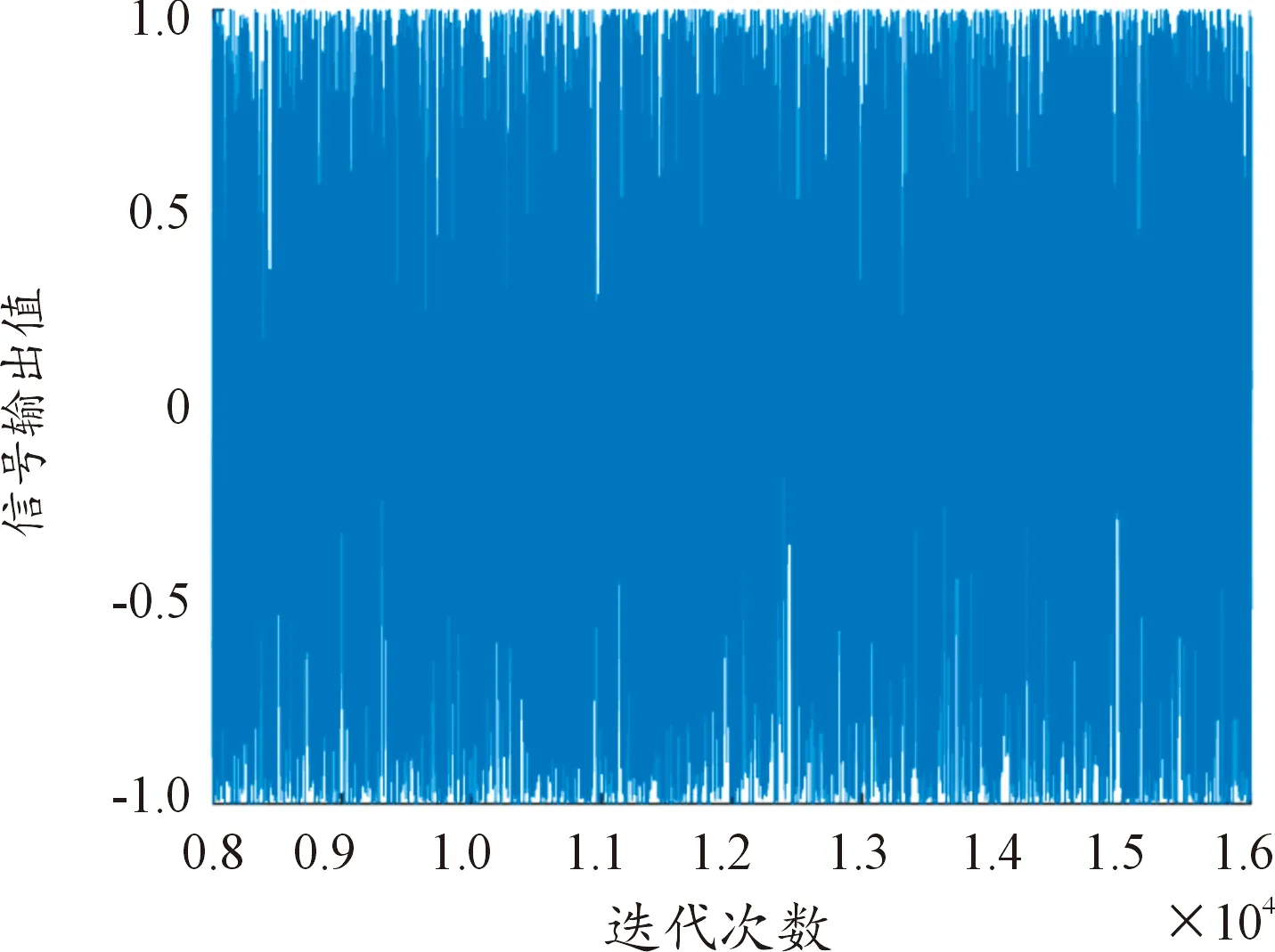
2.2 基于WFRFT的复合调制信号设计
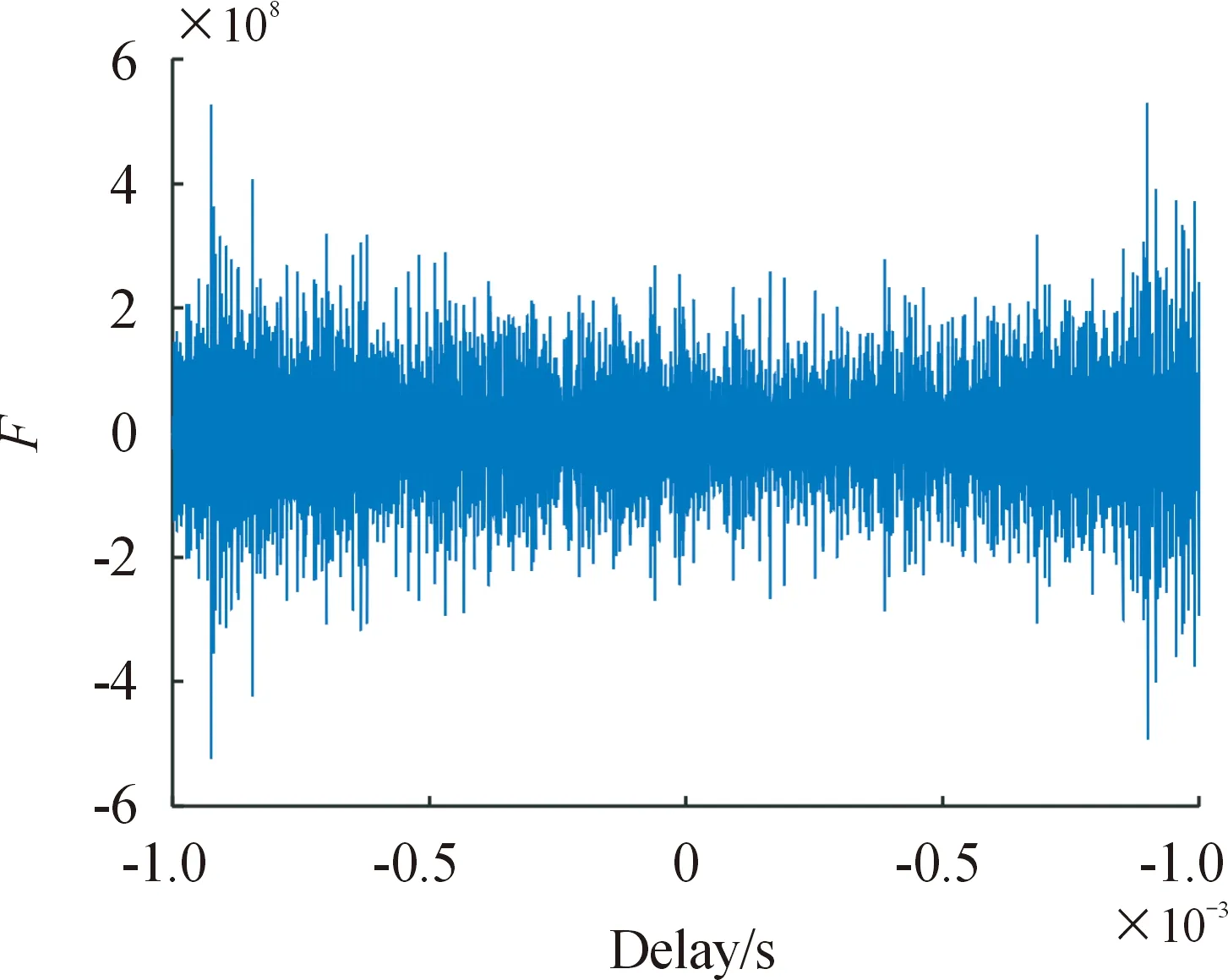
3 仿真性能分析
3.1 改进一维混沌映射性能分析


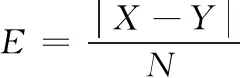

3.2 基于WFRFT的复合调制信号性能分析
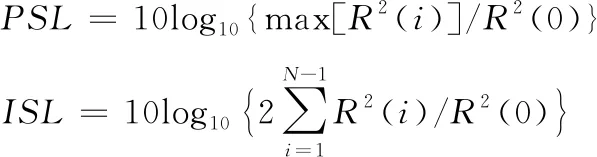


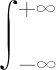

4 结论

