Impact point prediction guidance of ballistic missile in high maneuver penetration condition

Yong Xin ,Le-ling Ren ,* ,Y-jie Xu ,Sho-peng Li ,b ,Wei Wu ,D-qio Zhng

a Xi'an Research Institute of High Technology,Xi'an,710025,China

b Department of Automation,Tsinghua University,Beijing,100084,China

Keywords:Ballistic missile High maneuver penetration Impact point prediction Supervised learning Online guidance Activation function

ABSTRACT An impact point prediction (IPP) guidance based on supervised learning is proposed to address the problem of precise guidance for the ballistic missile in high maneuver penetration condition.An accurate ballistic trajectory model is applied to generate training samples,and ablation experiments are conducted to determine the mapping relationship between the flight state and the impact point.At the same time,the impact point coordinates are decoupled to improve the prediction accuracy,and the sigmoid activation function is improved to ameliorate the prediction efficiency.Therefore,an IPP neural network model,which solves the contradiction between the accuracy and the speed of the IPP,is established.In view of the performance deviation of the divert control system,the mapping relationship between the guidance parameters and the impact deviation is analysed based on the variational principle.In addition,a fast iterative model of guidance parameters is designed for reference to the Newton iteration method,which solves the nonlinear strong coupling problem of the guidance parameter solution.Monte Carlo simulation results show that the prediction accuracy of the impact point is high,with a 3 σ prediction error of 4.5 m,and the guidance method is robust,with a 3 σ error of 7.5 m.On the STM32F407 singlechip microcomputer,a single IPP takes about 2.374 ms,and a single guidance solution takes about 9.936 ms,which has a good real-time performance and a certain engineering application value.

1.Introduction

The ballistic missile (BM) maneuver penetration system is mainly composed of the inertial navigation system (INS),onboard computer,detection and perception system,divert control system(DCS) and attitude control system.Its characteristic is that it still has the ability of navigation,guidance and ballistic correction after the end of the boost phase.In response to anti-missile interception systems[1],the mid-course maneuver penetration[2-4]of BMs is considered to be one of the most effective ways.However,the uncertainty of deployment positions,interception strategies and interception timings of anti-missile systems makes maneuver directions,maneuver timings and the number of maneuvers uncertain.Therefore,planning before launching on the ground to determine the nominal trajectory is impossible.

Generally,current BM guidance methods are mainly based on perturbation guidance [5]and closed-loop guidance [6].Perturbation guidance is based on the theory of small deviations to control the actual flight near the nominal trajectory,thereby achieving precise control of the impact point.Closed-loop guidance uses the control functional to calculate the required velocity in real time to control the BM to meet the terminal constraints(minimum impact deviation) according to the target information and the current flight state of the BM.To adapt to the calculation ability on the BM,the solution is simplified by hitting the virtual target point with an elliptical trajectory.However,the virtual target point is still calculated based on the nominal trajectory.The implementation of existing BM guidance methods all rely on the nominal trajectory,whereas the nominal trajectory of the high maneuver penetration(HMP) BM (HMPBM) cannot be calculated.Therefore,an urgent need exists to study an adaptive online guidance method for the HMPBM.

With the continuous development of guidance theory,a large number of studies have been conducted on the application of the orbit entry of launch vehicles with guidance methods,such as optimal guidance [7,8]and iterative guidance mode [9,10],which are based on the optimal control theory.This kind of guidance method does not rely on the nominal trajectory in terms of the orbit entry problem,and the optimal guidance parameters are calculated according to the current flight state and the target orbit parameters[11].Given that there exists a certain similarity between the precise orbit entry of launch vehicles and the precise strike of BMs,this type of algorithm can be applied to BMs.However,these algorithms rely on assumptions,such as vacuum environment and constant gravity field [11],resulting in insufficient robustness [12].Therefore,by relying on the nominal trajectory,the problem of simplifying the calculation on the BM may exist.At the same time,this type of algorithm has a large amount of calculation and unstable multidimensional iterative convergence [11],which restrict its engineering application.

According to the related references,the impact point prediction(IPP) guidance [13,14]and predictor-corrector guidance [15-19],which refer to the model predictive control [20-22]idea,do not rely on the nominal trajectory.These methods predict the terminal state based on the current state of the system and then feedback to correct the guidance parameters,which have strong adaptability and good robustness.This type of guidance method plays an important role in the guidance of hypersonic vehicles and highspin rockets,and many improvements have been made for different simulation assumptions.

The two core problems that need to be solved by this type of guidance algorithm are as follows:one is to study a high-accuracy IPP algorithm adapted to the calculation ability of the BM according to the current flight state;and the other is to rapidly solve the guidance parameters under multiple constraint conditions based on the IPP.This type of guidance method has the problem of poor real-time calculation [16].The main reason is that the traditional IPP algorithm cannot consider the requirements of calculation efficiency and prediction accuracy [23,24].For example,the computation cost was reduced by simplifying the model in Refs.[16,17];however,the accuracy of the IPP was not high.In Refs.[14,19],the IPPs with higher accuracy were obtained through the numerical integration method (NIM),but the real-time performance was difficult to meet the requirement.The difficulty of IPP is that the reentry-phase trajectory is affected by the non-spherical perturbation of the earth and aerodynamic drag,which make the solution of the impact point more nonlinear and difficult to predict accurately.Generally,the high-accuracy IPP is obtained by the NIM[14,19,25,26];however,this method requires plenty of computing resources [27],of which the real-time performance is difficult to meet the requirement.

In recent years,machine learning methods have been widely used in the field of flight vehicle design[28-33]due to their strong nonlinear fitting ability.To achieve the high-accuracy and fast IPP,the rapid prediction methods of flight trajectory are studied based on machine learning methods.Ref.[23]used the deep neural network(DNN)to realize the trajectory prediction.Ref.[25]studied the IPP of hypersonic vehicles based on DNN.Ref.[34]used the machine learning method based on the Gaussian process to study the trajectory prediction of the BM in the boost phase.The machine learning methods have a certain potential in trajectory prediction.However,the general problems of the above methods are that the neural network (NN) model has a large structure,and model adaptability is insufficient.Moreover,some differences exist between the above methods and the application scenarios in this study.

As far as the guidance parameter solution is concerned,the impact point of unguided trajectory will deviate greatly from the target point after the HMP,which brings about the nonlinearity and enhanced coupling of the guidance parameter solution.However,the classical method of using the secant method[35]to iteratively solve the guidance parameters faces the problem of nonconvergence in the solution of multidimensional variables.On the basis of the small perturbation method,the first-order linear mapping relationship between the guidance parameters and the impact deviation was established in Ref.[14],which is more accurate than the classical fixed mapping relationship method.However,there still exists a certain model error under strong nonlinear conditions.The difference between the present work and Ref.[14]is that the IPP is based on the NN,and guidance parameters are calculated online by the Newton iteration method.Moreover,the advantages of the method proposed in this study are that the number of IPPs required is small,the convergence speed is fast and the real-time performance is good.

Generally,the HMPBM usually uses the DCS to correct the impact deviation.Therefore,the use of rated parameters for correction control will cause a large actual impact deviation when there exists a large deviation between the actual parameters of the DCS and its normal rated parameters.Refs.[25,36]studied the fault-tolerant guidance problem when the aerodynamic coefficients are changed due to the failure of the hypersonic vehicle actuator,whereas few studies have been conducted on the guidance problem under the condition of the large deviation of the DCS parameters.

On the basis of the above analysis,an IPP guidance based onsupervised learning (SL) is proposed in this study,aiming at the online precision guidance problem of BMs after the HMP.The main contributions of this study are as follows.

(1) On the basis of SL,a guidance framework suitable for HMPBMs is designed,with good real-time performance and strong robustness.

(2) On the basis of the improved sigmoid activation function and the decoupling prediction of the impact point,an NN model for the IPP is designed,which has the characteristics of small network structure,high prediction accuracy and fast calculation speed.

(3) For the same type of BMs,the NN does not need to be trained before launching,which is beneficial to shorten the preparation time of the data calculation of BMs.

(4) To meet the requirement of guidance fault tolerance,a fast iterative algorithm for guidance parameters with strong robustness to DCS thrust force deviation,thrust direction deviation and propellant second consumption deviation is designed based on the apparent acceleration of the INS output.

The outline of this paper is organized as follows.Section 2 describes the precise guidance problem of HMPBMs,where the accurate ballistic trajectory model and guidance constraints are given.In Section 3,a framework for the IPP guidance is designed,which mainly includes a module of an IPP based on SL and a robust solution module for guidance parameters.In Section 4,an SL-based IPP model is established,including sample generation,network structure design,activation function improvement and model training.On the basis of Section 4,Section 5 establishes a guidance parameter solution algorithm based on the apparent acceleration of INS outputs.In Section 6,a series of simulations are conducted on the models proposed in Sections 4 and 5.Finally,conclusions are presented in Section 7.

2.Problem formulation

The maneuver penetration is to change the original inertial flight trajectory by applying thrust to BMs through the DCS,thereby increasing the difficulty of trajectory prediction of anti-missile systems and improving the penetration probability.The HMP indicates a large deviation from the nominal trajectory,and the guidance method based on the nominal trajectory will not meet the accuracy requirement.

The working process of HMPBMs can be described as follows:

(1) On the basis of a certain penetration strategy,the HMP is realized by adjusting the attitude and applying the thrust through the attitude control system and the DCS,respectively.

(2) After the penetration succeeds,the BM attitude is adjusted by the attitude control system,and thrust is applied by the DCS again to realize the correction of the impact deviation,which is based on a certain guidance algorithm(the research content of this study).

2.1.Fundamental assumption

Assuming that the DCS is installed at the tail of the HMPBM warhead,the thrust direction is forward along the axial direction of the HMPBM warhead,the thrust is constant and the engine working time is controllable.Attitude adjustment can be accomplished quickly by the attitude control system.

The process of HMPBMs to correct impact deviation is as follows.Firstly,the HMPBM attitude is adjusted to the designated value through the attitude control system.Then,the DCS is switched on to apply axial thrust.Finally,the DCS is switched off after the terminal impact point constraint is satisfied.

2.2.Accurate solution model of the impact point

In this study,the passive phase is defined as the entire process from the current flight state to the end of the flight after the HMP,which includes two parts: the flight phase in the vacuum and the flight phase in the atmosphere.Note that the HMPBM is uncontrolled in the atmosphere at zero angle of attack.

In view of the rotational ellipsoid and re-entry aerodynamic drag,the dynamic equation under the earth-centred earth-fixed(ECEF) coordinate system(CS;ECEF-CS) is established as follows:

The gravitational acceleration considering the J2perturbation of the earth can be described as

2.3.Guidance constraints

According to the correction process of the impact deviation of HMPBMs in subsection 2.1,and at the same time,considering the performance of the DCS,attitude control system and onboard computer,the constraints can be obtained as follows.

(1) The attitude adjustment angular velocity constraints are expressed as

(2) The thrust forceFDCSconstraint is expressed as

(3) The working timetDCSof the DCS constraint is expressed as

whereTmaxis the maximum working time of the DCS.

(4) The re-entry terminal constraint is expressed as

where Xfandare the actual impact point vector and target point vector,respectively;and εLHis the maximum threshold of the impact deviation.

(5) The solution time constraint of the guidance algorithm is expressed as

wheretgis the time required to solve the guidance algorithm after the DCS is switched on;ΔTis the guidance period;and α is a constant,representing the maximum proportion of the solution time of the guidance algorithm in the whole guidance period.

3.Framework for the HMPBM IPP guidance

To take advantage of the IPP guidance algorithm in robustness and improve its real-time performance,an IPP guidance framework of HMPBMs based on SL is designed in this study to meet the demand for precision guidance after the HMP.The framework comprises an IPP NN model(IPPNNM)and a robust guidance parameter calculation model.

The guidance framework designed in this study is shown in Fig.1.In the offline learning stage,after the overall parameters of BMs are determined,the training set is generated based on the accurate solution model of the impact point in Subsection 2.2,and the IPPNNM is obtained through training.In the online guidance stage,the following process is looped in each guidance period until the impact point accuracy requirement is met.Firstly,the impact point is predicted according to the current flight state of the HMPBM,and the longitudinal and lateral deviations of the predicted impact point relative to the target point are calculated.Then,the guidance parameters are calculated based on the small disturbance method.Finally,after the flight state is updated according to the guidance parameters,the new impact point is predicted,and the new longitudinal and lateral deviations are calculated to determine whether the accuracy requirement of the impact point is met.A closed-loop control process is formed.

Fig.1.IPP guidance framework of HMPBMs based on SL.

4.SL-based IPP modeling

This section presents the design of the IPPNNM and introduces the offline learning method.The pseudocode of the IPPNNM in the online guidance stage is then summarized.

4.1.IPPNNM

Given that the NN has a strong nonlinear fitting ability,it can be used to fit the nonlinear mapping relationship between the current flight state of the HMPBM and the impact point.The following factors need to be considered in the design of the NN:

(1) The range of the training samples should cover all possible flight states of the HMPBM to improve the generalization ability of the model.

(2) To adapt to the calculation ability of the HMPBM,the network structure size is as small as possible under the constraint of prediction accuracy.

A strong coupling relationship exists between the three components of the impact point in the ECEF-CS,which increases the difficulty of network learning.To reduce the coupling degree between the impact point coordinate components and improve the network convergence speed,the mapping relationship between the flight state of the HMPBM and the impact point is established in this study.

The current flight state of the HMPBM in the ECEF-CS is assumed to be(Xs0,Vs0),and the impact point is.Taking the projectionmof Xs0on the ground as the origin,mxnynzn-CS is established.mxnynzn-CS is defined as follows.mis the origin of the coordinates.Themynaxis passes through the center of the earth and points to the sky.Themxnaxis points north and is perpendicular to themynaxis,and themznaxis forms a right handed orthogonal system with the other two axes.According to Eq.(11),the HMPBM current flight state (Xn0,Vn0)with

where Xnand Vnare the position vector and velocity vector in themxnynzn-CS,respectively;Xsand Vsare the position vector and velocity vector in the ECEF-CS,respectively;reis the earth radius of pointm;andis the transformation matrix from the ECEF-CS tomxnynzn-CS,which can be expressed as

To predict the impact point according to the current flight state of the HMPBM,the mapping relationship between them is established,as shown as follows:

wheref1(·) is the mapping function.

Given that the origin ofmxnynzn-CS is the projection of the current position of the HMPBM on the ground,Xn0＝[0,Hm,0]Tcan be obtained,withHmbeing the height.Given that the earth is ellipsoid and has rotation,the latitude of the HMPBM has a certain influence on the impact point,and the improved prediction model is expressed as

wheref2(·) is the improved mapping function.

Given that the NN prediction model can be regarded as a complex fitting function,the fitting effect of the NN can be improved by increasing the physical quantities that affect the impact point.The prediction model is then further improved as follows:

wheref3(·) is the further improved mapping function,andg(Xn0,Vn0) can usually be defined as the mapping function between(Xn0,Vn0)and the local flight-path angle Θ,velocity azimuth σ,velocityV,and other physical quantities.A detailed simulation analysis ofg(Xn0,Vn0) is conducted by ablation experiments in Section 6.1.

Generally,the NN structure of the IPP is in the form of the multilayer perceptron (MLP),which can predict the impact point well after training.However,problems exist with a large network structure and difficult learning.After the impact point is expressed in-CS,the coupling between the different components of the impact point is reduced,which reduces the difficulty of NN learning and network structure.Given that different components of the impact point have great differences,to further reduce the scale of the network structure,three similar NN models are designed to predict the three coordinates of the impact point,as shown in Eq.(17).For the convenience of description,the three NN models are denoted as networksx,yandz.

wheref4x(·),f4y(·) andf4z(·) are the mapping function between the current flight state of the HMPBM and the different components of the impact point;andgx(·),gy(·)andgz(·)are theg(·)of the three NN models.

The structures of networksx,yandzare shown in Fig.2.The structures are all in the form of an MLP with two hidden layers,and the difference is the input and output of the NN model and the number of hidden layer nodes.In Fig.2,denotes the nodes of the input,hidden and output layers,anddenotes the activation function.

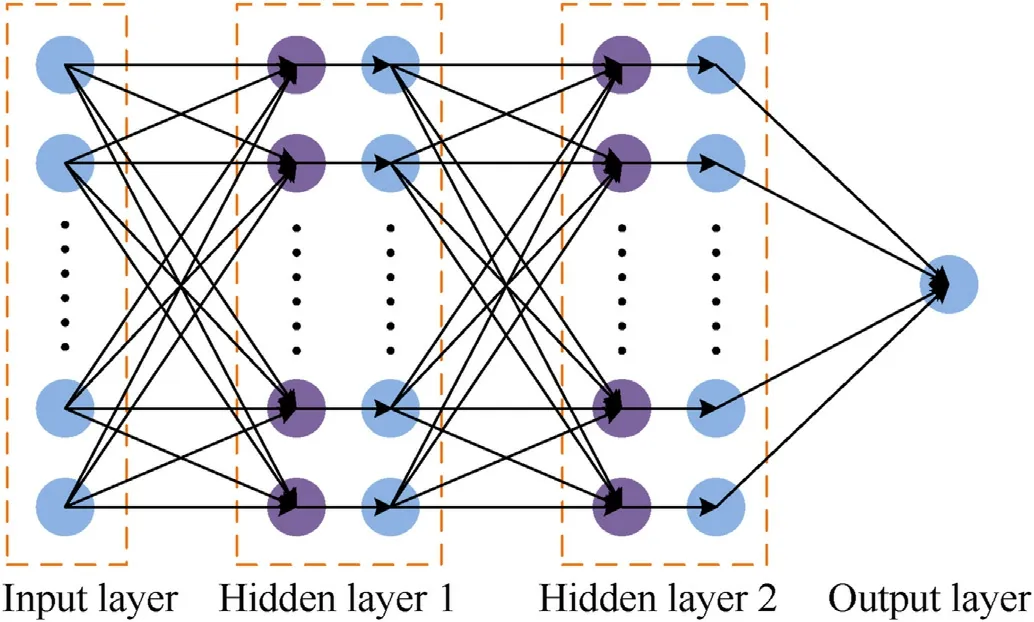
Fig.2.Network structure diagram of the IPPNNM.

4.2.Design of the improved activation function

Generally,NN models usually use the sigmoid [37],tanh [37]and rectified linear unit (ReLU) [38]as activation functions.Particularly,the ReLU shows good performance in the DNN.However,the sigmoid and tanh have stronger nonlinear fitting ability in shallow networks.Given that the sigmoid and tanh have a similar fitting ability,the sigmoid is studied and analysed in this study.The expression of the sigmoid is shown in Eq.(18).However,its computation is relatively large,which reduces the real-time advantage of the prediction model.

wherexis the input of the sigmoid.

From Eq.(18),the existence of the exponential function exp(·)is the main reason for a large amount of calculation of the sigmoid.To improve the calculation speed of the NN prediction model,this study improves the sigmoid by reducing the calculation amount,and a new activation function,called the simplified sigmoid (SSigmoid),is proposed,which can be expressed as follows:

On the basis of the sigmoid,the S-Sigmoid is obtained by simplifying exp(·)as a second-order Taylor expansion.As shown in Fig.3,the S-Sigmoid is derivable,continuous and monotonically increasing in the domain;and the range is (0,1).The S-Sigmoid only abandons the high-order term of exp(·);thus,it still retains most of the characteristics of the sigmoid.Therefore,the NN based on the S-Sigmoid has the fitting ability close to the NN based on the sigmoid,whereas the calculation amount is considerably smaller than that of the latter.

Fig.3.Sigmoid,S-Sigmoid and corresponding derivative function curve.

4.3.Sample generation modeling

To ensure that the IPPNNM has better prediction accuracy,the training set must cover all possible flight states of the HMPBM.Hence,the flight state space set S is defined as

where Hs,φs,Vs,σsand Θsare the sets discretized of the flight height,latitude,velocity,velocity azimuth,and local flight-path angle,with discrete intervals of δH,δφ,δV,δσand δΘ,respectively.

The larger the state space range in S is,the larger the NN structure will be needed to complete the high-precision prediction.To reduce the size of the NN structure and improve the calculation speed,S is decomposed according to the height in this study.Hence,Si⊂S(i＝1,2,3…) is derived as

To better test the generalization ability of the model,the following test and validation set sample generation method is adopted.Taking the upper and lower bounds determined by Hs,i,φsVs,σsand Θsas the range,each variable is subject to a uniform distribution;andNinitial states are randomly generated.By using the same method as generating the training samples,the coordinates of the impact point in-CS are then obtained.Ntest or validation samples are also obtained.

4.4.NN training method

To overcome the problem of the low training efficiency caused by the inconsistent scale of each variable in the input vector,the min-max normalization method is used to normalize the data,as shown as follows:

wherepdenotes a variable,pmindenotes the minimum of the variable,pmaxdenotes the maximum of the variable and～pis the normalized result.

In this study,the NN loss function uses the mean square error(MSE) function [30],and the optimizer uses Levenberg-Marquardt algorithm [39,40].The Levenberg-Marquardt algorithm is an improvement of the Newton method,which can avoid nonconvergence when the Jacobian matrix is singular or illconditioned.It is the fastest convergence algorithm in the medium-scale NN training,which is 10-100 times faster than the traditional gradient descent algorithms [40].

4.5.Online IPP algorithm procedure

Although the training process of the IPPNNM takes a long time,the online run is extremely fast after the training is completed,and the procedure is shown as Algorithm 1.

Pseudocode.

Algorithm 1.IPPNNM

5.Online guidance algorithm modeling

In Section 4,the core problem of the IPP guidance engineering application is solved;that is,the IPP should consider the high precision and rapidity.This condition allows multiple IPP in the guidance period,which provides the possibility for the design of online guidance algorithms.In this section,the mapping relationship between guidance parameters and the impact deviation is analysed based on the variational principle,and the rapid solution model of the guidance parameters under the condition of DCS performance perturbation is then studied based on the IPPNNM.

5.1.Analysis of mapping relationship between guidance parameters and impact correction

Generally,the guidance algorithm of the HMPBM can be established in the launching CS (LCS),and the longitudinal range and lateral distance of the impact point can be described as a functional of the position and velocity [14],as shown as follows:

where vx(t),vy(t),vz(t),x(t),y(t)andz(t)are the functions the ofx-,y-andz-axis velocity and position attmoment in the LCS.

Given that after the thrust force is applied to the HMPBM,the position and velocity will be changed during a guidance period,resulting in a new longitudinal rangeL*and lateral distanceH*,as shown as follows:

where Δvx,Δvy,Δvz,Δx,Δyand Δzare the velocity and position variation caused by the thrust force.

Generally,the guidance period ΔT＝20 ms is taken,which is extremely short.Therefore,the position variation is relatively small in a guidance period.Moreover,the sensitivities of the position variation toL*andH*are relatively small;thus,the influence of the position variation onL*andH*can be ignored.At the same time,in practical engineering applications,considering that it is difficult to adjust the three-dimensional attitude of the HMPBM in the midflight,the attitude is usually adjusted only in one plane.Hence,is selected as the apparent-velocity-to-begained to correct the longitudinal and lateral deviations.The longitudinal range correction ΔLCand the lateral distance correction ΔHCobtained by Eq.(29) and Eq.(30) can be expressed as

Expanding Eq.(31) by the variational principle yields

where ∂L/∂vx,∂L/∂vz,∂H/∂vxand ∂H/∂vzare the sensitivity coefficients;and H.O.T denotes higher-order terms.

5.2.Guidance algorithm design

After determining the mapping relationship between the guidance parameters and the impact point correction,it is necessary to further establish the guidance parameter calculation model through the impact deviation,which is expressed as follows.

5.2.1.Calculation modeling of the apparent-velocity-to-be-gained

Given that the accuracy of the BM impact point is usually described by the longitudinal and lateral deviations,the impact deviation ΔR can be obtained by combining Eq.(32),as shown as follows:

where ΔLpand ΔHpare the longitudinal and lateral deviations of the predicted impact point relative to the target point,respectively.The schematic diagram of the impact deviation is shown as Fig.4.

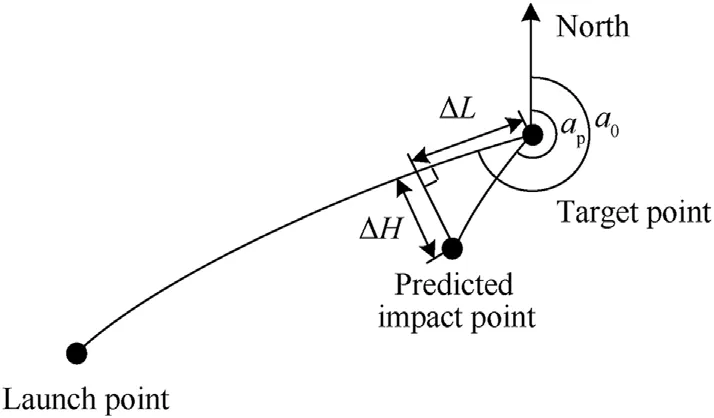
Fig.4.Schematic diagram of the impact deviation.

Fig.5.Error bar of the test set MSE of the f4x(·)NN model versus the training epochs.

Considering that the distance between the predicted impact point and the target point of the guided trajectory is very small,to reduce the amount of calculation,ΔLpand ΔHpcan be obtained by the principle of spherical geometry,as shown as follows:

with

wherermis the earth radius at the target point;βpis the angular distance between the predicted impact point and the target point;a0is the azimuth angle between the launch point and the target point;apis the azimuth angle between the predicted impact point and the target point;and φmand λmare the geocentric latitude and geocentric longitude of the target point,respectively.

Note that the nonlinearity between the impact deviation and the apparent-velocity-to-be-gained is enhanced after the HMP.That is,ignoring the H.O.T of Eq.(32) will lead to large errors.Hence,the Newton iteration method is used to design the iterative calculation method with the apparent-velocity-to-be-gained based on the small disturbance model.The expected impact point of the HMPBM under ideal conditions is the target point.That is,the impact deviation ΔR is

Substituting Eq.(32) into Eq.(37) yields

The iterative formula constructed by Eq.(38) is

where superscriptsiandi+1 denote variable value in iterationsiandi+1,respectively.

From Eq.(8),the termination condition of the iteration is

The sensitivity coefficients are usually calculated by the nominal trajectory before launching.However,the nominal trajectory of the HMPBM cannot be determined.At the same time,given that the IPPNNM established in Section 4 has the characteristics of high precision and fast calculation,the online calculation method of HMPBM sensitivity coefficients is adopted.That is,small perturbations on vxand vzare added to calculate the longitudinal and lateral deviations,respectively,and the sensitivity coefficients can then be obtained by Eq.(41).

where δvxand δvzare the small perturbations of velocity in thexandz-axis,respectively;F(·) is a function to calculate the longitudinal and lateral deviations according to the apparent-velocityto-be-gained at timetk.

The calculation process ofF(·) is as follows.Firstly,the flight state oftkis updated according to the apparent-velocity-to-begained,and the impact point is then predicted by the Algorithm 1.Finally,the longitudinal and lateral deviations are calculated by Eq.(34).

In view of the short time interval between the two adjacent guidance periods,there exists little difference in ΔWgbetween the adjacent guidance periods.Therefore,after solving ΔWgthrough Eq.(39)in the first guidance period,the corresponding variables of the previous guidance cycle in other guidance periods are used as the initial iteration values,which will reduce the time consumption of the algorithm convergence.At the same time,Eq.(39) needs to solve an inverse matrix.Hence,given that the velocity in thex-axis mainly affectsL,and that in thez-axis mainly affectsH,(i.e.∂L/∂vx≫∂L/∂vz,∂H/∂vz≫∂H/∂vx),to further improve the calculation speed,the decoupling and simplification of Eq.(39) can be derived as

On the basis of the above analysis,the procedure of the algorithm for solving ΔWgis shown in Algorithm 2.

Procedure.

Algorithm 2.Apparent-velocity-to-be-gained solving algorithm

5.2.2.Controlled variable calculation modeling

From the process of HMPBMs to correct the impact deviation given in Section 2.1,the controlled variable vector P is

where φCis the pitch controlled variable,ψCis the yaw controlled variable,and ΔtCis the working time of the DCS.

After obtaining ΔWgaccording to Algorithm 2,φCand ψCcan be expressed as

Combining the control performance constraints given by Eq.(5)yields

where φ and ψ are the pitch and yaw angles in the current flight state,respectively.

When ｜φ-φC｜→0 and ｜ψC-ψ｜→0,that is,the attitude of the HMPBM is controlled as the required attitude,the DCS is switched on,and the working time ΔtCis

5.3.Robust guidance algorithm design

Generally,the performance parameters of the same type of different DCSs are similar but not exactly the same.The rated values are the average value of the corresponding parameters;thus,there exists a certain deviation between the actual and rated parameters.The deviations of the main parameters are the thrust force deviation,thrust axis deviation(including pitch and yaw axis deviations)and propellant second consumption deviation.

When the DCS parameters have large deviations,the guidance algorithm established by the rated DCS parameters in Section 5.2 faces the problem of insufficient robustness.Therefore,the guidance algorithm considering the DCS parameter deviations must be established.From Eq.(45)and Eq.(47),the purpose of designing φC,ψCand Δtcis to ensure that the apparent velocity increment of the HMPBM reaches ΔWgconstraints at the same time after the DCS works Δtc.Given that the high short-term accuracy of the INS,the apparent velocity increment in a guidance period can be accurately obtained.Therefore,in this section,the guidance algorithm established in Section 5.2 is improved based on the apparent velocity increment information output by the INS.

As the navigation equipment of the HMPBM,the INS can be sensitive to the apparent acceleration,which is the acceleration generated by the DCS under the vacuum condition.The INS output is the apparent velocity increment Δ＝［Δ,Δ,Δ］Tof the inertial LCS (navigation CS of the HMPBM) within 1 navigation period ΔTg.Given that the guidance algorithm in this study is established in the LCS,it must be converted to the LCS to obtain ΔW ＝［ΔWx,ΔWy,ΔWz]Tby Eq.(49).

with

where ωx,ωyand ωzare the projections of the angular velocity vector of the earth rotation in the LCS.

The apparent acceleration a in the LCS can be obtained as

The thrust direction deviation is caused by the DCS axis deviation,which results in the pitch controlled variable deviation ΔφCand the yaw controlled variable deviation ΔψC,as shown as follows:

By combining Eq.(45) and Eq.(52),the improved pitch controlled variable φCand yaw controlled variable ψCare depicted as

From Eq.(47),the thrust force deviation and propellant second consumption deviation will cause the calculation error of ΔtC.Hence,after correcting the pitch and yaw controlled variable deviations,the calculation formula of the improved ΔtCis expressed as

On the basis of the above analysis and in view of the deviation of DCS parameters,the robust guidance algorithm is designed,as shown in Algorithm 3.

Procedure.

Algorithm 3.Robust guidance algorithm

6.Analysis and discussion

This study assumes that the mass of the HMPBM is 500 kg[42],the DCS can provide 5 g overload,the DCS maximum working timeTmaxis 3 s,and the maximum pitch and yaw rates are 10°/s.Taking subset S1of S as an example,a large number of simulation experiments at different ranges are used to determine the set of flight states S1considering the influence of the HMP,as shown in Table 1.At the same time,Table 1 presents the discrete interval of the initial state.

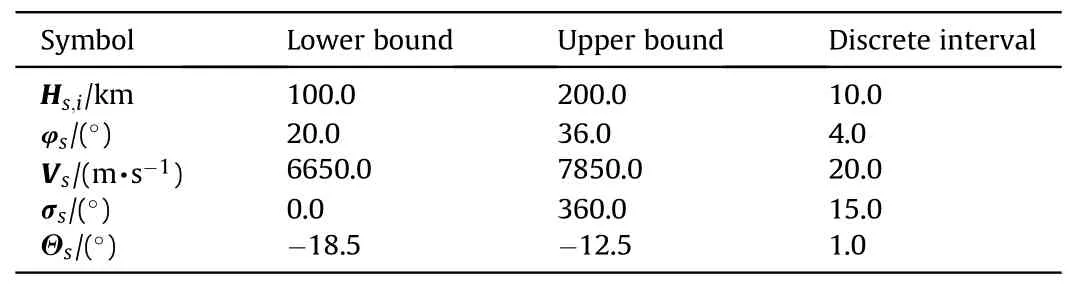
Table 1Flight state range.

6.1.SL-based IPP simulation analysis

6.1.1.IPPNNM input analysis

The mapping relationship between the flight state and the impact point established by Eq.(17)requires further determination ofgx(Xn0,Vn0),gy(Xn0,Vn0) andgz(Xn0,Vn0).In this study,the combination of Θ,σ andVis determined,and the optimal input combination is studied by ablation experiments.Table 2 shows the simulation setting.

Table 2Ablation experiment setting.

The larger the number of samples is,the longer the training time will be.Therefore,to shorten the duration of ablation experiments,the flight state range is set as a subset of the set given in Table 1.To study the effects of the different inputs on the NN performance,the number of hidden layer nodes of the NN is set to 6 and 7,and the hidden layer activation function is sigmoid.The training set,validation set and test set(10000 samples)generation methods of the simulation are shown in Section 4.3;and the training is performed 100 times for each input situation.Given the influence of the random initialization of network model parameters,the convergence performance of each training is different.To better reflect the generalization ability of the NN,the MSE curve of test set versus the training epochs (100-30000 epochs) is plotted as shown in Figs.5-7,and the y-axis is presented in the form of logarithmic coordinates.The MSE of the test set is used as the NN performance index,and the test performance statistics over 100 independent trainings are shown in Table 3.

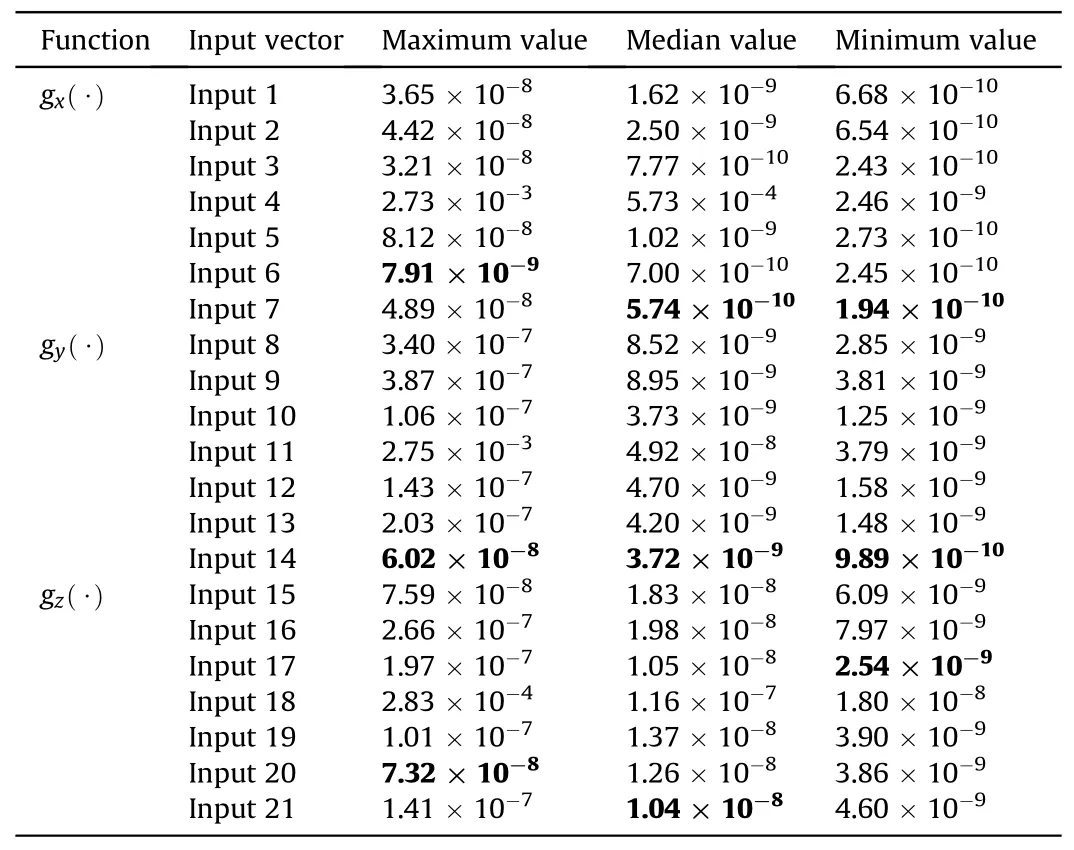
Table 3Test set MSE statistics over 100 independent trainings.

As shown in Figs.5-7,the NN performance of different input vectors has a large gap,and the network performance of Inputs 4,11 and 18 is the worst,corresponding to the situation where σ is the input.The NN performance of Inputs 7,14,and 17 is better,corresponding to the case where (Θ,V) or (Θ,σ,V) is applied as the input.For thef4x(·) NN model,the minimum and median of the error bar curve corresponding to Input 7 are the smallest,indicating that the NN performance of this input vector is better than that of the other inputs.However,the maximum value is greater than the maximum value of Input 6,indicating that it is more sensitive to NN initial parameters.As shown in Fig.6 and Table 3,the minimum,median and maximum values of the error bar curve corresponding to Input 14 of thef4y(·)NN model are the smallest,indicating that the training process has stable convergence,minimum test error and good generalization ability.For thef4z(·)NN model,except for the NN with Input 18,the NN performance gap of different input vectors is relatively small (Fig.7 and Table 3).The minimum,median and maximum values of the error bar curve corresponding to Inputs 17,21 and 20 are the smallest.At the same time,the median of the error bar curve corresponding to Input 17 and 21 is approximately equal.The median and minimum of the error bar curve can better reflect the performance of the NN;thus,

Fig.6.Error bar of the test set MSE of the f4y(·)NN model versus the training epochs.

Fig.7.Error bar of the test set MSE of the f4z(·)NN model versus the training epochs.

Fig.8.Error bar of the test set MSE of different activation functions of the f4x(·) NN model versus the training epochs.

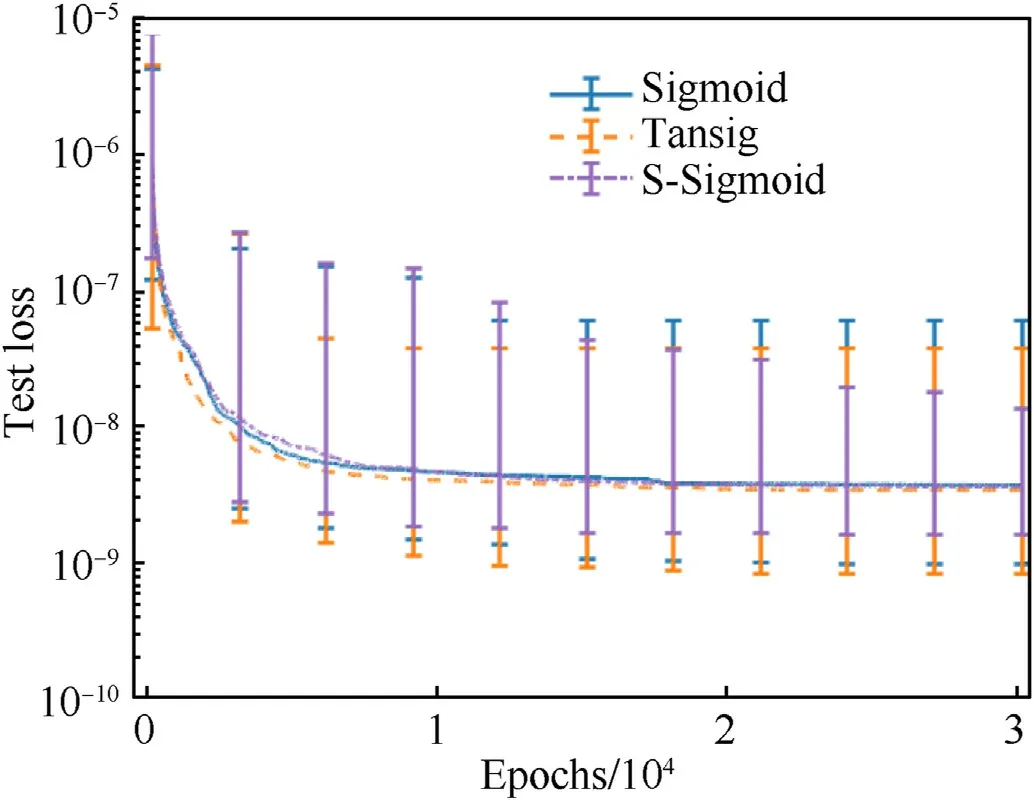
Fig.9.Error bar of the test set MSE of different activation functions of the f4y(·) NN model versus the training epochs.

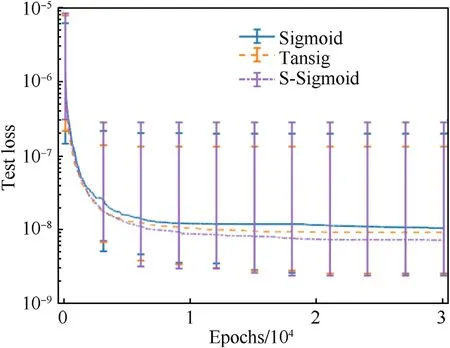
Fig.10.Error bar of the test set MSE of different activation functions of the f4z(·) NN model versus the training epochs.

6.1.2.Performance analysis of different activation functions

To test the effectiveness of the improved activation function SSigmoid,whether the S-Sigmoid maintains the prediction accuracy of the original NN model should be verified.On the basis of the network model input determined by Eq.(55),the hidden layer activation functions are set as sigmoid,tanh and S-Sigmoid.For each network trained 100 times,the MSE curve of the test set versus the training epochs(100-30000 epochs)is plotted as shown in Figs.8-10.The test performance statistics over 100 independent trainings are shown in Table 4.

Table 4Test set MSE statistics of different activation function NN models over 100 independent trainings.

As shown in Figs.8-10 and Table 4,in thef4z(·)NN model,the performance of S-Sigmoid is better than that of sigmoid and tanh.In thef4x(·)andf4y(·)NN models,the maximum value of the error bar curve corresponding to S-Sigmoid is smaller,and the median and minimum values of the error bar curve corresponding to SSigmoid are similar to those of sigmoid and tanh.Therefore,the performance of S-Sigmoid is similar to that of sigmoid and tanh,and using S-Sigmoid as the activation function can achieve highprecision IPPs.

6.1.3.IPPNNM-based IPP accuracy analysis

On the basis of the input vector and activation function of the IPPNNM determined in Sections 6.1.1 and 6.1.2,the number of hidden layer nodes must be further determined to ensure prediction accuracy.With the increase in the number of hidden layer nodes,the prediction error will decrease.However,the calculation amount will gradually increase.To ensure that the prediction accuracy is high and the amount of calculation is minimum,a large number of simulation experiments are conducted based on the flight state range of the HMPBM given by Table 1 to determine the number of the IPPNNM nodes as shown in Table 5.According to the test set generation method in Section 4.2,10000 test samples are randomly generated,and the test error is counted,as shown in Fig.11.

Table 5Number of hidden layer nodes.

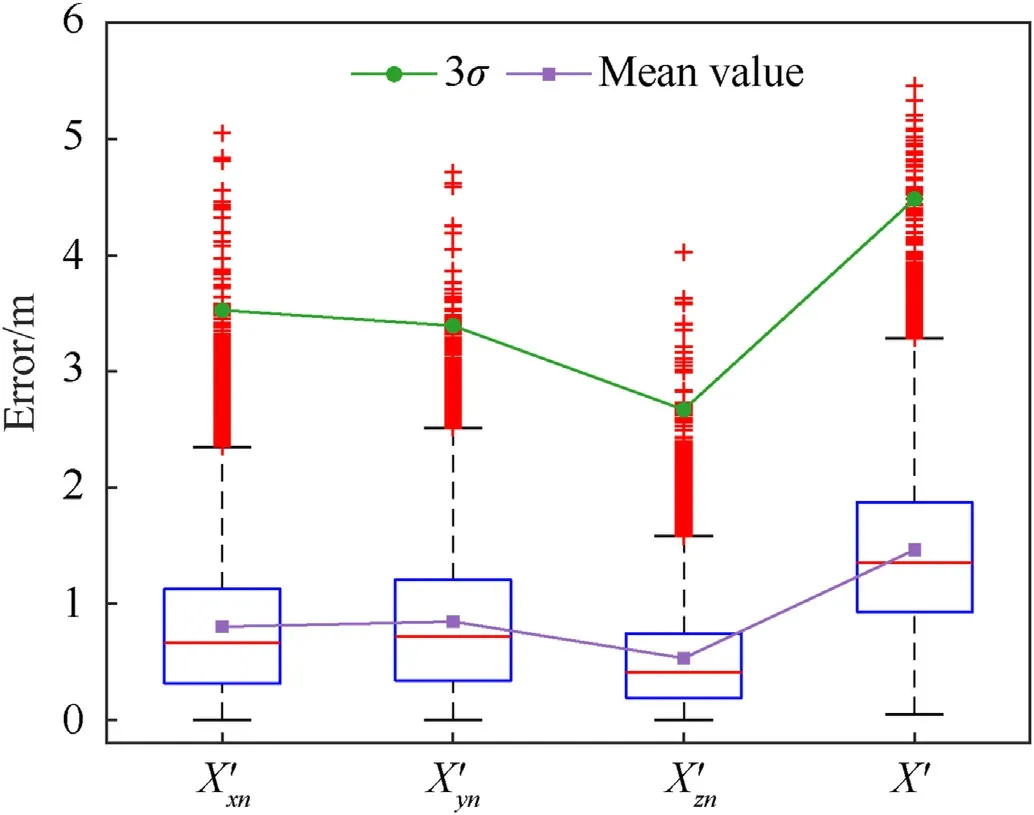
Fig.11.Impact point prediction deviations.

Fig.11 shows the prediction errors of the three components,andof the impact pointusing thef4x(·),f4y(·)andf4z(·)NN models,respectively.The maximum value of the prediction error does not exceed 5.1 m,and the 3σ value and the average value do not exceed 3.6 m and 0.9 m,respectively,indicating that the three prediction models have strong generalization ability and high prediction accuracy.At the same time,Fig.11 shows the prediction error of,that is,the distance between the predicted and actual impact points.Its maximum value is 5.5 m,and the 3σ value and average value are 4.5 m and 1.5 m,respectively,indicating that the overall prediction accuracy is high.Meanwhile,as shown in Table 5,the number of nodes of thef4z(·) model is relatively small at only about half of the number of nodes of thef4x(·)model.It shows that expressing the impact point in-CS reduces reducing the learning difficulty of the network model.For the same type of BMs,since the overall parameters are the same,the corresponding training sets are the same.Combined with the flight state range generation method in Table 1,the trained model can fulfill the IPP requirements of the same type of BMs under different range conditions after HMP.Hence,the accurate predicted impact point required by the online guidance model can be given by the IPPNNM.

6.1.4.Computational complexity analysis of the proposed IPPNNM

According to the analysis in Sections 6.1.2 and 6.1.3,the prediction network using S-Sigmoid can maintain high prediction accuracy.To further verify the effectiveness of the S-Sigmoid,whether S-Sigmoid significantly reduces the amount of network computing should be verified.

In this study,the STM32F407 single-chip microcomputer is used as the experimental platform to test the CPU run time of the IPPNNM using S-Sigmoid,sigmoid and tanh activation functions,and the prediction model based on NIM.The statistical run time is shown in Fig.12.The NIM adopts the Adams-Moulton method,which has high integration accuracy and small computation [41], and the integration step is 0.2 s.When the single-chip microcomputer operation data types are double and float,Fig.12 shows the overall run time of the single prediction of different methods,the run time of the NN and the run time of the NN input and output transitions.The time consumption corresponding to the float data type is more than 3 times shorter than that corresponding to the double data type.At the same time,on the basis of the 10000 test samples in Section 6.1.3,the calculation accuracy of NN models with two data types is counted,and the corresponding calculation results are obtained.The maximum deviation of the results of the two data types is 2.7 m.Hence,in the case of small demand for the accuracy of the IPP,float data type can be applied for IPP calculation.

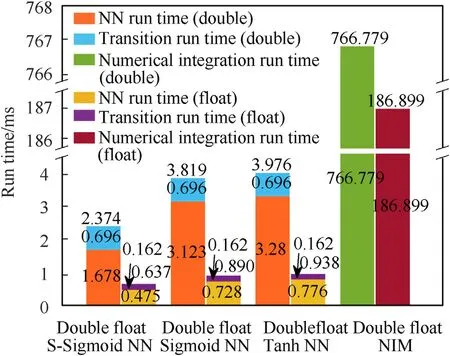
Fig.12.Run time of different models.

As shown in Fig.12,the prediction model based on the NN takes considerably less time than the prediction model based on the NIM,and the difference between the two is two orders of magnitude.The time consumption of the NN using S-Sigmoid is less than that using sigmoid and tanh.The overall run time corresponding to the double data type is reduced by 1.445 ms and 1.602 ms,which are reduced by 46.3% and 48.8%,respectively.In addition,the overall run time corresponding to the float data type is reduced by 0.253 ms and 0.301 ms,which are reduced by 34.8% and 38.8%,respectively.Therefore,the improved NN prediction model based on the S-Sigmoid can effectively reduce the prediction time and improve the real-time performance.

6.2.Online guidance algorithm analysis

According to the simulation analysis in Section 6.1,the NN prediction model based on the S-Sigmoid activation function has high-accuracy and good real-time performance,which can meet the requirement of the guidance algorithm.On this basis,the accuracy and robustness of the online guidance algorithm are further simulated and analysed.

To analyse the performance of the guidance algorithm,the flight state of the nominal trajectory of the HMPBM is taken as the initial condition of the simulation,and the state deviation experiment is conducted on this basis.Assuming that at timet(zero time in this paper),the nominal trajectory height of the HMPBM is 179 km;the position vector and velocity vector in the LCS are[6532056.91,-6794525.28,288882.06]Tm and[-2469.74,-6521.98,331.39]Tm/s,respectively;the velocity is 6981.81 m/s;the local flight-path angle is-16.41°,and the velocity azimuth angle is 96.85°.To perform the state deviation experiment,the position deviation ‖ΔR0‖～U[1,5]km and the velocity deviation‖ΔV0‖～U[20,100]m/s of the initial flight state are assumed.The parameter deviations of the DCS are shown in Table 6.

Table 6Parameter deviations of the DCS.

6.2.1.Single guidance performance analysis

Fig.13 and Fig.14 show the variation curves of the pitch angle,yaw angle and ΔtCversus time in the guidance process,respectively.The attitude of the HMPBM is adjusted in 0-6.44 s,and the DCS is switched off at this stage.After the attitude is adjusted to the required attitude,the DCS is switched on at 6.44-9.033 s to correct the impact deviation.As shown in Fig.13 and Fig.14,the pitch and yaw angles of the HMPBM and ΔtCare adjusted after the DCS is switched on.The main reason is that the HMPBM attitude and ΔtCare updated by Algorithm 3 according to the apparent velocity increment of the INS output.

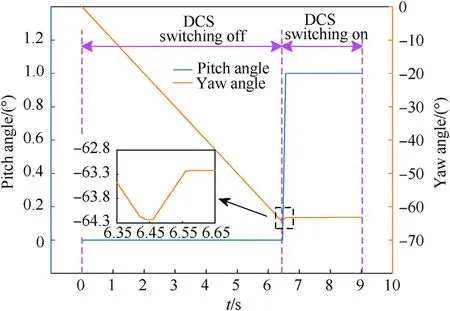
Fig.13.Variation curves of the pitch and yaw angles versus time.

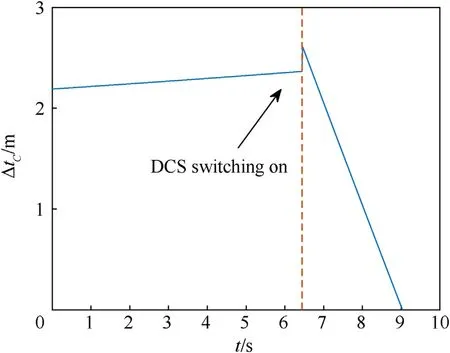
Fig.14.Variation curve of ΔtC versus time.

Fig.15 shows the three-dimensional trajectories for the nominal trajectory,the unguided trajectory after adding the initial state deviation,and the guided trajectory corrected by the method in this study.The curves of velocity and local flight-path angle versus time are shown in Fig.16 and Fig.17,respectively.The flight state of the unguided trajectory is quite different from that of the nominal and guided trajectories.Hence,if the unguided trajectory is not corrected,then the impact deviation will be extremely large.As shown in Table 7,the longitudinal and lateral deviations of the unguided trajectory impact point are -13215.02 m and -9332.08 m,respectively;whereas the longitudinal and lateral deviations of the guided trajectory impact point are -4.26 m and -2.45 m,respectively.Hence,Algorithm 3 greatly improves the impact point accuracy.

Table 7Impact deviation of the unguided and guided trajectories.

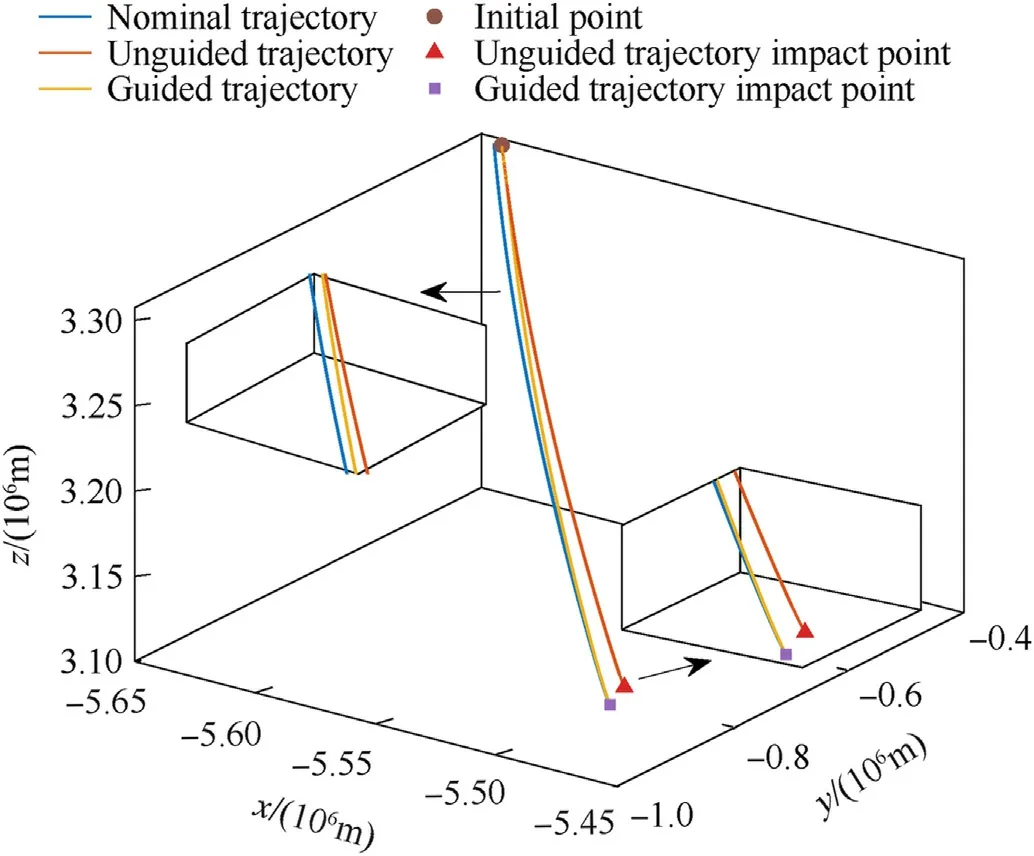
Fig.15.Three-dimensional trajectory.

Fig.16.Curves of the velocity versus time.

Fig.17.Curves of the local flight-path angle versus time.

To further test the effectiveness of the guidance algorithm in this study,the perturbations of the thrust force,propellant second consumption and attitude in the working process of the DCS are added.The perturbation range is shown in Table 8,where δP,,and δare the perturbations of the thrust force,pitch angle,yaw angle and propellant second consumption,respectively.On the basis of the above discussion,the simulation results obtained by adding the perturbations are shown in Fig.18 and Fig.19.The DCS attitude and ΔtCare constantly changing to correct the influence of perturbations.The longitudinal and lateral deviations of the guided trajectory are -5.18 m and -2.58 m,respectively,indicating that Algorithm 3 has strong robustness when the perturbations are within a certain range.

Table 8Perturbations of the DCS.

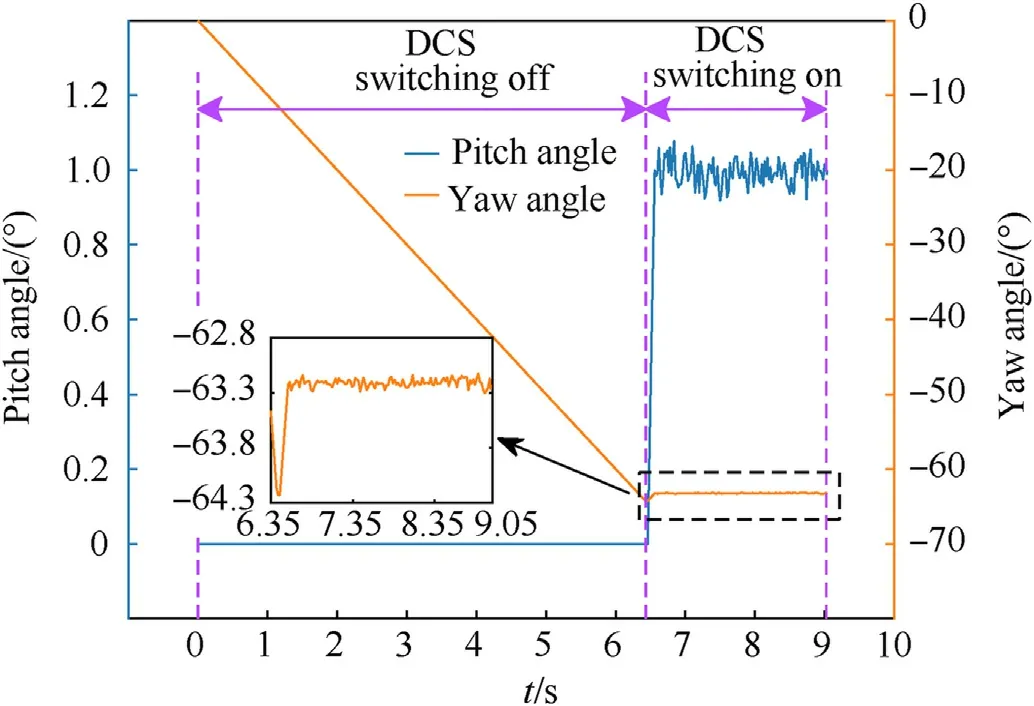
Fig.18.Variation curves of the pitch and yaw angles versus time with the added perturbations.

Fig.19.Variation curve of ΔtC versus time with the added perturbations.

Fig.20.Three-dimensional guided trajectory histories (100 cases).

Fig.21.Velocity histories of the guided trajectory (100 cases).

Fig.22.Local flight-path angle histories of the guided trajectory (100 cases).

6.2.2.Monte-Carlo simulations analysis

To further test the validity and robustness of the guidance algorithm in this study,10000 random dispersed cases from Table 6,Table 8 and the initial flight state deviation given above are used to carry out Monte-Carlo simulations.100 simulation results are randomly selected from 10000 simulations.The three-dimensional trajectory,velocity curve and local flight-path angle curve of the guided trajectory are obtained,as shown in Figs.20-22,respectively.Fig.23 and Fig.24 show the boxplot of the absolute values of the longitudinal,lateral and impact deviations of the robust guided trajectory and the non-robust guided trajectory,respectively.The maximum value,3σ value and average value of the impact deviation of the robust guided trajectory are 10.2 m,7.5 m and 3.0 m,respectively;whereas the maximum value,3σ value and average value of the impact deviation of the non-robust guided trajectory can reach 63.8 m,32.0 m and 8.1 m,respectively.Hence,the robust guidance algorithm can overcome the interference caused by the DCS parameter deviations to a certain extent.In addition,the impact point accuracy of the unguided trajectory is counted in this study,with the maximum deviation of 46549.8 m and the average deviation of 14473.8 m.The guidance algorithm can solve the guidance problem of the HMPBM after the HMP to a certain extent.

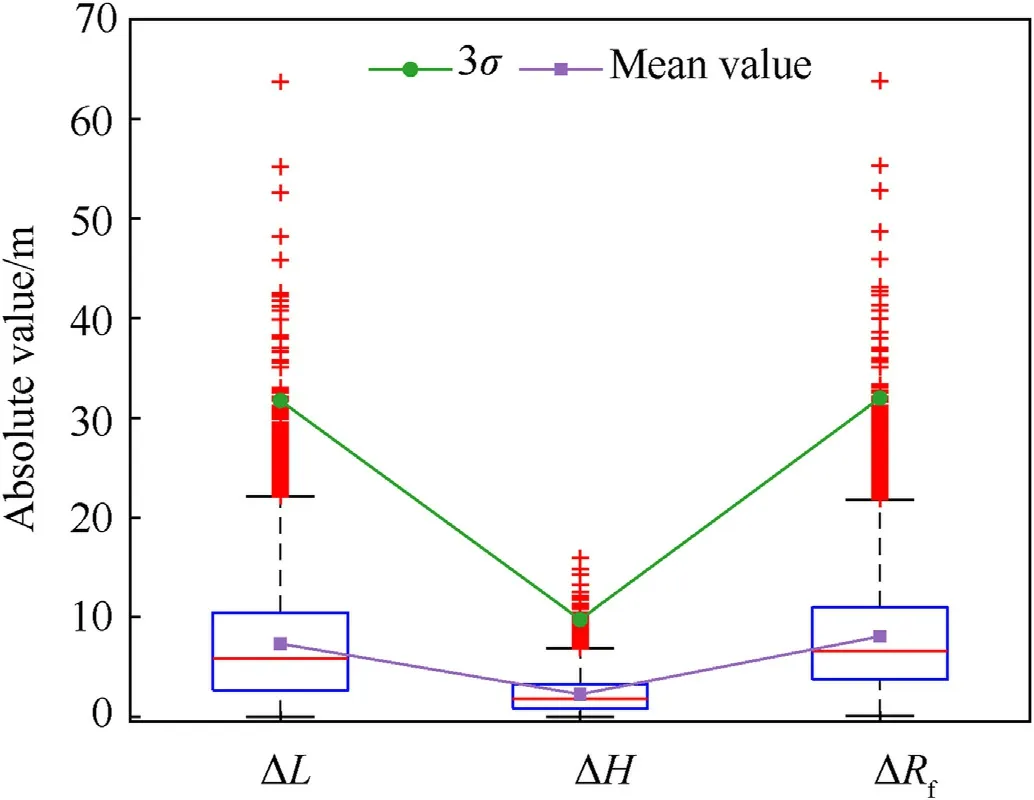
Fig.24.Boxplot of the impact deviation of the non-robust guided trajectory.

6.2.3.Computational complexity analysis of the proposed guidance algorithm

From Algorithm 3,the main factors affecting the time consumption of the guidance algorithm are the solution of ΔWg(i.e.Algorithm 2).At the same time,the time consumption of Algorithm 2 is mainly composed of the time consumption of the IPP and the time consumption of solving the impact deviation.To verify the iterative efficiency,the number of IPPs required in each guidance period is counted in 10000 Monte-Carlo simulations,as shown in Table 9.

Table 9Number of IPPs required in the guidance period.

As shown in Table 9,the IPP algorithm in the first guidance period is run up to 10 times,that is,Algorithm 2 needs 3 iterations at most.Other guidance periods only need to run the IPP algorithm four times at most,that is,Algorithm 2 only needs to be iterated one time at most to obtain ΔWg.At the same time,as shown in Fig.11,the IPP algorithm with double data type takes 2.374 ms to run once;thus,the run time of Algorithm 2 is extremely small.To further verify the rapidity of Algorithm 3,the STM32F407 single-chip microcomputer is applied as the experimental platform,and the double data type is used.In the case of one iteration of Algorithm 2 in one guidance period,the time consumption of each module of Algorithm 3 is shown in Fig.25.The total time consumption of Algorithm 3 is about 9.936 ms,which is relatively small compared with the guidance period time and can meet the needs of online guidance algorithm.In addition,the time consumption of the IPP is the key to restricting the calculation speed of Algorithm 3.Therefore,further improving the speed of the IPP will help improve the real-time performance of Algorithm 3.

Fig.25.Run time pie chart of each module of Algorithm 3.

7.Conclusions

In this study,aiming at the problem of precise guidance for HMPBMs after the HMP,an online guidance algorithm based on the IPP using the SL method is established,which provides a good reference for solving the problem to a certain extent.The conclusions are stated as follows:

(1) A guidance framework based on the IPP is established,which is composed of an SL-based IPP module and a robust guidance parameter calculation module.

(2) Aiming at the requirement of the IPP in the guidance algorithm design process,an IPP algorithm based on SL is established.To improve the prediction accuracy,three NN models are established to predict three components of the impact point.The height,latitude,velocity vector in themxnynzn-CS,local flight-path angle,velocity azimuth angle and velocity are introduced as NN inputs.To further improve the prediction speed,the sigmoid activation function is improved.The simulation results show that the SL-based IPP model has high prediction accuracy and short time consumption.After improving the sigmoid function,the time consumption of the NN is further reduced by 46.3%.

(3) Aiming at the problems of nonlinear,strong coupling,multiconstraint and fault-tolerant requirement in the guidance parameter calculation of the HMPBM,the sensitivity coefficients are calculated online based on the IPPNNM algorithm,and a fast iterative algorithm for guidance parameters is proposed.On the basis of the apparent acceleration of the INS output,the calculation method of the guidance parameters in the case of DCS parameter deviations is designed.The simulation results show that the parameters in the first guidance period takes three iterations at most to solve,and only one iteration at most in the other guidance periods.In addition,the 3 σ error of the guidance algorithm is 7.5 m.

(4) The STM32F407 single-chip microcomputer is used as the experimental platform to test the calculation efficiency of the guidance algorithm.The simulation results show that it takes about 9.936 ms,which indicates that the algorithm has a good real-time performance and a certain engineering application value.

This work only studies the online guidance algorithm of the HMPBM.In view of the serious error accumulation of the INS in the later stage of the navigation,the improvement method of hit accuracy must also be investigated,considering the INS error and guidance algorithm error simultaneously,which will further improve the engineering application value.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This research is supported by the National Natural Science Foundation of China (Grant No.62103432),and also supported by Young Talent fund of University Association for Science and Technology in Shaanxi,China(Grant No.20210108).