SUNDER:Self-organized grouping and entrapping method for swarms in multitarget environments
Yutong Yun ,Zhun Fn ,Xiomin Zhu ,c ,Li M ,c ,Ji Ouyng ,Weidong Bo ,Ji Wng ,Zhojun Wng
a College of Systems Engineer,National University of Defense Technology,Changsha 410073,China
b School of Electrical and Information Engineering,Shantou University,Shantou 515063,China
c Strategic Assessments and Consultation Institute,Academy of Military Science,Beijing 100097,China
Keywords:Swarm robots Local information Gene regulatory network Swarm grouping Trapping pattern Confined multitarget environment
ABSTRACT For swarm robots moving in a harsh or uncharted outdoor environment without GPS guidance and global communication,algorithms that rely on global-based information are infeasible.Typically,traditional gene regulatory networks (GRNs) that achieve superior performance in forming trapping pattern towards targets require accurate global positional information to guide swarm robots.This article presents a gene regulatory network with Self-organized grouping and entrapping method for swarms(SUNDER-GRN) to achieve adequate trapping performance with a large-scale swarm in a confined multitarget environment with access to only local information.A hierarchical self-organized grouping method (HSG) is proposed to structure subswarms in a distributed way.In addition,a modified distributed controller,with a relative coordinate system that is established to relieve the need for global information,is leveraged to facilitate subswarms entrapment toward different targets,thus improving the global multi-target entrapping performance.The results demonstrate the superiority of SUNDERGRN in the performance of structuring subswarms and entrapping 10 targets with 200 robots in an environment confined by obstacles and with only local information accessible.
1.Introduction
Swarm robots use swarm intelligence to carry out complex tasks,such as regional search and disaster rescue [1].Simple,flexible,and modular interactive robots are poised to become common in complex systems[2].Swarm intelligence has its origins in swarm behavior,which involves self-organization and stigmergy.Many seemingly chaotic structures exhibit implicit intelligence resembling swarm behavior,e.g.,bird flocks,fish schools,wolves’packs,and slime mold foragers [3].Thus,the underlying intelligence on biological collective behaviors has drawn considerable interest from researchers..
Recent studies have concluded that swarm robots can attain swarm intelligence by learning biological collective behaviors found in nature.Over time,several gregarious species have evolved to move in specific swarm patterns,e.g.,seashells flocks,fish schools[4],bird flocks,and ant colonies[5-8].These patterns help them escape their natural enemies and reduce the mortality of their populations.Swarm behaviors involve self-organization and local interaction.Self-organization is a spontaneous process in which some form of global order or coordination emerges from local interactions among components in a fully decentralized or distributed manner [9,10].Exchanging local information can not only compensate for individual deficiencies but also enhance individual spatial comprehension.However,many bio-inspired swarm algorithms violate the constraints of the locally interactive characteristic and attempting to obtain intelligent performance via a global planner or controller,e.g.,hierarchical gene regulatory network (H-GRN) [11]incorporates cell mechanism into a multiagent system,which empowers agents to collectively trap targets.The global influence of targets on the environment is consistently calculated and updated.In addition,the predictive positions for entrapping were sampled by Non-Uniform Rational B-Splines(NURBS)[12]and the underlying scheduling scheme controlled by a planner was required between robots and these positions.Such underlying centralized planning methods and the utilization of global information restrict the generalization and practicability of a multiagent system.
Grouping,a crucial concept in multitarget problem-solving,is a direct approach for decomposing multitarget problems into subswarms to harvest better global performance.A reasonable grouping strategy can help swarms achieve accurate and rapid spatial grouping and ensure the execution of potential subtasks.Unfortunately,the grouping of a robotic swarm to probe an unknown dynamical environment is still in its infancy.Most traditional grouping methods are based on known global information,which accounts for the limited application in outdoor or communication-restricted environments;however,some of them are based on local information and cannot group enough members in a swarm to satisfy the requirement of certain specific tasks.There have been studies on swarm splitting that have achieved grouping effect by designing a splitting controls scheme,which focuses on the cohesiveness before and after splitting and merging instead of optimal quantitative grouping.In this study,we propose a Selforganized groUping aNd EntRapping method for a swarm with a hierarchical gene regulatory network (SUNDER-GRN),which improves the performance and practicability of traps in confined multitarget environment as compared to traditional GRNs.
The remainder of this manuscript is organized as follows.Section 2 reviews related work.Section 3 introduces the SUNDER-GRN model,including a hierarchical self-organizing swarm grouping algorithm(HSG)and a local information-based GRN for multitarget environment with obstacles.Section 4 describes the experimental setup and evaluation indexs.Section 5 details the experimental results and the comparison with other grouping and trapping methods.Section 6 summarizes the study and discusses the limitations as well as future scope.
2.Related work
There are many bio-inspired methods to study swarm pattern formation,at both the macroscopic level and microscopic level[3].At the macroscopic level,researchers have studied natural swarm behaviors through swarm models,such as the structured approach and behavioral approach.The structured approach emphasizes that a swarm should maintain a specific structure with individual members separated by distance,such as the leader-follower model[13]and the virtual structure model[14].In contrast,the behavioral approach focuses more on individual behaviors and overall performance in a swarm,such as the flocking model[7],potential field[15],and consensus-based control [16].At the microscopic level,researchers have also taken inspiration from the multicellular mechanism-inspired pattern formation.Multicellular organisms provide the most impressive examples of morphogenesis wherein massive groups of cells combine and actively collaborate during embryonic development to build complex tissues and organs [17].Cell regulation,i.e.,division,differentiation,and apoptosis,occurs through morphogens or similar functional proteins.Researchers have encoded this procedure into multirobot systems to develop a series of bio-inspired swarm models,e.g.,morphogen diffusion[18],reaction-diffusion model (RD) [17-19],gene regulatory networks (GRNs) [11,20,21],and chemotaxis [22].These models generate morphogens or protein concentration fields to guide the swarm robots to form patterns along gradients of the morphogens or protein concentration.Slavkov et al.[17]summarized two types of processes to form swarm patterns in a real robot system:(1)Topdown control and (2) local self-organization.They assumed that swarm robots should behave in a fully distributed control scheme to emerge intelligence;however,they simply explained some sketchy rules for the direction of swarm movement from an original pattern to a final one,but failed to explain what shape the pattern formed by the swarm robots would looks like.At present,there is still a long way to go in terms of morphing into a particular shape in this fully distributed control scheme.As for GRNs,they possess huge potential in forming a particular shape compared with those foregoing microscopic swarm models,because the target-based predictive pattern for the trap is completely generated instead of generating predictive points for swarm aggregation in those models.
In biological organisms,the regulation of interactions among genes,proteins,and morphogens is encoded into the genome of each cell.In a multicellular organism,all cells shave the same genome,but changes in the arrangement of the activated and silenced genes differentiate the behavior and functionality of each cell and regulate the expression of genes.Proteins are also products of genes and are responsible for signaling,sensing,actuation,bounding,etc.This process is governed by the GRN,which is a model of genes,and the interaction of gene products describing the dynamics of gene expression [23].The GRN offers a standard framework to study swarm intelligence as an aspect of the microscopic theory,which reveals that every trait expression emerges from the corresponding gene,and every individual possesses the same genetic sequence.Entrapping targets is a complex task for swarm because it demands higher requirement than collective aggregation or flocking pattern.Guo et al.[11,24]drew an analogy between a robotic system and cell mechanics.With this analogy,they utilized the hierarchical GRN (H-GRN) to depict a robotic system,which resulted in the successful pattern formation for trapping using the non-uniform rational B-spline [12]to obtain discretized predictive trapping positions.Oh.et al.[25]improved the efficiency and robustness of the H-GRN in replacing accurate predictive positions with equally decomposed segments,integrating all the pieces of the same curvature.Then,they proposed an improved H-GRN,named EH-GRN,to add avoidance to the environment using a simple neural network.Peng et al.[26]replaced the NURBS in H-GRN with the interpolating implicit function (IIF)methods to control different pattern generation,e.g.,the spanner shape and bird shape.Besides,they considered a scenario where a swarm of robots must traverse a tunnel to entrap a target.Zhang et al.[27]further replaced the IIF with the radial basis implicit function (RBIF) to guide the swarm to split and merge when the swarm frontally encountered an obstacle.Wu et al.[28]proposed a cooperation-based GRN (C-GRN) to achieve swarm collective entrapment with partners that were transformed from obstacles in a multi-target confined environment.Hu et al.[29]proposes a cooperative hunting scheme based on the multi-target k-winnertake-all (k-WTA) algorithm and the wolf-pack-particle-based model to achieve task allocation and entrap targets in dynamic environment.Unfortunately,these trapping methods based on traditional GRNs are heavily dependent on global information such as exerting task allocation and planning,which restricts the practicality of entrapment in an unknown environment.For applying trapping methods to decentralized multi-agent system in real environment,some studies based on a small-scale swarm to entrap few targets were proposed.Hu et al.[30]proposed an equaldistance surrounding control method for second-order nonlinear multiagent systems (MASs) to entrap two moving targets by four real USVs,but the method rigidly require the swarm to move toward the center of targets,and the swarm is required for a rigid rectangle pattern by maintaining an angle of 90°between any three robots,which makes it hard to perform well in scenarios with very scattering targets and to be scalable to large scenarios.Wang et al.[31]proposed an adaptive grouping and entrapping method for flocking systems (AGENT) to achieve swarm adaptive grouping based on local environmental information and develop a modified potential field method to entrap a target.The method that was finally implemented on E-puck 2 platform (wheeled micro robot platform) demonstrated 10 swarm robots could entrap 2 moving targets.Nevertheless,it was hard for AGENT to adjust parameters to adapt to different entrapping requirements,because the number of robots for a trapping formation and swarm moving control shared the same set of parameters,i.e.,changing one had a huge impact on the other.There was no doubt that the point strongly influenced the scalability and flexibility of AGENT.It can be concluded that global information-based GRNs restricts their extension in real world,and implementing local information-based trapping methods on a large-scale swarm to entrap more targets is still a challenge.
Grouping is crucial for improving the overall efficiency of tasks for the swarm in a multitarget environment because the decomposition of tasks from a swarm to subswarms benefits tackling the multiple targets by turns.There are some potential multitarget tasks scenario,such as joint defense[32],exploration[33],trap[11].Unfortunately,there are few studies about swarm robot grouping,especially in decentralized grouping and self-organized grouping.Some grouping methods revolve around global information,such as global grouping optimization and machine learning-based clustering.These methods require that all robots' positional information must be received messages by a centralized processor from God's point of view,and the amount of classification quantity should be set in advance.Al-Obaidy et al.[34]utilized the genetic algorithm to achieve the balanced centralized grouping between center nodes and normal nodes.Although this method guaranteed fewer grouping centers,it failed to consider the robots' communication load in the process of grouping.Lee et al.[35]grouped robots based on the concept of theK-nearest neighbor that requires global spatial positional information.Wang et al.[36]proposed a chainedgrouping method to achieve swarm grouping only using local information,and a redundant mechanism for those agents that failed to be grouped to rejoin in one of these group.Roy et al.[33]utilized the virtual elliptical regions to guide the swarm to explore multiple unknown areas,which enables the swarm to decide the number of the subswarm according to the width of the passages.Wang et al.[37]developed a grouping-based optimization method based on traditional K-means method to achieve swarm multi-letter pattern formation in confined environment.Some grouping methods based on achieving grouping consensus by local interaction between adjacent agents are time-consuming,and the robots must hold specific opinions in the initialization phase to help them determine the convergent direction of consensus.Cruz et al.[38]proposed a self-organized clustering algorithm to achieve consensus on a maximum of four opinions for small-scale robots in a static environment.Scheidler et al.[39]proposed thek-Unanimity rule to enforce consensus between robots on dualistic opinions between choosing either a long or short path,which emulates the process of ants transporting food to their hills.The other grouping methods based on the change of swarm pattern by adjusting controller parameters rely on local interaction between surrounding agents and have fast grouping response,but it is hard for these methods to accurately control the number of agents in each group.Chen et al.[40]achieved a different number of subswarms grouping and splitting via controlling the magnitude of a Gaussian-like repulsive interaction between agents,while this control law is suited for the pattern formation of the swarm because the synchronicity of splitting cannot play a role in an unknown environment well.Wang et al.[31]proposed an adaptive decision-making method(ADM)to achieve self-adaptive even grouping effect in the process of swarm entrapping targets.Swarm robots utilized local information to calculate a weighted value (Seq) to make decisions on their own subswarm numbers.It can be concluded that known global information-based grouping methods cannot be applied to some harsh or uncharted outdoor environments without GPS guidance and global communication,and current local information-based grouping methods are faced with time-consuming and rough grouping problem.
Many real multiagent systems merely allowed for the utilization of the agents’ local information that has emerged as some specific function.Except for the research ([30,31,39]) mentioned before,Rubenstein et al.[41]invented a minimalistic,low-cost robot called the Kilobot.It was applied to the study of morphogenesis to generate the desired swarm shape,e.g.,starfish [42].The Kilobots navigate by vibrating two small legs,measure the distance by toeto-toe infrared detection,and communicate with each other at a short range.Each robot receives message packages composed of 9 bytes broadcasted twice per second.This technology is considered a breakthrough in the field of swarm robotics because swarm pattern formation transformation could be achieved on such a large scale on a real robotic platform.Slavkov et al.[17]proposed an improved RD model and a neighborhood-based distributed control to simulate morphogenetic processes with 200 kilobots.However,the Kilobot can neither self-localize nor identify the location of neighboring robots.Shirazi et al.[43]constructed a relative coordinate system to break the limit of localization in Kilobots and a morphogen diffusion model to guide the swarm to follow a target.Scheidler et al.[38]utilized 10 micro wheeled robots named epuck2,only allowed to interact and change their own opinions at short range in the base,to achieve convergence of dualistic opinions.Gao et al.[44]took the lead in achieving obstacle-free UAV formation in a bamboo forest without using global information.These studies reflect real large-scale multiagent systems,especially those exerted in an outdoor environment,are expected to utilize local information instead of global information to accomplish complex collective tasks,which can bring stronger robustness and practicability.
Our proposed model makes multiple contributions to multitarget trapping with a large-scale swarm in confined and local information-based scenario,the details are as follows:
(1) A gene regulatory network with Self-organized grouping and entrapping method for swarms (SUNDER-GRN) is proposed to improve multitarget trapping performance for a largescale swarm on confined local information-based environment.By a combination of swarm grouping and modified control scheme,a large-scale swarm can actively sunder and entrap different targets in a self-organized way.
(2) A hierarchical self-organizing grouping method (HSG) is introduced to ensure that each robot in the swarm leverages its neighbors' resources to group as many partners as possible,notwithstanding a limited communication range.HSG develops a distributed swarm grouping strategy with a combination of the number of the neighbor's neighbors and distance,which lessens the uncertainty of grouping pattern and the communication pressure of grouping nodes,compared with completely distance-based grouping methods.In addition,a target-driven mode is also implemented in HSG to ensure that the swarm can flexibly group members when they encounter a newfound target on site instead of planning in advance of time.
(3) A gene regulatory network with local information is introduced to enhance multi-target trapping performance for a large-scale swarm in confined environment.First,a relative coordinate system is established to generate trapping patterns,which eliminates the rigid demand for global information in the process of GRN.Second,a modified decentralized control scheme combined with HSG is used to accelerate swarm to entrap different targets and remove the disturbances that randomness of relative coordinates causes when relative positional information is updated,which makes subswarms hurdle the concentration abyss between different targets generated by GRN.
3.Self-organized grouping and entrapping method
In this section,a local GRN model with self-organized grouping and entrapping method (SUNDER-GRN) is introduced to achieve trapping task for swarm in a multitarget environment.To satisfy far-ranging and practical application scenarios,the GRN solely relies on local communication in the overall phases of the task,including grouping and entrapping.The overall framework of SUNDER-GRN has three modules(shown in Fig.1).(1)Informationcollection module.This module collects external information for each agent,including the targets and the environment.The target for swarm trapping tasks contains forest fire,criminal,biochemical/radiative stuff,emergency rescue,etc.The swarm trapping tasks is not only for surrounding the target and making it in a disadvantageous state,but also collectively assessing or measuring the influence of hazard harm.The environment reflects the feasible spatial positions for agents,e.g.,the swarm needs to avoid different obstacles,such as a tree,mountain,crowd,or narrow path(shown in Fig.1(a)).(2) Target-trigger Grouping module.This module contains a hierarchical self-organized grouping algorithm(HSG)for a swarm.The HSG,a neighbor-distance mixed grouping method,is suitable for distributed multiagent systems because the algorithm is just triggered at the timing when the swarm firstly observes a target,and the grouping process that is similar to the distributed controlling,is completely driven by the local interaction between agents (shown in Fig.1(b)).The neighbor-distance mixed characteristic results in the compact spatial formation of the subswarm,which enables the subswarm to separate and withdraw from the original swarm.(3) Pattern-formation module.This module introduces a local information-based GRN using a relative coordinate system to form a trapping pattern toward targets.The relative coordinate system supplies the possibility of entrapping targets for the swarm on condition that the swarm just possesses local information,i.e.,the swarm can entrap the target in a self-organized way after unexpectedly encountering a target in an unknown environment.The information of the target ceaselessly received and delivered within the swarm is utilized to generate a local trapping pattern,and an improved collective control scheme is leveraged to lessen the influence of differences between mutual patterns,which can easily cause local swarm aggregation and thus obstruct the formation of trapping pattern(shown in Fig.1(c)).Next,we explain the SUNDER and GRNs through cell growth in organisms.The cell mechanism is analogous to multirobot systems in that multiple gene segments control the cell activity by translating the related protein like a multirobot system orders the constituent robots to adjust the parameters related to the control of their motion.Traditional GRNs are divided into two phases: pattern generation and pattern formation.The pattern generation phase calculates the predictive region which decides on the basic shape of formation,then the pattern formation phase controls agents to form the practical pattern guided by the predictive positions.
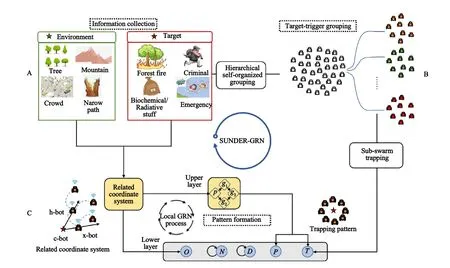
Fig.1.Model of the SUNDER-GRN.
The previous studies emphasize the pattern generation and the methods to sample positions for agents from the pattern;however,they disregard two important limitations in responding to a multitarget scenario: 1) the protein gradient around one target generated by a GRN can be easily trapped in a local optimum,making it difficult for the agents to shift from one target to the other as soon as they have inched toward either target.Hence,traditional GRN performs poorly in the multi-target scenario as the robots could be preoccupied with one of the targets unless dispatching agents in advance.Fig.2 demonstrates the concentration generated by the H-GRN in a dual-target environment.Except in zones where robots must maintain a safe distance from the targets,the robots are attracted to the regions with a protein concentrationggreater than the thresholdgth.This mechanism is beneficial to converge robots to regions with higher protein concentrations;however,it could create a concentration abyss (yellow region in Fig.2),which means in that the robots cannot avoid a concentration tie between the two targets.In this case,the robots lack the competence to move from the high concentration regions of one target's vicinity to another’s;2) the control scheme has the same coefficients towards different targets,leading to the same tendency within targets in formation phase and insufficient sensitivity for agents to react.Even if just increasing the coefficient to one of certain targets,it is also hard to control an accurate number of agents to swerve.Thus,the sensitivity of a GRN between multiple targets for agents should be improved.In addition,traditional GRNs utilize excessive global information to regulate agents' behavior,which restricts GRNs from developing in practical scenarios.For solving these problems,we proposed the SUNDER-GRN to improve the trapping performance of swarm in multitarget scenarios including a hierarchical self-organized grouping method and a local information-based GRN model.

Fig.2.Analysis of gene regulatory networks in two target concentration condition.
3.1.Hierarchical self-organized grouping algorithm
Grouping facilitates handling complex multi-target problems for swarm via decomposing the tasks into many sub-tasks and simultaneously sundering the swarms into several subswarms.Although most of the research surrounding global information plans potential task objectives and group optimal subswarms,there is an application gap between theories and reality.In a complex and uncharted environment,the swarm often relies on limited and unstable communication and even lack artificial centralized control.Therefore,the grouping method must adhere to two conditions: 1)Limited communication: either communication capacity or communication distance restricts swarms from receiving periodic information of from all members.In our study,limited communication mainly represents swarm robots can send and receive message from their neighbors within the range of a limited communication distance.The number of neighbors should dynamically change as the surrounding environment changes.Generally,researchers assumed that,to stay connected with most of its neighbors,each robot must maintain communication with at least another robot.If one robot loses contact with any other robot in the swarm,it has departed from the swarm.This assumption explains the lower bound of swarm communication;however,uninterrupted communication between a robot and its neighbors cannot be guaranteed.2) Self-organization: the limited communication scenario cannot support artificial centralized control to plan whatever the swarm needs at any time.The swarm operator shall not predesignate an organizer or arrange a new one to group the swarm.Thus,a high degree of autonomy is expected,that is,the swarm must have competence for grouping itself in self-organized way.
Therefore,to satisfy these conditions,we proposed the hierarchical self-organized grouping algorithm (HSG) shown in Fig.3.Inspired by a real work scenario of an unmanned device,the individuals in the swarm fully utilizing local information adopts distributed grouping method to form subswarms,and the grouping process is only activated the moment when the swarm observes a target and the first-order organizer,which first observes the target starts to muster partners.Based on the grouping strategy of a combination of the neighbors’ neighbors and distance,both the individual that possesses the maximum number of neighbors’neighbors and the individuals that are closest to the organizer are mustered to as the first-order partners.The individual that possesses the maximum number of neighbors’ neighbors will be the second-order organizer to continue the grouping process until the expected grouping numberNegnis reached.The grouping process is visually exemplified in Fig.3.The swarm (in ungrouped status)scattering onto the scenario encounters a target,then activates the first-order organizer that first observes the target and starts to muster c partners (shown in Figs.3(a)-3(c)).The second-order organizer starts to muster new partners in Fig.4(d).The thirdorder organizer continues the grouping process in Fig.3(e).The only one ungrouped member left is mustered in Fig.3(f),which reveals one grouping terminal when the residual number of ungrouped individuals is fewer than c (c =3).

Fig.3.Hierarchical self-organized grouping mechanism: (a) Initial status;(b) One robot turns to the first-level organizer when observing one target;(c) c ungrouped robots are mustered by the first-order grouping organizer(c =3),and the maximum number of neighbor of neighbors(NNs =4) is going to be the next-order grouping organizer to muster potential partners (with dashed line) within the communication range of Rc;(d) c ungrouped robots are mustered by the second-order grouping organizer (c =3),and the maximum number of neighbor of neighbors(NNs =5)is going to be the next-order grouping organizer to muster potential partners(with dashed line)within the communication range of Rc.(e)-(f): Rest of the robots are grouped by other subordinate organizers.

Fig.4.Traditional grouping methods:(a)Greedy grouping forces close neighbors to join the swarm;(b)Chained grouping seeks the nearest member to join the swarm;(c)Adaptive decision-making grouping makes individuals decide their own group by observing a target.
Next,to conveniently describe the spatial grouping of swarm robots and algorithmic pseudocode,we established an abstract model of swarm robots.We assumed that U was the set of swarm robots and K is the set of targets.Each robotuis a tuple{s,id,g,m,n,c,dis,org},where(1)s represents the current grouping state,(2)id is the unique identification number,(3) g is the group number,(4)mis the expected partner number of the group,(5)nis the number of neighbors,(6)cis the maximum mustering number for an organizer,(7)dis is the relative distance between the neighbors and the robotu,and(8)org is the extra grouping switch status for the organizer.The robots'states were“ungrouped”,“grouped”,and“organizer”,which are denoted ass={sung,sgro,sorg}.States “ungrouped” and “grouped” indicate if a robot becomes a member of one of the groups.“Organizer” indicates the robot becomes a special grouped individual and will have been mustering ungrouped neighbors by the end of the current grouping process.uvdenotes the focus robot v that is a starting point of HSG in Algorithm 1,and Tvdenotes the robot v's neighbors listed in increasing order of the distance between the robot v and its neighborstores the estimated distance between robot v and its neighbors.Nvdenotes the robot v's neighbor list.nin the descending order of the number of neighbors of its neighbors.Negndenotes the expected grouping number.Owing to the distributed characteristic of HSG,Algorithms 1,2,and 3 mainly exhibit the grouping process around the robot v and its neighbors.The flowchart of the HSG algorithm is introduced below.

Algorithm 1Hierarchical Self-organized Grouping Algorithm
In the initialization phase,all robots’ status was reset to the original ungrouped status.In the operating phase,the swarm initiated the grouping process when targets were observed by any ungrouped individual of the swarm and the first-order organizer would be chosen to mustercneighbors that stayed at ungrouped status(Algorithm 2).The triggering condition on grouping was fully customized to enhance the self-organized competence and flexibility of the swarm in a multi-target environment without global information and a central controller.

Algorithm 2Become First-order Organizer

Algorithm 3Confirm Next-order Organizer
If the current first-order grouping process ends and the grouping goal cannot be reached,algorithm 3 would be triggered to choose the next-order organizeruq,and the new partners would be mustered.The next-order organizer was confirmed by finding the robot that possessed the maximum number of neighbors of the upper-order organizer's neighbors (NNs),so that there was a greater chance of satisfying the expected grouping number.If there were multiple alternative next-order organizers Q (Q⊆Tv),the distance-based priority strategy would further confirm the residual partners from other upper-order organizer's ungrouped neighbors,that is,the closest robot with the most NNsto the upper-order organizer would finally be the best next-order organizer.This strategy promotes the spatial aggregation of the group,which benefits the pattern and following collective movement of the swarm.The self-organized grouping process was probably to yield iteratively,just as branches grow in nature.The grouping method need to constantly consider the matching relation between expected grouping numberm,maximum mustering number for an organizercand the number of neighbors # Tv,as Algorithm 1 shows.Finally,the output W represents the robot set in which those robots grouping numberu.g is equal touv.id,that is,the new subswarm shares the same group number from the first-order organizer.
The terminal of the whole grouping process should be discussed.In fact,no matter how hard algorithms try,the actual grouping number could be less than the expected one.When there were no ungrouped neighbors within the communication range of an organizer,the organizer would be the last member of the group,and the grouping process would stride to an end.In a complex environment,the swarm was still likely to disperse into several groups activated by different targets;thus,the grouping process could be carried on simultaneously within the group at any moment.
3.2.Gene regulatory networks with local information
In the swarm robotic system,it is a practical attempt to localize themselves solely through local communication with neighbors.Usually,one common assumption in many swarm algorithms is that some agents,as the anchor or beacon nodes,could obtain predetermined positions or possess global positioning systems like GPS,let alone those algorithms that all agents could attain their positioning information at any time.On one hand,these algorithms will not function properly without the support of global information.The process of swarm activities being planned from God's perspective,on the other hand,violates the original intention in swarm robotics that swarm intelligence should emerge from agents' behaviors exclusively through local interaction.Gene regulatory networks (GRNs),which are inspired by cell mechanisms,are an effective approach for swarm robots to entrap targets.The swarm robot system generates and forms specific geometries by regulating the protein concentration and generating the relationship between targets and robots through a simulation of the activities between genes and proteins.The H-GRN proposed by Jin and Guo [24]achieves a hierarchical structure to form a swarm pattern.The H-GRN can generate protein concentrations according to information on targets and guide the swarm robots to congregate in the region with the high concentration,assisting in the formation of a specific shape.However,the global predetermined positions towards trapping patterns are used by the agents' controller and ceaselessly updated and evolving with time,which helps agents follow targets and form the expected pattern.
3.2.1.Establish relative coordinate system
For swarm robots,gene regulatory networks with only local information should be constructed to exert agents in more practical situations.As a result,a related localization coordinate system should be created.According to the target-triggered hierarchical self-organized grouping algorithm above,we could determine the first order organizer as the center of the coordinate system,i.e.,a center bot,because the one gets closest to the target.First,the center-bot propagates the ID of its closest neighbor.Thex-axes of the swarm coordinate system are determined by the closest neighbor,dubbed thex-bot.Oncex-bot has received a message from the center-bot and identified itself as thex-bot,it sets its position to(dcx,0),wheredcxis the distance between thex-bot and center-bot.Then,it changes its localization status to determine and propagates its position.Once this is done,one robot can be chosen as theh-bot by the center-bot from those that can see thex-bot.Theh-bot should satisfy the condition below where theh-bot,the center-bot and thex-bot maintains an equal distance from each other as possible.
wheredcxanddciare the distances from the center-bot to thex-bot and roboti,respectively,anddixis the distance between robotiand thex-bot.In this part,the movements of robots could eradicate possible flip ambiguity of the coordinate system and correct it to right-handedness.Consequently,theh-bot can be assumed on the top of thex-axis,and the relative position can be calculated as(dhccos(α),.
wheredhxis the distance betweenh-bot andx-bot anddhcis the distance betweenh-bot and center-bot.Both of them are measured and calculated byh-bot.
3.2.2.Propagate relative position
Other robots that can communicate with the three can compute their relative positions once three robots(center-bot,x-bot,andhbot) construct a local coordinate system.When each robot calculates its relative position,it propagates its estimated positions to its neighbors,which accounts for the comprehensive propagation of local position information through the subswarm.As the subswarm constructed by HSG also obeys the characteristic of local interaction,i.e.,there always exists at least one fellow of the subswarm belonging to each robot's neighbors,all members of each subswarm can receive its neighbors' messages about relative position.
3.2.3.Dynamics of GRN
According to the relative position of the target,the swarm robot can form specific geometries by regulating the protein concentration.The relationship is erected between targets and robots through a simulation of the activities between genes and proteins.The dynamics of GRN contain the trapping pattern generation(upper Layer) and the trapping pattern formation (lower layer)shown in Fig.(1).During pattern generation,each organizing robot will simulate the following dynamic equations (Eqs.(3)-(8)) to produce the chemical concentrations needed to create the desired pattern.
The grouped organized robots have onboard sensors that can either determine the target's relative position within the range of detection or can learn it from the nearby organizing robot that comes from the same group.Where γj,a scalar value,represents the environmental inputs of these dynamic equations,holding a positive constant value where targets are located.∇2,a Laplacian operator,can be viewed as the diffusion process in a biological system and is described as the second-order derivative ofpjin the spatial domain.pjdenotes a protein concentration produced from thejth target's environmental input (γj) andpdenotes the integrated protein concentration fromNttargets that the organized robot directly observes and indirectly receives from neighbors within the same subswarm.g1,g2andg3denote the protein concentrations.g3,regulated by bothg1andg2,is the morphogen gradient defining the final target pattern.The sigmoid function,also called the logistic function,is used for the output of the hidden layer neurons,and takes values in the range(0,1),which maps a real number to the interval(0,1).ρ,θ1,θ2,and θ3are a positive constant.The relative coordinate system is constantly updated as each subswarm moves,therefore,a potential coordinates drift could occur,jeopardizing the precision of the trapping formation.The drift could cause the jumping of concentration near a target.Also,agents are sensitive to the gradient of concentration around themselves.As a result,some agents could be caught in an abnormal state,such as pacing back and forth around the regions where the concentration change jumps.Some agents may congregate together somewhere instead of forming a trap pattern.Thus,an improved controller(Lower layer)is designed to refine this situation and the swarm can adjust itself out of the abnormal state.The controller contains five elements: Target (T),neighbor (N),Pattern (P),Density(D),and Obstacle (O).
(1) Target: For following or repulsing targets,a linear distancedependent velocity term with a maximum safe distanceRtarget,under which agents start to follow the designated target that matches their grouped status or repulse other targets.Thegth target represents the labeled target by the subswarm tuple.Here,the swarm cannot attain and perceive global information on targets,so thegcan be numbered by the unique ID of the first organizer in the group.The direction from theith robot to thejth target can be calculated byrepresent the position of theith robot and the position of thejth target.Ntrepresents the number of targets within the radius ofRtarget.
(2) Neighbor: A suitable distance between agents and their neighbors is necessary,therefore,a vectorial sum involving the neighbors with a safe distanceRneighborsupplies effective avoidance between each other.Ncrepresents the number of neighbors within the radius ofRneighbor.
(3) Pattern: A delicate probe to guide agents to the trapping pattern directs the maximum gradient of concentration around themselves calculated in Eq.(6).Guiis the concentration of the location position of robotui.G′is a collection loading up the roboti's ambient concentration of the position vjrestricted in a range of radiusRpattern.The maximum concentrationcalculated in Eq.(13)is used to guide robotuito go forward the maximum gradient towards the desired trapping pattern in Eq.(12).
(4) Density: An effective strategy to diminish destructive aggregation is to construct self-adaptive density guidance,which brings extensive swarm shape whenever the swarm desires to deploy a collective formation,especially a largescale formation.Overmuch aggregation could make unavoidable repulsion between robots and then trigger various degrees of collision or loss.Density is to guide robots to the direction where fewer neighbors locate in.Ndrepresents the number of neighbors within the observation radiusdobs.We design a permanent density effect between neighbors and take advantage of a relatively small weightpdensity1to control,while a relatively great weight is used to help robots escape from disturbance caused by the relative coordinate system when robots approach the desired target.Because the relative coordinate is being updated and the source of the coordinate system is mobile,the deviation of the target's relative coordinate between adjacent times exists.The deviation is so little that the swarm could still bypass it to approach to the target.However,the deviation possibly causes the perceived position of the target to bounce on its left and right sides repeatedly,which causes swarm mobility disorders,e.g.,swarm gets stuck and assembles on the desired targetkg’s one side instead of trapping.The relatively great weightpdensity2enables the swarm to avert the dilemma,disperse,and form a trap pattern around the target.Thus,it is triggered in the proximity of the target.
(5) Obstacle:The boundary of obstacles is slightly inflated,and the shape of the inflated stuff is similar to the original one.Virtual agentsuvare infilled in the inflated region which supplies swarm buffering distance.These virtual agents only interact with robots only when robots truly observe them.The baseline vector vbaseindicated by virtual agents points perpendicularly to the polygon edge of the obstacle inward.The directionfrom the robotito the nearest virtual agentrnearis the initial desired collision-free vector between robots and obstacles at the current moment.The baseline vector vbaseindicated by virtual agents points perpendicularly to the polygon edge of the obstacle inward.Comparing the angle relationship between two vectors vobstacleand vbase,the plus-minus offset guiding robot to where possibly collision-free regions φ will be chosen.The avoiding process sustains until the robot leaves the designated regions in a radiusRavoidof any virtual agents.
(6) Final equation of sum velocity
To calculate the sum velocity,we take the vectorial sum of all the interaction terms introduced before
4.Experiment
4.1.Evaluation for grouping performance
Here,we shall test the proposed model and two rapid selforganized grouping methods that also group just with local information,i.e.,greedy grouping,chain-like grouping,adaptive decision-making grouping.(Figs.4(a)-4(c)).The greedy grouping,based on the closest distance,adds robots within the communication range to the swarm until the recruiting amount satisfies the predetermined value.This grouping method is widely used in leader-follower multiagent systems,such as Ref.[30],because the grouping topology is similar to the control topology.The chain-like grouping[34],inspired by the K-neighbor method,is that only one nearest member from a group is added to the swarm through an organizer,following which the member becomes the new organizer until the recruiting amount is satisfied.This grouping method significantly reduces communication load,compared with greedy grouping.Adaptive decision-making grouping [31]empowers grouping rights to individuals of the swarm,and these individuals decides on their grouping status according to their own observations toward targets.The grouping performance is directly calculated to measure the average maximum number of individuals a grouping method can muster.
4.2.Evaluation for multitarget trapping performance
Multitarget trapping performance is to evaluate global multitarget trapping performance by calculating the multiplicatively multiplication of actual number of robots to entrap different targets in multitarget environment with Eq.(16).Besides,the evaluation should be commonly used regardless of whether a swarm trapping method is centralized or decentralized.Thus,the formula of multitarget trapping performance(MTP) is
where the multitarget trapping performance is to multiplicatively multiply the non-zero actual number of trapping individuals around every target within the expected radius of trappingRtrap.When number of swarm robots is fixed,the maximum value of MTP calculated by fundamental inequality isNrobot/Nkwhen anyNkagnare equal.The greater MTP is,the better multitarget trapping performance is.
Encirclement occupancy,an evaluation index for target trapping problem proposed in Ref.[31],is to measure the quality of trapping in space.The distribution of robots within a certain trapping rangeRtrapin a certain number of directions around a target serving as an indicator of how uniformly the agents are positioned.Here,six directions are set to stay in step with the study [31].If there are robots staying at six directions within the trapping rangeRtrapat the same time and maintaining more than 2 steps,i.e.,encirclement occupancy remains equal to 1 more than 2 steps,reaching saturation entrapment is defined as this situation.
4.3.Experiment setting and scenario
In the first scenario(shown in Fig.5),the grouping test scenario was created to test the grouping performance of different grouping methods.Sixty robots were randomly generated on a 2 m × 2 m region,and a target was set to move and encounter the swarm at the left side of the swarm.The target would stop a while when the first robot observed it,and then kept going to the midpoint of the region.Besides,the positions of these robots in the 2 m×2 m scene were scaled up to a 4 m×4 m region to test grouping performance with different density of robots.In these two scenarios,different communication ranges were deployed with interval 0.5 from 0.5 to 2.0.

Fig.5.Grouping test scenario.
In the second scenario,we tested SUNDER-GRN in a complex confined multitarget scenario in a 25 m × 25 m region with ten targets including two dynamic targets and eight stationary targets,two hundred mobile robots,and night stationary obstacles,compared with H-GRN,EH-GRN,and AGENT.The experiment parameter setting is shown in Table 1.
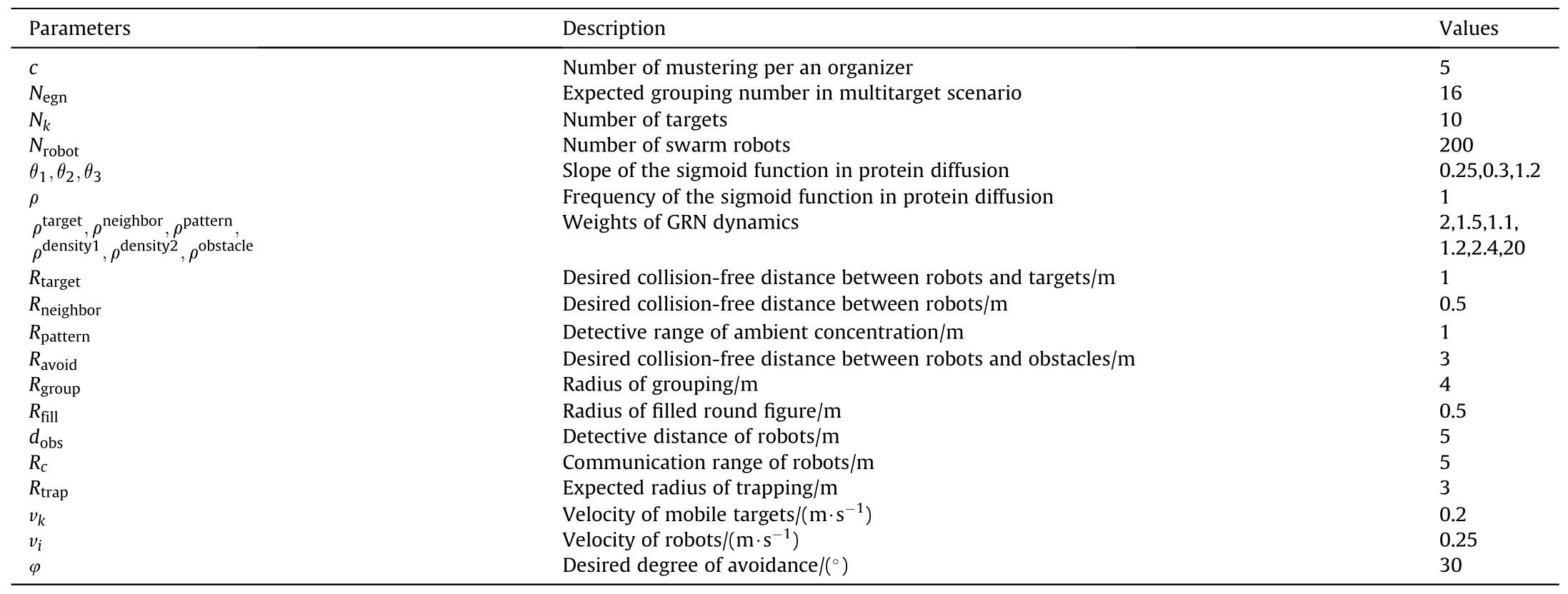
Table 1Notations used in simulations in a complex scenario.
5.Results and discussion
5.1.Grouping performance analysis
The experiments below were independently performed 20 times in the same 20 randomly generated swarm scenarios.Two experiments on subsections 5.1.1 and 5.1.2 are to test the performance of HSG in different parameter setting in scenario 1.Two experiments on subsection 5.1.3 are to verify the superiority of HSG compared with other grouping methods in scenario 1 and 2.
5.1.1.Number of mustering per organizer
The number of mustering per organizer was significant to HSG in the grouping process.Commonly,increasing the maximum number of mustering per organizer could enhance grouping performance so that more ungrouped individuals have chance to be mustered in subswarms.Correspondingly,an overmuch number of mustering easily led to a high communication load and then caused an inevitable delay.Hence,an appropriate value of the maximum number of mustering per organizer was beneficial to the performance of HSG.An experiment was held to measure the most appropriate number of mustering per organizerc,one of most important parameters in algorithm 1.We tested the number of mustering per organizer of HSG (20 randomized parallel experiments) in the first scenario,with three expected numbers of grouping on a scale of 60 agents(8,16 and 24)(shown in Fig.6).The result demonstrated excessive low value in the number of mustering per organizer restricted the grouping performance of HSG,especially on the condition with higher expected grouping number.The performance of grouping started to converge when the number of mustering per organizer exceeded 3 and reached a peak value of 5 achieving saturation grouping that all ungrouped individuals were grouped by a grouping method.

Fig.6.Number of individuals in the subswarm grouped by HSG from 60 robots.
5.1.2.Grouping and communication radius
Given the possibly infinite agents’grouping and communication radius,the grouping radiusRgroupwas further considered to estimate the influence on actual grouping.This experiment was held to explore the relationship between grouping radius and communication radius,because communication range could be unlimited,and thus it was possible for an organizer to choose an individual that possessed most neighbors but was far away from the organizer.It was easier to cause an unacceptable dispersive grouping pattern.In this experiment,the expected grouping numberNegnwas set at 8,16 and 24 respectively.The communication radius was set at 0.5 m,1 m,1.5 m,and 2 m respectively.The grouping radius was set at 0.2 m,0.4 m,0.6 m,0.8 m,1 m,1.2 m,1.4 m,1.6 m,1.8 m,and 2.0 m,respectively.The experiments were still executed within 20 randomized swarms in scenario 1.Fig.7 showed the result that the grouping radius greater than 1 m was able to satisfy perfect grouping at communication range from 0.5 to 2 m.When the grouping radius was greater than 1 m,HSG was able to maintain perfect grouping under the circumstance that the expected grouping was 8,16 and 24.There was another caveat about bad grouping pattern compactness that the greater grouping radius could cause more splitting subswarm because the process of choosing the organizer in HSG,merely considered the status of neighbors instead of the distance factor.The greater grouping radius might cause scattering grouping distribution,which easily restrained the activities for subswarm after grouping.Therefore,a suitable grouping radius to take place of the communication range in HSG could be chosen for improving grouping performance when grouping performance performed not well.
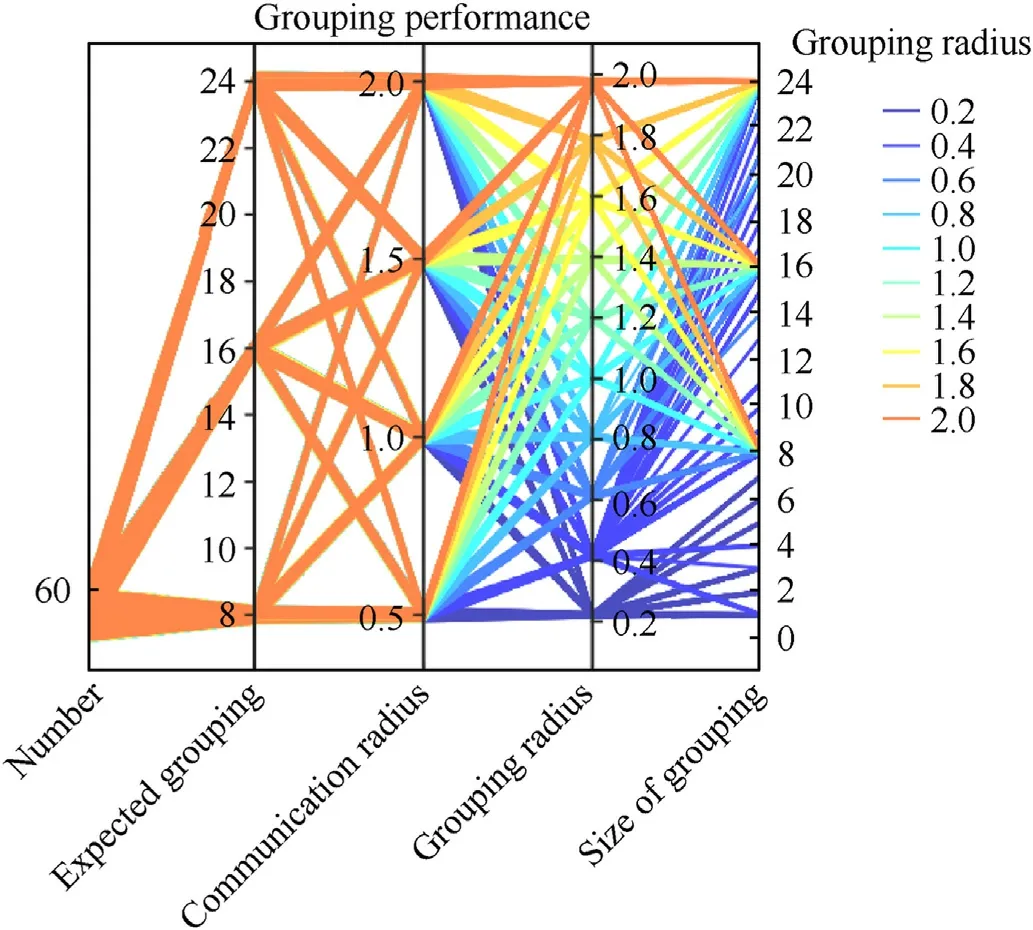
Fig.7.Grouping performance with different grouping ranges.
5.1.3.Comparative grouping performance analysis
For evaluating and analyzing the difference between HSG and comparative grouping methods,the experiments were also independently performed 20 times in the different 20 randomly generated swarm scenarios(shown in Fig.5).The average grouping performance was calculated to measure the average maximum number of individuals a grouping method can muster.The average grouping performance was corresponding to the number of partners a grouping method mustered.In the experiment,all grouping algorithms were required to make swarm robots muster partners on a 2 m × 2 m region as much as possible,that is,the more partners a grouping algorithm mustered,the better average grouping performance performed.Four different communication ranges were deployed with interval 0.5 from 0.5 to 2.0.
The result(shown in Fig.8)showed HSG performed better than other grouping algorithms in the experiment,which revealed outstanding grouping capacity when the communication range was small.In local information-based environment,communication resource was usually finite,it is verified that leveraging the number of neighbor of neighbors to achieve distributed grouping in HSG could muster more partners under such a condition.Greedy grouping method and ADM were easier influenced by small communication range,and chain grouping method perform ranked only second to HSG.In addition,HSG performed smaller fluctuations on grouping performance and mustered more than half of the swarm,while chain grouping method performed huge fluctuations when communication range is just 0.5 m.When communication range came to 2.0 m,only HSG achieve saturation grouping that a grouping algorithm musters all potential individuals.

Fig.8.Average grouping performance between comparative experiments on 2 m × 2 m region.
In the extended experiment,the test scenario was expanded to a 4 m×4 m region,and the density between robots became greater,which meant a robot possibly had fewer neighbors within a certain communication range.No surprisingly,the result(shown in Fig.9)showed all grouping methods cannot perform well in small communication range (CR =0.5 m),HSG and chain grouping method slightly performed better than greedy grouping method and ADM.When communication range came to 1.0 m,HSG performed better,but just half of swarm were grouped.When communication range came to 1.5 m and 2.0 m,the average grouping performance of HSG and chain grouping method was nearly equal.ADM had smaller fluctuations in these four grouping methods,and greed grouping method performed worst.
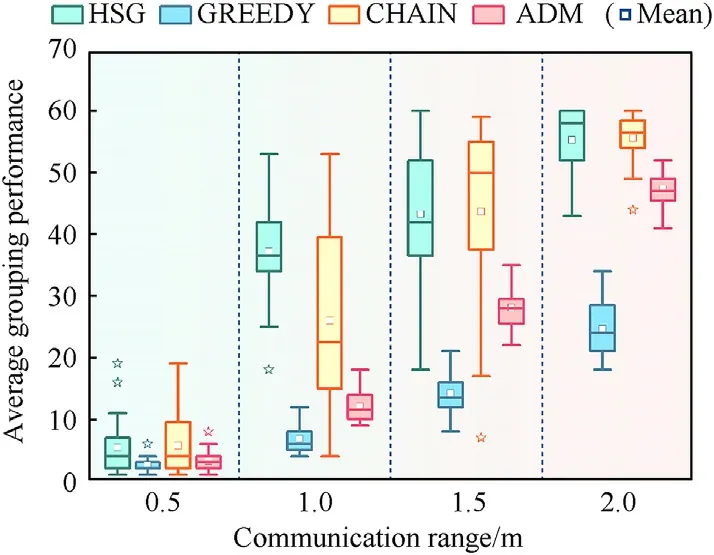
Fig.9.Average grouping performance between comparative experiments on 4 m × 4 m region.
In general,greedy grouping method,chain grouping method,and ADM performed worse than HSG because they were based on distance to muster partners.This kind of strategy was easier to cause a short-sighted effect.Greedy grouping method just mustered one robot ‘s neighbors that can be communicated to at one time,chain grouping method just considered the nearest neighbor to group while neglecting sustainable grouping,and ADM just empowered robots to group by themselves when the robots observed a target.HSG considered the maximum number of neighbor's neighbors to proceed with distributed grouping,which ensured sustainable grouping resource were maximum utilized,and thus HSG performed better than the distance-based grouping method mentioned above.
5.2.Complex scenario testing
To test the multitarget trapping performance of SUNDER-GRN,we simulated a 25 m × 25 m confined environment with ten targets and sudoku-shaped stationary obstacles.Two mobile targets were allowed to move freely,and the others were kept stationary.The main target,which was closest to the swarm,navigated in the northeast direction and escaped from the swarm until reaching the top right-hand corner.Another mobile target navigated in the southwest direction and followed a reciprocal motion.Mobile targets possessed the unequal condition,i.e.,they could pass through the inside of obstacles (as a type of single advantage),while the swarm robots could only bypass the obstacles.Two hundred robots,generated on the base(5 m×5 m on the bottom left-hand corner)and randomly numbered from 1 to 200,tried to entrap all targets in the environment.The swarm needed to entrap every target they newly discover during the journey of trapping the main target.The results of multi-target trapping experiments were presented in Fig.10.In addition,three ablation studies in Fig.11 are carried out to justifying the correctness of our proposed algorithm.We analyzed the differences and causes to verify the superiority of our proposed method over the three compared algorithms(H-GRN,EH-GRN,and AGENT) in Fig.12.The Moreover,the quantitative analysis of multitarget trapping performance was depicted in Figs.13-15.
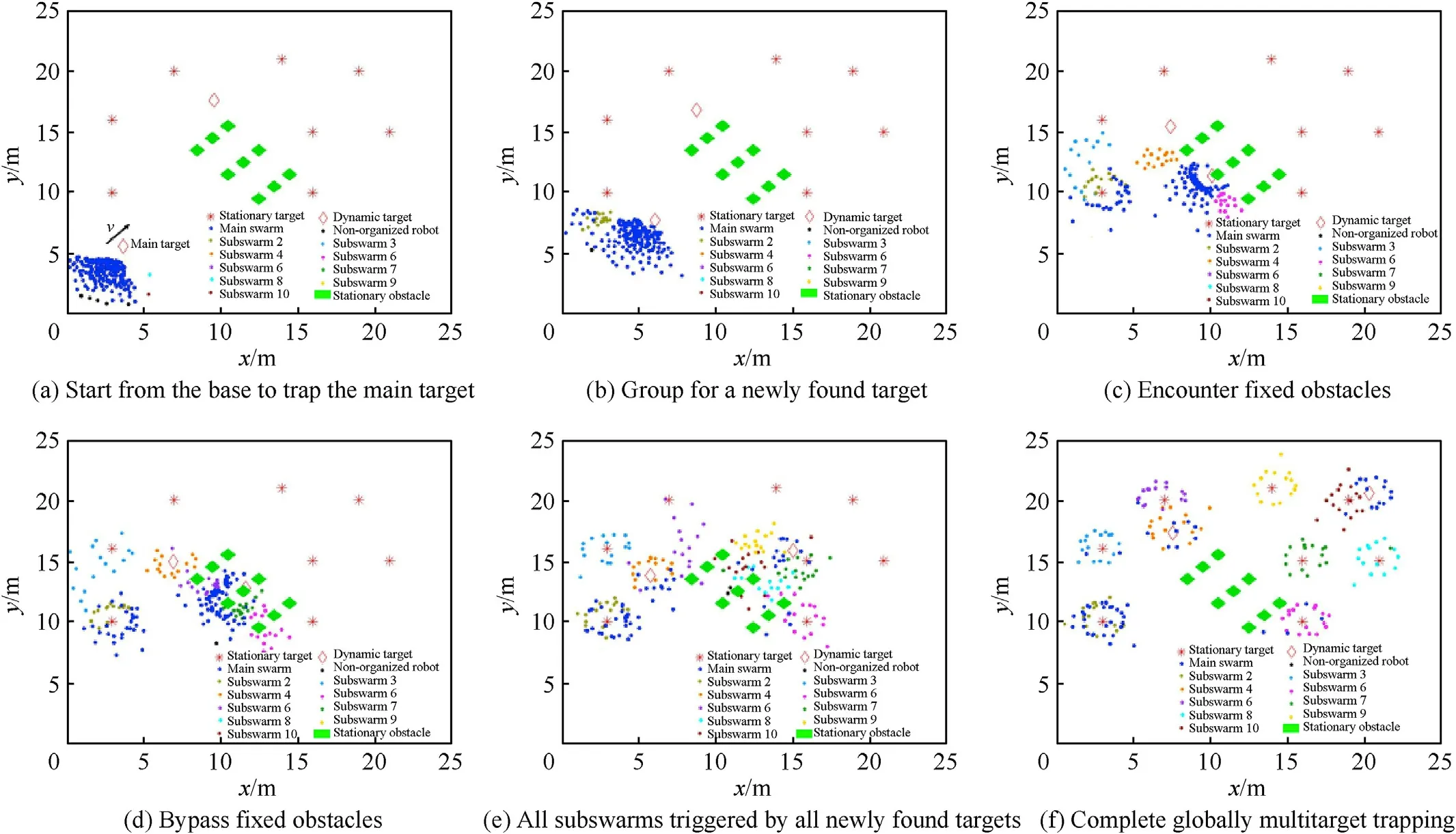
Fig.10.SUNDER-GRN Process of entrapping 10 targets with 200 robots in the confined and local information-based environment: (a) Initially,the swarm starts from the base to entrap the mobile main target;(b) The main swarm group and sunder for a newly found target after observing it;(c) The main swarm encounters stationary obstacles while grouping and sundering for another three targets;(d)The main swarm bypasses the stationary obstacle;(e)The main swarm keeps away from stationary obstacles and groups for the remaining targets;(f) All targets in this confined environment are trapped by subswarms.
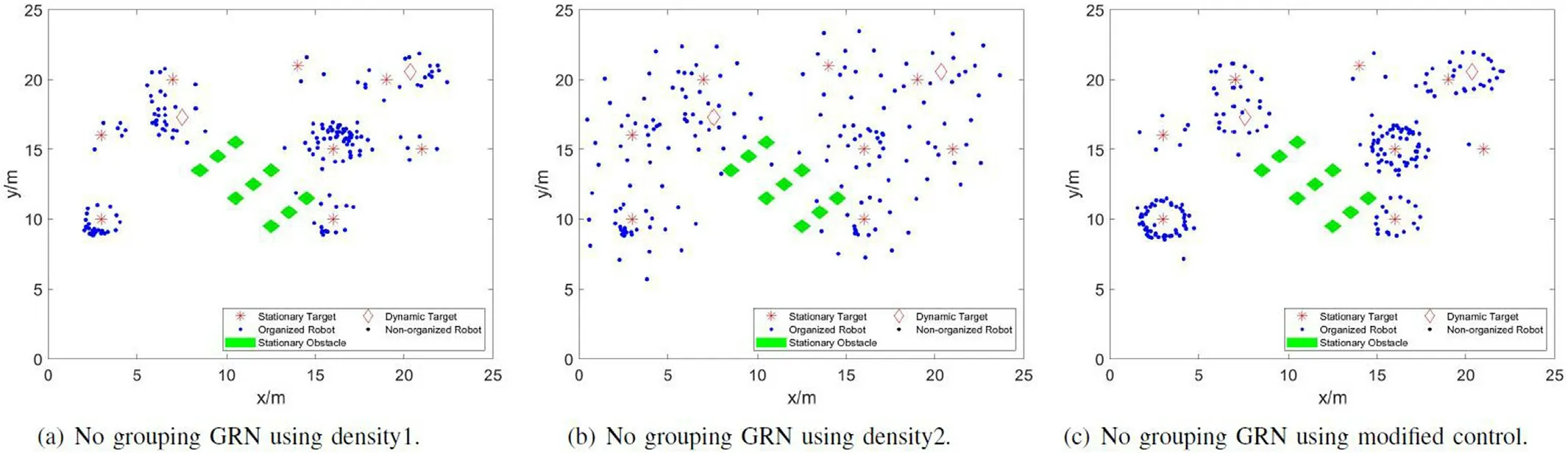
Fig.11.Example of the ablation studies of Sunder-GRN: (a)No grouping GRN using density 1;(b) No grouping GRN using density 2;(c) No grouping GRN using modified control.
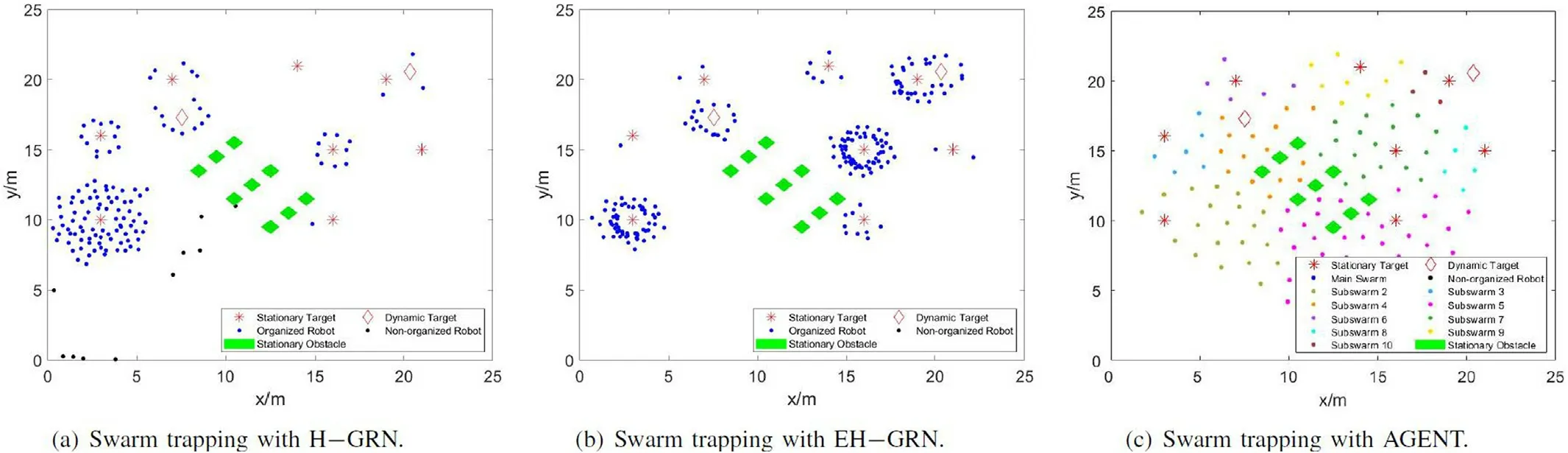
Fig.12.Performance of comparative algorithms in multitarget trapping scenario: (a) H-GRN;(b) EH-GRN;(c) AGENT.
Fig.10 illustrates the different stages of a typical run of the SUNDER-GRN experiment in the complex scenario.Initially,the isomorphic swarm deployed in the base(2 m×2 m on the bottom left-hand corner) tried to entrap the main dynamic target,which was going to escape towards the northeast direction at a rate of 0.5/m (shown in Fig.10(a)).The swarm started to sunder and form subswarm 1 in terms of HSG when the swarm encountered the first newly found stationary target.Meanwhile,some agents followed subswarm 1 because of the cohesive characteristics of swarm collective movement (shown in Fig.10(b)).The main swarm avoided obstacles and followed the main target closely,and subswarm 6 grouped for another newly found target(shown in Fig.10(c)).Then,the main target got through the sudoku-shaped stationary obstacles which the swarm had to bypass,and the other three newly found targets were detected to form subswarms 3-5.Subswarm 4 and 5 departed from the main swarm to entrap a dynamic target and another stationary one,respectively.Subswarm 3 sundered from those ungrouped individuals following subswarm 2(shown in Fig.10(d)).Next,the grouping process happened constantly,and subswarm 6-10 succeeded in grouping triggered by the remaining targets after the main target left the sudoku-shaped obstacle region(shown in Fig.10(e)).Finally,the two dynamic targets stopped and the subswarms’ trapping pattern for the corresponding targets tended to become stable (shown in Fig.10(f)).There are some ungrouped organized robots that are scattered around the targets and attending to trapping.The residual main swarm and subswarm 10 collectively trapped the main target and the tenth-discover target,which took advantage of the distributed characteristic of local GRN.
To demonstrate the authenticity of the modules of SUNDERGRN,three ablation studies are carried out.The first study(shown in Fig.11(a)) cuts out the grouping method (HSG) and the modified GRN.The original GRN with relative coordinate system is used to control swarm to form multi-target trapping pattern.The density item is set at 1.2.The result shows some trapping swarm robots was badly affected by the process of updating relative coordinates,which leads to uneven trapping character that some swarm robots aggregate excessively at one side of a target.Worse still,the targets are not correctly trapped,and they can easily escape from the incomplete trapping pattern.The second study(shown in Fig.11(b))is the same as the first one except the density value which is set to 2.4.The loose trapping pattern is exhibited,and the uneven spatially distributed problem still exists.The study verifies the simple adjustment of density value cannot solve trapping pattern problem.The third study (shown in Fig.11(c)) substitutes the modified GRN for the original GRN.The swarm robots can form complete trapping patterns around targets.There are three targets not entrapped that has long distance to the main target because the concentration abyss (shown in Fig.2) obstructs swarm robots.This study verifies the usefulness of modified GRN that improves trapping pattern formation,and the grouping method (HSG) is needed to further promote multi-target trapping performance.
Comparative algorithms (H-GRN,EH-GRN,and AGENT) are deployed in the same complex scenario (shown in Fig.12).The results reflect a respective deficiency in the multitarget trapping scenario.As for H-GRN,the controller of the swarm is vulnerable to concentration standing for predictive trapping pattern,thus,the superabundant individuals tend to trap the nearest target and some of them get lost and switch to non-organized status.The congestion occurs because the trapping process obstructs those individuals at the edge.At last,there are five targets not well trapped by the swarm for H-GRN (shown in Fig.12(a)).As for EH-GRN,more adequate trapping performance can be witnessed,but those targets far away from the main route that the main target went by cannot be trapped well because the concentration abyss between two targets restrains the swarm to have a further try though they had observed them;that is,the swarm has inertia to access the target that is closer(shown in Fig.12(b)).As for AGENT,adaptive decisionmaking strategy (ADM) prompts swarm robots dynamically group according to the local environment,but the controller based on potential field cannot guide the large-scale robots to entrap which target the grouping hints (shown in Fig.12(c)).The result can be understood because of the separation between ADM and potential field control scheme which does not receive the feedback from grouping result (shown in Figs.1-12(c)).Contrarily,the grouping result in SUNDER-GRN relates to the trapping pattern formation for subswarm,thus take a rapid response for subswarms to entrap targets which the grouping results hint.
Finally,the multitarget trapping performance in the complex scenario between SUNDER-GRN,H-GRN,EH-GRN,and AGENT are exhibited in Fig.13.To ensure the fairness of comparison,the initial positions of the swarm are randomly generated and synchronized in the four trapping methods within ten parallel experiments.Besides,the shadow reflects the data fluctuation in 10 parallel experiments.The actual numbers of agents around the 10 targets within 3 m are regarded as the effective trapping number.The result of multitarget trapping performance (MTP) shows that SUNDER-GRN has better multitarget trapping performance that other algorithms.The GRN without grouping and EH-GRN are ranked second and third,respectively.H-GRN and AGENT perform badly in the large-scale swarm scenario.As swarm robots encounter more and more targets,the MTP values of SUNDER-GRN,GRN without grouping and EH-GRN start to rise.When the number of iterations reaches 105,GRN without grouping and EH-GRN level off because they cannot entrap few long-distance targets well.SUNDER-GRN leverages combining grouping and modified control scheme to entrap those few long-distance targets well,and thus the MTP values keep rising.
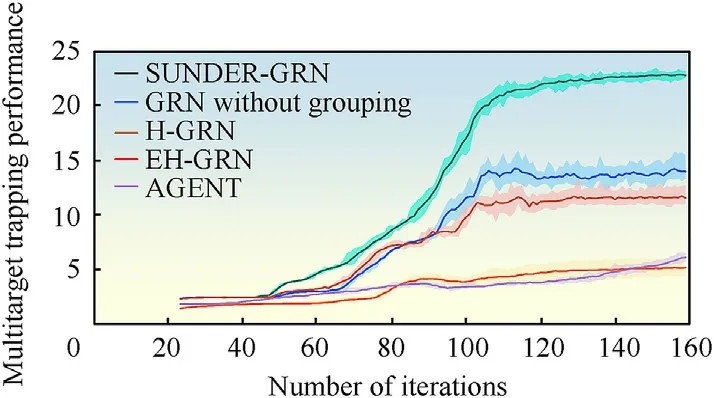
Fig.13.Comparative results in multitarget trapping performance between Sunder-GRN,GRN without Grouping,H-GRN,EH-GRN,and AGENT.
Encirclement occupancy,an evaluation index for target trapping problem proposed in Ref.[31],is to measure the quality of trapping in space.The distribution of robots within a certain trapping rangeRtrapin a certain number of directions around a target serving as an indicator of how uniformly the agents are positioned.Here,six directions are set to stay in step with the study [31].If there are robots staying at six directions within the trapping rangeRtrapat the same time and maintaining more than 2 steps,i.e.,encirclement occupancy remains equal to 1 more than 2 steps,reaching saturation entrapment is defined as this situation.The start time of saturation entrapment is calculated to measure the start time of forming a stable entrapment for targets with a trapping method.The result (shown in Fig.14) demonstrates our proposed method SUNDER-GRN succeeds in covering all targets and forms stable entrapment for all targets faster than other trapping methods.The result also explicitly reveals the number of targets achieving the saturation entrapment.H-GRN and AGENT both achieve the saturation entrapment for 4 targets,and EH-GRN achieves the saturation entrapment for 5 targets.Driven by the grouping method HSG in SUNDER-GRN,the swarm triggered by targets sunders fast to sub-swarms and thus reduce response time for targets,which demonstrates the superiority of SUNDER-GRN in multitarget trapping scenario.

Fig.14.Start time of saturation entrapment between Sunder-GRN,GRN without Grouping,H-GRN,EH-GRN,and AGENT.
In addition,no trapping methods can ensure the maintenance of saturation entrapment for targets in a changing environment all the time,thus duration of saturation entrapment which exhibits the stability of saturation entrapment can further evaluate a trapping method.The result (shown in Fig.15) shows HSG outperform comparative trapping methods in the stability of saturation entrapment.Other comparative grouping methods cannot achieve lasting saturation entrapment for most of the targets well,except for target 7,because target 7 is stationary and closer to the main target in complex scenario,thus more individuals are attracted to entrap the target 7.
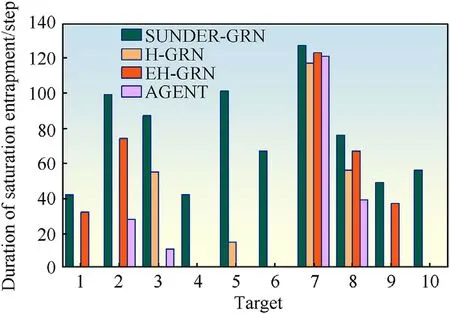
Fig.15.Duration of saturation entrapment between Sunder-GRN,GRN without Grouping,H-GRN,EH-GRN,and AGENT.
6.Conclusions
A regulatory network with a Self-organized grouping and entrapping method for swarms (SUNDER-GRN) was proposed,which empowers a swarm to rapidly structure subswarms based on the HSG algorithm and to drive them to entrap targets without the aid of global information.Two experiments were performed to validate appropriate settings of parameters in HSG algorithm,and another two comparative experiments were performed to verify that HSG algorithm has superior grouping capacity than greedy grouping,chain grouping and ADM.Moreover,SUNDER-GRN was tested in a large-scale confined scenario with 10 targets and 200 swarm robots.Ten independent experiments were conducted to show that SUNDER-GRN outperformed other methods in comparison,including the quantity of robots entrapping different targets,the efficiency of entrapping different targets,and the quality of trapping formation.
SUNDER-GRN has great potential to be deployed to real robot platforms.Future works would include testing in more complex 3-D environments,extending the proposed method to real UAV swarms in outdoor GPS-denied environments,and designing more effective indicators on swarm grouping.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This research was supported in part by National Key R&D Program of China (Grant Nos.2021ZD0111501,2021ZD0111502),the Key Laboratory of Digital Signal and Image Processing of Guangdong Province,the Key Laboratory of Intelligent Manufacturing Technology (Shantou University),Ministry of Education,the Science and Technology Planning Project of Guangdong Province of China (Grant No.180917144960530),the Project of Educational Commission of Guangdong Province of China (Grant No.2017KZDXM032),the State Key Lab of Digital Manufacturing Equipment &Technology (grant number DMETKF2019020),National Natural Science Foundation of China(Grant Nos.62176147,62002369),STU Scientific Research Foundation for Talents (Grant No.NTF21001),Science and Technology Planning Project of Guangdong Province of China (Grant Nos.2019A050520001,2021A0505030072,2022A1515110660),Science and Technology Special Funds Project of Guangdong Province of China (Grant Nos.STKJ2021176,STKJ2021019),and Guangdong Special Support Program for Outstanding Talents(Grant No.2021JC06X549).We would like to thank Editage (www.editage.cn) for English language editing.
- Defence Technology的其它文章
- Deep learning-based method for detecting anomalies in electromagnetic environment situation
- Impact point prediction guidance of ballistic missile in high maneuver penetration condition
- Real-time localization for underwater equipment using an extremely low frequency electric field
- Numerical simulation of flow field characteristics and theimprovement of pressure oscillation of rotating detonation engine
- Comparative investigations of ternary thermite Al/Fe2O3/CuO and Al/Fe2O3/Bi2O3 from pyrolytic,kinetics and combustion behaviors
- Adaptive saturated tracking control for solid launch vehicles in ascending based on differential inclusion stabilization

