Combustion crack-network reaction evolution model for highlyconfined explosives
Zhuo-ping Duan,Meng-Jing Bai,Zhi-ling Bai ,Xin-jie Wang,Feng-lei Huang
State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China
Keywords:Solid explosives Non-shock ignition Self-enhanced combustion Combustion crack-network (CCN) model Relief area Reaction degree
ABSTRACT The evolution behavior of combustion crack reaction of highly confined solid explosives after non-shock ignition is governed by multiple dynamic processes,including intrinsic combustion of explosives,crack propagation,and rapid growth of combustion surface area.Here,the pressure increase can accelerate the combustion rate of explosives,and the crack propagation can enlarge the combustion surface area.The coupling between these two effects leads to the self-enhanced combustion of explosive charge system,which is the key mechanism for the reaction development after ignition.In this study,combustion cracknetwork (CCN) model is established to describe the evolution of combustion crack reaction of highly confined solid explosives after non-shock ignition and quantify the reaction violence.The feasibility of the model is verified by comparing the computational and experimental results.The results reveal that an increase in charge structure size causes an increase in the time of crack pressurization and extension of cracks due to the high temperature-generated gas flow and surface combustion during the initial stage of explosive reaction,but when the casing is fractured,the larger the charge structure,the more violent the late reaction and the larger the charge reaction degree.The input pressure has no obvious influence on the final reaction violence.Further,a larger venting hole area leads to better pressure relief effect,which causes slower pressure growth inside casing.Larger reserved ullage volume causes longer lowpressure induction stage,which further restrains the internal pressure growth.Furthermore,the stronger the casing constraint,the more rapid the self-enhanced combustion of the high temperaturegenerated gas,which results in more violent charge reaction and larger charge reaction degree during casing break.Overall,the proposed model can clarify the effects of intrinsic combustion rate of explosives,charge structure size,input pressure,relief area,ullage volume,and constraint strength on the reaction evolution,which can provide theoretical basis for violence evaluation and safety design for ammunition under accident stimulus.
1.Introduction
During the storage,transportation,and handling of conventional ammunition,accidental thermal/mechanical stimuli,including impact,shock,burning,or long-term exposure in hightemperature environment cannot be avoided.The non-shock ignition can trigger deflagration or even detonation,which can lead to catastrophic consequences.The non-shock ignition reaction evolution of typical ammunition charge is very complex and is influenced by several factors,including constrained strength,inertial constraint ability,intrinsic combustion features of explosives,and crack propagation.This process involves the dynamic damage in explosive,the initiation,development,and furcation of cracks as well as the gas-solid coupling and liquid-solid coupling between cracks and gas products,which represents typical multi-physics,multifactor,and multi-process associated reaction behavior.Obtaining a clear understanding of the evolution of non-shock ignition accidental reaction of ammunition charge has always been the bottleneck for the safety study of explosives,which restricts the development of safe ammunition and evaluation [1,2].
The present works on the evolution of non-shock ignition of explosive charge are still in an early stage with primary focus on experimental research.For example,the reaction evolution process of highly-confined PBX9501 explosive with one-dimensional (1D)preset cracks has been experimentally investigated [3-6].It has been found that the higher the length-width ratio of cracks,the more violent the combustion reaction.A sudden change in the combustion rate is considered as an indicator of convective combustion.Further,several researchers have investigated the evolution of ignition reaction of constrained annular,cylindrical,and spherical PBX9501 explosive charge [7-14].The spontaneous/forced ignition in the central zone of explosive generates hot gas products,which enter the bulk cracks and the ullage between explosive and casing.These gas products heat the explosive near the cracks and cause surface combustion at the crack surfaces.This leads to rapid pressure build-up,rapid propagation and furcation of cracks,formation of the crack network,and increase in the combustion surface area.This process is called self-enhanced combustion (convective combustion).In addition,the pressure builds up rapidly till the fracture of casing.Hu et al.[15]examined the evolution of the crack network reaction in the DDT tube experiment of highly confined typical HMX-based pressed PBX.Based on several laboratory-based experimental results,there exists an initial consensus on the dominant mechanism of the evolution of typical solid explosive ignition reaction[16,17].After the ignition of highly confined explosive,the reaction growth is governed by several dynamic processes,including the intrinsic (degradation) combustion of explosive,crack propagation,and rapid growth of combustion surface area.Further,the increase in the pressure promotes the intrinsic combustion rate of explosives,and the crack propagation causes an increase in the combustion surface area.The synergistic effect of the two leads to the self-enhanced combustion of explosive charge.This is the main mechanism for the reaction growth after ignition.
Solving the gas/liquid/solid coupling issue of crack propagation driven by high-temperature gas product combustion is a major challenge in establishing a numerical model for the initiation,propagation,and coalescence of dynamic cracks.The time scale of actual non-shock ignition and reaction evolution far exceeds the ability of numerical modeling.Therefore,the numerical study on the evolution of combustion crack reaction is still in a qualitative stage,and only few works have been reported.
Further,with regard to theoretical modeling,there is no systematic and satisfactory model that can be used to effectively describe and predict the evolution of combustion crack reactions of explosives.Therefore,the theoretical modeling of non-shock ignition reaction evolution of constrained explosives is far from mature.A pressure-enhancement model of 1D combustion crack has been established based on pressure evolution of highly confined explosive with single crack combustion[18-20].Hill et al.[21]proposed a combustion network model for a constrained explosive by considering the distribution rule of internal voids of explosive charge and primarily realized the modeling of explosive charge reaction evolution.However,a comparison with the experimental results was not provided,so the effectiveness of the model still needs to be verified.Additionally,only single influencing factor was considered in the model,which was significantly different from the practical engineering situation.
In this study,for the conventional brittle PBX explosive,an evolution model of combustion crack-network reaction is established by considering the factors,including casing constraint,pressure relief structure,and ullage volume.In addition,the model is used to predict the reaction evolution after the ignition of constrained explosive charge and to quantitatively characterize the reaction violence of the system.The feasibility and efficacy of the model is validated by comparing the modeling results with the experimental results.Overall,the proposed model can serve as a useful theoretical basis for safety design and numerical evaluation of ammunition.
2.Establishment and verification of combustion cracknetwork (CCN) model of highly confined explosives
Fig.1 illustrates the established combustion crack-network(CCN) model of constrained explosives.Ignition occurs at the central position of the charge with certain degree.Further,a local crack is generated,and burning is extended within the cracks.The sound velocity of explosive is of the same magnitude as that of the crack propagation driven by combustion,and it is assumed that the local pressure perturbation is instantaneously distributed in the entire explosive system.It is constrained by an inert casing with spherical,cylindrical,or other regular shapes to reach dynamic equilibrium.It is noteworthy that the cracks mentioned in this study refer to the macro-and meso-scale voids,cracks,and other damage caused by various stimuli in the solid explosive charge.
The total volume of explosive system(V)includes the explosive volume(Ve) and crack volume (Vc)
The cracks are treated as thin walls,i.e.,
whereSand δ are the total surface area and width of crack network.
Att=0,the internal pressure of casingP0is equal to 0.Assuming no cracks exist in the explosive,the volume of explosive system is expressed as follows:
At the starting point of ignition,the internal pressure of casing reachesP0and the explosive bulk is partially fragmented,resulting in randomly distributed cracks.In this case,the crack width is δIG.In the following stage of combustion,the pressure is raised.Using Eq.(1) -Eq.(3),we get
The relative volume change of internal space of casing is the volumetric strain of the entire explosive system,(V-V0)/V0=εv.It is assumed thatP=Iεv,whereIis the generalized equivalent stiffness of casing.The casing material is described by ideal elastoplastic model.For casing with different shapes,including annulus,cylindrical,and spherical,the expression of generalized equivalent stiffnessIduring elastoplastic deformation is given in appendix A and B.In addition,the volumetric strain of explosive is (Ve-Ve0)/Ve0=εve,so we can getVe/Ve0=1+εvewhich is satisfied withP=-,whereBis the bulk modulus of explosive.
The generalized stiffness of the system is defined asM,which satisfies
After ignition,the high-temperature gas rapidly enters the cracks by thermal damage and ignites the explosive.The pressure increase within the cracks promotes the gas products to enter thinner cracks.Meanwhile,the rapidly generated gas products cannot flow out from the crack,leading to gas blockage.This further causes a dramatic pressure increase in the cracks,drives rapid crack furcation and propagation,and increases the combustion surface area to form the CCN.As the pressure increases,the combustion rate is further enhanced.The increase in the combustion surface area together with the enhancement of combustion rate promotes the drastic increase of pressure.
From the perspective of probability and statistics,Weibull distribution model is usually used to describe the existence of a large number of randomly distributed defects in materials,and the material failure is caused by the weakest chain,which is widely used in the characterization of microcrack propagation fracture failure of brittle materials.Considering that cracks propagate irregularly and randomly,the properties of CCN can be described by Weibull distribution to establish the relationship between the microstructure of CCN after ignition and the macroscopic properties.After ignition,the probability density functionf(P)for the propagation of a certain crack under pressurePcan be defined as follows:
wheremis the shape parameter,which is generally considered as a constant.Pcis a scale parameter,andP0is the input pressure.According to weakest link principle,the probability of crack network propagation due to explosive charge combustion under pressurePis
There are enough cracks in the explosive charge system,and the combustion crack bifurcates and propagates into networks.The number and area of cracks can be statistically treated.Hence,the surface areaSand pressurePof CCN are related as follows:
whereSmaxis the saturated specific surface area of combustion crack(cm2/g),which is related to the charge properties.When the charge is spontaneously ignited,the activated combustion surface areaSIG(cm2) is determined by the charge properties and initial temperature.When forced ignition occurs,SIGis also related to the input pressureP0,which can be calibrated by typical experiment.
Compared to the saturated state area of crack during the later period of combustion evolution,the initial combustion crack surface areaSIGactivated by local ignition is several magnitudes smaller.The scale parameterPcandmare the key physical quantities that reflect the influence of explosive charge properties on the evolution properties of CCN.To analyze the evolution properties of CCN,P0=1.0 MPa is used to calculate the variation rule of CCN surface area with pressure under different values ofPcandm.As shown in Fig.2,the smaller the value ofPcor the higher the value ofm,the faster the propagation of CCN of explosive charge.The growth of crack network surface area with pressure is a slow-fastslow process.The pressure gradient is low during the early stage of combustion and the crack propagation is slow,where the degradation combustion of explosive is dominant.The degradation combustion rate of explosive is raised with pressure,leading to acceleration of crack propagation driven by high-pressure gas products.In the late stage,the pressure keeps increasing,while the crack network reaches saturation due to casing constraint.

Fig.2.Variation in the surface area of CCN as a function of pressure.
Hence,the width δIGof crack at the beginning of combustion is
The combustion rate of explosives satisfies Vielle law [1],i.e.,
Hence,the increase rate of gas product mass is
It is assumed that the product is an ideal gas mixture,thus
Differentiating the above equation with respect to timet,and using Eq.(6),Eq.(7),Eq.(9),Eq.(11) and Eq.(12),we get
The relationship between pressurePand timetduring the nonshock ignition reaction of solid explosive charge is expressed as follows:
The structural strength is generally constrained by vulnerable linking parts.The internal pressure of several hundreds of MPa within a time scale of several hundreds of microseconds and even milliseconds is sufficient to cause the rupture of casing.Further,the pressure during the later period can be rapidly increased to GPa level under structural and inertial constraint,driving the fracture of casing.To simplify the calculation,the inertial effect is neglected and the fracture of casing is considered to be an instantaneous process(internal pressure reachesPbbefore rupture).The moment for casing break istb,and the reaction degree of explosive charge in this case (mass ratio of reacted explosives)is
The product of total amount of energy release efficiency and peak energy release rate efficiency is used to represent the reaction violence of the system[18],i.e.,
whereEis the total amount of energy released by the charge reaction(kJ/g),andis the peak value of time derivative of energy(power peak).Qfis the combustion heat,andis the peak value of charge reaction rate.are charge explosion heat and detonation power (n=1 indicates cylindrical charge,n=4 indicates spherical charge).The rationale behind this definition comes from the fact that a damaging explosive accident must have both high energy and high peak power.This in turn produces high pressure and impulse at a high rate.We usually choose the detonation state as the standard case for dimensionless processing,the total energy release is now simply characterized by the product of reaction degree and reaction heat,and the power is quantified by the product of peak reaction rate and reaction heat,and much work in depth will be done to perfect this function in the future study.
Typically,the position and fracture mechanism of casing under internal pressure is determined by its structure.For spherical/cylindrical projectile with thin wall,the casing is expanded circumferentially till break.For cylindrical projectile with medium/thick wall,the strength of end cap connection structure is weak and shear failure happens there,resulting in the breaking of end cap.In this study,we only focus on the ideal symmetric homogeneous deformation induced failure.The local failure mode will be considered in future work.
The process of casing deformation till fracture is complex.Therefore,an appropriate description of its properties,especially determining the fracture time of casing,is the key for accurately estimating the total reaction amount of explosive charge.In this study,the ideal elastoplastic constitutive model is used,and the maximum strain is considered as the criteria for failure(the failure strain is temporarily set as [ε]=5%) to describe the casing deformation until failure.For thin casing and medium-thick/thick casing,thin-wall model and medium-thick/thick-wall model are established to analyze the process of casing deformation till fracture.The expressions of generalized equivalent stiffness I and the response time of casing deformation till failure are shown in appendix A and appendix B.Herein,the expression of generalized equivalent stiffness I obtained by thin-wall model is concise and convenient,which can enhance the calculation efficiency within the error limits in practical engineering application.All numerical calculations are carried out using a home-made MATLAB program.
To verify the applicability of the thin-wall model,the reaction evolution of highly confined spherical PBX9501 explosives with steel structure after forced ignition is evaluated by using thin-wall model and medium-thick/thick-wall model.The thermodynamic parameters and casing parameters of PBX9501 explosive used in the calculation are shown in Table 1.The internal radius of spherical steel casingRi=5.5 cm.The calculation results of thin-wall model and medium-thick/thick-wall model are compared by changing the wall thickness (see Fig.3).As the casing thickness decreases,the differences between these two models in terms of the pressure change and reaction degree change during the ignition reaction evolution of explosive charge are both reduced.When the casing is extremely thin,the medium-thick/thick-wall model can be reduced to the thin-wall model,which verifies the validity of the thin-wall model.

Table 1Thermodynamic parameters and casing parameters of A1 explosive used in the calculation [13].
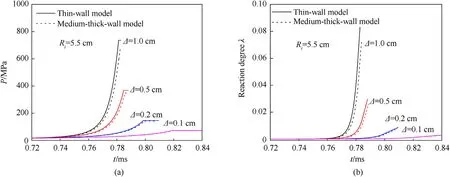
Fig.3.Comparison of calculated results by thin-wall model and medium-thick-wall model under different wall thickness: (a) Pressure-time history;(b) Reaction degree-time history.
The Hill model [21]and the proposed medium-thick-wall theoretical model are used to compute the reaction evolution after forced ignition of highly confined spherical PBX9501 explosives with steel structure under the same experimental conditions as in an earlier study [13].Here,the radiusRiof PBX9501 charge is 5.5 cm.The thermodynamic parameters of the explosive are shown in Table 1.The thickness of spherical steel casing is Δ =2 cm.It is worth noting that,there are reinforced base and sleeve outside the spherical casing in the earlier experimental setup [13],which further reinforces the structural strength of casing constraint.We simply increase its equivalent structural yield strength to 2000 MPa to adapt to the theoretical calculation of regular spherical casing deformation.As shown in Fig.4(a) [13],the calculation results based on this model are in good agreement with the experimental data,which verifies the validity of this model.The superiority of the proposed model over Hill model can be attributed to the following reason.Hill model simply uses the Belyaev criterion to characterize the initial surface area of crack-network under different pressures[18,22].Since the contribution of crack propagation is neglected,the computed combustion network surface area of charge reaction in the later stage is small,the reaction rate is low,and the pressure build-up is slow.The computational results based on the proposed theoretical model and the experimental results show that the pressure build-up history after explosive ignition exhibits typical three stages:induction stage,exponential growth stage,and highspeed linear growth stage.In the induction stage,the flame gas has long-range flow along the cracks in the explosive bulk to heat and ignite the explosive.The intrinsic degradation combustion rate is low and the crack propagation is slow,indicating stable growth properties under low pressure.Driven by higher pressure in the exponential growth stage,the coupling effect between the acceleration of the intrinsic degradation combustion rate and the rapid increase of the CCN surface area causes self-enhanced combustion with exponential growth properties.In the linear growth stage,the surface area of CCN is saturated without further enhancement.High pressure maintains high degradation combustion rate,which causes fast pressure growth with linear properties.
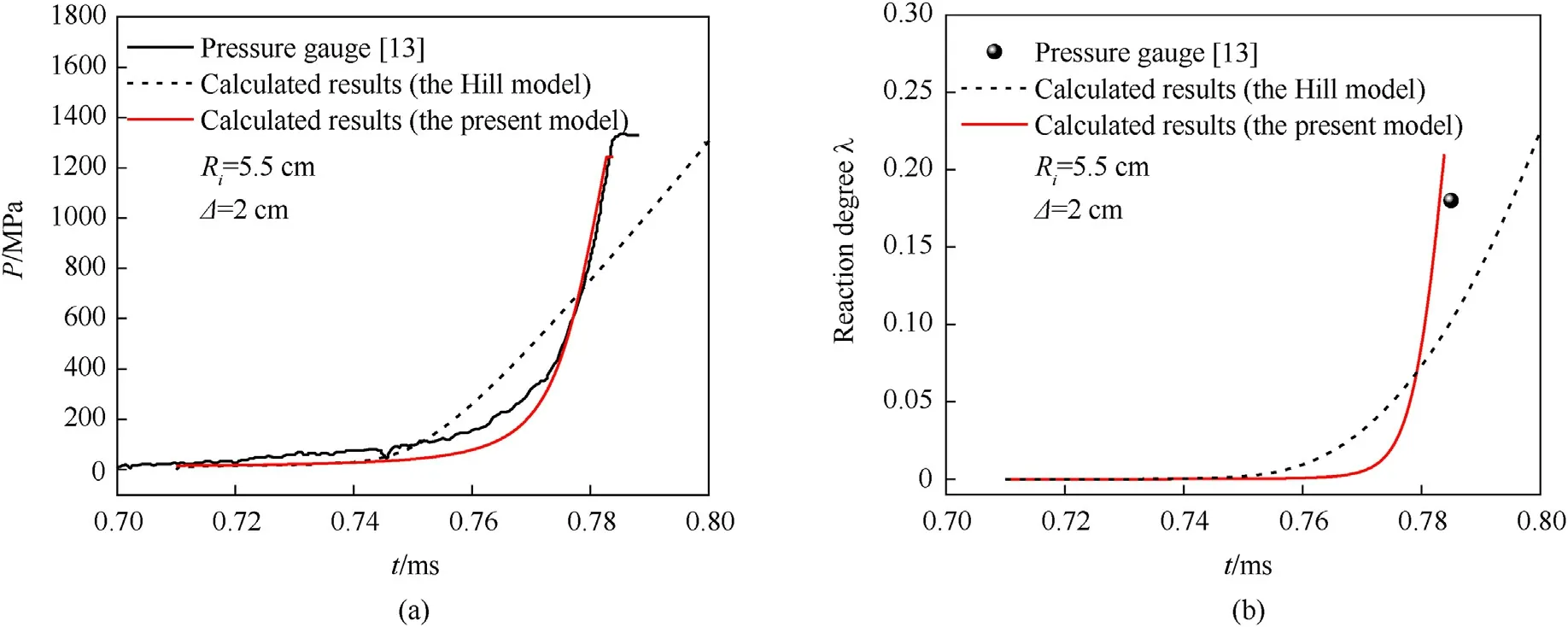
Fig.4.Comparison between the calculated results and experimental results of non-shock ignition reaction growth for highly confined (spherical constraints) explosives.
The reaction degree curves at period from ignition to casing fracture calculated by this model are shown in Fig.4(b).When the casing fractures,the reaction degree is 20.9%,and the reaction violence is 0.0234.Compared with the reaction degree of 18% estimated by the overpressure data in Ref.[13],the validity of this model is primarily verified.Additionally,it is necessary to note that the calculated pressure when the casing fractures is lower than the experimental value because the proposed model uses ideal elastoplastic constitutive model and maximum strain as the criteria for failure without considering hardening of casing material and inertial effect of casing constraint.The casing deformation will be further optimized in future works.
It is important to note that the proposed model can reflect the influence of casing material strength,including elastic modulus,yield stress,and strength on the evolution of reaction.However,this study only focuses on the structural design of casing without examining the effect of casing material,which will be discussed in future work.
In the calculation,steel spherical structures are used,and the influence of casing size (charge size) and casing thickness on the reaction growth after ignition is analyzed.As shown in Fig.5,under the condition of geometric similarity (radius ratioK=R0/Ri=1.3636),larger charge diameter leads to longer time for pressurization and extension of cracks due to the high-temperature gas flow and subsequent surface combustion in the early stage after explosive ignition.The combustion reaction of explosive is slower in the early stage,the pressure growth is slower,and the response time for casing deformation is longer.However,the internal pressure when the casing is finally fractured,the total amount of explosive charge reaction degree,and the total energy released by charge are the same.The final reaction violence is large for the charge with larger diameter.The reason is that,as the reaction goes on,the growth rate of combustion reaction surface area is rapid at the later stage of reaction evolution for the large charge size,resulting in fast reaction rate and energy release rate,which directly give rise to the high reaction violence.Therefore,for the same threat stimulus,the more massive the charge,the higher the reaction violence,and the greater the accident hazard.Moreover,it is noteworthy that only the condition of forced ignition is considered in this study,while the influence of complex response on the final reaction violence under fast/slow cook off conditions is neglected.

Fig.5.Influence of casing size on the reaction growth after explosive charge ignition:(a)Pressure-time curve;(b)Reaction degree-time curve;(c)Pressure,charge reaction degree,and reaction violence when the casing is fractured.
As shown in Fig.6,within the range of charge size and casing thickness considered in this study,thicker casing has stronger constraint,smaller casing deformation,faster pressure growth after explosive ignition,more violent explosive reaction,and more reacting amount of explosive charge when the casing factures.By further increasing the casing radius ratioK,the corresponding internal pressure and explosive charge reaction degree when the casing fractures are calculated.As shown in Fig.6(c),largerKcauses stronger casing structure constraint,faster pressure growth,higher explosive reaction rate as well as larger pressure,explosive reaction degree,and reaction violence when the casing is fractured.
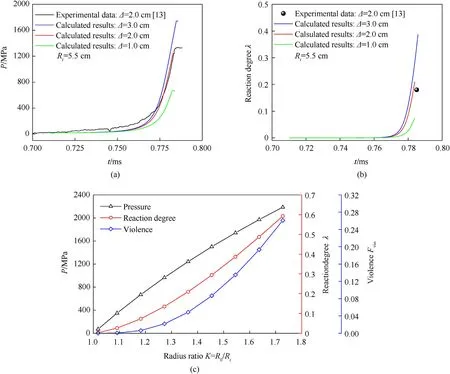
Fig.6.Influence of casing thickness on the reaction growth after explosive charge ignition: (a) Pressure-time curve;(b) Reaction degree-time curve;(c) Pressure,charge reaction degree,and reaction violence when the casing is fractured.
To further examine the influence of input pressureP0on the reaction growth after charge ignition,we still use the steel structure with spherical constraint.The internal radius of sphereRi=5.5 cm,and the wall thickness Δ =2 cm.As shown in Fig.7,under the premise of reliable ignition,lower input pressure P0causes lower crack surface area SIGand longer response time of surface combustion,which due to the long-range flow of high-temperature gas products along the cracks in explosive bulk and surface in the early stage of low pressure thus slower pressure growth,lower explosive reaction rate,and longer response time of casing deformation till fracture.This process lasts for a short time and the subsequent combustion surface area drastically increases to form a combustion network.The self-enhanced combustion can shortly eliminate the difference among the initial states of charge combustion.During the later stage of combustion,the differences of pressure growth rates and charge reaction rates are both decreased,and the internal pressure,charge reaction degree,and reaction violence remain the same when the casing is fractured.Within the scope of this paper,the input pressure has no significant influence on the final charge reaction degree and the reaction violence.
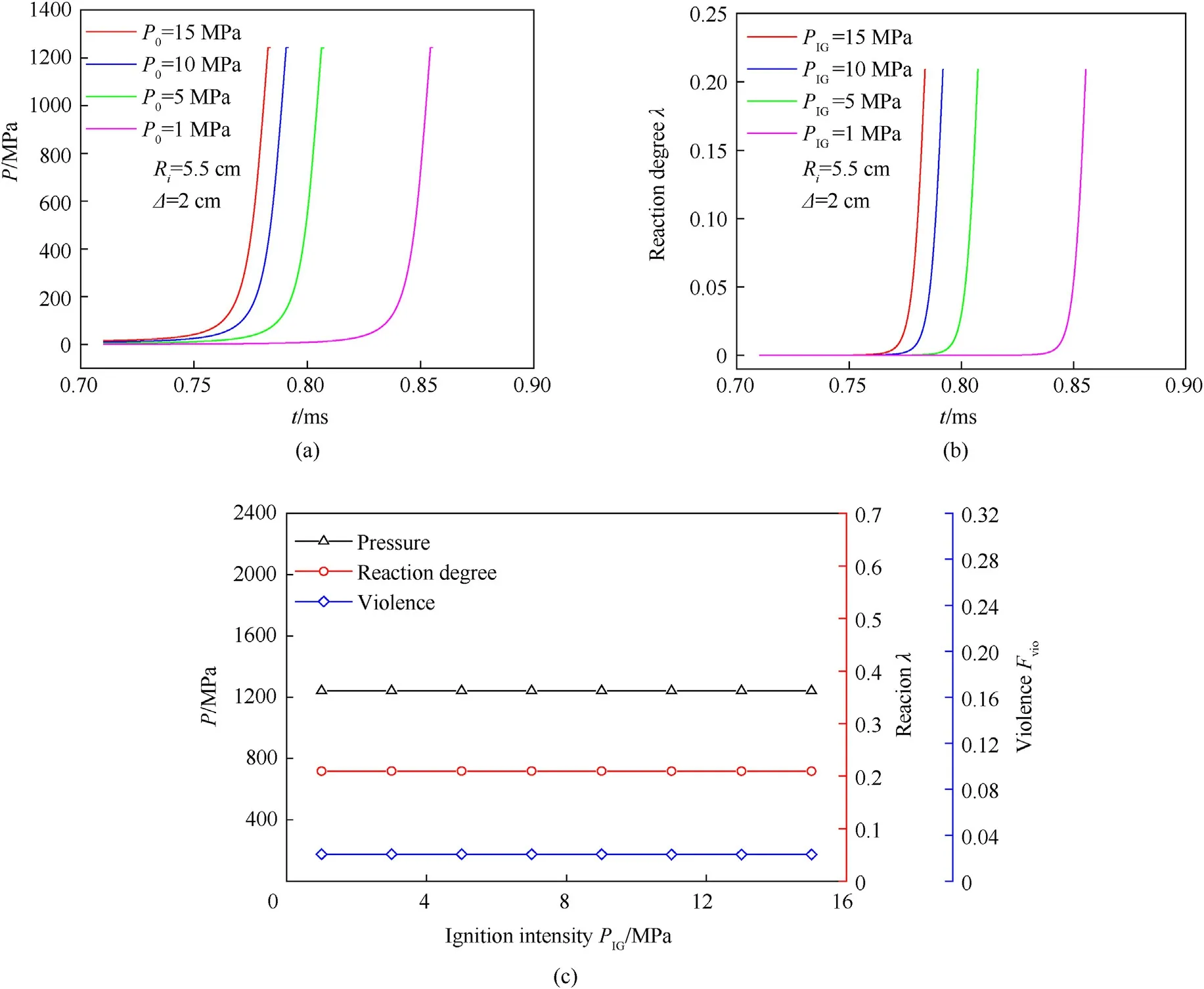
Fig.7.Influence of input pressure on the reaction growth after explosive charge ignition: (a) Pressure-time curve;(b) Reaction degree-time curve;(c) Pressure,charge reaction degree,and reaction violence when the casing is fractured.
3.Results and discussion
3.1.Reaction evolution model considering relief structure
To decrease the reaction violence of explosive charge,a relief structure is typically added on the casing.When the internal pressure of casing reaches a certain valuePcr,the relief plug is broken to release the internal pressure.According to the classic hole model for high-pressure gas leakage[26,27],when the venting hole is open,the loss rate of product mass is expressed as follows:
whereC0is the outflow coefficient;Ais the relief area;γ and Mgare the adiabatic coefficient and molar mass of ideal gas,respectively.
Hence,the total mass increase rate in the system is
Similarly,assuming that the product is a mixture of ideal gas,differentiating Eq.(13)with respect to timetand using Eq.(6),Eq.(11),Eq.(18),and Eq.(19),we get
Further,the change in the internal pressurePof casing with timetafter the venting hole is open is expressed as
Once the venting hole structure is open,the stiffness of casing constraint is decreased.The weakening factor κ should be considered to satisfyIp=κI,whereIprepresents effective stiffness of the casing.
For cylindrical casing,
To ensure that the casing strength after the hole opens meets the design requirements and to effectively control the reaction progress of charge,this model can be used for calculating the venting hole area and opening pressurePcr.The venting hole is open when the internal pressure of casing increases toPcr.By adopting the same spherical constraint and charge (see Fig.8) as mentioned before,we usePcr=20 MPa to assess the influence of different venting hole areaAon the explosive charge reaction evolution after ignition.The results show that larger venting hole areaAcauses better pressure relief effect and slower growth of internal pressure of casing.When the venting hole areaAreaches a certain value,the loss rate of gas product is larger than its production rate (gas product is accumulated in the system before the opening of venting hole),leading to the gradual decrease of casing internal pressure to zero.Therefore,by using matching method to design the break-through threshold valuePcrof venting hole structure and venting hole areaA,the loss rate of gas product becomes equal to the production rate,which ensures the stability of combustion reaction of explosive charge until the reaction is finished.
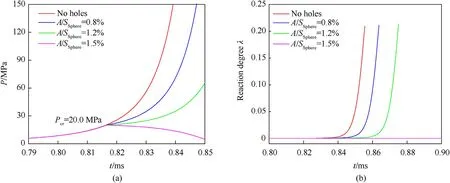
Fig.8.Influence of relief area on the reaction growth of constrained spherical charge after ignition.
3.2.Reaction evolution model considering ullage volume
To ensure the reliability of charge pressure relief in the insensitive ammunition design,ullage is typically reserved between charge and casing.Accommodate the pressure from chemical reaction.
Although this ullage volume is very small as compared to the total volume,it has a significant influence on the induction stage of explosive charge reaction.The total volumeVof explosive charge system includes explosive volumeVe,crack volumeVc,and ullage volumeVu,i.e.,
Att=0,the volume of explosive system is
It is assumed that in the combustion reaction evolution,the ullage volume remains constant,i.e.,Vu=Vu0.Hence,
Compared to Eq.(5),the expression of system modulusMis modified as
Compared to Eq.(6),the crack volume satisfies
Compared to Eq.(13),the ideal gas mixture product satisfies
Differentiating Eq.(31)with respect to timet,and using Eq.(11),Eq.(18),Eq.(19),and Eq.(30),we get
where
The variation in the pressurePwith timetconsidering the influence of ullage volume and relief structure is expressed as follows:
As shown in Fig.9,we use spherical steel casing with thickness Δ =2 cm and internal radiusRi=5.5 cm.The input pressure of PBX9501 explosive chargeP0=1 MPa.To investigate the independent influence of ullage volume on the reaction evolution of constrained explosive after ignition,the venting hole structure is not considered temporarily.The results show that larger ullage volume causes a longer induction stage in the ignition reaction,which leads to a right shift of the pressure and reaction degree-time histories.In addition,larger ullage volume is beneficial for delaying the violent reaction since the flowing space for high-temperature gas products is greatly increased,which inhibits the increase in internal pressure and extends the surface combustion time.

Fig.9.Influence of ullage volume on the reaction growth of constrained spherical charge after ignition.
4.Conclusions
In this study,an effective theoretical model was established for the evolution of CCN reactions.The proposed model was used to elucidate the effects of different factors,including intrinsic combustion rate of explosives,constraint strength,charge structure size,relief area,and reserved ullage volume,on the evolution of non-shock ignition combustion reaction of explosive charge.The main conclusions are summarized as follows:
(1) The explosive reaction evolution after ignition exhibits three typical stages: induction stage,exponential growth stage,and high-speed linear growth stage.
(2) Under the condition of geometric similarity,larger charge structure size leads to longer time for pressurization and extension of cracks.Further,the combustion is slower in the early stage,but it is more violent in the later stage.The larger the charge size,the more violent the reaction.
(3) Stronger casing constraint leads to more rapid selfenhanced combustion of high-temperature gas product,longer lasting time for the saturated combustion of crack network,more violent charge reaction,and higher charge reaction degree when the casing fractures.
(4) Lower input pressureP0triggers lower crack surface area,longer low-pressure induction stage,slower pressure growth and explosive reaction,and longer response time for casing deformation till fracture.However,for the lowamplitude ignition pressure in this work,the influence of input pressure on the final reaction degree and reaction violence of charge is not significant.
(5) Larger venting hole area causes more significant pressure relief effect.By matching design of the break-through thresholdPcrof venting hole structure and venting hole area,the loss rate of gas product can be made to be equal with its production rate,leading to stable combustion of explosive charge until it is fully reacted.
(6) Larger reserved ullage volume causes longer low-pressure induction stage,which is more beneficial for delaying the violent reaction.The ullage volume provides more space for the flow of high-temperature gas product,inhibiting the growth of internal pressure.
At present,the exploration on CCN reaction evolution model is still in primary stage.There are still much factors need to be considered,such as influenced by thermal stimuli,the evolution will be more complex.We need to further development of the CCN model on discovering the main controlling factors in explosive ignition reaction evolution under thermal stimuli.Meanwhile,we also need to build the whole-process model on the reaction evolution of thermal stimuli ignition-combustion.Overall,this study provides useful insights on the CCN reaction evolution for highly confined solid explosives,contribute to the safety design of ammunition,and we hope it can serve as a theoretical basis for quantitatively characterizing the explosives reaction degree and violence evaluation under thermal stimuli in the future.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No.12002044) and the National Key Laboratory of Shock Wave and Detonation Physics (Grant No.6142A03192007).

Appendix B.Stress field,displacement field,and expression of generalized equivalent stiffness I for elastoplastic deformation of medium thick/thick-wall casing with different shapes
- Defence Technology的其它文章
- Deep learning-based method for detecting anomalies in electromagnetic environment situation
- Impact point prediction guidance of ballistic missile in high maneuver penetration condition
- Real-time localization for underwater equipment using an extremely low frequency electric field
- Numerical simulation of flow field characteristics and theimprovement of pressure oscillation of rotating detonation engine
- Comparative investigations of ternary thermite Al/Fe2O3/CuO and Al/Fe2O3/Bi2O3 from pyrolytic,kinetics and combustion behaviors
- Adaptive saturated tracking control for solid launch vehicles in ascending based on differential inclusion stabilization

