基于迁移学习的四旋翼无人机性能驱动的故障检测

薛 山, 李琳琳,2*, 乔 梁,2, 丁梦龙

1. 北京科技大学自动化学院, 北京 100083

2. 工业过程知识自动化教育部重点实验室, 北京 100083

0 引 言

近年来,随着集成电子技术和自动控制技术的发展,无人机技术已成为一种有效的主流应用工具.无人机在搜索、救援、遥感、地理研究以及各种军事和安全应用等任务中发挥着重要的作用.目前,固定翼和多旋翼无人机是最受关注的类型.与固定翼不同,多旋翼无人机可以实现垂直起降和悬停,非常方便监视、精准农业、电力线路自动监测和交付等应用[1].本文主要研究四旋翼无人机的故障检测问题.由于控制器失效、零部件磨损或其他原因,无人机可能发生故障,导致无法准确完成任务.因此,需要及时对无人机进行故障检测.

针对四旋翼无人机的非线性系统,提出了基于性能驱动的故障检测方法.其中,性能指标的设计是基于性能的故障检测方法的核心部分.目前已经出现了许多种设计性能指标的方法.例如文献[2]中提出的Harris指标,文献[3]提出的线性二次高斯(LQG)基准.随着数据处理能力的不断提高,涌现出了越来越多的基于性能的数据驱动故障检测方法,例如基于数据融合、基于张量空间和基于迭代学习等方法[4-7].目前,基于数据驱动的方法已经成为主流.然而,数据驱动的方法需要大量的数据,当四旋翼无人机到达一个新的重力场时,会使得无人机的数据分布相比于之前的数据分布发生了变化.因此,现有的故障检测系统可能无法直接使用,重新收集足够的数据耗时耗力,从而使得在此新重力场下无人机的故障检测面临着数据稀缺的问题.

迁移学习是机器学习的一个分支,旨在通过一个或多个相关但不同的应用场景中学习共同的知识,来帮助提高目标领域的性能,这已经被证明是解决上述问题的有效方法[8].迁移学习在故障检测和诊断领域也受到了广泛的关注.文献[9]通过保留和重用存储在神经网络中的先前知识,提出了一种用于监测动态系统中传感器故障的迁移学习方法.文献[10]通过迁移学习自适应方法对基于残差网络的故障诊断模型进行参数重调,实现了当前在轨的航天器故障诊断.

根据前面所述背景,提出了一种基于迁移学习的非线性四旋翼无人机性能驱动的故障检测方法,首先通过神经网络拟合无人机性能评价函数,结合Bellman方程以残差的形式设计检测指标.针对无人机在新的重力场中数据不足的问题将源域神经网络中的浅层知识迁移到目标域中.最后,源域数据通过布雷格曼散度在子空间中对齐目标域数据,再通过神经网络将其反映射到目标域中,并得到检测的阈值,最终实现了无人机的故障检测.本文所提出基于迁移学习的性能驱动的故障检测方法与其他方法不同,本文方法专注与任何引起系统性能下降的故障,而后者更多专注于一类故障,同时,通过神经网络的拟合来完成故障检测,与基于模型的故障检测方法相比,本文方法无需知道任何的系统动力学知识.考虑数据不足到的问题引入迁移学习,在数据对齐时与其他迁移学习中常用的MMD距离不同,所采用的布雷格曼散度是一种非线性的度量方式,避免了使用MMD距离可能会出现的样本外的问题,另外,在迁移学习中我们不仅仅只关注于域之间的差异,也考虑到了域中数据间的联系,通过构造最近邻图来保证迁移后数据之间依然保持有相似信息.

1 四旋翼无人机模型与迁移学习基础知识

1.1 四旋翼无人机模型

四旋翼无人机顾名思义有4个旋转翼,呈十字形分布,四旋翼无人机的中心在其几何中心上,结构如图1所示.

图1 四旋翼无人机结构图Fig.1 Structure diagram of quadrotor Unmanned Aerial Vehicle(UAV)

获得无人机的数学模型首先要建立两个基本坐标系,地理坐标系(OEXEYEZE)和机身坐标系 (OBXBYBZB),如图2所示.

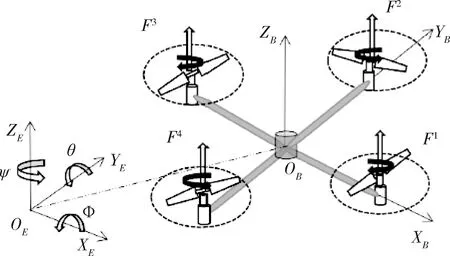
图2 四旋翼无人机坐标系示意图Fig.2 Quadrotor UAV coordinate system diagram

为了确定无人机的姿态,定义俯仰角θ、横滚角φ以及偏航角ψ3个欧拉角.

从地理坐标系到机体坐标系的旋转矩阵为T,如式(1)所示

(1)

其中,T12=sinθsinφcosψ-sinψcosφ,

T13=sinψsinφ-sinθcosφcosψ,

T22=sinθsinφsinψ+cosφcosψ,

T23=sinθsinψcosφ-sinφcosψ.

无人机的所有动力由4个旋翼上的电机产生,每个电机产生向上的力,升力的大小与旋翼旋转角速度成正比,各升力扭矩的大小如式(2)所示

(2)

式中,kt为升力系数,kd为扭力系数,ωi为4个旋翼的旋转速度,U1为垂直方向输入量,U2为横滚控制输入量,U3为俯仰控制输入量,U4为偏航控制输入量.

根据牛顿-欧拉公式,假设四旋翼无人机处于悬停或无风环境下小角度飞行,可以得出无人机的动态方程为

(3)

式中,g为重力加速度,m为四旋翼无人机的质量,JX、JY和JZ分别是四旋翼无人机绕X轴、Y轴和Z轴的转动惯量.

1.2 迁移学习

迁移学习是机器学习的一个分支,它属于一种学习范式.该方法应用于两个或多个不同但相似的领域,其侧重点在于如何迁移或重用之前已经学习到的知识来处理新任务.而迁移学习的成功实现则少不了神经网络的应用.

迁移学习的应用大多离不开神经网络,神经网络是一个多层的结构,它较浅的层提取低级别的特征,而较深的层可以学习特定于不同应用领域更为抽象的表示[11],根据这个特点,神经网络浅层提取到的较低层次的知识可以进行迁移,只需要在目标域中学习较高层次的知识,从而提高所需模型的性能.另外,通过一种分布度量来衡量源域与目标域的相似性,找到一种映射使得映射到子空间的源域与目标域的分布接近于相同,从而借助子空间来完成目标域的相关任务[12-13].

由于使四旋翼无人机到达执行任务的空间位置是通过旋翼旋转产生推力完成的,而旋翼的旋转产生的推力受无人机所处重力场的影响.当无人机到一个新的重力场执行任务时,无人机的故障检测面临着数据不足的问题,因此,本文利用迁移学习实现无人机在新的重力场的故障检测.

2 基于迁移学习的性能驱动故障检测系统

2.1 离线阶段故障检测系统的设计

选择四旋翼无人机的状态变量、输出和输入分别为

(4)

四旋翼无人机的动态方程如等式(4)所示,它是一个具有强耦合、非线性的特点的系统,也是一个灵敏度非常高的系统,这就要求当无人机发生故障时需要及时的检测出来,通常采用系统的输入输出构成的函数作为一个系统的性能评价函数

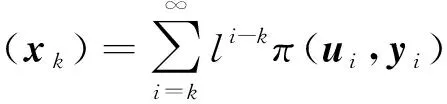
(5)

式中,l为衰减因子,π(ui,yi)≥0表示为奖励函数,定义为系统输入输出信号的二次型的形式,如下所示:

(6)

式中,Q和R为正定矩阵.

显然,对于每个可允许的控制策略,都会有对应的性能评价函数(5)从应用的角度来说,保证系统运行以实现所需的性能是至关重要的,在实际中,过程操作和系统参数的变化,以及系统组件的老化,执行器传感器故障都会导致系统发生故障,进而可能改变评价函数(5)的值,因此采用上述评价函数通过性能实现无人机的故障检测是合理的.

众所周知,对于给定的反馈控制策略.在无故障情况下的性能评价函数满足以下Bellman方程:

ϑ(xk)=π(ui,yi)+lϑ(xk+1)

(7)

通常,四旋翼无人机系统的值函数包含高阶非线性,为了通过评估性能来进行故障检测,通常会用存在一组稠密基函数的Weierstrass高阶近似定理来逼近值函数[13],如下所示:

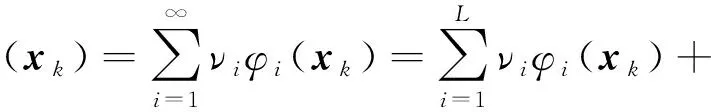
(8)

其中,Φ(xk)=[φ1(xk)φ2(xk) …φL(xk)]表示基向量,N=[ν1ν2…νL]表示权重系数矩阵,误差ε(xk)随着保留项L趋于无穷而趋于0.事实上,性能指标(8)是单层神经结构,然而在神经网络的研究中,浅层神经网络的神经元需要指数式的增长才有可能达到深层神经网络的拟合效果[11].同时在文献[15]中实现了以系统的I/O数据为输入而不是传统的以系统的状态为输入的方法来计算值函数.因此在基于性能驱动的故障检测中的近似函数被一个以系统I/O数据为输入的深层神经网络来代替.当无人机出现故障时,Bellman等式(7)不再成立,因此,根据这个特点,出于检测的目的在时刻k处定义基于性能驱动的故障检测指标

κ(k)=|Λ(zk)-π(uk,yk)-lΛ(zk+1)|

(9)

其中,zk=[ukyk]T表示四旋翼无人机系统的输入输出数据, Λ(·)表示神经网络.明显可以看出系统任何的变化都会引起检测指标(10)的变化,由此执行以下检测逻辑

(10)

其中,δ>0为检测指标的容忍阈值,故障检测可以通过式(9)和(10)来执行.对于故障检测指标中所采用的神经网络结构如图3所示.

图3 神经网络结构图Fig.3 Neural network structure diagram

图3中,x为神经网络的输入,w为权重系数,n为当前神经元激活前的输出,s为神经元的数量,a为当前神经元激活后的输出,y为神经网络的输出.在神经网络中,选择均方误差作为损失函数,双曲正切函数作为激活函数,双曲正切函数是在sigmoid函数上改良而来的,有着比sigmoid导数更容易计算,求最优解更迅速等优点[16].最后通过反向传播更新神经网络的权重系数,以最右侧路径为例,从输出层到输入层的每一层神经元的权重系数更新规则如下:

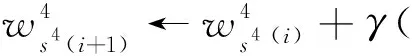
(11)

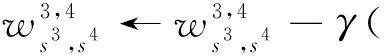
(12)

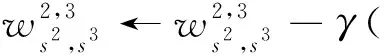
(13)

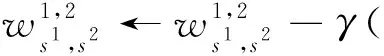
(14)

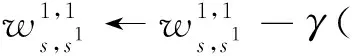
(15)

其中,ϑ表示真实的值函数,每个字母上标表示神经网络层的索引,下标为所在层的神经元索引,γ表示学习率.经过对神经网络的训练和更新,可以通过无人机系统的输入输出数据实现无故障情况下的值函数拟合.

2.2 故障检测系统的迁移

基于模型的方法是迁移学习中最常用的方法.它侧重于假设源域和目标域之间在模型层面共享一些共同知识,并通过从源域迁移这些共享知识到目标域中,从而提高目标域模型的性能[17].在神经网络中,浅层网络提取到的知识更为一般,而越深层提取到的知识越为特殊.一般来说,神经网络可以划分为3部分:第1部分提取的特征通常非常一般,第2部分包含了一般的特征以及独有的特征,第3部分提取的特征是本领域独有的特征.因此,将第1部分的参数冻结,并与第2部分的参数迁移到目标域中的模型中,第2部分的参数再进行微调,而目标域中的第3部分则需要重新训练.迁移过程如图4所示.

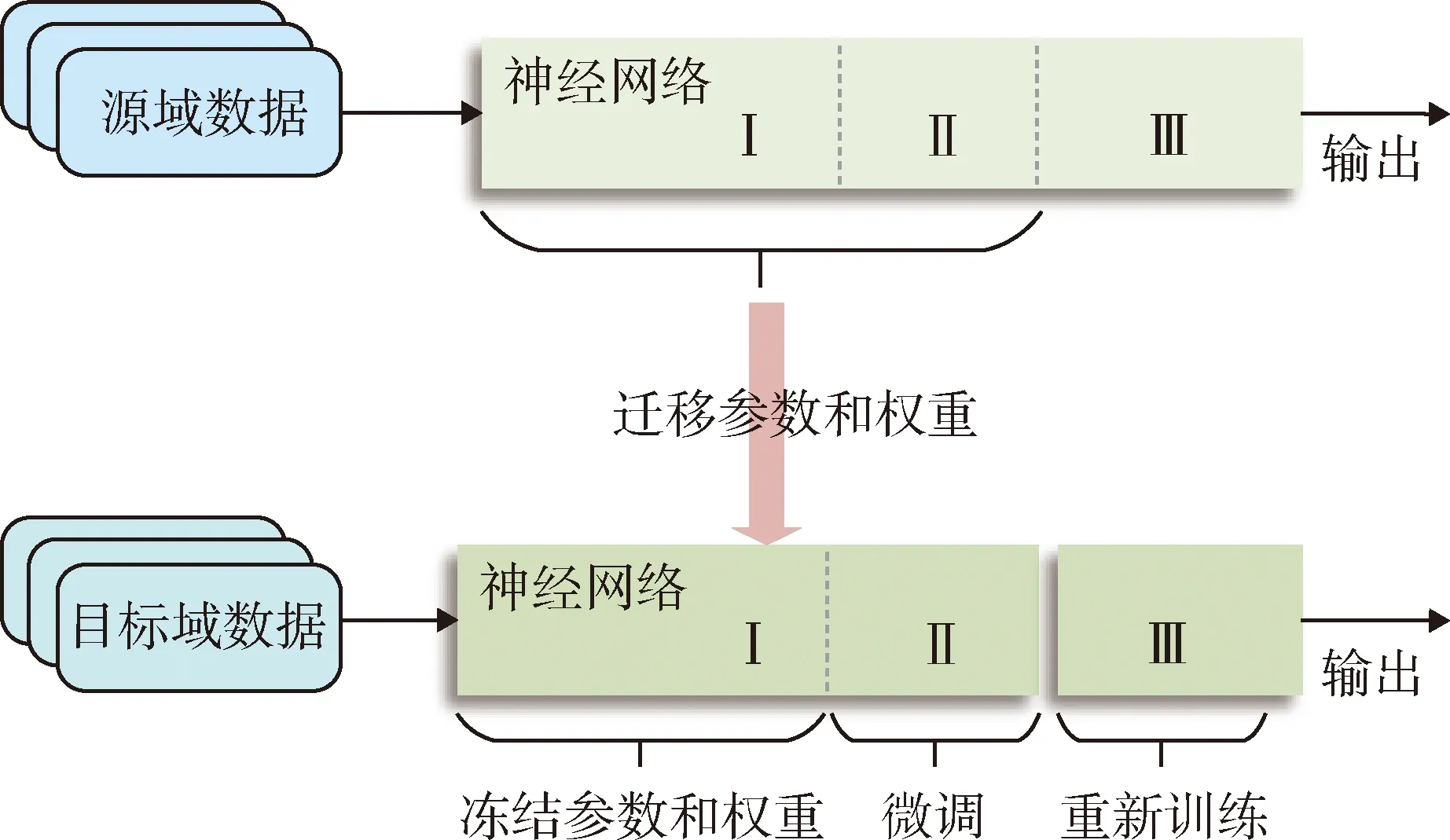
图4 神经网络迁移过程图Fig.4 Neural network transfer process diagram

3 阈值设定和在线检测

通过式(10),可以看出对无人机的故障检测关键在于设置一个合理的阈值.将这个阈值定义为检测指标的最大值.然而,在目标域中,数据稀缺,仅仅通过目标域训练出的阈值不具有说服力.因此,采用迁移子空间的方式,将源域与目标域在子空间中对齐,然后将子空间中的数据反映射回目标域,从而最终获得阈值.定义的阈值如等式(16)所示

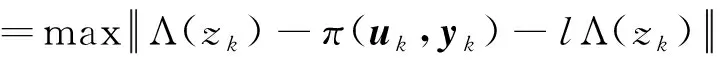
(16)

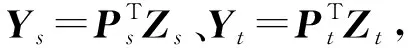
为了在子空间中对齐源域和目标域的数据样本,需要一个距离度量来衡量两个域之间的差异.在本文中,采用布雷格曼散度作为子空间中Ys和Yt的距离度量,如式(17)所示

(17)

其中,GΣ表示高斯核,对于布雷格曼散度具体推导可以参考文献[18].目标是通过映射矩阵Pt,Ps使子空间中源域与目标域的布雷格曼散度最小.

在将数据映射到子空间时,为了保证数据之间的局部相似信息不被丢失,引入拉普拉斯正则化项[19],通过构造最近邻图来表示单个域中两点zi和zj之间的相似性,从数学的角度,该公式可以表示为

(18)

其中,Wij表示数据点zi与zj之间相似性的邻接矩阵,可以通过等式(18)计算,式中Nk(zi)、Nk(zj)分别表示zi和zj的k近邻集合,t一般取为均方距离

(19)

在将数据映射到自己空间时,需要提高单个域中点之间的相似性,可以通过最小化公式(18)来实现,优化函数可以写为

(20)

式中,L为拉普拉斯矩阵,可以通过L=G-W计算,其中Gij为度矩阵,通过式(21)计算

(21)

通过最小化布雷格曼散度使两个域之间的分布接近,同时最小化拉普拉斯矩阵来保持数据之间的局部相似性,为了保证映射矩阵不为零矩阵,需要对两个映射矩阵施加正则化约束,那么最终的的优化函数为

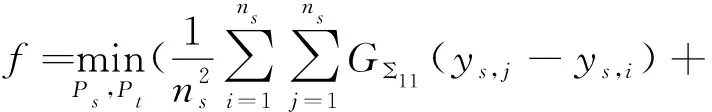
(22)

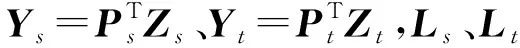
(23)

(24)

最后,通过梯度下降来求解两个映射矩阵Ps和Pt,即

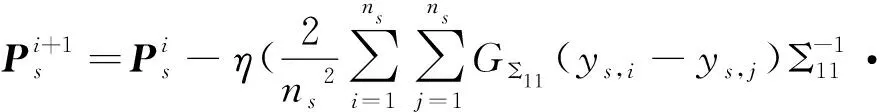
(25)

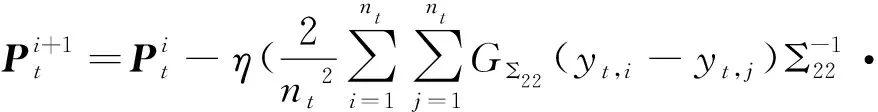
(26)

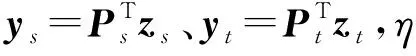
获得阈值后,使用检测逻辑(10)对到达新重力场的无人机进行故障检测.提出的基于迁移学习的四旋翼无人机性能驱动的故障检测方法的步骤如算法1所示.

4 实验验证

在本章中,通过四旋翼无人机在到达一个新的重力场下设置两种故障来验证提出方法的有效性.

对于四旋翼无人机状态方程如第1章节中式(3)所示,其中四旋翼无人机的输入为u=[U1U2U3U4],输出为y=[XYZ],四旋翼无人机的各个参数值如表1所示。

本文中四旋翼无人机的控制器采用文献[20]中的PID控制器,并将采样时间设置为0.02 s.通过算法1实现对无人机到达新的重力场的故障检测时,需要在一个低维子空间中对齐源域数据和目标域数据.选择一个三维子空间,在该空间中归一化后的源域数据与目标域数据的分布如图5所示.

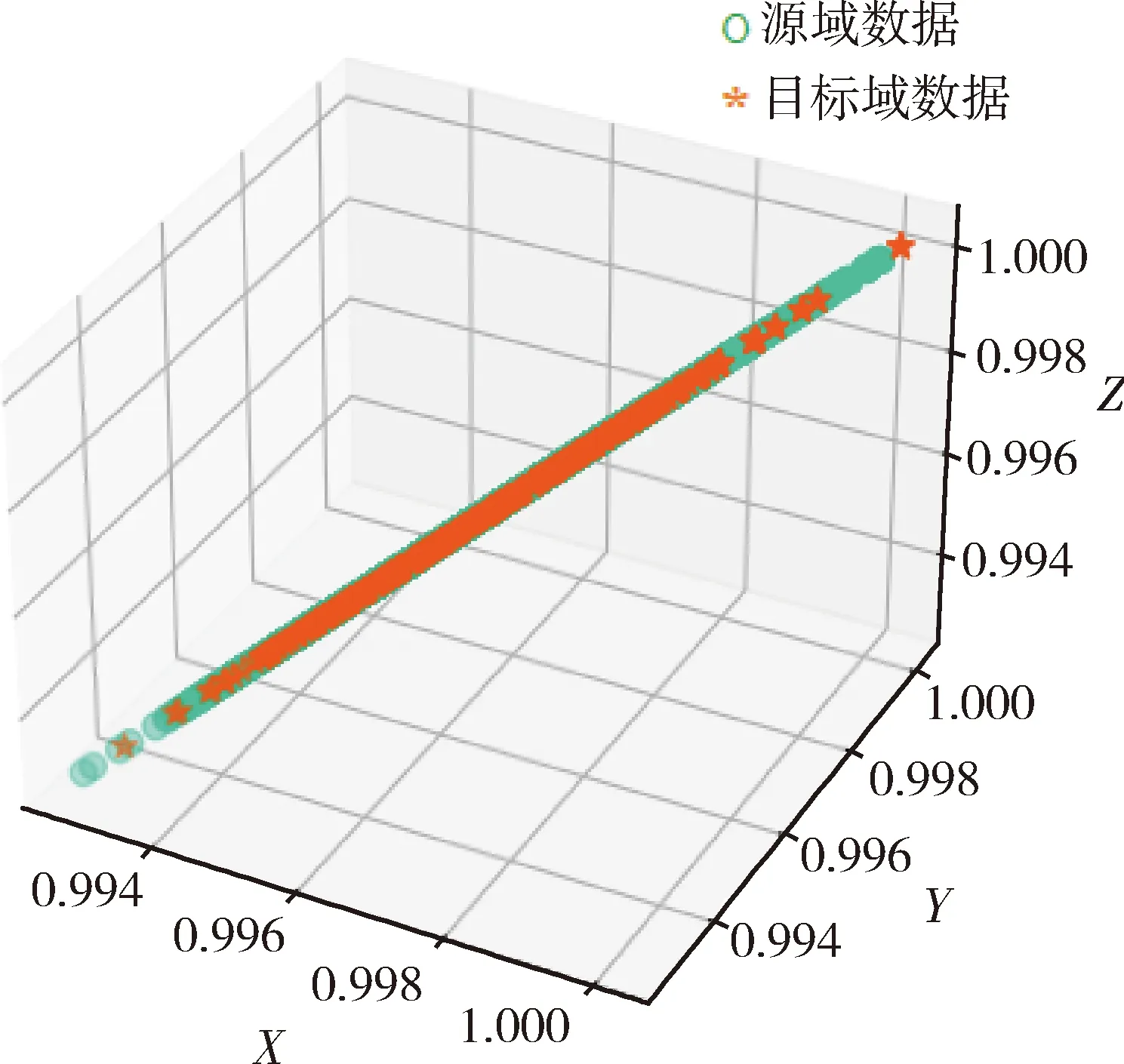
图5 子空间数据分布图Fig.5 Subspace data distribution diagram

在神经网络的梯度下降训练中,算法1步骤2神经网络的训练迁移与不迁移神经网络损失函数对比如图6所示,迁移学习后神经网络训练比不迁移收敛的更快,在故障检测中,由于数据稀缺,通过式(16)获得的检测阈值不具有一般性,通过将数据迁移解决数据稀缺的问题,从而使阈值更具说服力.

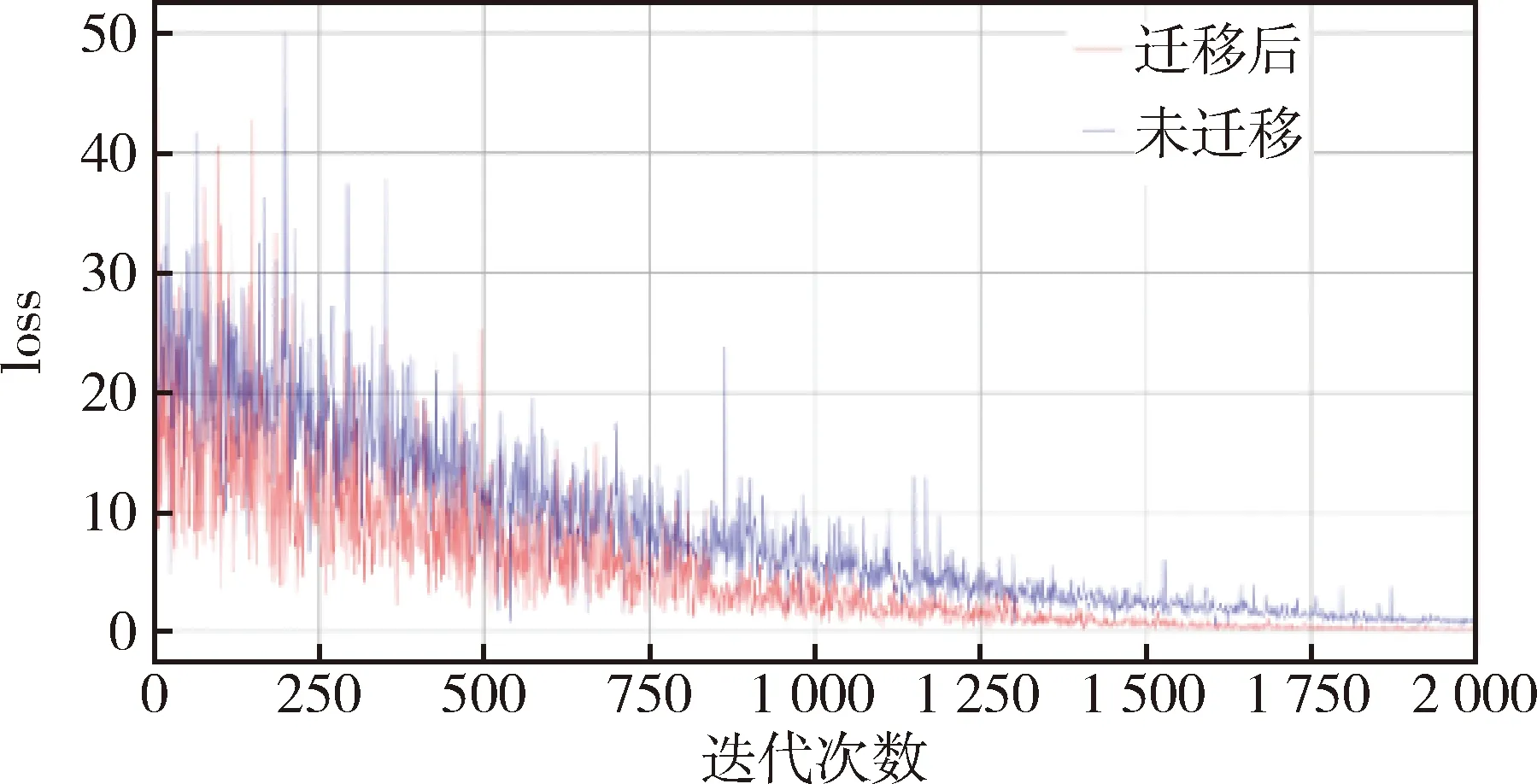
图6 迁移与未迁移损失函数对比Fig.6 Comparison of loss function between transfer and non-transfer

首先考虑在四旋翼无人机的执行器发生故障,模拟现实中四旋翼无人机的推力系统发生故障,我们设置在第2 000个样本时发生故障,检测结果如图7所示.

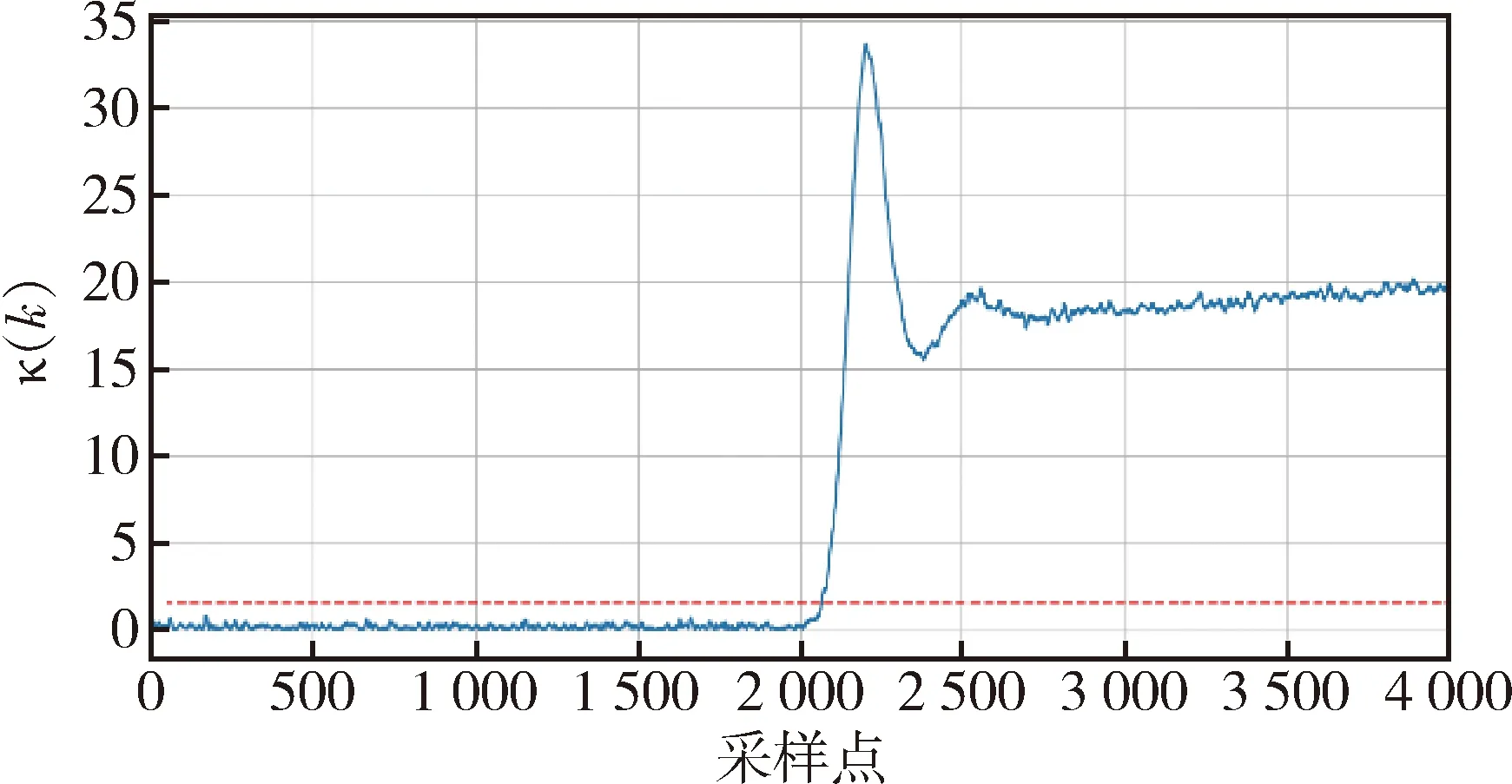
图7 执行器故障检测结果Fig.7 Fault detection result for the actuator

其次考虑在四旋翼无人机的内部参数发生变化,模拟现实中四旋翼无人机的内部某个元器件发生故障,同样设置在第2 000个样本时发生故障,检测结果如图8所示.

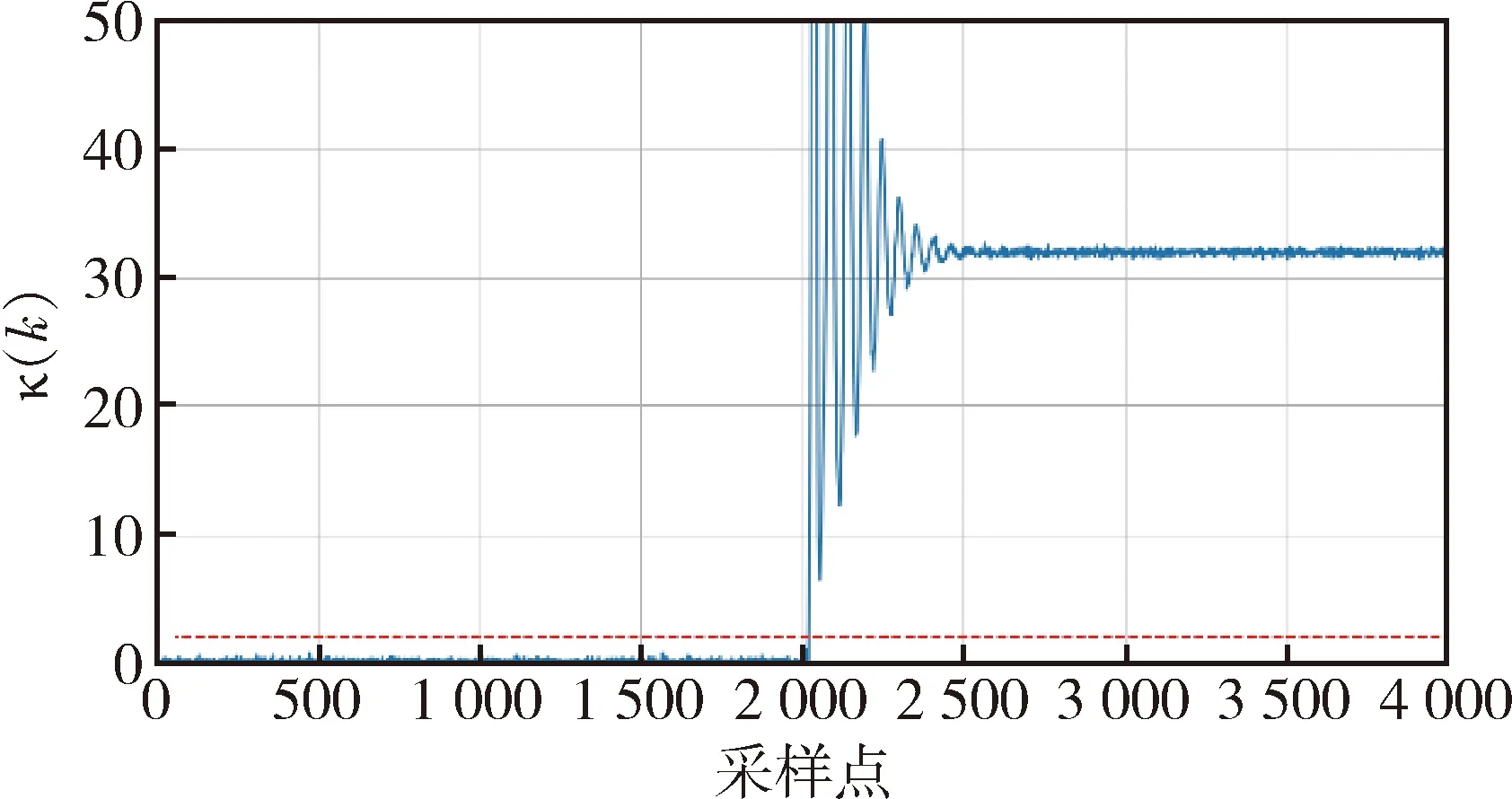
图8 执行器故障检测结果Fig.8 Fault detection result for the actuator

上述两个实验验证了本文方法的有效性.通过神经网络拟合了四旋翼无人机系统的值函数,并通过迁移学习解决了在目标域中数据稀缺的问题.当无人机到达一个新的重力场执行任务时,能够实现基于性能驱动的四旋翼无人机故障检测.

5 结 论

本文旨在实现四旋翼无人机的性能驱动故障检测方法,通过神经网络拟合无人机系统的性能评价函数.同时,考虑到无人机到达一个新的重力场数据稀缺的问题,通过子空间迁移和布雷格曼散度方法完成数据对齐,神经网络的参数迁移以及阈值的设定,从而实现了基于迁移学习的无人机性能驱动故障检测.目前,对于四旋翼无人机的故障检测在到达一个新重力场的情况尚未受到足够的关注.而本文方法考虑到了这种情况,未来的工作将集中在研究如何在无人机发生故障后实现性能恢复.