基于ANSYS 的一种长大件工装底座的静态结构分析

饶 金， 陈川龙

（海军装备部驻武汉地区第八军事代表室， 湖北 武汉 430084）

0 引言

工件置于工装底座引起底座变形，在工装底座设计合理时，其形变量较小，能够满足使用要求。工装底座设计时，可以通过线性静力学方法分析计算其形变量。设计合理的工装底座在满足变形量要求的前提下，应使用尽可能少的材料。

对于复杂的工装底座，通常无法通过正向方法设计，一般采用迭代法设计，即先初步设计一个工装底座，对其形变量进行计算，根据计算所得到的形变量和应力集中情况，优化工装底座设计，再进行计算，依次类推，从而得到符合要求的工装底座设计方案。

对于梁、杆、板等简单的结构件，可通过材料力学的方法得到形变与应力的解析解。实际的工装底座结构复杂，通过解析方法进行计算较困难，有时甚至不可能。通过计算机仿真的方法，将分析对象离散化，形成一组代数方程，通过计算机对代数方程迭代计算，可以得到满足精度要求的数值解，从而提高了复杂结构件的形变计算精度[1]。

计算机仿真主要是以有限元法、有限差分法、有限体积法以及无网格法对仿真对象进行求解，目前有限元法应用最为广泛。基于有限元技术，已形成了规模广大的商业软件市场，主要的有限元软件厂商有ABAQUS、ADINA、ALGOR、ANSYS 等。ANSYS 软件是一种融结构、热力学、流体力学、电磁学和声学于一体的大型通用有限元软件，广泛应用于水利、铁路、造船、汽车等领域。本文基于ANSYS 软件Workbench 平台的static structure 模块，对工装底座进行静力学分析，通过对比不同网格划分策略下的仿真结果，验证了优良的网格划分可以计算出准确的形变量。

1 静力学有限元计算方法

有限元法的基本思想就是离散化，即将一个原来连续的物体划分为有限个单元，这些所划分的单元通过有限个节点相互连接，承受与实际载荷等效的节点载荷，并根据力的平衡条件进行分析，然后根据变形协调的条件把这些单元重新组合，变成能够整体进行综合求解的模块，从而使一个连续的无限自由度问题变成离散的有限自由度问题。

1.1 基本思想

在工程或物理问题的数学模型（基本方程、基本变量、求解域和边界条件等）确定以后，有限元法作为对其进行分析的数值计算方法，可简单概括为如下三点[2]：

1）将一个连续体或表示结构的求解域离散为若干个子域（单元），并通过它们边界上的节点相互连接为一个组合体。

2）用每个单元内所假设的近似函数来分片地表示全求解域内待求解的未知场变量。而每个单元内的近似函数由未知场函数（或其导数）在单元各个节点上的数值和与其对应的插值函数来表达。由于在连接相邻单元的节点上，场函数具有相同的数值，因而将它们作为数值求解的基本未知量。因此，求解原待求场函数的无穷多自由度问题转换为求解场函数节点值的有限自由度问题。

3）通过和原问题数学模型（例如边界条件、基本方程等）等效的加权余量法或变分原理，建立求解基本未知量（场函数节点值）的常微分方程组或代数方程组。此方程组成为有限元求解方程，并表示成为规范化的矩阵形式，接着用相应的数值方法求解该方程，从而得到原问题的解答。

1.2 计算方法

静态结构分析主要考虑结构在静力作用下的变形、约束反力、应力和应变的分布情况等，不考虑惯性和阻尼的影响。

根据弹性力学和有限元理论得知，在结构中取微小单元进行受力分析，可得到单元的平衡微分方程、几何方程和物理方程[3-7]。

平衡微分方程如式（1）所示。

式中：τ 为剪应力；σ 为单元应力；X、Y、Z 为单元的体力分量。

几何方程如式（2）所示。

式中：ε 为单元应变；γ 为剪应变；u、v、x 为位移分量。

物理方程如式（3）所示。

式中：E 为弹性模量；μ 为泊松比。

利用微分方程和边界条件，即载荷和约束，可以利用有限元软件求得有限个单元点处的变形与受力情况，根据节点位移和上述平衡方程可以求得应力、应变分布。

1.3 基本过程

在ANSYS Workbench 平台中进行静态结构分析的基本过程如图1 所示。

图1 有限元法静态结构分析的基本过程

2 计算模型与材料特性

2.1 工装底座结构

已知长大件长约10 m，宽约0.4 m，质量3 t。工件尺寸较长、重量较大，为减小工件变形，需为工件专门制作工装底座，工件通过非连续平面垂直置放于工装底座上。重力作用下工装底座未置放工件时最大变形不允许超过7 mm，重力作用下工装底座置放工件后最大变形不允许超过10 mm，综合应力即von-Mises应力不允许超过材料屈服强度的90%。为减轻重量，工装底座主要通过钢板拼焊构成，经多轮优化，设计完成后的工装底座结构如图2 所示。

图2 工装底座结构

工装底座由底座主体和支座两部分组成，底座主体由端板、上支撑板、下支撑板、上底板、中底板、下底板、上肋板、下肋板、接触面板、加强板和接轴组成，接轴通过M16 螺栓与端板连接，预紧力36 kN。上支撑板、下支撑板、上肋板、下肋板、加强板对称布置，在不降低结构强度的情况下从而有效降低底座重量，上肋板共34 块，单边17 块；下肋板共42 块，单边21 块；加强板42 块，单边21 块。接触面板22 块，单边11块，面积大小不等，根据工件设计，工件存放在接触面上，工件重力均匀作用在接触面板上表面。支座与地面接触，由钢板、限位轮和支轴组成，支轴与限位轮焊接在一起，限位轮通过支轴与钢板槽接触支撑在钢板上。底座主体通过接轴与支座限位轮接触支撑在支座上。底座主体钢板、支座钢板通过焊接成为一体。

2.2 材料参数

工装底座由结构钢制作，其密度为7 850 kg/m3、弹性模量为200 GPa、泊松比为0.3，钢板、接轴、限位轮、支轴屈服强度为250 MPa，螺栓屈服强度为345 MPa。

2.3 有限元模型

2.3.1 对称设置

工装底座为对称结构，为减小计算规模、提高计算速度，用对称面从中间剖分，取一半计算，剖分后的计算区域如图3 所示，虚线框住部分为对称面。

图3 工装底座对称面

2.3.2 连接设置

限位轮与支座、支轴与支座、支轴与接轴、接轴与底座主体钢板设置为有摩擦接触，摩擦系数0.15，其他通过焊接连接在一起的钢板设置为绑定连接。

2.3.3 网格划分

为比较网格划分质量对计算结果的影响，采用两种方案划分网格。

1）方案1：扫掠体均采用6 面体网格，扫掠方向至少划分2 层网格，非扫掠体采用4 面体网格，选用合适的网格控制尺寸，避免出现尖锐网格，适当提高网格数量。

2）方案2：均采用4 面体网格，选用合适的网格控制尺寸，避免出现尖锐网格，同时适当减少网格数量。

两种方案划分后的网格如图4 所示，方案1 共有208 969 个单元、325 009 个节点，方案2 共有135 029个单元、265 933 个节点。方案1 的网格划分更为细致，相比方案2 具有更多的单元格与节点。

图4 网格划分

2.3.4 计算载荷及边界条件

载荷及边界条件如下：重力载荷，标准地球重力加速度，9.806 6 m/s2；固定支撑，支座底面固定支撑约束；螺栓预紧力，接轴与底座主体钢板通过螺栓连接，螺栓预紧力36 kN；工件作用力，工件质量3 t，均匀分布在底座接触面上。

2.3.5 分析设置

为提高计算模型的收敛性, 根据实际加载情况，将分析过程分为以下两步，第一步为施加重力载荷、固定支撑约束、螺栓预紧力，第二步为施加工件作用力载荷。

3 变形与应力分析

分别对工装底座在重力作用下、3 t 工件压力载荷与重力共同作用下的变形与应力进行分析。

3.1 变形分析

ANSYS 软件可以计算出每一步的结果，第一步未施加工件作用力载荷，计算结果即为重力作用下的变形结果。方案1 计算的最大总变形为6.390 8 mm，位于底座主体上表面，从两端到中间变形逐渐增加。方案2 计算的最大总变形为6.599 5 mm，位于底座主体上表面。两种方案计算得到的最大变形略有不同，出现位置相同，从两端到中间变形量逐渐增加，与预期一致，变形云图如图5 所示。

图5 重力作用下的工装底座变形（mm）云图

重力作用下各组件最大变形如表1 所示。

表1 重力作用下组件最大变形 单位：mm

3 t 工件压力载荷施加完成后，方案1 计算的最大总变形为8.985 6 mm，位于底座主体上表面，从两端到中间变形逐渐增加。方案2 计算的最大总变形为9.260 7 mm，位于底座主体上表面。两种方案计算得到的最大变形略有不同，出现位置相同，从两端到中间变形逐渐增加，与预期一致，变形云图如图6 所示。

图6 3 t 压力载荷与重力作用下变形（mm）云图

3 t 工件压力载荷与重力共同作用下，各组件最大变形如表2 所示。

表2 3 t 工件压力载荷与重力作用下组件最大变形 单位：mm

3.2 应力分析

重力作用下，方案1 计算的最大应力为291.13 MPa，位于螺栓根部，方案2 计算的最大应力为279.22 MPa，位于螺栓根部；两种方案计算得到的最大应力有较大差异，虽然均位于螺栓根部。螺栓应力云图如图7 所示。

图7 重力作用下螺栓应力（MPa）云图

重力作用下，各组件最大应力如表3 所示。

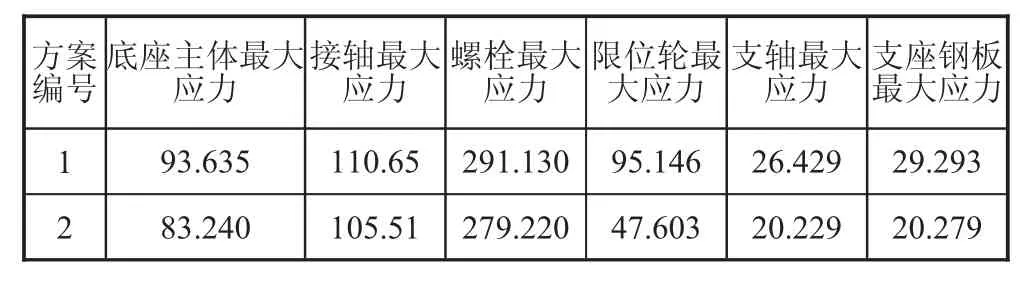
表3 重力作用下组件最大应力 单位：MPa

3 t 工件压力载荷施加完成后，方案1 计算的最大应力为301.84 MPa，位于螺栓根部；方案2 计算的最大应力为281.38 MPa，位于螺栓根部。两种方案计算得到的最大应力有较大差异，虽然均位于螺栓根部。螺栓应力云图如图8 所示。

图8 3 t 压力载荷与重力作用下螺栓应力（MPa）云图

3 t 工件压力载荷与重力共同作用下，各组件最大应力如表4 所示。

表4 3 t 工件压力载荷与重力作用下组件最大应力 单位：MPa

施加3 t 工件压力载荷后，两种网格划分方案计算得到的工装底座变形量与应力均显著增加，最大变形、最大应力出现的位置相同，与预期一致，验证了仿真模型的正确性。重力作用下，两种网格划分方案计算得到的最大变形均满足不大于7 mm 的要求。3 t 工件压力载荷与重力共同作用下，两种网格划分方案计算得到的最大变形均满足不大于10 mm 的要求。3 t工件压力载荷与重力共同作用下，工装底座各组件应力最大，螺栓最大应力301.84 MPa，为材料屈服强度345 MPa 的87.49%；其他组件最大应力134.78 MPa，为材料屈服强度的53.91%。最大应力均未超过材料屈服强度的90%，并有一定的安全裕量。仿真结果表明了工装底座设计的合理性。

两种网格划分策略计算得到的各组件的最大变形、最大应力在数值上有一定差别。对于结构变形，方案1 计算的工装底座主体部分变形小于方案2，支座部分变形大于方案2；对于应力，方案1 计算的各组件最大应力均大于方案2，其中底座主体部分，两种方案差别较小；支座部分，相对差距较大。精细的、高质量的网格划分更能精确地反映物体的实际形状，接轴与限位轮通过圆柱面摩擦接触，精细的、高质量的网格划分更能模拟真实的力的传递效果，因此方案1计算结果更接近于真实情况。

4 结语

通过两种网格划分方法对工装底座进行了有限元分析，结果表明，在重力作用下、3 t 工件压力载荷与重力共同作用下，底座的最大的变形与最大应力均满足要求，说明了工装底座设计的合理性。

网格划分方法对有限元计算结果有较大的影响，合理的网格划分更能精确反映实际情况。网格划分时，对于扫掠结构，尽量采用6 面体网格，在满足计算速度和存储要求的前提下，适当增加网格数量，避免出现尖锐网格，可以获得更精确的计算结果。