炼化装置闸阀内漏去噪及声识别技术研究*

王 琼,苟云峰,李庆润,朱 亮,刘名杨,来子琴,杨 进,肖安山

(1.化学品安全全国重点实验室,山东青岛 266104 2.中石化安全工程研究院有限公司,山东青岛 266104 3.重庆大学,重庆 400044)

0 前言

阀门作为一种通用的控制流体介质输送的设备,被广泛用于石油、化工、天然气、核电等行业。然而阀门腐蚀、老化、破损和工作人员操作不当等原因均可使阀门的密封面遭到破坏,从而发生阀门泄漏的现象,其中阀门内漏因为现象不明显,比外漏情况更难以检测。阀门内漏不仅造成资源浪费,还常伴随着经济损失,甚至人员伤亡。过去针对阀门检修的方法主要是进行定期检修,将所有阀门拆卸、检查、修复。这种方式缺乏针对性,不仅导致大量的人力物力浪费,还非常费时,造成大量的经济损失。目前用于阀门内漏检测的技术有压降法、热红外法、超声检测法和声发射检测法等。这些检测技术中,声发射检测法因其低成本、非侵入式测量的优点,被广泛应用于阀门故障检测[1]。

通过分析声发射传感器采集的阀门内漏声发射信号,提取与阀门泄漏率最相关的特征量,可以预估阀门内漏率,极大地减少阀门内漏引起的安全事故。国内外对于阀门泄漏率的定量研究大多也都是基于上述原理。如戴光,等[2]对闸阀的内漏过程进行了理论分析建模,研究了压差与泄漏率、压差与振幅、振幅与泄漏率之间的关系。Lee,等[3]通过分析内漏阀门产生的声发射信号的时频特征后发现,内漏声信号的均方根值与压差和泄漏率相关,特征频率与故障模式相关。Ye,等[4]利用高斯回归过程建立多元数学模型,用于描述声发射信号的特性与压力、泄漏率之间的关系。宗福兴,等[5]采用互相关结合小波变换的方法实现了对原始信号的去噪,改善了内漏率估计精度。Abiodun,等[6]利用声发射信号的6个时域特征参数作为输入,训练神经网络模型,成功实现阀门内部泄漏的评估。Sim,等[7]评估了声发射技术在往复压缩机阀门泄漏检测中的潜力,根据均方根值拟合泄漏量的经验公式。赵翰学,等[8]通过小波分解增加样本数量,建立BP神经网络模型,实现了对阀门内漏速率的量化预测。上述方法虽然可以在一定程度上预判阀门内漏率,但普遍误差较大,而且主要的研究对象是实验室的小孔径阀门,难以模拟真实的炼化生产环境下阀门出现内漏的情况。

针对现有研究对于阀门内漏率预判误差较大,且因缺少炼化实验用的阀门难以模拟炼化生产常用阀门出现内漏的情况,本文着重对炼化生产中常用的孔径为50 mm的闸阀是否发生内漏的情况进行判别研究。实验部分基于户外大型实验场地,通过控制不同的闸阀开度,采集不同开度下的阀门内漏声发射信号,模拟闸阀因密封面遭破坏导致阀门内漏的情况。为了分析阀门内漏声信号的本质特征,提高信号的信噪比和判别准确率,采用变分模态分解和支持向量机相结合的方式对内漏信号进行去噪和分类,最终将阀门内漏识别准确率提高至95.5%。

1 闸阀内漏声场数值模拟研究

1.1 阀门内漏声信号产生机理

当闸阀发生内漏时,在闸板前后高压差动力推动下,流体介质通过内漏孔或内漏缝喷射形成不规则的高速湍流,同时产生喷流噪声,张颖[9]指出这种动态流体声源受固体边界、流体状态及流体间相互作用等因素的影响,声源主要包括喷流噪声、阻塞喷流噪声和涡流噪声3种,有效声源主要是由于流体达到喷流状态引起的空气动力声。

为探究阀门内流体介质压力和流速的关系,利用Fluent软件对阀门进行流场仿真。首先对闸阀的流道进行简化,将闸阀的模型和管道的模型简化为一个闸板和管道相结合的结构,稳态模型选择k-e模型,瞬态模型选择大涡流模型。闸阀的闸板打开非常小的缝隙来模拟闸阀密封面破损的情况,阀门管道流体仿真几何模型、闸阀盘附近流体速度矢量图、闸阀板附近的流体压力分布图见图1。从图1中可以发现在闸板未关紧的地方,闸阀内流体介质的压力越来越小,压力的变化主要集中在闸板未关紧的地方,闸阀板左边区域压力明显高于右边区域压力。通过对比闸阀盘附近流体速度矢量图和闸阀板附近的流体压力分布图,还可以发现流体速度大的区域,压力小;流体压力大的区域,速度小。

数值计算后,需要对计算结果进行后处理,即对结果进行可视化展示,提取闸阀管道的压力云图和速度流线图等,便于对闸阀管道在不同工况下的流场情况进行对比分析。以DN100闸阀、开度20%、上下游压差为1 MPa、介质为空气的稳态仿真结果图为例,图2是闸阀仿真图和闸阀仿真局部放大图,由图2(b)红色方框标记处可知,流体经过闸板后,在下游靠近闸板处会产生大的涡旋,这会形成涡流噪声,与阀门内漏噪声类型相对应,可看出压力大的区域速度小,压力小的区域速度大。

图2 闸阀稳态仿真局部放大图

图3是涡量图,该涡量图采用的是Q准则下的涡量。由图3可知,流体在流过闸板后会形成涡量,即在经过闸板后的一段区域内会有一定的涡量延伸。而介质在流入管道和流过闸板一段距离后是没有涡量出现的。

图3 涡量图

1.2 不同上下游压差情况下闸阀声场数值模拟分析

闸阀开度为20%,上下游压差分别为0.5,1.0,1.5,2.0,2.5,3.0 MPa,控制下游压力保持0不变,改变上游压力的大小。图4为保持闸阀开度不变、不同压差下闸阀管道的压力云图,可知,在保持其他条件不变只改变闸阀上下游压差的情况下,管道闸阀内的压力分布不变,改变的只是在管道和闸阀内相同地方的压力值。统计6个压差下的最低压强值可得最低压强随压差的变化如图5所示,可知在闸阀开度一定的情况下,闸板附近的最低压强随上下游压差的增大而减小。

图4 闸阀不同压差下压力云图

图5 最低压强和压差的关系

压力云图能够得到管道阀门内的压力分布情况,速度流线图能够得到速度分布情况和大小情况。图6为保持闸阀开度不变,改变上下游压差的各个压差下的速度流线图。由图6可知,在闸板底部有明显的喷流现象,速度也在该处急剧增大,这会产生喷流噪声,在下游靠近闸板处形成旋涡,这会产生涡流噪声。图7为最大速度随压差的变化图,由图可知在闸阀管道开度一定的情况下,管内最大速度随压差的增大而增大。由图6可知,不同上下游压差下,速度流线图的分布是几乎不变的。

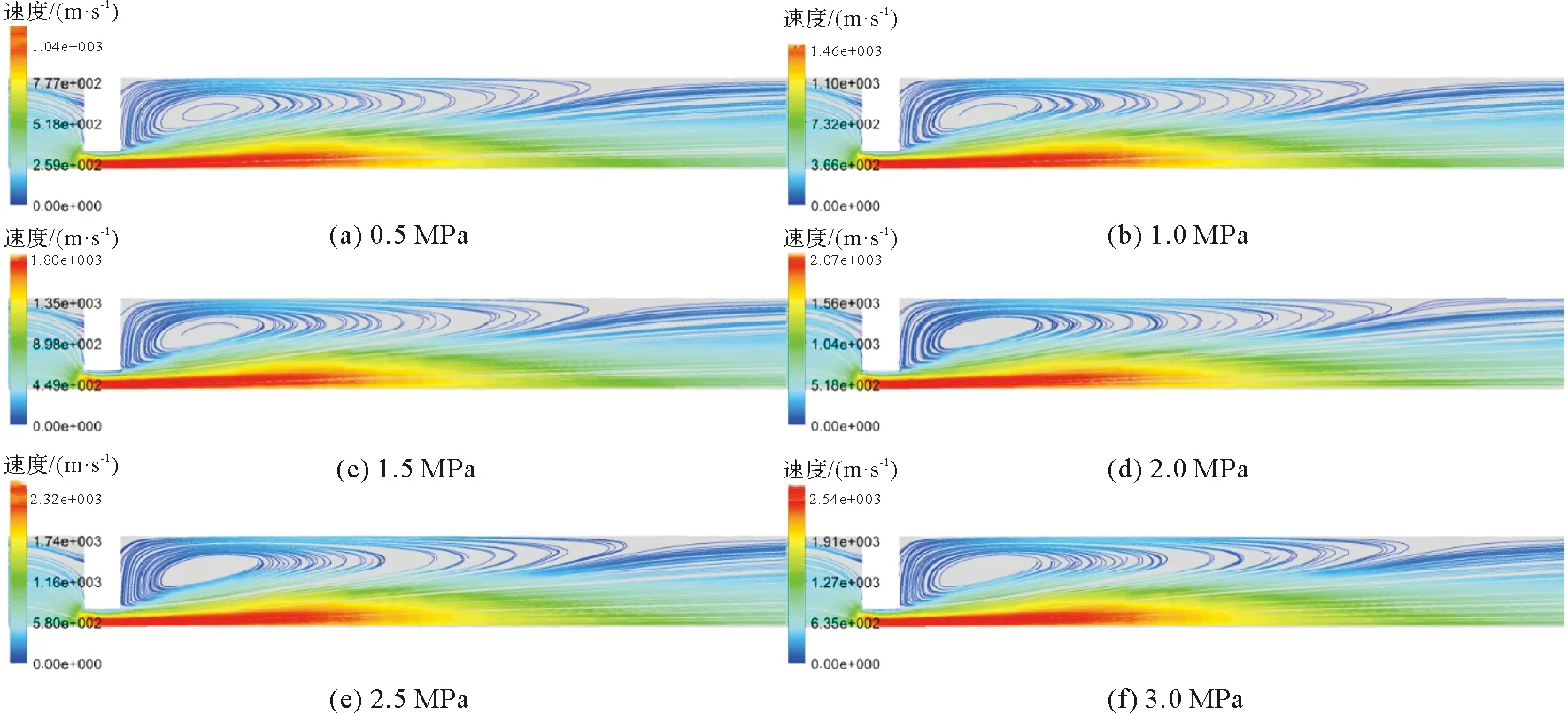
图6 闸阀不同压差下速度流线图

图7 最大速度和压差的关系

1.3 不同开度下闸阀声场数值模拟分析

在保持上下游压差为1 MPa的情况下,研究在不同开度下流场的压力和速度分布及大小变化。本组实验一共仿真4个闸阀开度:5%,10%,20%,30%。图8为4个开度的压力云图,在上下游压差不变,改变闸阀的开度的情况下,会影响闸阀管道内的压力分布,这和不同压力下的压力云图结果是不同的。图9为闸阀管道不同开度下的速度流线图,不同开度下流体的分布及流速大小是不一样的。开度越小,流体经过闸板缝隙之后在下游形成的涡旋就越大,开度越大时涡旋越小,喷流的速度越大。图10为保持压差不变,管道内最低压强随开度的变化图,由图可知,最低压强随开度的增大而减小。

图9 闸阀不同开度下速度流线

图10 最低压强和阀门开度的关系

图11为保持压差不变,管道内最大速度随开度的变化图,由图可知,最大速度随闸阀开度的增大而增大。

图11 最大速度和阀门开度的关系

2 算法理论

结合炼化现场噪声特性及阀门内漏声信号特性,本文提出结合变分模态分解(Variational Mode Decomposition,VMD)和互信息熵来抑制噪声,提取时频和统计特征,最后通过支持向量机进行内漏识别的方法。

2.1 变分模态分解原理

经验模态分解(Empirical Mode Decomposition,EMD)作为一种近年来比较流行的处理非平稳信号的方法,其分解过程是将包含噪声的时域信号自适应的分解到多个经验模态中,利用某些特征选择方法选取主要的经验模态,重构有效的源信号[10-11]。但是EMD不仅缺乏严谨的数学解析过程,其分解过程甚至会出现模态混叠以及端点效应[12]。Dragomiretskiy,等[13]在2014年时提出了一种基于EMD的新的信号分解方法,即变分模态分解(VMD),它能够识别出信号的奇异性,并且分解的特征模态稳定性较好,VMD能够将所有的本征模态函数的中心频率以及带宽确定下来[14]。另外与EMD相比,VMD有着扎实的理论并且在抑噪方面具有更出色的鲁棒性。

使用VMD方法之前,需要进行变分问题的构造,其实质是将信号分解为多个模态函数。用f表示信号,uk(t)代表模态函数,k来代表预设分解的个数。估算带宽的步骤如下:①分析求解uk(t)的解析信号,将单边频谱求解出来;②用e-jωkt来表示混合预估中心的频率,将全部模态的频谱转换到对应的基频带中[15];③II2来表示信号的梯度的平方范数,如果信号被分解为k个本征模态函数IMF分量,其相应的约束变分模型计算公式为:

(1)

式中:δ(t)——单位冲击信号;

wk——中心频率;

j——虚数符号;

t——时间。

以上便是VMD的频带宽估计过程,在实际使用中,VMD根据预设分解尺度k,将实际信号分解成k个有效模态[16]。

2.2 支持向量机(SVM)原理

SVM技术针对小样本数据和非线性分类具有较好的分类效果,其分类理论是建立在统计学习和结构风险最小原理基础之上,能根据样本自身的复杂性和统计信息在分类学习能力之间寻求最佳平衡度[17]。应用SVM分类技术,首要步骤就是建立分类超平面模型:

(2)

式中:x——分类样本点;

w——分类矩阵;

a、b——超参数;

T——转置标志;

y——标签值,取值-1或1。

最优分类超平面尽可能远离所有样本数据点,能对样本间的最优分类界限,SVM的学习过程就是寻找一个最优的分类超平面的过程[18]。假设样本数据中任意一点x到超平面(w,b)的距离为:

r=(wT/‖w‖)·x=|wTx+b|/‖w‖

(3)

定义支持向量点:满足|wTx+b|=1成立的样本点为支持向量点,即支持向量位于间隔边界处。为了寻找最优超平面(最优分类间隔),还需要定义目标函数:

max(2/‖w‖)

(4)

s.t.yi(wTxi+b)≥1

s.t.(·)是目标函数的约束条件,为了使目标函数优化过程更可靠稳定,可将式(4)的最大化过程转化为:

max(‖w‖2/2)

(5)

s.t.yi(wTxi+b)≥1

利用拉格朗日乘子可以得到目标函数式(5)的对偶问题:

(6)

令L(w,b,α)对w,b的偏导数为零:

(7)

式中αi为拉格朗日乘子,对于任意训练样本数据点,总存在αi=0,等效于最终与分类模型有关的样本点都位于最大间隔的边界上,即上述支持向量点,其余样本点与分类模型无关[19]。

2.3 互信息熵

互信息熵可以量化两个随机变量之间的依赖关系,本文利用互信息熵分析原信号和经过VMD分解后的子信号之间的相关性。对声传感器采集的泄漏声信号x进行分析,x经VMD自适应分解成若干个子信号。为进一步度量分解子信号vi所包含的泄漏有效成分,分别计算子信号vi与泄漏声信号x之间的互信息熵:

I(x;vi)=∑∑p(x;vi)log[p(x;vi)/p(x)p(vi)],
i=1,2,3,4,5

(8)

式中:p()——概率密度;

I(x;vi)——分解子信号vi同泄漏声信号x的互信息熵。

3 实验研究

3.1 泄漏信号数据采集

搭建了模拟炼化装置阀门内漏的实验装置,如图12所示,由闸阀、声发射传感器、NI多通道数据采集卡、计算机、空气压缩机和气体流量计组成。其中实验阀门的孔径为50 mm,材质为不锈钢,声发射传感器安装在阀门附近的上下游管道上,采集卡的采样率设置为1 MHz,单次采集时间为10 s,共采集泄漏声信号(闸阀开度50%)200组,无泄漏声信号(背景噪声)200组。

图12 阀门内漏检测数据采集实验装置现场

在多数现场生产情况下,50%以上阀门内漏可由巡检人员人耳识别,本文选用关闭到50%开度区间内的实验作为分析数据,认为50%开度是泄漏声信号能量最小的起始度量,其对泄漏识别的作用具有较大意义。为验证不同开度对声信号的影响,比较分析了闸阀DN50在0.6 MPa气体介质时,不同开度下的信号时域图,如图13所示,随着开度变大,信号能量值变大,但是50%开度对应的泄漏声信号能量是最小的,分析是由于50%开度下,阀体对管内流体的阻滞作用最弱,流体激发出的声振动波也就最弱。

图13 不同开度条件下的信号时域

3.2 泄漏信号去噪预处理

本文选取位于阀门下游的声传感器1采集的泄漏声源信号x进行分析,声信号经VMD自适应分解后得到5个子信号,信号时域形式如图14所示。可以发现子信号v1、v2、v3、v4的时域波形同原始信号比较相似,而v5的时域波形与x有较大差异,因此可初步认为v1、v2、v3、v4含有的泄漏信号有效成分高于v5。图15是据式(8)计算的互信息熵值绘制而成的分布直方图,可以看到子信号v5与泄漏声源信号x之间的互信息熵最小,表明v5与原信号的相关性最小,因此可以将v5分量剔除,利用剩下的v1、v2、v3、v4重构原信号。重构后的信号x1和原始信号x如图16所示,从两者的波形对比中可以发现,信号x1因为滤除了噪声,幅值大幅度减少,但基本特征与原始信号x一致,实现了滤除噪声而保留原始信号特征的目的。利用同样的处理方式对其它信号进行降噪预处理,得到一系列重构信号。

图14 泄漏声源信号x与分解信号v1～v5时域形式

图15 泄漏声源信号x与分解信号v1～v5的互信息熵

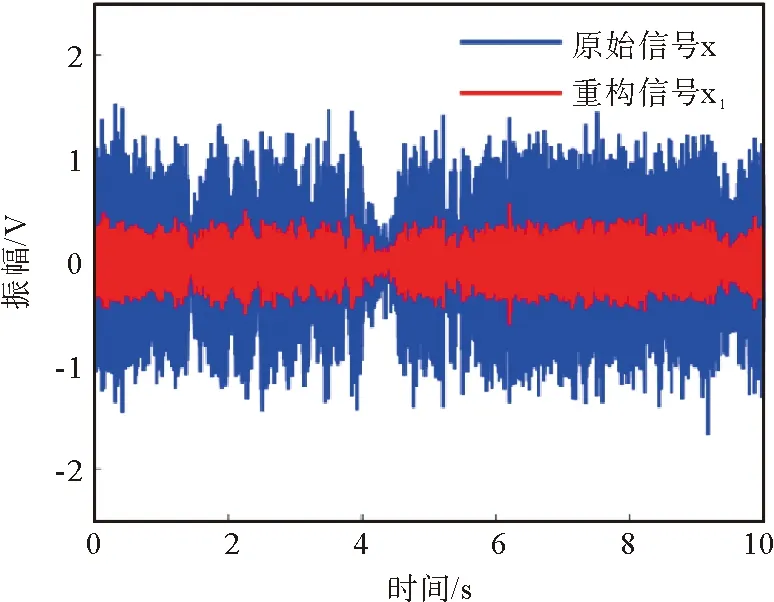
图16 泄漏声源信号x与重构泄漏声信号x1

3.3 泄漏样本特征提取

选择均方根(Root Mean Rquare,RMS)、梅尔倒谱系数(Mel Frequency Cepstral Coefficients,MFCC)两种声发射特征值统计特征量绘制样本的散点图,并以此图论述本文算法性能[20]。如图17(a)为信号经EMD降噪预处理后,提取的RMS和MFCC统计特征散点图,绿色圆点是无泄漏样本点,黑色圆点是泄漏样本点,可以发现图中(红色椭圆内)两类样本之间存在多个交叉样本点,没有明显的分界线,对于微小泄漏的情况,算法的识别效果较差;图17(b)为信号经VMD降噪预处理后,提取的RMS和MFCC统计特征散点图,可以发现(红色弧线),两类样本的界限十分明显,表示此分类方法效果较好,可以实现对微小内漏的判别。

图17 样本散点图

3.4 泄漏状态识别

将EMD去噪处理后提取的特征量作为本算法的对比案例,在分类识别过程中,采用10折交叉验证方法验证算法的性能,如图18所示分别为EMD-Nonlinear SVM和VMD-Nonlinear SVM对数据集样本的分类识别结果(○为支持向量样本点)。图中包含2种不同的色块,即橙色块和蓝色块,2种色块对应2种类别的样本,可以看到2类色块分类界限较为清晰,但单纯的色块分布情况还不足以说明所提出的算法流程的优越性。

为进一步分析对比EMD-Nonlinear SVM与VMD-Nonlinear SVM的分类识别性能,引入混淆矩阵这个评价指标。混淆矩阵多用于判断分类器的优劣,其一级指标如图19所示,其中TP表示真正正样本,FP表示假正负样本 ,FN表示假负正样本,TN表示真负负样本,在本文中未泄漏表示正样本,泄漏表示负样本。

图19 混淆矩阵的一级指标

由图19的一级指标可以计算出模型的分类精度(Accuracy)二级指标:

(9)

图20为EMD-Nonlinear SVM与VMD-Nonlinear SVM的分类识别结果,据式(9)的定义和实际统计结果,EMD-Nonlinear SVM的分类精度为86.0%,VMD-Nonlinear SVM的分类精度为95.5%,因此VMD-Nonlinear SVM的分类精度要高于EMD-Nonlinear SVM。为全面对比所提出的VMD-Nonlinear SVM算法流程的分类识别性能,引入Nonlinear SVM对泄漏样本数据进行分类,从图20可以看到,分类结果与实验次数无关,在3个分类算法中,VMD-Nonlinear SVM的分类精度始终最高,EMD-Nonlinear SVM分类精度次之,而Nonlinear SVM的分类精度最差。

图20 3种算法流程对阀门泄漏数据样本的分类精度

炼化现场因生产活动,背景噪声成分比较复杂,但针对这些噪声成分,均可使用本文所提出的信号提取处理技术进行滤噪操作。表1是不同噪声源存在下的分类识别实验结果,从数值可以看到,在阀门关闭和有开度的情况下,实验仍然选用本文的RMS和MFCC特征参数。在不同的噪声背景下,EMD-Nonlinear SVM方法分类精度较低,通过本文的滤噪处理,本文提出的VMD-Nonlinear SVM方法分类精度有明显的提升,这意味着提高了对阀门泄漏识别的准确度。

表1 不同噪声源、阀门开度下两种方法的分类精度 %

4 结语

鉴于现有研究对泄漏率的预估误差较大且实验条件过于理想,不能模拟真实炼化现场的情况,本文利用声发射检测技术研究炼化行业阀门内漏信号去噪识别技术,采用VMD方法对泄漏噪声信号进行分解和降噪,以互信息熵为判断依据,剔除互信息熵较小的分解子信号,重构泄漏声源信号。为绘制可视化图形,提高方法的可操作性,采用了梅尔倒谱(MFCC)和均方根(RMS)这两个特征参数。从判别结果可以看出,与现有同类型的Nonlinear SVM、EMD-Nonlinear SVM分解技术对比,本文提出的VMD-Nonlinear SVM方法经过多次实验,始终具有最高的分类识别精度,对现场复杂环境下的阀门内漏信号识别效果最好。