连续油管防喷器闸板剪切钻杆过程的力学性能

刘 冰 李 涛 赵永杰 陈金钢 周婷婷 綦耀光

1.山东科技大学机械电子工程学院 2.中国石油大学（华东）机电工程学院

0 引言

陆上油气钻采领域发生的井喷/井涌事故中，一个重要原因是使用的防喷器没有安装剪切闸板或剪切闸板未能及时切断作业管柱[1-3]，虽然剪切闸板在作业中极少使用，但对于需要切断作业管柱才能实现安全封井的危急情况却是必不可少的[4-5]。因此，研究剪切钻杆过程中的剪切闸板力学性能对于确保油气钻采安全具有重要意义。目前，国内外学者对剪切闸板的剪切性能做了大量的研究工作。Childs等[6-7]以畸变能理论为基础结合回归分析法建立闸板剪切力预测式。Springgett等[8-9]在剪切力计算式的基础上，研究V形剪切闸板在V形剪切技术中的应用。俄亥俄州立大学的研究人员综合考虑管内流体等因素数值模拟剪切闸板的剪切过程得到闸板带压作业的剪切力[10-11]。Koutsolelos等[12-13]运用改进摩尔—库伦准则结合有限元分析求解剪切闸板的剪切力。赵维清等[14-16]通过数值模拟研究剪切闸板的剪切性能，王鹏程等[17-18]则提出利用机器视觉技术和图像处理技术建立剪切闸板的量化评价方法。

虽然上述研究对于确保油气钻采安全作业有着重要的意义，但却多集中于剪切闸板的剪切能力，而对剪切过程中闸板自身的力学性能则鲜有涉及。虽然运用实验或数值模拟的方法可以获得剪切钻杆过程中剪切闸板的应力应变特性[19-20]，但往往只针对特定的剪切作业且未进行理论分析，不具有普适性。基于此，笔者根据剪切闸板基本运动规律，按照剪切点接触、切入及穿透钻杆3个阶段，运用楔形体应力理论，综合考虑剪切闸板结构参数及作业参数，分别求出相应阶段闸板刃口应力函数，结合数值模拟和剪切试验研究剪切过程中的闸板力学性能。

1 剪切钻杆过程中的力学分析

剪切闸板在液压系统提供的推力作用下向位于防喷器中心的钻杆运动，第一阶段剪切闸板靠近并接触钻杆；第二阶段闸板刃口挤压钻杆，使钻杆屈服，在刃口接触区出现明显的颈缩现象，楔形刃尖锥入钻杆；第三阶段钻杆断裂破坏，楔形刃尖进入钻杆环空区，最终完成对钻杆的剪切。剪切闸板楔形刃尖接触钻杆时的状态，如图1所示。

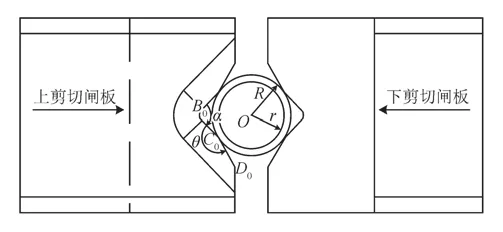
图1 上下剪切闸板剪切钻杆示意图

根据闸板剪切运动过程分析，可将剪切闸板作用力分为剪切点接触钻杆、切入钻杆及穿透钻杆壁厚进入钻杆环空区3个阶段。

剪切闸板楔形刃尖（剪切点）接触钻杆时，在液压驱动系统作用于闸板背部的驱动力下，在接触点处，对钻杆仅有正向作用力（F0），如图2-a所示。当剪切闸板切入钻杆时，按照其作用性质可分为实现压裂钻杆正前方的正向作用力及挤压钻杆的切向作用力。切向作用力包括由楔形刃尖角的两个楔形边及刃口厚度所在平面产生的两个挤压力F01及F02，由刃面倾角所形成的斜截面在两楔形边处的挤压力Fj1和Fj2，如图2-b所示。剪切点进入钻杆环空区时，闸板剪切钻杆的力与切入钻杆时相似，所不同的是其刃口与钻杆的接触位置不同，即力的作用部位不同，如图2-c所示，此不赘述。

2 剪切闸板的应力分析

2.1 剪切点接触钻杆时的闸板应力

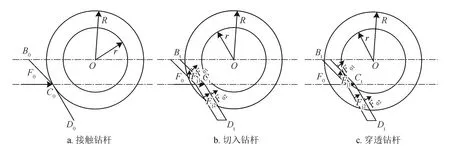
图2 剪切闸板不同阶段对钻杆的作用力图

剪切闸板剪切点初次接触钻杆时，在钻杆接触区，对钻杆仅有正向作用力F0。此时，可近似认为剪切闸板楔形刃尖承受集中载荷F0'：

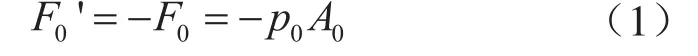
式中p0表示液压系统作用于剪切闸板背部的驱动力，A0表示剪切闸板背部的承压区。

如图3-a所示，其中剪切闸板的楔形顶角为θ，刃口厚度为h。

根据本文参考文献[21]及密切尔解答，有

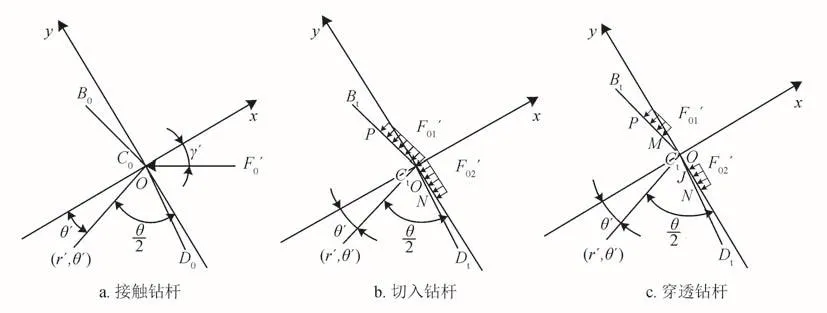
图3 闸板剪切钻杆时的刃口应力图

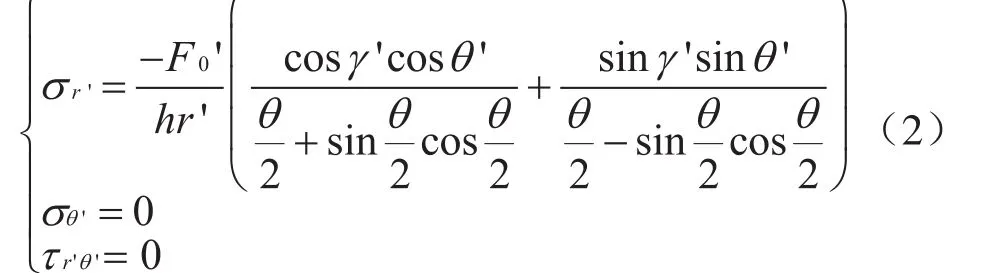
式中σr'表示剪切点的径向应力；γ'表示集中载荷与x轴的夹角 ；σθ'表示剪切点的切向应力 ；τr'θ'表示剪切点剪应力；(r', θ')表示直角坐标系x'C0y'对应的极坐标系。式（2）可表示为

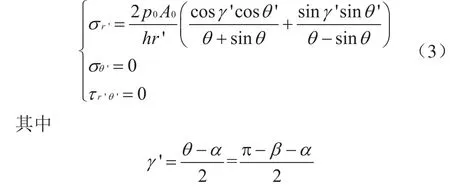
式中α表示剪切闸板V形角；β表示刃口倒角。

由式（3）可知，当r'→0时，σr'→∞，说明在载荷F'的作用点处的应力无穷大，即解答不适用。根据闸板剪切钻杆的实际情况，剪切点在接触钻杆外径的一瞬间，外力不是作用在剪切点这一单点上，而是由闸板刃口厚度所确定的微小区域上，说明此时在闸板刃口处出现应力集中现象。

2.2 剪切点切入钻杆时的闸板应力

根据闸板的剪切运动，设在t时刻，剪切闸板（以剪切点C为参考）运动至Ct，此时剪切闸板在Oxy面的投影如图3-b所示。假设剪切闸板对钻杆的压应力满足连续均匀分布，即在剪切闸板楔形边LPCt、LNCt分别作用有均布载荷和且

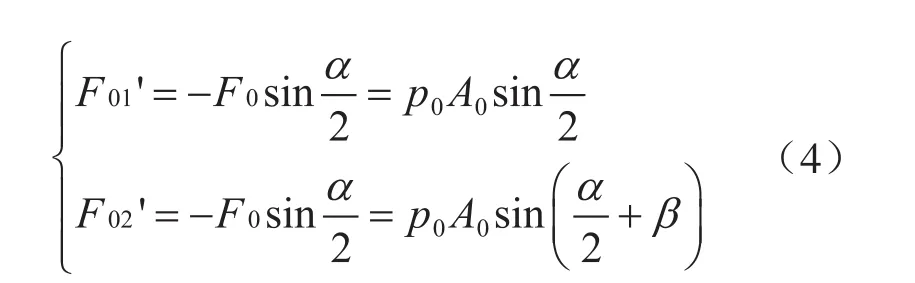
根据本文参考文献[22]所述的对称楔形体在楔面受一段均布力作用的弹性应力解，可得楔面PCt上的弹性应力函数：

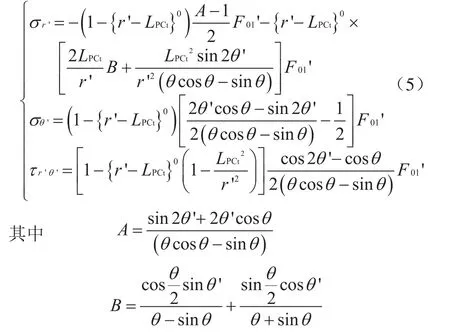
同理可得在楔面NCt上的弹性应力函数为：

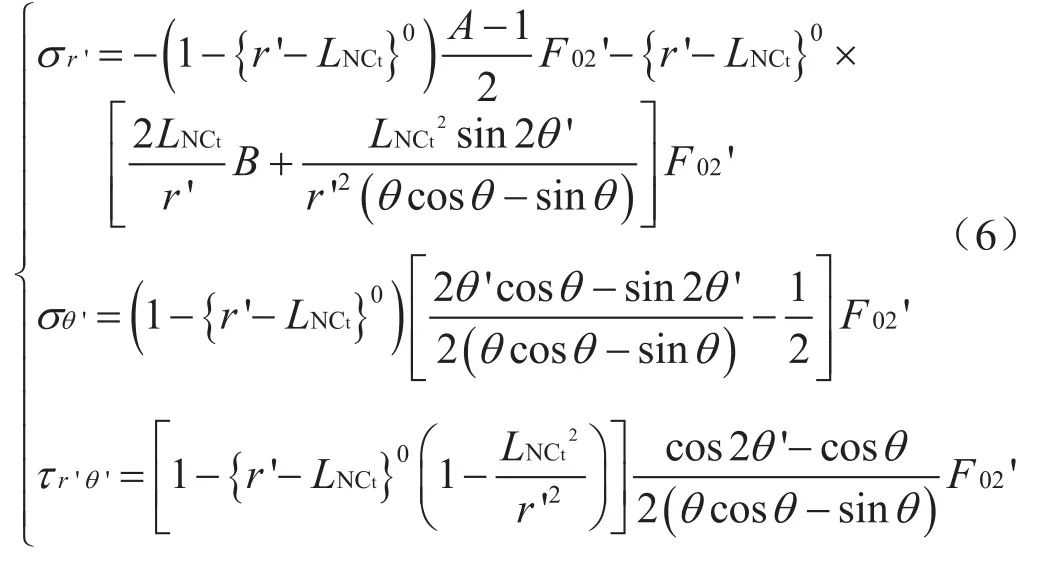
由式（5）和（6），根据叠加原理可得剪切闸板压入钻杆的弹性应力函数为：

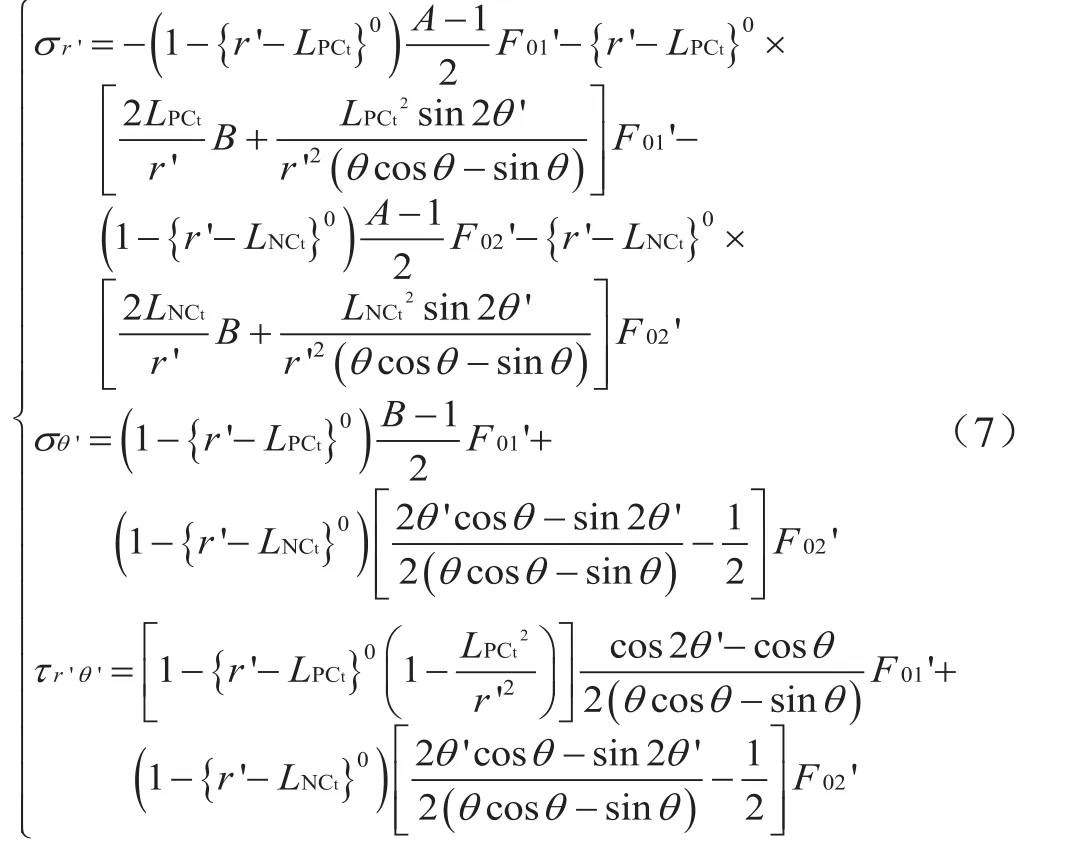
2.3 剪切点进入钻杆环空区时的闸板应力

当剪切点进入钻杆环空区时，闸板应力如图3-c所示，同理可求得楔面MCt上的弹性应力函数，根据叠加原理可得PM和JN段的弹性应力函数式：

由式（8）和（9），进而得到剪切点进入钻杆环空区的弹性应力函数：

式中a泛指长度单位。

3 剪切钻杆过程的数值模拟

3.1 数值计算模型

以某型号连续油管（以下简称CT管）防喷器的剪切闸板和CT90连续油管为基础建立闸板剪切的数值计算模型。为便于分析，将剪切闸板本体及冲击块简化为一体式的并忽略非关键部位的圆角、倒角等，定义剪切闸板为刚性体，材料塑性特征采用刚塑性模型，屈服强度为960 MPa、塑性应变为0；抗拉强度为1 050 MPa，塑性应变为0.15。用C3D4四面体单元对剪切闸板进行整体网格自动划分，刃口网格细化，上、下剪切闸板单元数各47 801个。钻杆采用的CT90管为弹塑性体，长400 mm，塑性参数采用Johnson-Cook材料本构模型：初始屈服应力为621 MPa、应变强化系数为680 MPa、应变速率强化系数为0.01、温度软化指数为0、应变强化指数为0.25；断裂破坏参数采用Shear Damage模型，断裂应变为0.2、等效失效应变（失效位移）为1，CT90管网格类型为C3D8R六面体单元，对剪切段网格细化，单元总数3 024个。剪切闸板及CT90管材料特性参数如表1所示。

约束CT管上端面z方向移动，模拟油管上端的悬挂状态，CT管下端面加载井内油管的自重载荷及重力。剪切闸板在防喷器壳体腔内只能在x方向上来回移动，故在闸板顶部后表面的y、z方向移动及3个方向的转动自由度施加约束。在闸板背部施加的液压驱动力以20 mm/s的速度载荷表示。数值分析模型如图4所示。

表1 剪切闸板及CT90管性能参数

图4 剪切CT90管数值计算模型图

3.2 模型结果分析

基于ABAQUS有限元分析软件得到闸板剪切运动至钻杆不同位置时的应力云图如图5所示（上下剪切闸板相同和剪切运动的对称性，故此处以上剪切闸板表示）。

由图5可知，剪切闸板靠近钻杆过程中，剪切点未接触CT90管时，闸板V形角中心区应力最大，应力值为492.6 MPa（图5-a），该应力是由速度载荷产生的。随着剪切继续进行，闸板最大应力区逐渐向V形角两侧扩展，剪切点接触CT90管时，应力峰值迅速转移至刃口剪切点的极小区域内，且应力值陡增至1 016 MPa（图5-b），超过剪切闸板屈服强度，即闸板刃口出现应力集中现象，这与闸板应力的理论分析表现一致。

当剪切点切入CT90管时，闸板最大应力出现在剪切点及其楔形边两侧，应力值高达1 050 MPa（图5-c），达到剪切闸板的强度极限，这是由此时闸板刃口受到的闸板速度载荷、CT90管的材料强度及其对闸板刃口的反作用力共同作用所致。

当剪切点进入CT90管环空区时，闸板最大应力出现在刃口倒角与垂直面的交界两侧，说明此交界处已接触CT90管，而由于刃口倒角在此交界处形成一个新的楔形尖，根据前述分析可知，此处也发生了应力集中，故应力值高达1 027 MPa（图5-d）。设计剪切闸板时，刃口倒角位置应偏向远离V形角一侧，以避免非关键剪切部位出现应力集中现象降低剪切闸板性能。

4 剪切过程中的闸板应力实测

4.1 测试装置及材料

试验采用的测试装置如图6所示，试验装置主要由连续油管闸板防喷器（共4组闸板，其中从上往下第二组为剪切闸板）、CT90管、压电传感器、电荷放大器、数据采集卡、管路系统和计算机及数据处理系统组成。其中，压电传感器采用PZT4薄片，置于剪切闸板楔形刃尖后方的凹槽内，电荷放大器为BZ2104型的6通道电荷放大器，数据采集卡为USB-6211型数据采集卡，计算机及数据处理系统能够实时地将采集到的电荷信息转换为应力存储并输出。

4.2 测试方案

图5 剪切过程中上剪切闸板的应力云图

图6 剪切过程中的闸板应力测试系统图

将闸板防喷器安装固定在地上的凹坑内（试验井口）上，连接防喷器开启管线和关闭管线，剪切闸板的楔形刃尖后部开有微小凹槽用以放置与数据采集系统相连的压电传感器，将CT90管垂直悬挂于防喷器上方，然后放入井眼内。在闸板背部施加10.5 MPa的关井压力，按照规定的关井要求，完成剪切钻杆的封井操作，计算机及数据处理系统根据压电传感器测得的电荷量，即可得到并输出剪切过程中闸板刃口剪切点的应力数据。

4.3 测试结果分析

图7是根据CT管防喷器的某新型剪切闸板数值模拟剪切CT90管和剪切试验获得的上剪切闸板刃口剪切点应力数据绘制的曲线。

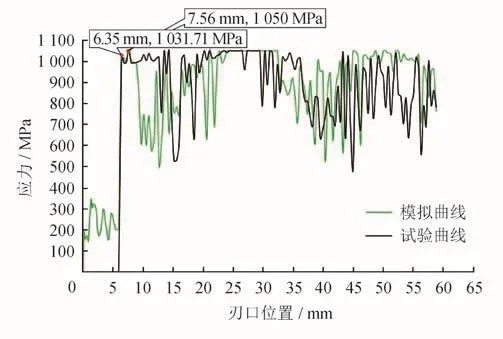
图7 剪切闸板刃口剪切点应力变化曲线图

由剪切闸板剪切点应力曲线。可以看出：

1）剪切点未接触钻杆时，剪切试验的剪切点应力几乎为零而数值模拟的剪切点应力较小，这是由于剪切试验是在闸板背部施加10.5 MPa的均布载荷，传递至闸板前部时几乎可以忽略，而数值模拟是在整个闸板上施加的速度载荷来代替封井力，故剪切点的应力是由速度载荷产生的。

2）剪切点接触CT90管的瞬间剪切点应力陡增至1 031.71 MPa，逼近闸板强度极限，与数值模拟结果（陡增至1 016 MPa）表现出高度的一致性，即剪切点处出现应力集中现象。随着剪切进行，剪切点切入CT90管，剪切点应力略有降低，这是由于剪切点接触区增大，应力逐步分散，后在背部压力和CT90管材料强度的作用下又增至闸板强度极限1050 MPa，工作短时间后，CT90管达到断裂极限开始断裂，剪切点进入CT90管环空区，应力再次回落，随后由于材料的加工硬化剪切点应力出现多次波动。

3）此外，可以发现在剪切段（6.35～13.55 mm），剪切点应力模拟曲线比试验曲线下降更快，幅度更大，且在整个剪切过程中试验曲线波动频率相比于模拟结果要高但波动幅度较小，这是因为在试验条件下闸板刃口要受到摩擦力及其他因素影响。

图8是剪断CT90管后的剪切闸板刃口情况，可以看出刃口剪切点所在的区域出现裂纹崩刃现象，这是由于剪切点在开始剪切CT90管时出现应力集中，后又在达到闸板刃口强度极限的情况下剪切工作一段时间所致。

图8 剪断CT90管后的剪切闸板刃口图

5 结论

1）根据剪切机理将剪切过程分为剪切点接触、切入及切透钻杆壁厚进入钻杆环空区3个状态，分析相应状态的闸板作用力，基于楔形体应力理论求解得到闸板刃口应力函数。

2）剪切点接触CT90管时，闸板刃口剪切点附近区域出现应力集中现象；剪切点切入CT90管时，闸板最大应力出现在剪切点及其楔形边两侧，应力值达到剪切闸板的强度极限1 050 MPa；剪切点进入CT90管环空区时，闸板最大应力出现在远离剪切点的楔形边和刃口倒角与垂直面的交界两侧，与各阶段闸板应力的理论分析表现出一致性。

3）设计剪切过程中闸板应力的测试试验，获得剪切CT90管过程中的剪切点应力变化规律，与数值模拟结果吻合，剪断CT90管后的闸板刃口剪切点附近区域出现裂纹损伤。

运用楔形体应力理论，建立各阶段的闸板刃口应力求解模型，能够较好地反映出剪切过程中闸板刃口的应力状态及其与钻杆之间的相互作用，可为设计制造与现场正确使用提供重要的参考依据；但由于应力函数模型存在较多参数且部分参数难于确定，使得准确求解各阶段的应力值较为困难，因此有必要研究其中部分参数的求解方法，以期能够更好地反映剪切闸板的力学性能。