单节热离子燃料元件燃料质量迁移及其对元件性能影响

雷华桢,钟武烨,姜 玮,赵振华

(1.中国原子能科学研究院,北京 102413;2.中核战略规划研究总院,北京 100048)

单节热离子燃料元件(TFE)能够实现静态热电转换,且结构紧凑、欧姆损耗小、输出电压大,具有明显的技术优势和广阔的应用前景。根据理论分析,热离子转换的热电转换效率最高可达35%,实验室中热离子转换的最高热电转换效率目前已可达到25%,而目前工程中仅能达到理论值的30%～40%[1]。为实现热离子转换,单节热离子燃料元件运行温度远高于压水堆燃料元件。高温下燃料芯块与发射极接触产生较强的机械相互作用,使发射极产生蠕变,可能导致发射极与接收极接触造成短路,威胁单节热离子燃料元件的正常运行。

国内外针对单节热离子燃料元件行为特性开展了大量研究。俄罗斯及苏联开展了大量电加热和核加热地面实验[2-3],得到了一系列燃料芯块高温蠕变和热离子转换性能数据。在大量的试验数据及设计工作经验支持下,鲁奇研究所开发了单节热离子燃料元件性能分析程序KATET[4],该程序考虑了单节热离子燃料元件的传热、变形和热电转换行为,主要关注燃料芯块和发射极的行为和相互作用,包括燃料质量迁移导致燃料芯块变形、燃料质量迁移对轴向功率分布影响、与燃料芯块接触下发射极变形等,计算得到在稳态运行过程中单节热离子燃料元件温度分布和发射极尺寸的变化。Xue等[5]建立了一维和二维单节热离子燃料元件稳态性能分析模型,开展了热工和热电转换计算,与电加热试验值符合较好。中国原子能科学研究院针对单节热离子燃料元件和热离子反应堆开展了试验和理论研究,包括电极材料、排气装置、源项研究等[6-8],并开展了热离子转换性能试验和堆内辐照变形试验,获得一系列材料局部伏安特性和发射极变形数据。Deng等[9]根据单节热离子燃料元件几何特征对压水堆燃料元件性能分析程序FROBA-ROD进行了改造,对单节热离子燃料元件服役期间的热工机械性能进行分析,发现发射极在高温下蠕变能够释放芯块和发射极的接触压力。沈兰亭等[10]将热离子转换模型与传热模型相结合,对单节热离子燃料元件进行稳态热工性能分析,并对关键参数的计算值与设计值进行了比较分析。

以往研究主要着眼于热离子燃料元件的热工-热电转换性能及材料机械性能,对燃料质量迁移对其影响分析较少。本文基于添加燃料质量迁移模型和热电转换模型的FROBA-KJD程序,通过与试验数据对比进一步验证热工模块后开展单节热离子燃料元件稳态性能分析,研究燃料质量迁移对单节热离子燃料元件各方面性能的影响。

1 数学物理模型

热离子燃料元件的活性区横截面为圆筒状,由多层同心圆环组成,其横截面示意图如图1所示,由内向外依次为燃料芯块、发射极、接收极、接收极绝缘层和内外套管。芯块-发射极间隙内为真空;发射极与接收极之间充入铯蒸气以提高热电转换效率;接收极-内套管间隙内充入氦气以提高换热能力;NaK在内外套管间流动冷却燃料元件。

图1 单节热离子燃料元件活性区横截面

1.1 燃料质量迁移模型

单节热离子燃料元件芯块留有中心孔道以降低芯块最高温度和排放裂变气体。但由于芯块温度仍较高,燃料芯块中心孔道高温区域燃料将蒸发并在低温区域凝结,发生轴向质量迁移,导致燃料芯块中心孔道两端的直径变小,影响裂变气体的排放,并将进一步影响燃料元件内部的压力和温度分布。同时,燃料芯块外表面还将发生径向质量迁移,即芯块外表面燃料蒸发而在发射极内壁面凝结,导致芯块和发射极接触。

1) 轴向质量迁移模型

单节热离子燃料元件中心孔道与外界真空环境联通,且内部分子量极少,质量迁移处于自由分子态,可采用Gontar模型[11-12]进行计算。该模型中假设材料表面分子的蒸发处于平衡状态,蒸发和凝结系数为1。同时中心孔道底部封闭,可认为蒸汽压力等于饱和压力,开放端接近真空,可认为蒸汽压力为0,则中心孔道内不同高度和时间的质量迁移流量为:

(1)

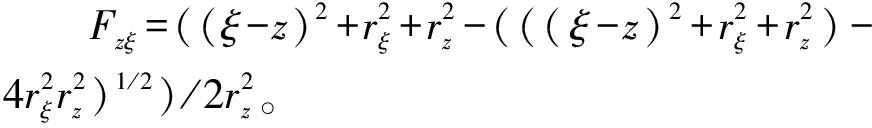
对于单节热离子燃料元件中心孔道,主要考虑UO、UO2和UO3三者的质量迁移,基于化合价守恒、物质量守恒和反应平衡,可以得到U2+、U4+、U6+相对浓度的关系:

(2)

式中:nU2+为U2+的相对浓度;nU4+为U4+的相对浓度;nU6+为U6+的相对浓度;x为燃料芯块氧缺陷。

同时铀离子的反应平衡系数KU为:

(3)

将其代入式(2),即可得到3种铀离子的浓度:

(4)

最后,考虑如式(5)所示各种铀离子和氧的反应平衡,即可得到各种铀氧化物的平衡压力,如式(6)所示。

(5)

(6)

式中:KUO、KUO2、KUO3分别为UO、UO2、UO3的反应平衡常数,由K=exp(A+B/T)计算,A、B为常数,取值列于表1,T为温度,K;pUO、pUO2、pUO3分别为UO、UO2、UO3的饱和压力,atm。

表1 反应平衡常数计算采用的系数[13]

在温度和质量迁移影响下,燃料芯块的氧铀比分布将发生改变。本文采用的燃料芯块为亚化学计量比的二氧化铀,因此用UO2-x表示。其中,氧缺陷可由式(7)[11]计算:

x(z,r)=Cexp[-Q*/RT(z,r)]

(7)

式中:x(z,r)为燃料芯块在(z,r)处氧缺陷;Q*为换热常数,取为142 kJ·mol-1;R为理想气体常数,取为8.314 J·mol-1·K-1;C为计算采用系数,由式(8)[12]计算。

(8)

式中,xav为燃料芯块平均氧缺陷,由燃耗和质量迁移质量流量计算,如式(9)[11]所示。

(9)

2) 径向质量迁移模型

与中心孔道内燃料相似,燃料芯块外表面的燃料同样会蒸发。但由于燃料芯块与发射极之间间隙较小,燃料将在发射极内壁面凝结,并在短时间内(10个小时量级)填满芯块-发射极间隙,造成两者接触[13]。利用文献[14]中给出的数据拟合得到燃料芯块表面蒸发速率关于芯块温度的函数,如式(10)所示。

1/vevaporation=109.23×10-6T2-0.04T+48.62/0.025 4

(10)

式中:vevaporation为径向质量迁移速率,mm·h-1;T为燃料芯块表面温度,K。

1.2 热电转换模型

单节热离子燃料元件电路连接如图2所示,发射极和接收极两端有导线连接。运行过程中,发射极接收裂变热发射热电子,电子跨越极间间隙到达接收极并经两端导线经过负载做功,随后经发射极两端导线流入发射极。在发射极内流动过程中,发射极继续发射热电子,从而形成完整的电路循环。基于上述电子流动规律和欧姆定律,建立发射极和接收极的电势分布方程,如式(11)所示。电势分布方程的边界条件如式(12)所示,通过单根元件输出电压求得发射极和接收极两端电势。

图2 单节热离子燃料元件电路连接

(11)

式中:FE为发射极截面积,m2;FC为接收极截面积,m2;ρE为发射极电阻率,Ω·m;ρC为接收极电阻率,Ω·m;φE为发射极电势,V;φC为接收极电势,V;ΠE为发射极外周长,m;j为发射电流密度,A·m-2。

(12)

式中:φC|z=0为接收极底端电势,V;IC1为接收极底端电流,A;RC1为接收极底端导线电阻,Ω;φC|z=L为接收极顶端电势,V;IC2为接收极顶端电流,A;RC2为接收极顶端导线电阻,Ω;φE|z=0为发射极底端电势,V;Uo为单根热离子燃料元件输出电压,V;IE1为发射极底端电流,A;RE1为发射极底端导线电阻,Ω;φE|z=L为发射极顶端电势,V;IE2为发射极顶端电流,A;RE2为发射极顶端导线电阻,Ω。

发射极与接收极两端流入或流出的电流由对发射极和接收极端面到各自等势面的发射电流积分得到,如式(13)所示。

(13)

发射极与接收极之间气隙内部气体为铯蒸气,由于发射极和接收极间存在热离子转换,因此需要改进发射极和接收极间换热模型。对于发射极外表面,需要被带走的热量包括核裂变产生的裂变热和发射极内电流产生的焦耳热,而热量被带走的方式包括铯蒸气传热、辐射换热、热电转换和电子冷却。因此发射极外壁面的换热关系[15]可表示为:

(14)

发射极和接收极之间的铯蒸气传热系数是铯蒸气平均温度、铯蒸气间隙厚度以及铯蒸气压力的函数,如式(15)所示。

(15)

1.3 机械力学模型

针对单节热离子燃料元件各层材料的变形,本文基于轴对称假设对圆柱坐标系下的力学方程采用边界转移法进行求解[16],力学方程如式(16)所示。

(16)

式中:εr、εθ、εz分别为径向应变、周向应变、轴向应变;ur、uz分别为径向位移、轴向位移,m;σr为径向应力,Pa;σθ为周向应力,Pa;σz为轴向应力,Pa;α为热膨胀率,K-1;εp、dεp分别为塑性应变量和塑性应变增量;εcreep、dεcreep分别为蠕变应变量和蠕变应变增量;εintrinsic为本征应变量,如芯块密实化应变、辐照肿胀应变、材料热膨胀应变;E为杨氏模量,Pa;ν为泊松比。

二氧化铀燃料芯块随燃耗加深将产生辐照肿胀和密实化等本征应变。本文采用MATPRO[17]中的模型计算燃料芯块的辐照肿胀。固态裂变产物引起的肿胀较小,并且与燃耗呈正比,变化规律明确,通过式(17)来计算。

(17)

气态裂变产物引起的辐照肿胀采用半经验模型进行模拟,如式(18)所示。

e-0.016 2(2 800-T)·e-0.017 8ρBu

(18)

运行过程中,随着燃耗的加深,二氧化铀的塑形流动造成了芯块内部孔隙的逐渐消失从而使得芯块体积变小,燃料芯块密度增加,发生密实化。密实化造成的燃料芯块尺寸变化[18]由式(19)计算。

(19)

2 程序开发及验证

2.1 程序改造与计算流程

根据上述模型在FROBA-KJD程序[16]基础上开发燃料质量迁移模块和热电转换模块,并根据热电转换模型对热工计算模块的发射极和接收极温度求解进行改造,形成单节热离子燃料元件稳态性能分析程序,计算流程如图3所示。每个时间步内,在原有热工-机械耦合基础上增加热电转换计算,形成热工-热电-机械耦合,以考虑单节热离子燃料元件热电转换对材料间传热的影响。完成耦合计算后开展燃料质量迁移计算,以评估燃料芯块在质量迁移作用下发生的变形量和功率轴向分布变化。

图3 改进程序计算流程图

2.2 程序验证

程序热电转换模块和燃料质量迁移模块计算可靠性在之前研究中已得到验证[19-20]。为进一步确保程序计算结果的可靠性,使用程序对中国原子能科学研究院开展的热离子燃料元件堆内试验进行计算,通过将计算值与试验中测得指定位置温度对比进行热工计算模块验证。

中国原子能科学研究院堆内试验件几何结构和对应尺寸列于表2,冷却剂边界条件列于表3。试验计算采用的轴向功率密度如图4所示,功率密度轴向分布确定方法为:燃料总长130 mm,无贫铀条件;计算过程中取每5 mm长的平均值计算轴向的热中子通量密度分布,并以中心5 mm的平均通量密度进行归一化处理;以MCNP计算的轴向热中子通量密度分布值、2014年7月测量所得芯块内均匀段热中子通量密度为测量的准确值推导得出在满功率运行条件下轴向功率分布。该试验件长度、功率分布和冷却剂边界均与实际单节热离子燃料元件存在差异(单节热离子燃料元件活性区长度为37.5 mm,由液态NaK冷却),但径向几何结构和材料基本一致,能够为本程序提供热工模块计算验证。

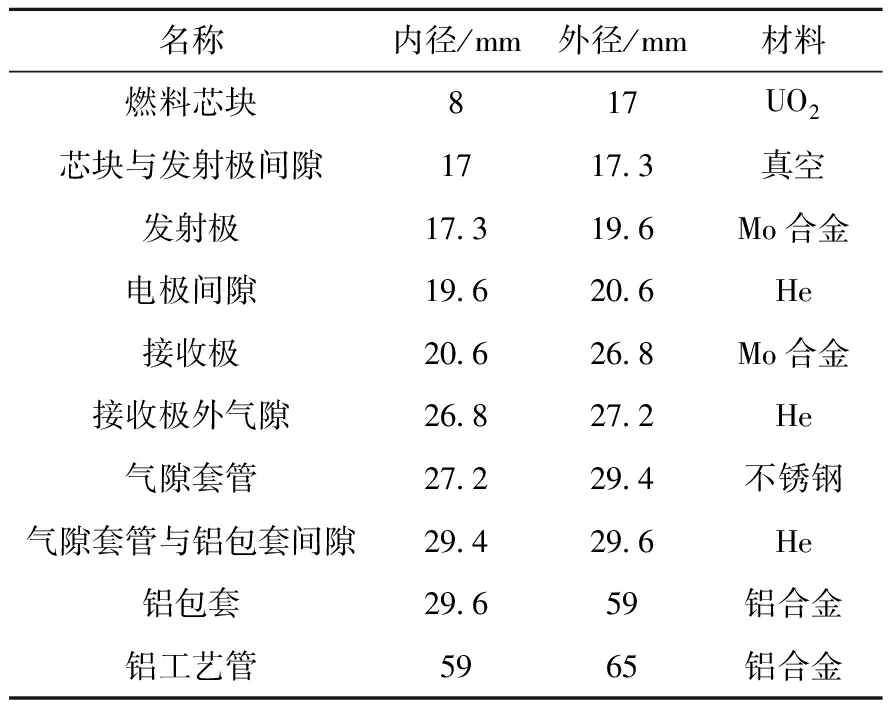
表2 堆内试验件各部件关键尺寸和材料

表3 堆内试验件冷却剂边界条件

图4 轴向功率密度分布

活性区中间高度位置最具代表性,对该位置热电偶测得温度进行对比。每次试验测得各测点温度随时间变化,但反应堆运行过程中功率出现波动,因此根据温度变化选择较稳定的区段计算平均值进行对比。以试验测得中间高度中心孔道温度随时间变化为例(图5),选取第250～12 800 min时间点为稳定段,得到平均温度为1 982.2 ℃。试验测得不同部件中间位置的温度平均值列于表4。

表4 试验测量平均温度及与计算温度的相对偏差

图5 试验温度对比区段选择

本程序计算得到温度径向分布与历次试验测得温度平均值如图6所示,程序计算结果与试验平均温度相对偏差列于表4,芯块内外壁面、接收极外壁面温度程序计算结果与试验值相对偏差均小于5%,说明本程序计算结果的有效性。

图6 试验件中间高度径向温度分布

3 单节热离子燃料元件稳态性能分析

对单节单节热离子燃料元件开展稳态工况模拟并进行质量迁移行为和稳态性能分析。单节热离子燃料元件几何结构及对应尺寸列于表5,冷却剂边界和输出电压等其他输入参数列于表6。单节热离子燃料元件以热功率3 500 W运行3 a,轴向上为余弦功率分布,径向功率分布如式(20)所示。

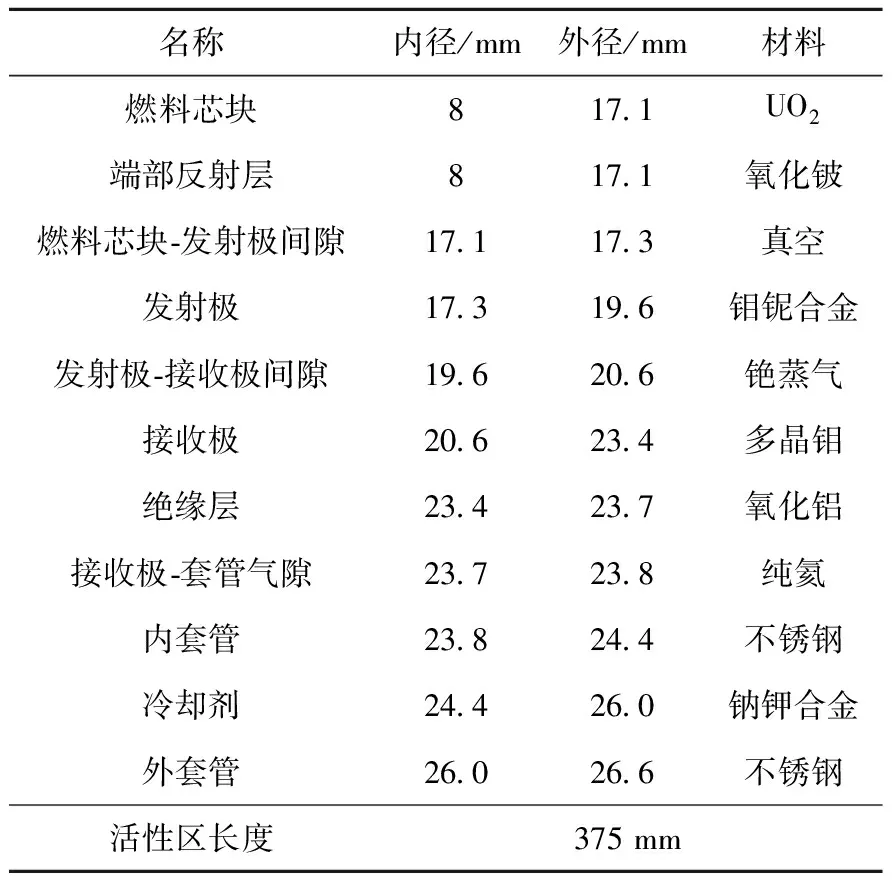
表5 单节热离子燃料元件各部件关键尺寸和材料

表6 计算采用的运行参数和计算条件

qv(r,z)=qv(R,0)×

(20)

式中:qv(r,z)为燃料体积释热率,W·m-3;qv(R,0)为燃料中间高度最外层R处的体积释热率,W·m-3;Heff为活性区有效高度,m。

3.1 燃料质量迁移行为分析

初始时刻轴向质量迁移成分饱和压力沿轴向分布如图7所示,可见各种铀氧化物饱和压力轴向分布与燃料芯块温度轴向分布一致,并且由于采用亚化学计量比燃料芯块,UO2饱和压力远高于UO和UO3。UO2饱和压力最高可达到0.14 Pa,而UO饱和压力最高为0.01 Pa、UO3饱和压力最高仅为2.92×10-5Pa,说明运行初期轴向质量迁移的主要成分为UO2。

图7 铀氧化物饱和压力轴向分布

以UO2为例研究轴向质量迁移流量沿轴向分布及其随时间的变化。初始时刻UO2质量流量轴向分布如图8所示,流动以向上为正方向。由流量大小沿轴向变化整体趋势可见燃料芯块中心孔道内燃料在中部高温处蒸发,而在两侧低温处凝结。UO2质量流量最高为1.50×10-3g·h-1,在中心孔道开放端仅为1.30×10-5g·h-1,是最高流量的0.87%。

图8 UO2质量流量轴向分布

燃料芯块内壁面即中心孔道壁面基准半径(不考虑燃料芯块的应变)轴向分布随时间的变化如图9所示,可见随着轴向燃料质量迁移进行,中段温度较高中心孔道半径不断增大,最终达到5.28 mm;而两侧温度较低区域的中心孔道半径不断减小,最小半径为1.21 mm。中心孔道半径最小位置之所以未出现在温度最低的两端,是因为燃料的轴向质量迁移同时受到温度和迁移距离影响。距离中间高度越远,燃料芯块内壁面温度越低,饱和压力也越低,但由角系数表达式可知同时从中间高度蒸发的燃料能够无碰撞到达该位置的概率也越低。因此在距离和温度的综合作用下,两个低温区域的中心孔道半径最小值位置与中心孔道两端存在一定距离。

图9 中心孔道基准半径轴向分布随时间的变化

改变单节热离子燃料元件中心孔道初始半径和热功率分析轴向质量迁移速率特性。不同初始半径下中心孔道半径最小值随时间的变化如图10所示。可见随着中心孔道初始半径增大,燃料芯块体积减小,功率密度上升,导致壁面温度随之上升,加剧轴向质量迁移。因此在运行结束时,不同中心孔道初始半径的单节热离子燃料元件最终中心孔道最小值差距小于初始时刻。不同热功率下中心孔道半径最小值随时间的变化如图11所示,可见随热功率上升,燃料芯块温度上升,燃料轴向质量迁移速率随之上升,中心孔道半径最小值下降速度也随之加快。当热功率上升至4 000 W时,中心孔道甚至发生堵塞。因此为避免中心孔道发生堵塞威胁单节热离子燃料元件的正常运行,需要合理选取初始中心孔道半径和与之匹配的热功率。

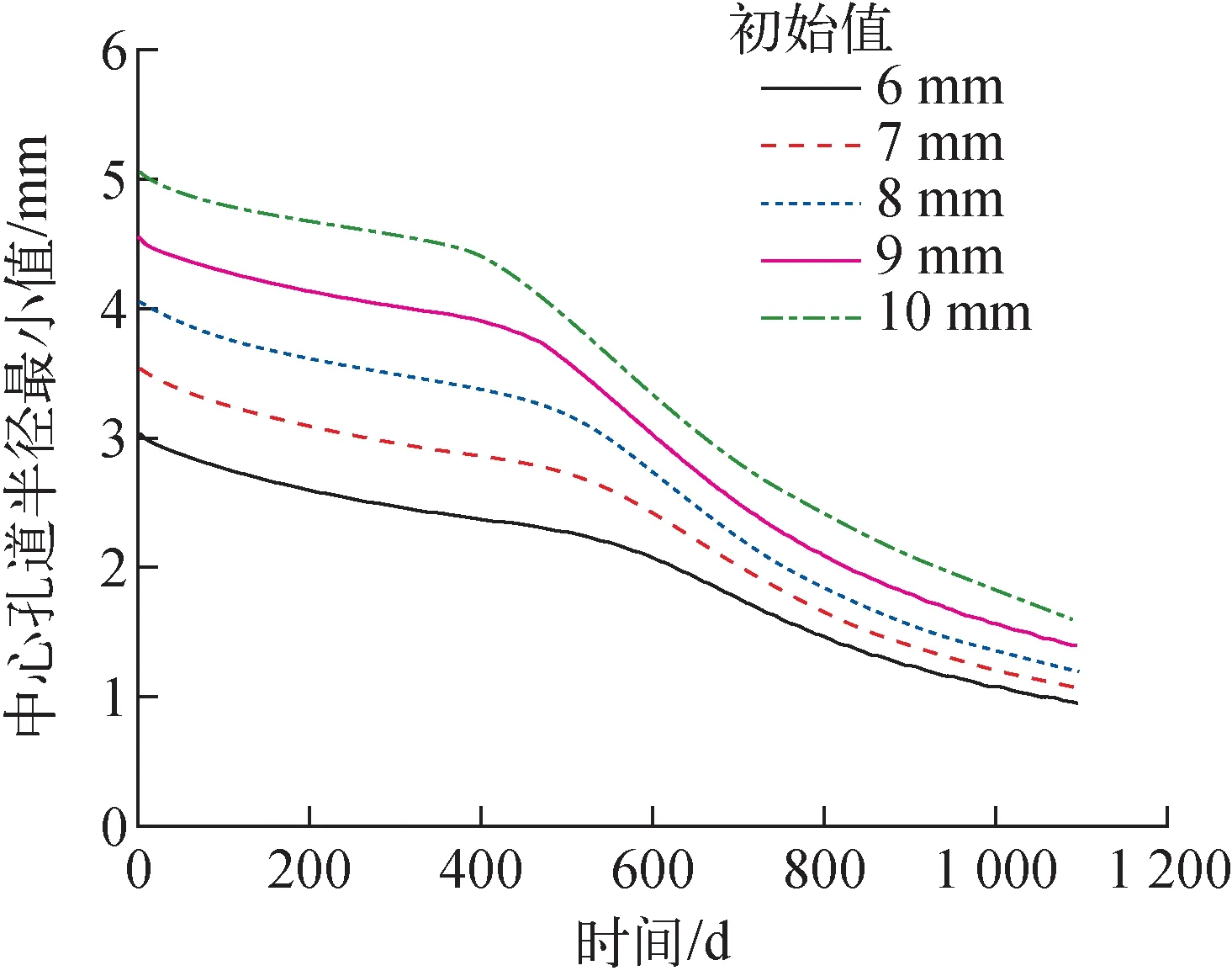
图10 不同初始半径下中心孔道半径最小值随时间的变化

图11 不同热功率下中心孔道半径最小值随时间的变化

3.2 热工性能分析

以线功率密度最高的中间高度(轴向第150节点)为例研究燃料元件径向温度分布,如图12所示。可见从燃料芯块内壁面向外温度逐渐降低,在各层材料之间的间隙存在明显的温差。从燃料芯块内壁面到内套管外壁面,总温差达到1 300.1 K,其中发射极和接收极的极间温差最大,达到893.7 K,占总温差的68.7%。由于燃料芯块以外各层材料较薄,内外壁面温差均很小,在燃料元件整体径向温度分布上几乎可以忽略。

图12 燃料元件轴向第150节点径向温度分布

燃料元件功率轴向分布随时间的变化如图13所示。随着高温处燃料向低温处迁移,燃料芯块的功率逐渐被展平。燃料元件中段高温区域由于燃料蒸发,轴向功率因子最大值由1.34下降至1.14;燃料元件两端低温区域由于燃料凝结,轴向功率因子最小值由0.39上升至0.47。燃料芯块内壁面温度轴向分布随时间的变化如图14所示,可见轴向质量迁移对轴向功率分布的影响及其对燃料芯块温度的影响十分明显。燃料芯块内壁面温度轴向分布在轴向质量迁移展平轴向功率和改变燃料芯块厚度影响下被展平。燃料芯块内壁面最高温度由2 129.2 K下降至2 025.5 K,最低温度由1 493.7 K上升至1 607.4 K,轴向最大温差由635.5 K下降至418.1 K,降幅达到34.2%。

图13 轴向功率因子轴向分布随时间的变化

图14 燃料芯块内壁面温度轴向分布随时间的变化

3.3 热电转换性能分析

热电转换是单节热离子燃料元件的关键功能。以初始时刻为例研究发射极和接收极电势轴向分布,如图15所示。发射极为正极(在电源内向接收极发射电子,因此电流方向为从发射极流出)且电流从两端流出,发射极电势为正且轴向分布上凸。发射极最高电势为1.38 V、最低电势为1.29 V,接收极为负极(在电源内接收电子,因此电流方向为向接收极流入)且电流从两端流入,所以接收极电势为负且轴向分布下凹。接收极最高电势为-0.017 V、最低电势为-0.048 V。由于发射极和接收极各自两端导线电阻不同,发射极和接收极的电势极值所在轴向高度随之产生差异,发射极最大电势位于180.6 mm高度,而接收极最小电势位于205.6 mm高度,两者相差25.0 mm。

图15 发射极和接收极电势轴向分布

燃料元件单位长度发射电流轴向分布如图16所示。由于发射电流大小不仅受极间电压影响,还与发射极温度相关,因此轴向分布不及极间电压轴向分布光滑,但由于极间电压和发射极温度轴向分布均为中间高、两边低,因此电流分布总体上也表现出相同趋势。单位长度发射电流最高为0.74 A·mm-1。输出电功率和热功率随时间的变化如图17所示,可见输出电功率出现小幅下降。这是因为轴向质量迁移对燃料元件轴向功率分布和发射极温度具有展平作用,因此发射极温度整体降低,使得输出电功率开始降低,由189.8 W最终下降至176.3 W,降幅为7.1%。

图16 发射电流轴向分布

图17 热功率和输出电功率随时间的变化

3.4 机械力学性能分析

燃料芯块外壁面半径随时间的变化如图18所示。燃料芯块外壁面半径主要受轴向质量迁移和辐照肿胀影响。燃料元件中段高温处燃料蒸发区域燃料芯块较薄且功率较高,辐照肿胀较早达到饱和,而两端低温处燃料凝结区域燃料芯块较厚,辐照肿胀贡献比高温处更高,因此轴向上燃料芯块外壁面半径呈现两端高、中间低趋势。运行结束时燃料芯块最大外壁面半径为8.98 mm,最小为8.43 mm。

图18 燃料芯块外壁面半径轴向分布随时间的变化

为对比分析燃料轴向质量迁移时蒸发和凝结对发射极变形的影响,选取运行结束时中心孔道半径最大的轴向第150节点和半径最小的轴向第270节点研究径向质量迁移对发射极变形的影响。发射极内壁面径向应力随时间的变化如图19所示。第150节点线功率密度和燃料芯块温度较高,径向质量迁移速率较高,导致发射极和燃料芯块在运行初期即发生接触,并产生明显径向应力,最大为0.97 MPa。随着轴向质量迁移展平功率分布导致燃料芯块和发射极温度降低,接触作用逐渐减轻,径向应力也随之减小。轴向第270节点处温度较低,径向质量迁移速率较慢,较第150节点稍晚发生接触和产生明显径向应力,应力最大值亦小于第150节点,但由于该位置燃料不断凝结并发生辐照肿胀,燃料芯块和发射极始终维持较强接触作用,发射极径向应力减小速度明显慢于第150节点,使得发射极在单节热离子燃料元件运行过程中持续发生蠕变。

图19 发射极内壁面径向应力随时间的变化

发射极内外壁面周向应变随时间的变化如图20所示。结合如图21、22所示轴向第150节点和轴向第270节点发射极外壁面各项周向应变随时间的变化可见,发射极未发生塑性变形;热膨胀随轴向质量迁移影响发生小幅变化,第150节点处燃料蒸发、温度下降,热膨胀小幅减小,反之第270节点处热膨胀小幅增大;发射极应变主要受与燃料芯块接触下受压发生蠕变主导。轴向第150节点因燃料芯块辐照肿胀达到饱和且轴向质量迁移使该位置温度降低,蠕变应变在上升约400 d后即趋于稳定,外壁面周向应变最大值为0.026。轴向第270节点处发射极则由于燃料凝结和温度上升发生蠕变,蠕变应变不断上升,外壁面周向应变最终达到0.033。

图20 发射极内外壁面周向应变随时间的变化

图21 轴向第150节点发射极外壁面周向应变随时间的变化

图22 轴向第270节点发射极外壁面周向应变随时间的变化

发射极外壁面半径随时间的变化如图23所示,可见由于发射极和燃料芯块接触,发射极外壁面半径轴向分布受燃料芯块变形主导,变化趋势与燃料芯块外壁面变形一致,在轴向质量迁移和辐照肿胀作用下形成区别于轴向功率分布和温度分布的两端高、中间低趋势,运行结束时发射极最大外壁面半径为10.09 mm。

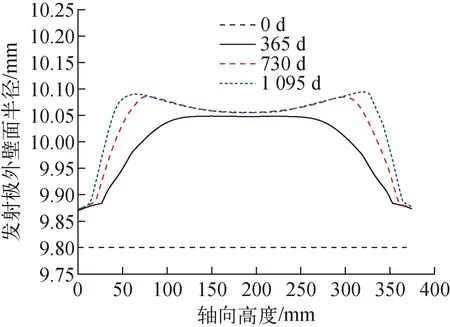
图23 发射极外壁面半径轴向分布随时间的变化

4 结论

通过建立燃料质量迁移模型和热电转换模型开发了单节热离子燃料元件稳态性能分析程序,经过与中国原子能科学研究院堆内试验结果对比进一步验证程序热工计算功能后,开展单节热离子燃料元件质量迁移行为模拟及其对燃料元件性能影响分析,得到结论如下。

1) 亚化学质量比下燃料质量迁移主要成分为UO2,轴向质量迁移显著改变燃料芯块中心孔道形貌,中心孔道最小半径减小至1.21 mm。当热功率上升时,中心孔道存在堵塞风险。

2) 燃料轴向质量迁移展平单节热离子燃料元件轴向功率分布,进而展平燃料元件轴向温度分布,轴向最大温差由635.5 K下降至418.1 K,降幅达到34.2%。

3) 在燃料轴向质量迁移展平温度分布影响下,单节热离子燃料元件输出电功率小幅下降,但维持在175 W以上。

4) 径向质量迁移是燃料芯块和发射极在运行初期即发生接触,发射极在接触压力下发生蠕变。在轴向质量迁移影响下,燃料凝结处发射极蠕变大于燃料蒸发处,轴向半径分布形成两端高、中间低趋势。

在后续研究中可进一步考虑和研究高温导致燃料芯块重结构及其对燃料芯块热工机械性能相关物性的影响,对单节热离子燃料元件稳态热工机械等性能进行更深入分析。