基于正交曲线网格的河道地形插值方法及应用

郑军 张辛 刘清兰 凡姚申 窦身堂 于守兵

摘 要：传统的插值方法在采样河道地形横断面分布稀疏情况下，无法有效获得弯曲河道高精度插值结果，亟须研究有效的弯曲河道地形插值新方法，对河道演变及其规律进行定量分析。为此，提出了一种基于正交曲线网格的河道地形插值方法（ＯＣＧＩ），首先沿横断面进行线性插值，然后沿纵向网格线进行插值，弥补了纵向采样点空间分布不足的缺陷，且考虑了河势变化，将插值范围控制在网格分布的区域。应用实例表明：该方法比反距离加权法（ＩＤＷ）和普通克里金法（ＫＧ）能得出更合理的结果，可应用于黄河口尾闾等弯曲河道的地形插值。

关键词：弯曲河道；地形插值；正交曲线网格；断面高程

中图分类号：Ｐ３３３；ＴＶ８８２．１ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２３．０７．０１２

引用格式：郑军，张辛，刘清兰，等．基于正交曲线网格的河道地形插值方法及应用［Ｊ］．人民黄河，２０２３，４５（７）：６２－６７．

河道地形是河流地貌演变分析、泥沙冲淤计算和水流泥沙输运数值模拟的基础［１－３］ 。虽然摄影测量、基于光谱的深度检索和激光探测等遥感技术可以提供大面积、高精度河道形态信息［４－６］ ，但这些数据并不是常规可用的，大多数河流地貌研究仍依赖于全站仪、经纬仪或全球定位系统等常规地面测量设备［７－１０］ 。这些方法提供了所选位置河床高程的点数据，需要采用某种形式的空间插值方法将测量产生的离散高程点构造成河道高程面，以满足河道地形可视化、河道体积计算或河道建模的需要［１１］ 。

有许多经典的空间插值方法，如反距离加权（ＩＤＷ）［１２］ 、不规则三角网（ ＴＩＮ）［１３］ 、普通克里金（ＫＧ）［１４］ 、通用克里金（ＵＫＧ）［１５］ 和多元二次径向基函数（ＭＲＢＦ）等［１６］ ，不同方法的插值结果可能存在很大差异，并且没有一种最优插值方法来解决所有的插值问题。特殊河道（如弯曲河道的凹岸凸岸附近）的地形插值对于河道地形相关变量的计算非常重要。通常实测一个横截面上采样点的距离从几十米到几百米不等，而河道横断面之间的距离从几百米到几千米不等，使用这些经典插值方法可能无法获得较高的插值精度［１７］ 。例如，对于大量异常三角形单元，使用ＩＤＷ 和ＴＩＮ 方法可能会增加插值误差［１８］ 。与横向相比，沿纵向实测的数据点较少，并且许多经典插值方法无法有效地考虑河流平面形态［１９］ ，插值得到的河道ＤＥＭ 可能充斥大量的无效数据［２０］ ，因此使用ＩＤＷ 或径向基函数等邻近方法可能无法改善结果。

本研究提出了一种新的河道拟合正交曲线网格线性插值方法（ｂａｓｅ ｏｎ Ｏｒｔｈｏｇｏｎａｌ Ｃｕｒｖｉｌｉｎｅａｒ Ｇｒｉｄ Ｉｎ⁃ｔｅｒｐｏｌａｔｉｏｎ，ＯＣＧＩ），主要步骤：

１）提取河道边界，确定空间插值的范围，生成一组适应河道边界平面形态的正交曲线网格。靠近横截面的横向网格线应平行或适合横截面。

２）求出曲线网格系统中每个测量截面的列数，然后使用截面数据和线性插值方法对横向网格点处的数据进行插值。

３）使用线性插值方法沿相邻横截面之间的主河道纵向插值多余网格点。

４）基于密集网格点处的插值，使用经典插值方法进行第二次插值。插值方法的本质是线性算法，因此该方法与对偶线性和三角网插值方法具有相同的精度。本研究还参考了几种经典的插值算法进行比较，如ＩＤＷ、ＫＧ。

１ 基于正交网格的插值理论

本文采用基于复变函数理论的网格生成方法生成正交曲线网格［２１］ 。受河道与水流的长期相互作用影响，河道的主轴通常与主流大致平行，河道地形沿主河道纵向的空间变化远小于沿横向的空间变化，通常取样横截面垂直于主流或主河道的方向。横截面与网格横线之间的角度加大可能会降低插值精度［２２］ 。为了避免大角度的出现，进而提高插值精度，在生成正交曲线网格的过程中，调整网格横截面附近的横截面线，使其尽量与有实测已知地形数据的横截面重合。正交曲线网格和横截面的分布如图１ 所示。

计算采样点每个横截面的列阶ｉ，然后基于横截面数据和线性插值方法对每个横网格点（ｉ， ｊ）处的变量值进行插值。基于网格点位置Ｐ（ｉ， ｊ），分别计算沿横截面的两个相邻采样点Ａ（ｎ， ｍ）和Ａ（ｎ， ｍ ＋１）。使用的线性插值公式为

２．２ 理想河道插值结果比较

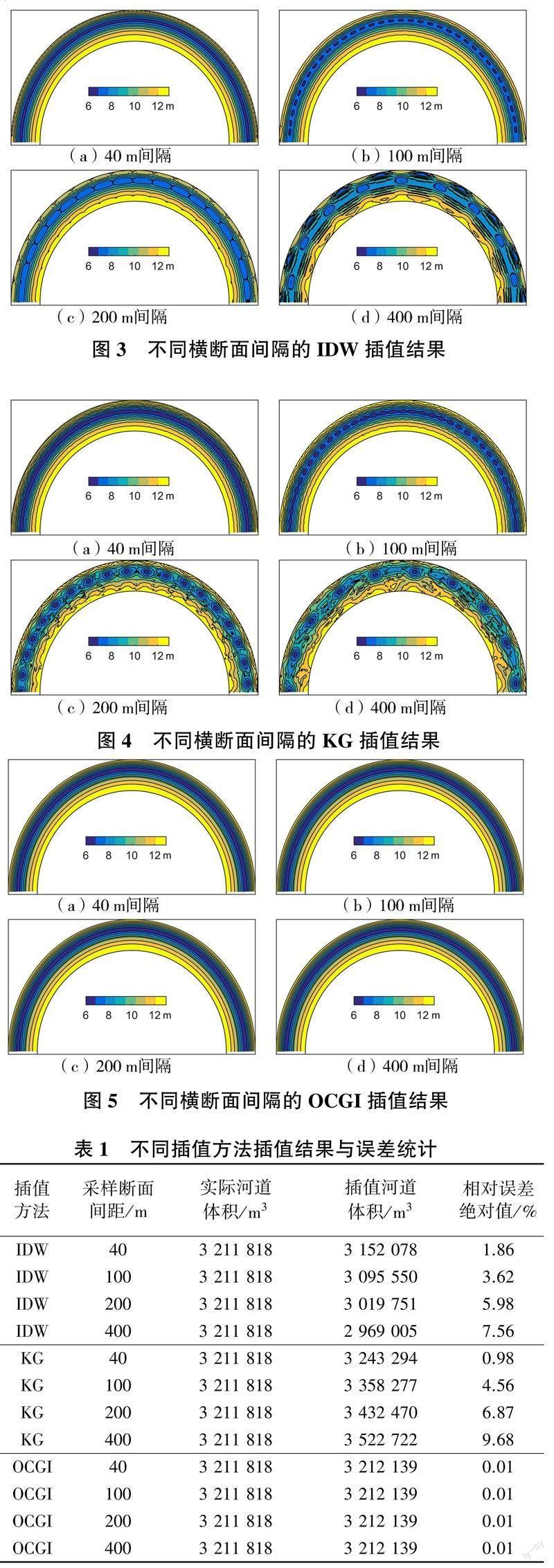
设置４０、１００、２００、４００ ｍ 四种采样横断面间距，采用ＩＤＷ、ＫＧ 和ＯＣＧＩ 插值方法所得插值结果分别如图３、图４、图５ 所示，将各种插值结果所得到的河道体积与实际河道体积进行比较，统计它们的相对误差，结果见表１。可以看出，在采样断面足够密集（４０ ｍ 横断面间隔）的情况下，ＩＤＷ 和ＫＧ 的相對误差绝对值小于２．００％，尤其是ＫＧ 插值，可以得到精度相对较高的插值结果。但是当横断面间隔距离较大时，存在较大误差。比如横断面间隔为４００ ｍ 时，ＩＤＷ 的插值误差达７．５６％，ＫＧ 的插值误差高达９．６８％，插值地形图显示，河流谷线沿线分布一系列不合理的孤立、封闭的等高线，而这些地形信息对分析河流地貌演变及河道航运是有影响的。ＯＣＧＩ 插值方法不受采样断面间距的影响，无论断面间隔４０ ｍ 还是４００ ｍ 都能插值得到与实际地形高度一致的结果，其原因是构造的理想河道高程等值线平行于河道边界，也就是说正交曲线网格纵向上不同位置插值点的高程值相同，用不同间距横断面插值获得的结果，其相对误差保持不变。

通过以上的对比分析，可以得出以下结论：

１）基于河道稀疏采样横断面插值，ＩＤＷ 和ＫＧ 方法可能会导致较大的误差，而本文提出的ＯＣＧＩ 插值方法可以获得较高插值精度，与ＩＤＷ 和ＫＧ 方法相比，误差最小。

２）随着采样横断面间距的增大，基于ＩＤＷ 插值结果的河道体积大于真实值，而ＫＧ 的河道体积小于真实值。

３）当采样横断面密集时，ＩＤＷ 的插值精度优于ＫＧ 的，而当采样横断面相对较稀疏时，ＫＧ 的插值精度优于ＩＤＷ 的，但都劣于本文提出的ＯＣＧＩ 插值方法。

２．３ 黄河口尾闾河道插值

黄河口尾闾河道是黄河水沙入海的最后通道，是河海交互作用的焦点区域［２３］ ，同时受径流水沙条件、海洋动力以及人类活动等多重影响，其摆动、出汊、改道频繁［２４］ ，是河流地貌学研究的热点［２５－２７］ 。本研究以黄河利津以下长约１０６ ｋｍ 的尾闾河道为例，进一步验证ＯＣＧＩ 河道地形插值方法在自然河道中的适用性。

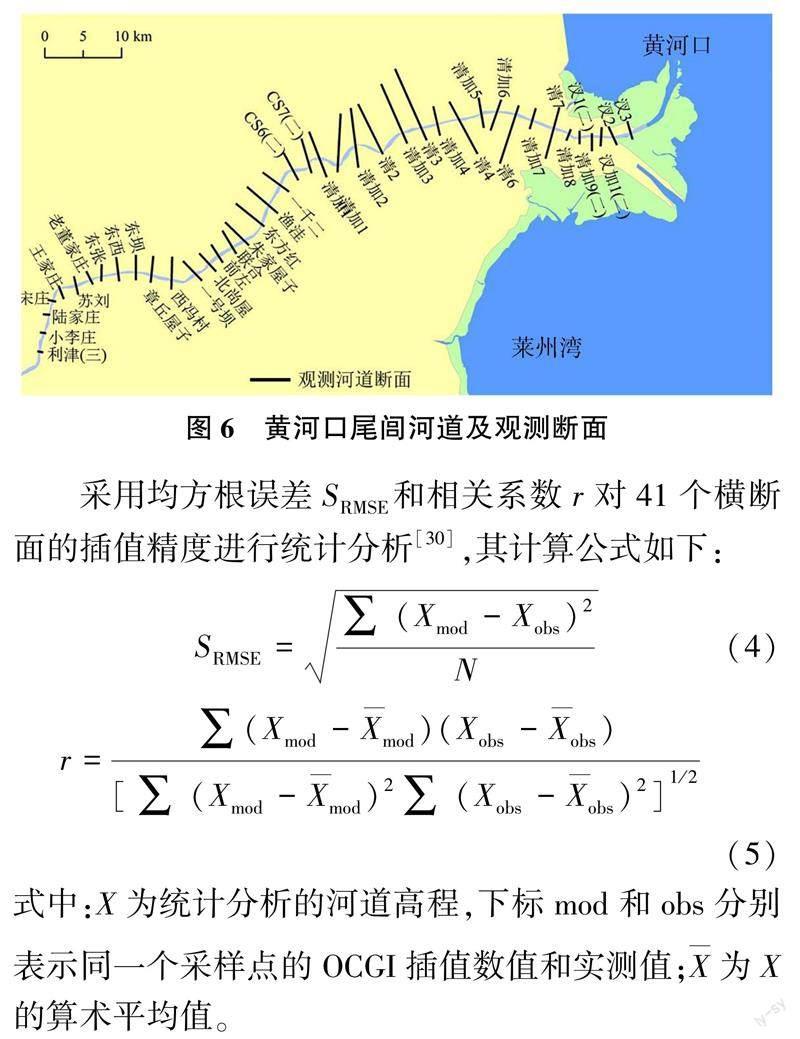
所用数据包括河道断面高程数据以及卫星遥感数据。断面高程数据为２０１７ 年黄河水利委员会统测黄河下游断面高程数据，黄河口尾闾河段共有固定断面４１ 个（见图６），断面间距２～６ ｋｍ。卫星遥感数据为Ｌａｎｄｓａｔ８ 遥感影像数据，从美国地球资源与科学中心网站免费下载，其最高分辨率为１５ ｍ，被广泛应用于河流水文地貌研究［２８－２９］ 。本文选取２０１７ 年汛后与断面测量时间最为接近的无云或少云遮挡的研究区遥感影像数据。根据遥感影像提取河道边界，建立与河道边界贴合的正交曲线网格，插值过程在这个网格分布范围内进行。这样就相当于考虑了河势变化，避免插值结果不顺应河势而产生连续的河道地形面。网格线垂直于河道的横断面和沿河道的纵断面，每个横断面的点数保持一致，靠近实测断面的横断面调整到与实测断面位置尽量重合或平行，网格边长控制在３０～１００ ｍ 范围内。

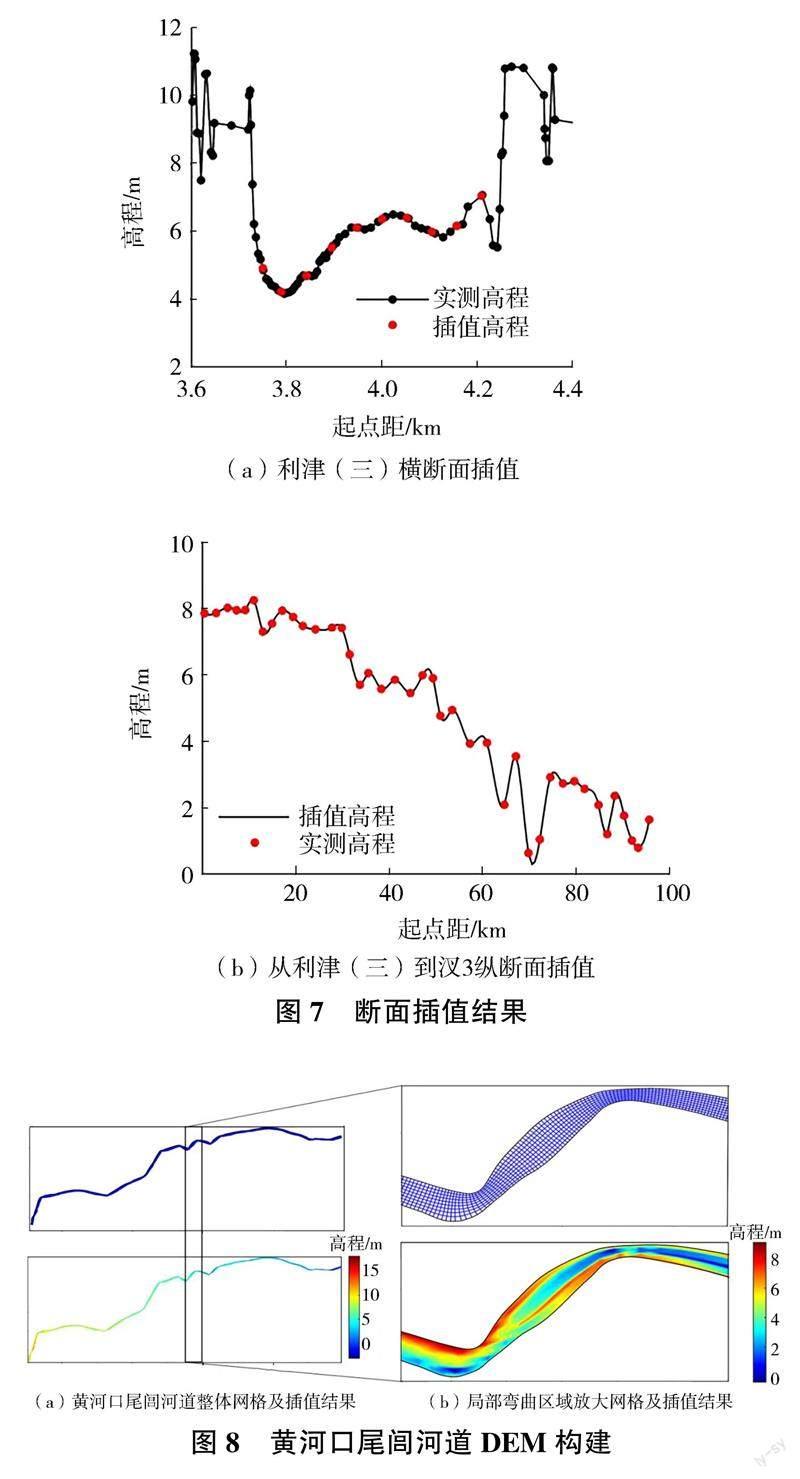
使用ＯＣＧＩ 插值方法先进行横断面插值，补充横向上网格点的采样数据，其中一个横断面的插值结果如图７（ａ）所示。４１ 条横断面的插值与实测值的均方根误差在０．０２～０．０８ ｍ 范围内，相关系数高达０．９８２。横断面插值完成后，再进行纵断面插值，其中一个纵断面的插值结果如图７（ｂ）所示。１０ 个纵断面的插值与实测值的均方根误差均在０．０６～０．１２ ｍ 范围内，相关系数稍低于横断面插值的，为０．９６５。

横向、纵向插值完成后，每个网格点上都有一个高程值，再利用经典插值方法进行第二次插值，完成河道地形模型构建。图８（ａ）展示了黄河口尾闾河道整体网格分布和插值结果，可以看出黄河口尾闾河道从上游到下游高程逐渐降低的趋势，局部弯曲区域放大的插值结果也清晰地显示出河道深槽浅滩的分布格局，见图８（ｂ）。由此可见，该河段深槽和浅滩交错分布，ＯＣＧＩ 插值较好地刻画了河道地形空间变化。

３ 讨论

河道地形插值的实质是将离散的空间采样点转化为连续曲面。地形插值的方法很多，主要分为确定性插值和地统计插值两类方法。ＩＤＷ 是一种确定性插值方法，通过周围测量点的值内插或者通过特定的数学公式来内插，而较少考虑测量点的整体空间分布情况。ＫＧ 是一種地统计插值法，它建立在对测量点的空间自相关分析基础上，依据自然现象的空间变异规律进行插值。然而，当河道实测横断面之间的距离超过一定值后，使用这两种方法都无法获得较高的插值精度。

本文提出的ＯＣＧＩ 插值方法，不仅借鉴确定性插值的做法，采用经典概率论和数理统计原理对横向、纵向断面分别进行线性内插，而且考虑了测量点的空间相关性，即用正交网格曲线的河势方向作为插值方向，依据河道地形随河势变化的空间自然变化规律进行插值，符合河道地形的纵深变化，能够利用有限的断面数据较为准确地重构河道地形。使用理想河道来验证ＯＣＧＩ 插值方法的有效性，简化了河道地形，一方面说明该方法在地形插值中的特点，即使用了纵向插值，如果纵向上高程不变，插值的结果将不受横断面间距影响，另一方面也突显该方法与ＩＤＷ 和ＫＧ 方法相比的优越性。

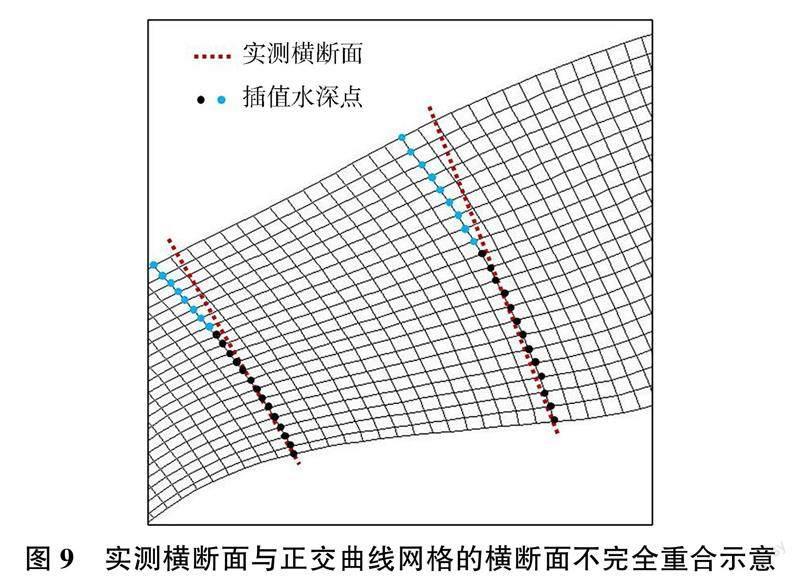
在实际插值过程中，ＯＣＧＩ 插值方法构建的正交曲线横断面与实测横断面的位置偏差会给插值结果带来系统误差。在构造正交曲线网格时，横断面不能保证与每一条实测横断面重合，只能最大限度地垂直于主流线。实测横断面理应垂直于主流线，但实测横断面位置实际上由现场地形测量人员早期人为而定，随着河势的变化，可能已经不再垂直于主流线，这就使得实测横断面与正交曲线网格的横断面不完全重合（见图９）。在实际插值过程中，横向插值使用的部分已知数据可能不是插值点位置的数据，如图９ 所示，蓝色插值点数据的获得，使用的是距离最近的已知测量点的实测值，而它们在空间位置上不完全重合。

４ 结论

通过比较几种河道地形空间插值方法在不同类型采样数据中的插值结果，得出以下主要结论。

１）在采样点空间分辨率足够高的情况下，使用经典插值方法（如ＴＩＮ、ＫＧ 和ＩＤＷ）可以获得准确的结果，但当横截面采样点稀疏时，ＫＧ 和ＩＤＷ 的插值精度较低。

２）提出了一种新的插值方法ＯＣＧＩ，基于正交曲线网格系统，先沿横断面插值，再沿纵向网格线进行插值，弥补了纵向采样点空间分布不足的缺陷，可以在稀疏横断面情况下获得较准确的河道地形数据。

３）ＯＣＧＩ 插值方法沿河道边界设置正交曲线网格，将插值范围控制在正交曲线网格分布的区域，考虑了河势变化，避免了插值结果不顺应河势而产生的连续地形面。当使用横断面高程数据对弯曲河道大范围插值时，可以显著改善河道地形插值结果。利用黄河口尾闾河道进行ＯＣＧＩ 插值方法实例验证，得到了较好的效果。

参考文献：

［１］ ＬＡＮＥ Ｎ Ｓ，ＷＥＳＴＡＷＡＹ Ｍ Ｒ，ＨＩＣＫＳ Ｍ Ｄ．Ｅｓｔｉｍａｔｉｏｎ ｏｆＥｒｏｓｉｏｎ ａｎｄ Ｄｅｐｏｓｉｔｉｏｎ Ｖｏｌｕｍｅｓ ｉｎ ａ Ｌａｒｇｅ， Ｇｒａｖｅｌ⁃Ｂｅｄ，Ｂｒａｉｄｅｄ Ｒｉｖｅｒ Ｕｓｉｎｇ Ｓｙｎｏｐｔｉｃ Ｒｅｍｏｔｅ Ｓｅｎｓｉｎｇ［Ｊ］．Ｅａｒｔｈ Ｓｕｒ⁃ｆａｃｅ Ｐｒｏｃｅｓｓｅｓ ａｎｄ Ｌａｎｄｆｏｒｍｓ，２００３，２８（３）：２４９－２７１．

［２］ ＦＵＬＬＥＲ Ｉ Ｃ， ＬＡＲＧＥ Ａ Ｒ Ｇ， ＭＩＬＡＮ Ｄ Ｊ． ＱｕａｎｔｉｆｙｉｎｇＣｈａｎｎｅｌ Ｄｅｖｅｌｏｐｍｅｎｔ ａｎｄ Ｓｅｄｉｍｅｎｔ Ｔｒａｎｓｆｅｒ ＦｏｌｌｏｗｉｎｇＣｈｕｔｅ Ｃｕｔｏｆｆ ｉｎ ａ Ｗａｎｄｅｒｉｎｇ Ｇｒａｖｅｌ⁃Ｂｅｄ Ｒｉｖｅｒ［Ｊ］．Ｇｅｏｍｏｒ⁃ｐｈｏｌｏｇｙ，２００３，５４（３）：３０７－３２３．

［３］ ＭＥＩ Ｘ Ｆ，ＤＡＩ Ｚ Ｊ，ＤＡＲＢＹ Ｓ Ｅ，ｅｔ ａｌ．Ｌａｎｄｗａｒｄ Ｓｈｉｆｔｓ ｏｆ ｔｈｅＭａｘｉｍｕｍ Ａｃｃｒｅｔｉｏｎ Ｚｏｎｅ ｉｎ ｔｈｅ Ｔｉｄａｌ Ｒｅａｃｈ ｏｆ ｔｈｅＣｈａｎｇｊｉａｎｇ Ｅｓｔｕａｒｙ Ｆｏｌｌｏｗｉｎｇ Ｃｏｎｓｔｒｕｃｔｉｏｎ ｏｆ ｔｈｅ ＴｈｒｅｅＧｏｒｇｅｓ Ｄａｍ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０２１，５９２：１２５７８９．

［４］ 曲伟，庞治国，雷添杰，等．中小河流治理及监测监管中的遥感技术应用综述［Ｊ］．水利水电技术（中英文），２０２１，５２（７）：２３－３２．

［５］ 張树文，蔡红艳，匡文慧，等．基于遥感技术的黑龙江上中游河道特征研究［Ｊ］．地理科学，２００９，２９（６）：８４６－８５２．

［６］ ＬＥＧＬＥＩＴＥＲ Ｊ Ｃ，ＲＯＢＥＲＴＳ Ａ Ｄ，ＭＡＲＣＵＳ Ａ Ｗ，ｅｔ ａｌ．Ｐａｓ⁃ｓｉｖｅ Ｏｐｔｉｃａｌ Ｒｅｍｏｔｅ Ｓｅｎｓｉｎｇ ｏｆ Ｒｉｖｅｒ Ｃｈａｎｎｅｌ Ｍｏｒｐｈｏｌｏｇｙａｎｄ ｉｎ⁃Ｓｔｒｅａｍ Ｈａｂｉｔａｔ： Ｐｈｙｓｉｃａｌ Ｂａｓｉｓ ａｎｄ Ｆｅａｓｉｂｉｌｉｔｙ［Ｊ］．Ｒｅｍｏｔｅ Ｓｅｎｓｉｎｇ ｏｆ Ｅｎｖｉｒｏｎｍｅｎｔ，２００４，９３（４）：４９３－５１０．

［７］ ＫＥＩＭ Ｒ Ｆ，ＳＫＡＵＧＳＥＴ Ａ Ｅ，ＢＡＴＥＭＡＮ Ｄ Ｓ．Ｄｉｇｉｔａｌ ＴｅｒｒａｉｎＭｏｄｅｌｉｎｇ ｏｆ Ｓｍａｌｌ Ｓｔｒｅａｍ Ｃｈａｎｎｅｌｓ Ｗｉｔｈ ａ Ｔｏｔａｌ⁃Ｓｔａｔｉｏｎ Ｔｈｅ⁃ｏｄｏｌｉｔｅ［Ｊ］．Ａｄｖａｎｃｅｓ ｉｎ Ｗａｔｅｒ Ｒｅｓｏｕｒ，１９９９，２３（１）：４１－４８．

［８］ ＢＲＡＳＩＮＧＴＯＮ Ｊ，ＲＵＭＳＢＹ Ｂ Ｔ，ＭＣＶＥＹ Ｒ Ａ．Ｍｏｎｉｔｏｒｉｎｇ ａｎｄＭｏｄｅｌｌｉｎｇ Ｍｏｒｐｈｏｌｏｇｉｃａｌ Ｃｈａｎｇｅ ｉｎ ａ Ｂｒａｉｄｅｄ Ｇｒａｖｅｌ⁃ＢｅｄＲｉｖｅｒ Ｕｓｉｎｇ Ｈｉｇｈ Ｒｅｓｏｌｕｔｉｏｎ ＧＰＳ⁃Ｂａｓｅｄ Ｓｕｒｖｅｙ ［Ｊ］． ＥａｒｔｈＳｕｒｆａｃｅ Ｐｒｏｃｅｓｓｅｓ ａｎｄ Ｌａｎｄｆｏｒｍｓ，２０００，２５（９）：９７３－９９０．

［９］ 申冠卿，姜乃迁，张原锋，等．黄河下游断面法与沙量法冲淤计算成果比较及输沙率资料修正［Ｊ］．泥沙研究，２００６，３１（１）：３２－３７．

［１０］ 刘清兰，陈俊卿，陈沈良．调水调沙以来黄河尾闾河道冲淤演变及其影响因素［Ｊ］．地理学报，２０２１，７６（１）：１３９－１５２．

［１１］ 戚晓明，金菊良，朱兰保，等．河道湖泊地形的数字重构研究［Ｊ］．水利水电技术，２０１４，４５（９）：１２－１４，１８．

［１２］ ＬＥＧＬＥＩＴＥＲ Ｃ Ｊ， ＫＹＲＩＡＫＩＤＩＳ Ｐ Ｃ．Ｓｐａｔｉａｌ Ｐｒｅｄｉｃｔｉｏｎ ｏｆＲｉｖｅｒ Ｃｈａｎｎｅｌ Ｔｏｐｏｇｒａｐｈｙ ｂｙ Ｋｒｉｇｉｎｇ ［Ｊ］． Ｅａｒｔｈ ＳｕｒｆａｃｅＰｒｏｃｅｓｓｅｓ ａｎｄ Ｌａｎｄｆｏｒｍｓ， ２００８， ３３（６）：８４１－８６７．

［１３］ 柯晓山，张玮，王荣静，等．采用不规则三角网插值进行土地整理项目前期平整土方量的计算［Ｊ］．农业工程学报，２００４，２０（３）：２４３－２４７．

［１４］ 谢梦姣，王洋，康营，等．人工神经网络与普通克里金插值法对土壤属性空间预测精度影响研究［Ｊ］．生态与农村环境学报，２０２１，３７（７）：９３４－９４２．

［１５］ 杨雨亭，尚松浩，李超．土壤水分空间插值的克里金平滑效应修正方法［Ｊ］．水科学进展，２０１０，２１（２）：２０８－２１３．

［１６］ 蔡香玉，杨林，吕海洋．基于径向基函数神经网络的机载ＬｉＤＡＲ 点云空洞填补方法［Ｊ］．南京师范大学学报（工程技术版），２０１７，１７（３）：５７－６２．

［１７］ 方艺辉，陈兴伟．各向异性河床地形空间插值方法比较研究［Ｊ］．水文，２０２１，４１（５）：４３－４７．

［１８］ 华祖林，王海燕，汪靓，等．非连续河道地形插值方法的比选［Ｊ］．水利水电科技进展，２０１６，３６（３）：１６－１９，５１．

［１９］ ＭＥＲＷＡＤＥ Ｖ Ｍ，ＭＡＩＤＭＥＮＴ Ｄ Ｒ，ＧＯＦＦ Ｊ Ａ．ＡｎｉｓｏｔｒｐｉｃＣｏｎｓｉｄｅｒａｔｉｏｎｓ Ｗｈｉｌｅ Ｉｎｔｅｒｐｏｌａｔｉｎｇ Ｒｉｖｅｒ Ｃｈａｎｎｅｌ Ｂａｔｈｙｍｅｔｒｙ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２００６，３３１（３）：７３１－７４１．

［２０］ 白亮，王伟，原松，等．基于离散点的河道地形外包边界自动生成方法［Ｊ］．人民长江，２０２１，５２（３）：１１２－１１７．

［２１］ 戎贵文，魏文礼，刘玉玲，等．复杂边界正交曲线网格生成技术［Ｊ］．武汉大学学报（工学版），２０１０，４３（４）：４５４－４５７．

［２２］ 黄惠明，王义刚，杨同军，等．基于对流与扩散效应的非正交曲线网格生成及三维潮流数值模拟［Ｊ］．水力发电学报，２０１４，３３（２）：９７－１０４．

［２３］ 胡春宏，张治昊．黄河口尾闾河道横断面形态调整及其与水沙过程的响应关系［Ｊ］．应用基础与工程科学学报，２０１１，１９（４）：５４３－５５３．

［２４］ 张诗媛，夏军强，万占伟，等．黄河口尾闾河道近４０ 年河床断面及平面形态调整特点［Ｊ］．水力发电学报，２０１９，３８（１）：６３－７４．

［２５］ ＳＨＩ Ｃ，ＺＨＡＮＧ Ｄ．Ｐｒｏｃｅｓｓｅｓ ａｎｄ Ｍｅｃｈａｎｉｓｍｓ ｏｆ ＤｙｎａｍｉｃＣｈａｎｎｅｌ Ａｄｊｕｓｔｍｅｎｔ ｔｏ Ｄｅｌｔａ Ｐｒｏｇｒａｄａｔｉｏｎ：ｔｈｅ Ｃａｓｅ ｏｆ ｔｈｅＭｏｕｔｈ Ｃｈａｎｎｅｌ ｏｆ ｔｈｅ Ｙｅｌｌｏｗ Ｒｉｖｅｒ， Ｃｈｉｎａ ［ Ｊ］． ＥａｒｔｈＳｕｒｆａｃｅ Ｐｒｏｃｅｓｓｅｓ ＆ Ｌａｎｄｆｏｒｍｓ， ２００３， ２８（６）：６０９－６２４．

［２６］ ＢＩ Ｎ Ｓ，ＳＵＮ Ｚ Ｑ， ＷＡＮＧ Ｈ Ｊ，ｅｔ ａｌ．Ｒｅｓｐｏｎｓｅ ｏｆ Ｃｈａｎｎｅｌ Ｓｃｏｕ⁃ｒｉｎｇ ａｎｄ Ｄｅｐｏｓｉｔｉｏｎ ｔｏ ｔｈｅ Ｒｅｇｕｌａｔｉｏｎ ｏｆ Ｌａｒｇｅ Ｒｅｓｅｒｖｏｉｒｓ：ＡＣａｓｅ Ｓｔｕｄｙ ｏｆ ｔｈｅ Ｌｏｗｅｒ Ｒｅａｃｈｅｓ ｏｆ ｔｈｅ Ｙｅｌｌｏｗ Ｒｉｖｅｒ（Ｈｕａｎｇｈｅ）［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒｏｌｏｇｙ，２０１８，５６８：９７２－９８４．

［２７］ 赵翔，吉祖稳，王党伟，等．基于逻辑回归法预测黄河口尾闾河道出汊概率［Ｊ］．泥沙研究，２０２１，４６（３）：３６－４２．

［２８］ ＬＩ Ｐ，ＣＨＥＮ Ｓ Ｌ，ＪＩ Ｈ Ｙ，ｅｔ ａｌ．Ｃｏｍｂｉｎｉｎｇ Ｌａｎｄｓａｔ⁃８ ａｎｄＳｅｎｔｉｎｅｌ⁃２ ｔｏ Ｉｎｖｅｓｔｉｇａｔｅ Ｓｅａｓｏｎａｌ Ｃｈａｎｇｅｓ ｏｆ ＳｕｓｐｅｎｄｅｄＰａｒｔｉｃｕｌａｔｅ Ｍａｔｔｅｒ ｏｆｆ ｔｈｅ Ａｂａｎｄｏｎｅｄ Ｄｉｓｔｒｉｂｕｔａｒｙ Ｍｏｕｔｈｓ ｏｆＹｅｌｌｏｗ Ｒｉｖｅｒ Ｄｅｌｔａ［Ｊ］．Ｍａｒｉｎｅ Ｇｅｏｌｏｇｙ，２０２１，４４１：１０６６２２．

［２９］ 乔丹玉，郑进辉，鲁晗，等．面向不同环境背景的Ｌａｎｄｓａｔ影像水体提取方法适用性研究［Ｊ］．地球信息科学学报，２０２１，２３（４）：７１０－７２２．

［３０］ 吴啸龙，杨志强，龚云．球坐标多面函数空间数据插值方法研究［Ｊ］．测绘科学，２０１９，４４（３）：４７－５０，８５．

【责任编辑 许立新】