经验频率公式的比较与选择

慕平 慕星

摘 要：２０ 世纪初学者们研究提出了不同的经验频率公式，目前世界各国提出的经验频率公式多达数十种。采用不同的经验频率公式，直接影响后续的分析、计算及参数拟定等，这对设计洪水的估算结果有明显影响。通过对各类经验频率公式的比较，分析各经验频率公式的相对偏差，并用实测暴雨洪水系列初步验证经验频率公式的差别大小，得出洪水系列的最大洪水重现期误差最大，２０ ａ 一遇以下洪水重现期误差相对较小。为了尽可能地减小在设计洪水估算中所应用经验频率公式存在的理论方法误差，以及较短洪水系列中存在特大值、特小值而造成的原始资料误差，在实际应用时，需采用便于计算并趋近于无偏的经验频率公式。对相对较长的暴雨洪水系列，推荐选用经验频率公式的中值公式或数学期望公式进行频率（或重现期） 估计，建议将第一项（第二项）、末项的频率（或重现期）作为参考值。

关键词：设计洪水；经验频率；误差；中值公式；数学期望公式

中图分类号：Ｐ３３８ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２３．０７．００９

引用格式：慕平，慕星．经验频率公式的比较与选择［Ｊ］．人民黄河，２０２３，４５（７）：４８－５１，６７．

水文站的实测年最大暴雨洪水，每年必定会发生并且呈忽大忽小变化，该洪水大小值为随机变量。当实测洪水系列较长时，這些看似偶然的洪水呈现出一定的统计规律，可以用数理统计方法来加以分析。用数理统计法估算设计洪水存在３ 种误差，即原始资料误差、理论方法误差及运算误差［１］ 。原始资料误差主要表现为偶然误差及系列代表性问题；理论方法误差由理论研究不完善导致，目前只能列出有限的经验频率公式、频率曲线线型、参数估计、适线准则等供学者选用，但如何确切选用，国内外尚无明确定论；运算误差由解算方法不完善导致，可造成系统偏差。上述３种误差的大小直接影响设计洪水成果的可信度。目前，在任何科学技术领域，设计洪水的误差及不确定性问题是独一无二的［２］ 。

目前，世界各国提出的经验频率公式多达数十种，有的理论研究看似严密，实际应用却很难达到基本要求或假定，使问题更加复杂化，如资料系列较短而导致系列的代表性差或系列的均匀性差，极易在运算中将误差放大、传播，出现更大的系统偏差。采用不同的经验频率公式，直接影响后续的分析、计算及参数拟定等，这对设计洪水的估算结果有明显影响。为了尽可能地减小在设计洪水估算中所应用经验频率公式存在的理论方法误差，以及较短洪水系列中存在特大值、特小值而造成的原始资料误差，本文重点探讨如何选用经验频率公式及有效减小误差。

１．２ 各经验频率公式的相对偏差

由式（５）可以看出，当ａ 值为０～０．５ 时，其修正的经验频率值对系列的第一项、末项的频率值影响极大，虽可有效地避免较短系列末项出现频率为１００％的情况，但对第一项（即ｍ ＝１ 时）的频率值影响最大，之后随着ｍ 值的增大，其影响逐渐减小。

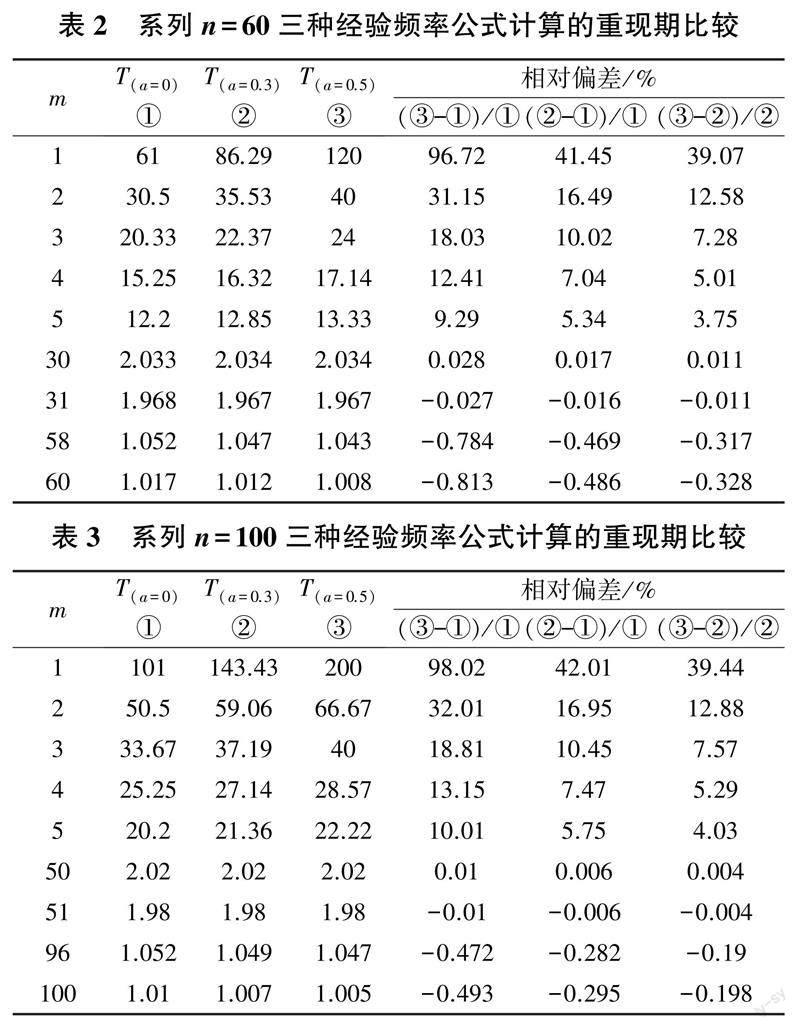
由于实测洪水系列长度较短（多数ｎ 小于１００），因此采用不同的修正经验频率公式对频率适线结果有相对偏大或偏小的影响。现列出了ｎ ＝ ６０、ｎ ＝ １００ 系列及ａ 取０、０．３、０．５ 时的系列重现期（见表２ 和表３）。可以看出，ａ 取０、０．３、０．５ 时系列第一项重现期相对偏差最大。以ｎ ＝１００ 为例，ａ 取０、０．３、０．５ 时，系列第一项重现期分别约为１０１、１４３、２００ ａ，第二项重现期相差略大，第二项之后相互间差别迅速减小，到中值项时的重现期相等，中值项以后ａ ＝ ０ 的重现期较大，ａ ＝ ０．５的重现期较小。

当ｎ ＝１００ 时，ａ ＝０．５ 与ａ ＝０ 对比，第五项以后其重现期相差在１０％以下，ａ ＝０ 时频率适线结果上端偏大、下端偏小，对洪水适线偏于安全；ａ ＝ ０．５ 时第一项的重现期是系列长度的２ 倍，适线结果相对偏小。当ｎ ＝６０ 时，ａ ＝０．３ 与ａ ＝ ０ 以及ａ ＝ ０．３ 与ａ ＝ ０．５ 对比，第三项以后其重现期相差均在１０％以下，这一情况表明，在２０ ａ 一遇以下，各经验频率公式得出的重现期的相对偏差很小，即在２０ ａ 一遇以下选哪种经验频率公式都可以，选ａ ＝０．３ 的频率适线结果介于取ａ ＝０和ａ ＝０．５ 之间。

１．３ 用实测系列初步验证经验频率公式的差别大小

１）系列的最大及次大洪水重现期。以上提到的各修正后的经验频率公式均依据相应的理论和经验，并均以ｎ 为无穷大为前提。但现实情况中多数系列ｎ为１００ 以下，其第一项、第二项的洪水值及重现期是极不稳定的，偶然得到的一个系列中的最大洪水值，经过一段时间后，有的被刷新，有的虽然没有被刷新，但次大洪水有可能被不断替换；随着时间的推移，最大洪水重现期在不断变化，有的系列最大值在８０ ａ 内不变，若在８０ ａ 之后的若干年又出现了更大洪水，则原来在８０ 多ａ内的第一大洪水，就变为第二大洪水。

可以设想当有一个近１ ０００ ａ 的洪水系列，若把这个相对的长系列分为ｋ 个短系列，每个短系列含有ｎ 项（６０ 或８０ 等）且相互独立。那么各个短系列的洪水可按自大而小的次序排列，则必有其中一个短系列的最大值是近１ ０００ ａ 的洪水系列中的最大值，而ｋ 个短系列中的最大值是不相同的，甚至差别较大。虽然各个短系列的第一项重现期按经验频率公式估算是相同的，但最大洪水值相差显著。

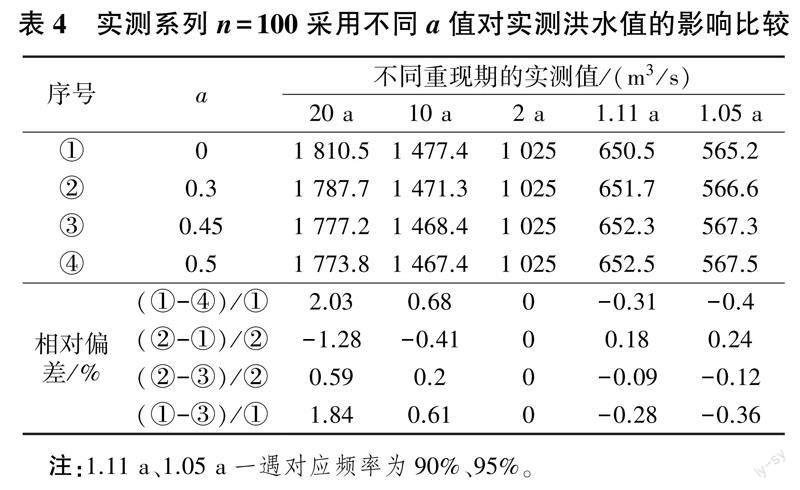
偶然得到某测站的ｎ 年较短的暴雨洪水系列，这其实与上述情况类似，其系列中的最大值与ｎ 年内这一特定时期暴雨洪水是否处于偏丰、偏枯等有着极大关系，系列中若出现较大值或特大值（特小值），这时采用上述任何经验频率公式估算出的第一项重现期均为不确定值（可以约为ｎ 年一遇，或ｎ ～２ｎ 年一遇，甚至超２ｎ 年一遇），虽然可以再进行人为处理，但很难处理到位，受主观影响较大，并直接影响到后续排频。２）２０ ａ 一遇以下洪水重现期。为了进一步验证当洪水系列相对较长时各经验频率公式在２０ ａ一遇以下重现期相对偏差很小，以及对实测的２０ ａ一遇暴雨洪水值的影响（即重现期横标的差异对实测洪水值纵标的影响），选取若干组６０～７０ ａ、８０～９０ ａ、１００～１２０ ａ及１６４ ａ、２４６ ａ 暴雨洪水系列，各系列Ｐ ＝５％（２０ ａ 一遇）的洪水值是Ｐ ＝９５％（１．０５ ａ 一遇）的洪水值的２．５倍至３６ 倍。当采用ａ ＝０ 与ａ ＝０．３ 及ａ ＝０ 与ａ ＝０．４５对比时，统计其各系列２０ ａ 一遇实测暴雨洪水值，平均偏差分别小于１．５％及２．０％，最大偏差分别小于３．５％及４．５％。经对比，其差值大小主要与各系列排序中２０ ａ 一遇上下两点数值差的大小有关。若这两点数值接近，用各种经验频率公式内插得到的实测２０ ａ一遇暴雨洪水值几乎相同；反之，则相差略大。由上述实例进一步表明，采用不同的ａ 值，用各种经验频率公式得到的各系列２０ ａ 一遇实测值偏差量级很小（用ａ ＝０ 得到的实测值略偏大，用ａ ＝ ０．４５ 得到的实测值略偏小），１０ ａ 一遇实测值相对偏差更小，中值的重现期及实测值相等，中值以下反之，用ａ ＝ ０ 得到的实测值略偏小，用ａ ＝０．４５ 得到的实测值略偏大（见表４）。

２ 经验频率公式的选择

经验频率公式的选取原则：尽可能减小设计洪水估算中所应用经验频率公式存在的理论方法误差，采用便于计算的并趋近于无偏的经验频率公式；减小较短系列中出现特大值、特小值而造成的原始资料误差。

２．１ 选用经验频率公式

目前，选用经验频率公式已集中在中值和均值公式，及采用以频率（Ｐｍ ）为特征值建立的横标经验频率公式或以变量（Ｘｍ ）为特征值建立的纵标经验频率公式（见表１）。由于频率分析是为了设计值（估计值）尽可能接近总体真值，因此把变量（Ｘｍ ）的分布中心对应的概率值作为第ｍ 项的绘点位置比取频率（Ｐｍ ）的分布中心更合理。

无偏经验频率公式与线型分布及特征值等有关。推导出的无偏经验频率公式，与各线型分布以及估算误差最大的偏态系数（ＣＳ）等有关，诸多问题交织在一起更加复杂，不便于应用。偏态系数（ＣＳ）对ａ 值有一定的影响，如克－闵分布的经验频率公式明确当ＣＳ ＞２ＣＶ、ａ ＝ ０．３ 时，相当于中值公式；当ＣＳ ＝ ２ＣＶ、ａ ＝ ０．４时，相当于皮尔逊Ⅲ型经验频率公式；当ＣＳ ＜２ＣＶ、ａ ＝０．５ 时，相当于海森公式。

经验频率公式是基于洪水系列各样本的出现具有等可能性且经验频率对称于中值建立起来的。从表１ 及现阶段的分析来看，无偏经验频率公式相应的ａ值介于０．３～０．５ 之间，其频率（或重现期）的大小在式（７）与式（８）计算结果之间。频率点绘常以均值、中值和众值３ 个特征值为分布中心，由数理统计可知，中值的特点是不像均值那样极易受特大或特小值的影响，它与排序位置有关，不受两边变数的影响。第二类公式中的中值公式与第一类公式的中值公式形式相同，且与总体分布无关，是一个稳健的经验频率公式，其频率值在均值和众值之间，为无偏估计值。由以上分析可知，经验频率的中值公式问题最少。

基于上述对比分析，特别经过１．３ 节的分析，说明对实测暴雨洪水系列采用不同经验频率公式计算出的２０ ａ 一遇以下暴雨洪水重现期相对偏差较小，并综合考虑资料代表性的不足及应用经验频率公式不能满足其基本条件或假定等情况，在实际应用时需采用便于计算的并趋近于无偏的经验频率公式形式，对相对较长的暴雨洪水系列，推荐选用式（６）或式（７），即中值公式或数学期望公式进行频率（或重现期）估计。

２．２ 对系列中特大值与特小值的处理

从以上经验频率公式的计算结果对比可以看出，虽然各经验频率公式均依据相应的理论、经验、分析及推理，但第一项频率（或重现期）相互间偏差最大。这一现象进一步表明，进行洪水系列排频，系列较短导致误差较大，特别是第一项频率（或重现期）。

各经验频率公式与系列中样本值大小、次序有关，但实际洪水系列较短，其变差各异，若在实测暴雨洪水系列中出现了不均匀情况，或出现较大值、特大值（或特小值），无论用任何经验频率公式计算其第一项、末项的频率（或重现期），其偏差都是不可预知的。对于特大值的超频，虽可再进行人为处理，但多数情况下很难处理到位，其误差大小受主观影响较大，并直接影响后续各项排频，可能造成更大程度的偏差。

其实，对于一个不均匀的短系列，把每个样本值按固定位置冠以一个频率（或重现期），这本身又加重了一层误差，表现为第一项误差最大，之后其误差逐渐减小，到中值项附近时其误差相对最小。

对实测洪水系列排频时，应遵循大数定律，不宜用抽样误差大的较短洪水系列，采用由严密理论推导的经验频率公式进行逐项排频。当实测洪水系列达到一定长度时，鉴于实测洪水系列中可能出现不均匀情况或出现特大值（特小值），各经验频率公式计算的第一项和第二项频率（或重现期）的相对偏差大、之后相互间差别迅速减小，实测洪水系列长度远远达不到大数定律所需的基本要求，建议由经验频率公式得出的第一项（第二项）、末项的频率（或重现期）仅作为占位排频，且只可作为分析估算的参考值。

３ 结论和建议

各种经验频率公式计算的样本系列第一项重现期相对偏差最大，第二项重现期相差略大，之后相互间差别迅速减小。当实测系列相对较长时，２０ ａ 一遇以下重现期相对偏差很小，即在２０ ａ 一遇以下选哪种经验频率公式都可以。鉴于偶然得到的实测暴雨洪水系列较短，在系列中常出现特大值或特小值、不均匀、资料代表性不足及应用公式条件不满足等问题，为有效减小设计洪水估算中所應用经验频率公式存在的理论方法误差，并尽可能避免将实测暴雨洪水系列中存在的误差进一步放大、传播的风险，在实际应用时需采用便于计算并趋近于无偏的经验频率公式。对于相对较长的暴雨洪水系列，推荐选用经验频率公式的中值公式或数学期望公式进行频率（或重现期）估计，建议将第一项（第二项）、末项的频率（或重现期）作为分析估算的参考值。

参考文献：

［１］ 刘光文．泛论水文计算误差［Ｊ］．水文，１９９２，１２（２）：１－１３．

［２］ 刘光文．水文频率计算评议［Ｊ］．水文，１９８６，６（３）：１０－１８．

［３］ 郭生练，叶守泽．论水文计算中的经验频率公式［Ｊ］．武汉水利电力学院学报，１９９２，２５（２）：３８－４５．

【责任编辑 张 帅】