明渠植物对沙波形态变化的影响研究

赵杰 孙雪岚 郝瑞霞 姚歌 张朝瑜 黄典晨

摘 要：沙波在自然河道中广泛存在，其对河床形态的变化起着不可忽视的作用。通过在玻璃水槽中采用有机玻璃棒模拟刚性挺水植物对沙波各种运动形态变化的影响，并引入ＭＩＫＥ２１ 水动力数值模型，从宏观与微观两个方面，研究沙波的波长、波宽、波高、波长波宽比、迎流面与背流面波长比等在水中植物影响下的变化现象，探究河道泥沙的群体运动机制，为自然河道中泥沙的治理提供一定的借鉴。结果表明，在挺水植株对水流流态变化的影响下，沙波的波长、波宽、波高沿程形态变化显著，尤其在植株绕流影响下，泥沙颗粒在植株两侧运动速度增大，呈现冲刷的态势，沙波也随之出现复杂的运动形态，植树前后上游沙波形态亦有显著差异。

关键词：沙波；植物；流场；ＭＩＫＥ２１

中图分类号：ＴＶ８３ 文献标志码：Ａ ｄｏｉ：１０．３９６９／ ｊ．ｉｓｓｎ．１０００－１３７９．２０２３．０７．００８

引用格式：赵杰，孙雪岚，郝瑞霞，等．明渠植物对沙波形态变化的影响研究［Ｊ］．人民黄河，２０２３，４５（７）：４２－４７，６７．

随着我国国民经济的不断发展，河流在人民日常生活和国家经济建设中扮演着越来越重要的角色，尤其是在居民生活供水与农业灌溉用水方面，更是起着不可忽视的作用。系统研究自然河道中推移质泥沙的运动状况，准确掌握河床冲淤演变规律是充分发挥河流综合效益的前提条件。沙波形态变化是水动力、泥沙性质、各种边界条件共同作用的结果［１］ ，是河床形态变化的重要表现形式［２］ 。沙波的动态变化经常影响着人类的各类活动，例如航运和近岸工程建设等，尤其是对浅水区的航运影响显著；同时对河底设施构成安全隐患，如取水工程等。因此，研究沙波形态变化对水上航运、设施建设等均有重要的意义。

随着水流的运动，推移质颗粒群体在宏观上做各种不同形式的运动，床面形态也随着输沙强度的不同而实时改变［３］ 。沙波的形成发展影响着河床阻力及推移质输沙率等，对河道的自然演变有着重要的影响［４］ 。关于沙波的形成机制，Ｃｏｒｎｉｓｈ［５］ 认为初始沙波的形成是泥沙冲淤的结果，其中沙波横向发展速度主要受近床水流影响。Ｄａｍｇａａｒｄ 等［６］ 分析了泥沙非均匀度对沙波形态的影响，认为沙波波长、波高随水流强度的变化不受泥沙非均匀度的影响。Ｗｅｒｎｅｒ 等［７］ 歸纳了沙波波长随时间的变化规律。沙波运动规律与多种因素存在着密切关系。Ｃｏｌｅｍａｎ 等［８］ 基于水槽试验数据，建立了沙波波速、波高与推移质输沙率之间的函数关系。Ｒａｕｄｋｉｖｉ［９］ 通过数值试验得出沙波是泥沙颗粒在各种因素共同作用下的宏观表现，并进一步发现沙质推移质输沙率与沙波的波高成负相关关系，河道中植物的阻力作用直接、间接影响着沙波的形态变化，尤其是对水流流态的影响，间接影响了沙波的运动变化规律。Ｄｕｎｎ 等［１０］ 在矩形渠道中对淹没的刚性与柔性圆棒进行试验研究，发现水流阻力随植被密度的增大而增大。张原锋等［１１］ 利用床面形态控制数及床面形态判别方法，研究发现当流量逐渐增大时，床面形态逐渐由沙垄向过渡、动平整方向发展。

在天然河道中，外界环境条件复杂，不能保证沙波形态是在观测到的水流条件下形成的，故研究采用室内玻璃水槽试验方法，以基本确保沙波形态与当前水流条件的一致性。在植物对沙波运动形态的影响领域，前人的研究甚少，本文基于推移质模型沙运动的试验数据，分析了植物种植前后，水槽沿程的沙波波高、波长、波宽等的变化情况，并应用ＭＩＫＥ２１ 软件对植被影响下的水流流态进行了数值模拟计算，分别从微观与宏观两方面定性、定量地研究刚性植物对沙波形态变化的影响及其变化规律，进而比较分析植物种植前后沙波形态的差异，以期深入理解河床推移质运动的特点与规律，完善动床河道的泥沙治理理论与方法。

１ 试验简介

１．１ 试验设备

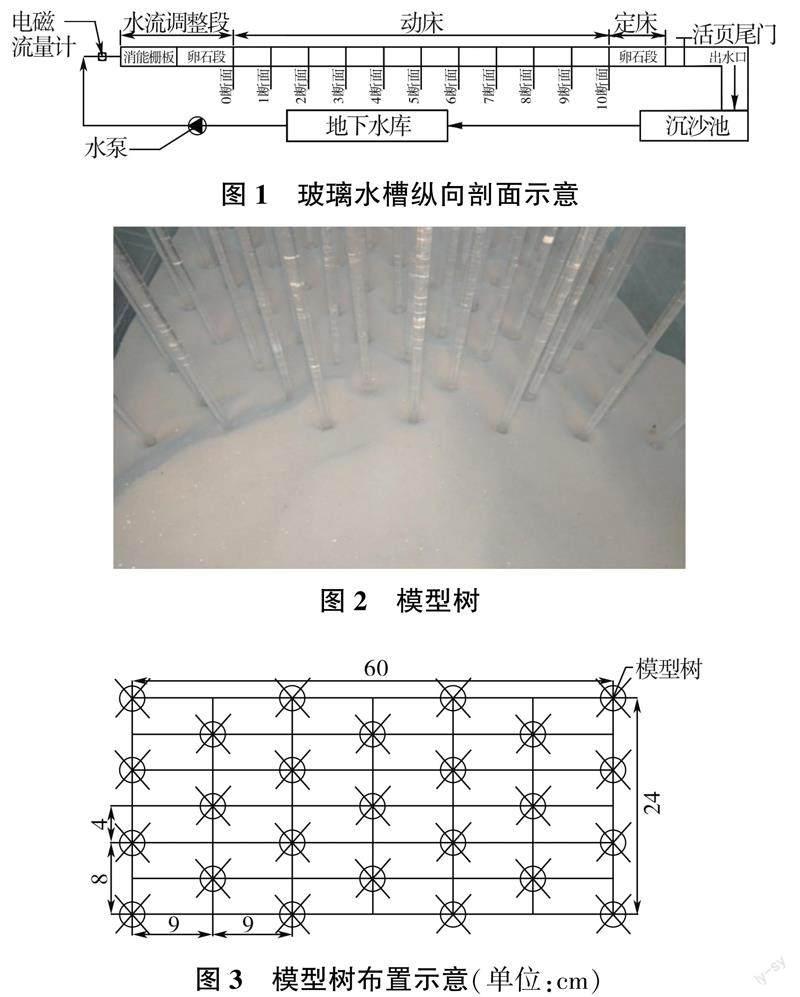
本试验是在太原理工大学水利科学与工程学院水工实验室的玻璃水槽内进行的（设备布置见图１），水槽长１２ ｍ、宽０．４ ｍ、高０．５ ｍ，玻璃水槽底部平整度小于０．５ ｍｍ。水槽模型试验用水由循环供水系统供给，能保证水流状态为恒定流。整个循环供水系统由变频控制水泵提供所需流量，电磁流量计观测实时流量。槽首设有消能栅板，用于稳定水流；水槽末端设有可调节的活页式尾门，垂直于出水口处设有一拦沙筛，水流经尾门后穿过拦沙筛跌入水道。

水槽上设有可活动测针架，水槽顶部有带刻度的轨道，可供测针架移动与读取所测断面的位置。在玻璃水槽底部设有自动升降螺杆，可用于调节水槽的坡度。沿水槽纵向自进口起设置了１０ 个量测断面，断面间距为１．０ ｍ，水槽轨道刻度零点所在的断面记为０ 断面，其余断面依次编号（见图１）。

１．２ 试验方案

试验采用中值粒径ｄ５０ ＝０．３４ ｍｍ 的非均匀塑料沙作为推移质模型沙，塑料沙在目前河工模型试验中运用较为广泛，密度约为１ ０５０ ｋｇ／ ｍ３，呈白色半透明状。塑料沙为憎水型轻质沙，在水中的物理、力学性质都较为稳定，且颗粒间一般不存在黏结现象。水槽底部铺约５ ｃｍ 厚的模型沙，试验过程中根据输沙率在水槽首部加沙。

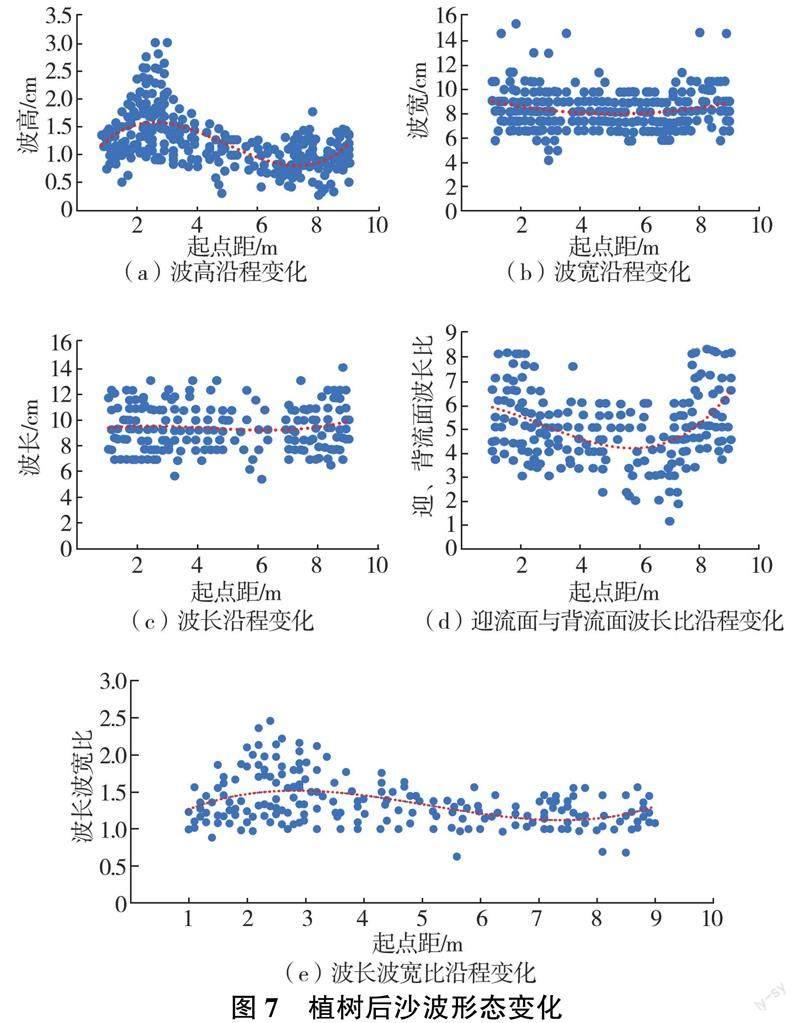
为了较真实地模拟刚性挺水植物对水沙运动的影响［１２］ ，同时考虑到树木的阻力相似，本试验采用有机玻璃棒模拟自然茎秆状的挺水植物（见图２），有机玻璃棒高２６ ｃｍ、直径４ ｍｍ。试验采用网格结构来固定有机玻璃（模型树），试验时将模型树固定在网格的圆形孔内。模型树布置采用行列交错方式，其中行距为９ ｃｍ、株距为８ ｃｍ，共７ 排，植物群长６０ ｃｍ、宽２４ｃｍ，共２５ 棵，种植密度为１７４ 棵／ ｍ２，模型树布置示意如图３ 所示。为避免平整床面因初始流量过大冲刷泥沙而破坏底床，试验中水槽流量逐步调节，最终稳定流量为７．６９ Ｌ／ ｓ，采用沙莫夫公式计算得泥沙颗粒起动流速为０．０４１ ｍ／ ｓ。

１．２．２ 试验测试手段

本试验通过可活动式测针测读水位、沙波各部位的水深等，测量精度达０．１ ｍｍ。采用多普勒流速仪测量流速，基于声学多普勒原理测量水体中粒子的运动速度来代表水体运动速度，测量精度达０．００１ ｍ／ ｓ。水槽流量通过电磁流量计测量，测量原理是基于法拉第电磁感应定律，测量精度可达０．０１ ｍ３ ／ ｈ。

２ 试验现象及分析

２．１ 植树前沙波沿程变化

大部分试验数据表明，当河槽底部比较平坦时，沙波的波高、波长等都比较均匀。本试验选取了多组形态较为明显的沙波进行量测，如图５ 所示。受玻璃水槽边界的影响，部分沙波失真，所以数据较为离散，本文选取数目较多的沙波来分析其变化的总趋势。植树前沙波各种形态沿程变化规律见图６，其中红线为拟合的整体趋势线。

从图６ 中趋势线可以看出沙波的波长、波宽均沿程逐渐增大，主要原因是玻璃水槽中水流流速沿程逐渐加快。相比之下，波长波宽比却沿程逐渐减小，说明波长沿程变化幅度大于波宽的变化幅度。迎流面与背流面波长比也在逐渐增大，说明迎流面波长增长幅度大于背流面波长的增长幅度。试验中波高沿程下降，其趋势线斜率比其他指标趋势线斜率大，直到水槽２．３５ ｍ刻度处，河床仍无明显起伏状态。大部分试验表明，沙波的波高随水流流速的加快而增大，当超过某一临界值后，由于水流流速过快，冲刷加剧，沙波波高反而逐渐减小，直至消亡，说明试验中虽然水流流速在水槽中沿程加快，但是水流初始速度已经超过波高增加的临界值，故研究中植树前的沙波波高呈现逐渐减小的趋势。从图６ 中可以看出沙波的各种形态均随水槽长度的增加而逐渐变化，直到约２．５ ｍ 处，沙波形态逐渐消亡。从上述分析可以看出，在玻璃水槽中未植树前，沙波形态沿程变化的趋势均具有一定的规律性，且基本为较单一的线性变化。

２．２ 植树后沙波形态沿程变化

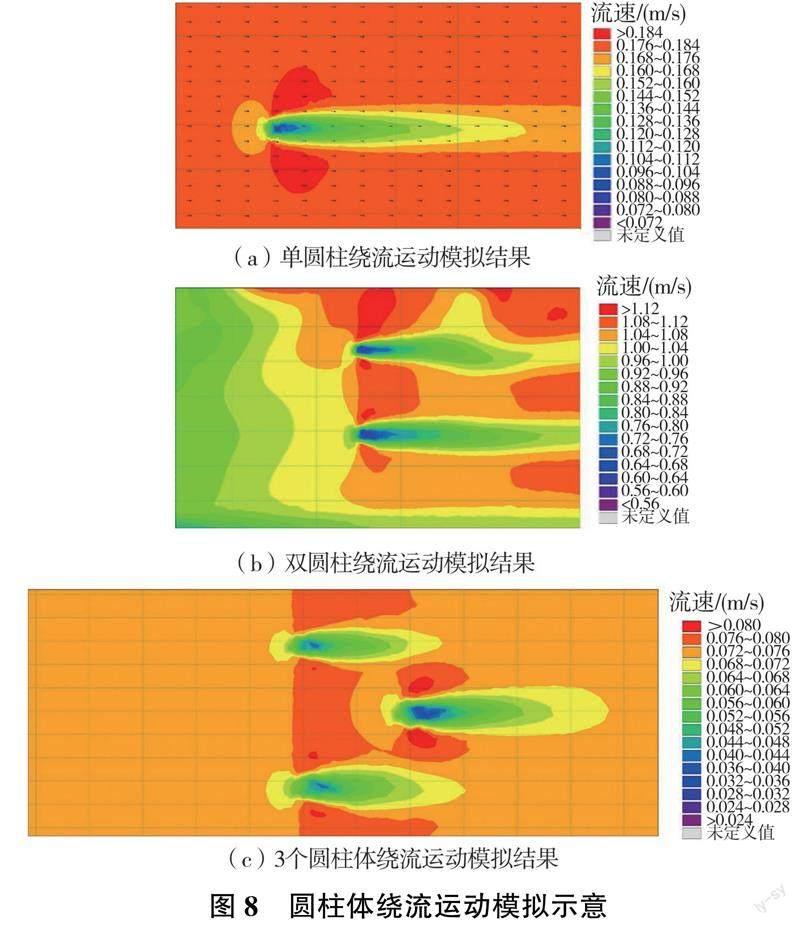
水槽中植树后沙波形态的沿程变化有较明显的规律性，如图７ 所示虚线为拟合的整体变化趋势线。图７（ａ）为沙波波高沿程变化趋势图，沙波波高在植株群上游呈现先增大后逐渐减小的趋势，而流速是沿程逐渐递减的。这是因为沙波波高随流速的增大而增大，但是当流速超过一定值时，水流的冲刷作用又会使沙波波高逐渐变小，所以在流速逐渐变小过程中，靠近进口段水流流速较大，对波高有冲刷作用，而流速沿程减小后冲刷作用减弱，推移质泥沙颗粒被水流带到波峰较多，波高高度增大，之后水流流速继续变小，泥沙颗粒运动变缓，波峰高度逐渐减小。图７（ｂ）为沙波波宽沿程变化趋势图，从趋势线可以看出沙波波宽沿程变化幅度较小，但仍然呈现逐渐减小的趋势，水流流动变缓，水流能量减弱，沙波波宽变小。图７（ｃ）为沙波波长沿程变化趋势图，从图中的变化趋势线可以看出在植株群上游波长整体趋势变化不大，但有轻微减小，这是因为植株群对水流有一定的阻滞作用，在植株群上游出现壅水，水流流速沿程逐渐减小，沙波波长随流速的减小亦呈现逐渐减小的趋势，由于波峰处水流流速减小，波峰泥沙运动速度变慢，部分泥沙沉降，宏观上表现为波峰运动被阻滞，速度变慢，沙波背流面向前推进亦变缓，沙波迎流面流速大于波峰处流速，泥沙运动速度也同样大于波峰处泥沙的运动速度，故波长在宏观上表现为变短。相反，波峰处流速大于迎流面的流速时，波长在宏观上表现为变长。图７（ｄ）为迎流面与背流面波长之比沿程变化情况，从趋势线可以看出，在植株群上游波長比沿程呈减小趋势，至植株群前变为最小，即背流面波长变化幅度小于迎流面，说明背流面淤积程度高于迎流面的冲刷程度。图７（ｅ）为波长波宽比沿程变化趋势图，趋势线表明波长波宽比在植株群上游先变大后逐渐减小，与沙波波高沿程变化趋势类似。波长波宽比沿程变化亦有一个临界值。波长、波宽随流速增大逐渐变大，说明同一沙波的波长沿程变化幅度先大于波宽的变化幅度，之后又逐渐小于波宽的变化幅度，除去一些特殊点，波长波宽比始终大于１，即波长始终大于等于波宽。从图７（ｅ）中可以看出在植株群下游的沙波数量突然变少，这是因为植株群下游水深大幅度减小，流速大幅度增大，沙波形态逐渐消亡，一段距离后水深逐渐恢复至植树前的水深，流速亦逐渐减小，河床底部再次产生沙波形态。

２．３ 基于ＭＩＫＥ２１ 的有机玻璃棒绕流运动分析

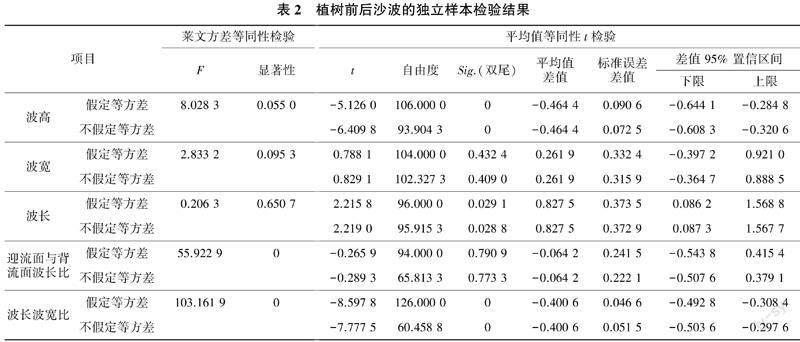
物理试验对水槽流场的观测难以保证连续性，且观测结果受限于各种外界条件的影响，无法得到一个较准确完整的水槽流速分布及变化，故此处基于ＭＩＫＥ２１ 软件对水槽水流的流场变化进行水动力数值模拟，可以得到更加直观的流场分布，更全面地分析模型树周围的流场变化，为进一步研究沙波的模拟计算做基础。ＭＩＫＥ２１ 是一个专业的工程软件包，在平面二维自由表面流数值模拟方面具有强大的功能。为了更全面直观地研究水槽中的流场变化， 本文基于ＭＩＫＥ２１ 水动力模块（ＨＤ）对有机玻璃棒的绕流运动形态进行仿真模拟，从微观角度更加细致地去观察水流流态在圆棒阻力作用下的完整变化。本模拟试验采用圆柱体模拟刚性挺水植株，并分别设计了单圆柱体、并排双圆柱体、３ 个圆柱体３ 种水流绕流运动的数值模拟方案（模拟结果如图８ 所示，不同颜色及其颜色的深浅程度代表不同的流速范围）。

结合现有的研究成果，从流体力学角度分析，每一棵模型树实际上就是一个边界条件极为复杂的柱体。圆柱体形体阻力、阻水范围与拖曳力的存在，使有机玻璃棒迎流面一段范围的流速降低，从图８（ａ）中可以看出，有机玻璃棒周围流速分布为层式分布，类似蜡烛火焰的分布形式。最内侧即紧贴圆柱体一层为蓝色层，距离圆柱体越近、颜色越深、速度越小，其中颜色最深处流速小于０．０９６ ｍ／ ｓ。整个圆柱体周围的流速分布呈拖曳状。在顺水流方向，圆柱体两侧各有一半圆形红色流速区，流速大于等于０．１７６ ｍ／ ｓ。结合已有试验结果可知，水流在圆柱体的前驻点速度为０，水流沿圆柱体两侧流动，水流压力在圆柱体前半部分慢慢减小，流速逐渐增大到最大值，故圆柱体两侧有红色流速区，并大于来水流速。随着水流向圆柱体后半部分流动，水流压力慢慢增大，流速逐渐减小，当水流到达圆柱体背流面驻点时，流速重新变为０。

圆柱体周围泥沙颗粒运动随流态变化而变化，泥沙颗粒在圆柱体周围有部分沉积，但由于流速减少范围较小，且考虑到有机玻璃棒在水中来回振动作用，实际中植株群前流速并不为０，植株群前、后流速差异并不十分显著，因此并未观察到明显的泥沙沉积现象。由于模型树两侧的流速增大，因此迎流面波长逐渐增大。沙波运动到模型树前时，受树形阻力作用与水流作用，波宽增长趋势明显。图７（ｅ）中显示波长波宽比在植株群内逐渐减小，这是因为波宽变化幅度大于波长的变化幅度，但植株群后的冲刷使波长波宽比又突然增大。圆柱体两侧流速加快，泥沙颗粒起动数量变多，运动速度加快，有冲刷趋势，故沙波波高有降低趋势。

当２ 个圆柱体并排同时存在于水流中时，如图８（ｂ）所示，有２ 个拖曳状流速分布区并行存在，２ 个圆柱体中间流速增大的范围变大，但流速增大幅度变小，表明由于两边水流的对冲，消耗了一部分动能，流速增大的速度变缓，但速度增大范围较单圆柱体整体变大，对沙波影响范围亦增大。

当３ 个圆柱体同时存在于水流中时，如图８（ｃ）所示，由于第二排圆柱体的阻力作用，第一排平行放置的２ 个圆柱体间流速增大范围较图８（ｂ）变小。同时，受第一排两个圆柱体背流面流速变化的影响，第二排圆柱体两侧流速增大范围亦变小。此时沙波变化较复杂，整体波高呈减小趋势，波宽迅速增大。

从图７ 中可看出，植株群范围内波长逐渐增加，迎流面与背流面波长比逐渐增大，相比较波长波宽比的变化不是很显著，并有减小的趋势。结合图８（ｃ）流速分布图，从流速解释该变化现象，前后排圆柱体周围流速整体偏大，故水流可带起更多泥沙颗粒，整体偏冲刷态势。模型树形体阻力等的存在，使波宽、波长增大的同时波高逐渐减小，但由于本试验中模型树密度较小，因此沙波并未消失。

考虑到有机玻璃棒在水中来回振动，植株群前流速并不为０，植株群前、后流速差异并不显著，因此圆柱绕流形成的复杂条件导致沙波波峰高度并不十分显著。但是模型树周围的流速增大，导致迎流面波长逐渐增大。沙波运动到模型树前时，受模型树的树形阻力作用与水流作用，波宽增长速度变快。图７（ｅ）中显示波长波宽比在植株群内逐渐减小，这是因为波宽变化幅度大于波长变化幅度，但植株群后的冲刷使波长波宽比又突然增大。

２．４ 植树前后对比分析

采用ｓｐｓｓ 统计软件对玻璃水槽中植树前后０ ～３ ｍ之间的沙波形态数据进行独立样本ｔ 检验分析，分别选取植树前４５ 组沙波与植树后５６ 组沙波，判断植树条件变化对上游沙波形态变化的影响程度，结果见表１、表２。

表１ 是植树前后沙波波高、波宽、波长、迎流面与背流面波长比、波长波宽比试验结果统计。可以看出，植树前后沙波数目相差不多，即植树对上游沙波数目影响并不显著。波宽、波长的平均值植树前均略大于植树后；与之相反，波高与波长波宽比植树后均显著大于植树前，迎流面与背流面波长比则基本相同。

从标准偏差来看，波高、波宽、迎流面与背流面波长比、波长波宽比均是植树后显著大于植树前，说明植树后数据变得更加紊乱，即模型树的存在使沙波多种形态数据的离散程度变大。但是波长的标准偏差在植树后略大于植树前，说明植树后波长数据离散程度变化不大。

波高、波宽、波长的莱文方差等同性检验的显著性均大于０．０５，即判断植树前后两总体为方差齐性，选择假定等方差ｔ 检验，迎流面与背流面波长比、波长波宽比的莱文方差等同性检验的显著性均小于０．０５，即判断植树前后两总体为方差非齐性，选择服从修正自由度的不假定等方差ｔ 检验。

波高、波长波宽比的Ｓｉｇ．（双尾）均小于０．０１，说明这两种沙波形态在植树前后有显著差异。波宽、波长、迎流面与背流面波长比的Ｓｉｇ．（双尾）均大于０．０１，说明植树前后无显著差异。

从图６ 可以看出，植树前沙波集中出现在０ ～３．０ ｍ范围内，而植树后则沿程均出现沙波形态，说明植树对河床沙波影响显著。在自然河流内种植植物后，应该重视河床沙波形态的变化，进而对河道自然条件下河床冲淤演变规律进行趋势预测，对于合理安排河流两岸经济技术活动，保证拟建设工程安全并发挥应有的效益至关重要。

结合表１ 的数据，可判断出植树对沙波形态的影响。植树条件的变化对沙波波宽、波长、迎流面与背流面波长比无显著影响。但是，上游波高与波长波宽比受植树条件影响较大，植树后波高与波长波宽比显著增加，沙波轮廓更加明显，河床形态更加复杂。

３ 结论

１）沙波的各项要素受植树情况影響较大，沿程变化具有一定的规律性，从变化趋势上看各有区别。

２）ＭＩＫＥ２１ 水动力模型的模拟结果表明，在植株群范围内，水流条件复杂，沙波受植株形体阻力与阻力范围影响显著。

３）独立样本ｔ 检验表明，植树后波高、波长波宽比显著增大，沙波轮廓更加明显。

４）泥沙群体运动是一个非常复杂的问题，目前研究还很不充分，尤其是放入植株群后使问题更加复杂。进行更深入的研究，除需要用先进的测量手段、仪器和大量的模型试验外，还需要合理选择参数并积累丰富可靠的实测资料。

５）本文未对沙波形态变化进行数值模拟分析，今后将进一步研究，结合更多的试验数据，总结沙波变化规律，得出相应的计算公式和适用的计算方法，结合计算机技术解决实际工程中的泥沙问题。

参考文献：

［１］ 钱宁，万兆惠．泥沙运动力学［>Ｍ］．北京：科学出版社，１９８３：１４０－１８２．

［２］ 段文忠．沙波尺度和运动速度与水力泥沙因素的关系［Ｊ］．武汉水利电力学院学报，１９８８，２１（４）：６６－７２．

［３］ 惠二青，江春波，潘应旺．植被覆盖的河道水流纵向流速垂向分布［Ｊ］．清华大学学报（自然科学版），２００９，４９（６）：８３４－８３７．

［４］ 高昂．沙波面水沙运动特性及沙波演化规律试验研究［Ｄ］．郑州：华北水利水电大学，２０１６：２３－４８．

［５］ ＣＯＲＮＩＳＨ Ｖ．Ｏｎ Ｓａｎｄ⁃Ｗａｖｅｓ ｉｎ Ｔｉｄａｌ Ｃｕｒｒｅｎｔｓ［Ｊ］．Ｔｈｅ Ｇｅｏ⁃ｇｒａｐｈｉｃａｌ Ｊｏｕｒａｌ，１９９１，１８（２）：１７０－２００．

［６］ ＤＡＭＧＡＡＲＤ Ｊ Ｓ，ＳＯＵＬＳＢＹ Ｒ，ＰＥＥＴ Ａ，ｅｔ ａｌ．Ｓａｎｄ Ｔｒａｎｓｐｏｒｔｏｎ Ｓｔｅｅｐｌｙ Ｓｌｏｐｉｎｇ Ｐｌａｎｅ ａｎｄ Ｒｉｐｐｌｅｄ Ｂｅｄ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆＨｙｄｒｏｌｏｇｉｃ Ｅｎｇｉｎｅｅｒｉｎｇ，２００３，１２９（９）：７０６－７１９．

［７］ ＷＥＲＮＥＲ Ｂ，ＫＯＣＵＲＥＫ Ｇ．Ｂｅｄｆｏｒｍ Ｓｐａｃｉｎｇ ｆｒｏｍ Ｄｅｆｅｃｔ Ｄｙ⁃ｎａｍｉｃｓ［Ｊ］．Ｇｅｏｌｏｇｙ，１９９９，２７（８）：７２７－７３０．

［８］ ＣＯＬＥＭＡＮ Ｓ Ｅ，ＭＥＬＶＩＬＬＥ Ｂ Ｗ．Ｂｅｄ⁃Ｆｏｒｍ Ｄｅｖｅｌｏｐｍｅｎｔ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙｄｒａｕｌｉｃ Ｅｎｇｉｎｅｅｒｉｎｇ，１９９４，１２０（４）：５４４－５６０．

［９］ ＲＡＵＤＫＩＶＩ Ａ Ｊ．Ｒｉｐｐｌｅｓｏｎ Ｓｔｒｅａｍ Ｂｅｄ ［Ｊ］．Ｊｏｕｒｎａｌ ｏｆ Ｈｙ⁃Ｄｒａｕｌｉｃ Ｅｎｇｉｎｅｅｒｉｎｇ，１９９７，１２３（１）：５８－６４．

［１０］ ＤＵＮＮ Ｃ，ＬＯＰＥＺ Ｆ，ＧＡＲＣＩＡ Ｍ．Ｍｅａｎ Ｆｌｏｗ ａｎｄ Ｔｕｒｂｕｌｅｎｃｅｉｎ ａ Ｌａｂｏｒａｔｏｒｙ Ｃｈａｎｎｅｌ ｗｉｔｈ Ｓｉｍｕｌａｔｅｄ Ｖｅｇｅｔａｔｉｏｎ［Ｒ］．Ｃｈｉ⁃ｃａｇｏ：Ｄｅｐｔ ｏｆ Ｃｉｖｉｌ Ｅｎｇｒｇ，Ｕｎｉｖ ｏｆ Ｉｌｌｉｎｏｉｓ ａｔ Ｕｒｂａｎａ⁃Ｃｈａｍ⁃ｐａｉｇｎ，１９９６：１９－１０５．

［１１］ 张原锋，王平．黄河下游游荡型河段床面形态变化特征［Ｊ］．人民黄河，２０１８，４０（８）：８－１１．

［１２］ 程年生．植被对明渠水流及泥沙运动的影响［Ｊ］．水力发电学报，２０１８，３７（９）：１－７．

【责任编辑 简 群】