基于多变量公钥密码构建热钱包安全保护方案
朱飑凯,张禧龙,刘三满,宋 杰,郭 春,赵菊敏
(1.山西警察学院 网络安全保卫系,山西太原 030401;2.智能警务四川省重点实验室,四川泸州 646000;3.太原理工大学 信息与计算机学院,山西晋中 030600)
区块链中心交易所或Dapp 钱包主要对用户的私钥进行保密性监管,但大多数情况下会将私钥保存在服务器上,所以平台采取开源方案只会对服务器安全、平台数据安全、用户资产安全起到一定作用。
在实际区块链交易中,交易过程安全、热钱包保护是亟待发现、研究的。攻击者往往会通过利用多项智能合约漏洞以及窃取私钥复制热钱包的方法来获取热钱包中的虚拟货币。同时量子计算技术高速发展、抗量子密码研究步伐加快,区块链加密技术却仍在采用第一代公钥密码算法来保证数据库的安全性,且RSA 算法曾被爆出可进行多种攻击破解,因此区块链热钱包保密算法更新迫在眉睫。
基于对现存热钱包安全性问题的综合研判,文中提出了一种对热钱包内私钥应用多变量公钥密码加密的热钱包保护方案,以应对攻击者破译私钥、复制钱包窃取虚拟货币,及防止热钱包管理公司非法提取用户虚拟货币等问题。该模型利用抗量子技术,使用多变量公钥加密,确保私钥的保密性。在热钱包中仅仅存储的是私钥的密文,并不对私钥进行直接保存,极大优化了热钱包在实际中的使用体验。
1 方案简述
1.1 方案对钱包进行优化及提高安全等级
1)针对热钱包服务器存储私钥遭受恶意入侵的问题,提出了基础模型架构:服务器并不对私钥进行直接保存,而是保存私钥的密文。增加热钱包的加密模块,使用该模块对私钥进行多变量公钥密码加密,形成密文后再进行保存[1]。
2)针对目前RSA 和SM2 椭圆曲线数字签名难以抵抗量子技术的问题,以及大整数因式分解、离散对数可逆解等易窃密行为,文中提出了一种多变量公钥加密结合SM2 椭圆曲线数字签名的多重加密架构。经研究发现,多变量公钥加密可有效对抗量子计算攻击,即使攻击者对钱包外部进行暴力破解,也仅只得到私钥的密文,从而实现对私钥的保护,从理论上大大提升了安全性[2]。
3)针对现行的用户间资产交易主要通过用户输入密钥进行链上签名验证,在提高安全性之后,可以将部分业务移交给热钱包交易平台,大大减轻了用户的操作负担,简化了转账、交易或融资流程,使用户的操作更加简洁有效[3]。
1.2 方案具体框架
私钥由随机数生成器随机生成,是决定用户账号中虚拟货币所有权的关键。文中方案将私钥作为明文1,通过多变量公钥密码算法进行加密,形成密文1,在此期间将会生成私钥1 以及公钥1。私钥1由用户保存,再将密文1 保存在热钱包中。形成的密文1 作为SM2 椭圆曲线数字签名的明文生成公钥以及地址,公钥公开在区块链上。在使用钱包的过程中,钱包只保存私钥经过多变量公钥密码加密后的密文,在用户需要进行转账时,自行输入私钥进行交易的确认。热钱包私钥加密流程如图1 所示。
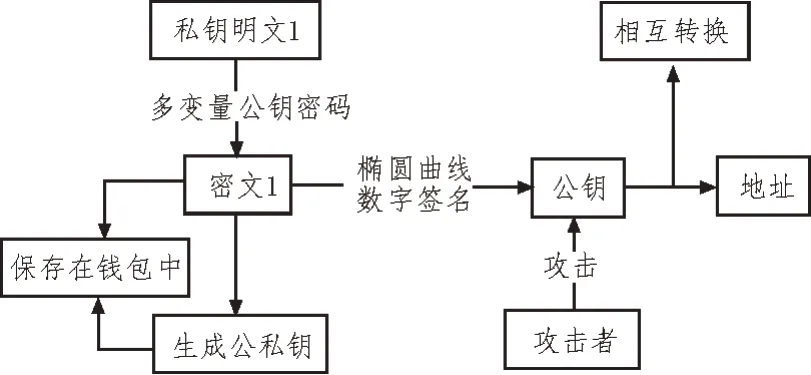
图1 热钱包私钥加密流程
私钥即明文1,定义为(x1,x2,x3,x4,…,xC),公钥1即密文1,定义为(y1,y2,y3,y4,…,yB)。
多变量公钥密码加密流程如下[4]:
假设A是一个有限性的值域,B、C取值为正整数:
其中,定义Z和T是AB和随机选取的可逆仿射变换。定义映射G为一个值在AB和之间可求逆元的非线性映射,一般为二次函数。定义$为多个映射进行合成。定义是AB在上的映射,可以表示为A上的B个C元多项式[5]。
Qi作为A上的n元多项式,其最高次和Z的次数相等。
此时Z作为线性变换,T作为平移变换,G可以使用Sigmiod 函数进行计算[6]:
应用于多项式公钥密码时,将定义为公钥1,即(q1,q2,q3,q4,…,qB),私钥是Z和T两个可仿射变换以及D[7]。
加密过程如下:
将私钥作为明文消息(x1,x2,x3,x4,…xC),经过G加密之后,得到密文1 (y1,y2,y3,y4,…,yB),即对所有i=1,2,…,B的取值有:
解密过程如下:
通过私钥1 计算G的逆元g,对应即可以求出所有Qi的逆元qi,输入公钥1即密文1(y1,y2,y3,y4,…,yB),就可以得到明文即公钥1,即对所有i=1,2,…,C的取值有:
1.3 模型优势
该模型从理论上一方面可以防止攻击者对SM2椭圆曲线数字签名[9]破解之后,直接获取私钥的可能。假设攻击者对热钱包成功破解,获取到的只是私钥经过多变量加密后的密文,且多变量公钥密码可以有效防御量子计算机暴力破译及抗量子计算,增加了一定的安全性;另一方面,在热钱包中存储的只是密文没有直接对私钥进行存储,有效解决了钱包公司自身不安全或者有不法行为的问题。该模型主要提出了一种新式热钱包架构的想法,在钱包中加入对私钥进行加密的模块,较好地优化了热钱包安全算法[10]。
2 实现与结果分析
2.1 加密平台设计应用
2.1.1 测试系统设计
前文对应用多变量公钥密码算法的私钥加密过程的理论部分进行了描述,同时,对应用SM2 椭圆曲线数字签名[11]将密文1 加密的算法结构进行了细致介绍,通过构建实验对之前涉及到的算法进行实现。文中实验整体实现过程分为四大模块:搭建平台测试环境、多变量公钥加密算法实现、SM2 椭圆曲线数字签名模块改进、通过构建创世区块搭建私有链测试结果[12]。
2.1.2 环境配置
测试方案的硬件为计算机,具体配置有:
处理器为Intel(R) Core(TM) i5-9300H CPU@2.40 GHz,机带RAM 为8.00 GB,操作系统为Window 10。
2.1.3 测试系统结果
测试平台以GO 语言为基础,应用Geth 客户端搭建私有链,进一步验证实验结果的可实现性及对该方案的实际性评估。测试平台搭建主要分为五大模块:①GO 语言、Geth 环境部署;②私有链账户注册;③以太坊钱包创建;④创世区块创建;⑤节点创建。
GO 语言部署结果如图2 所示。该模块主要测试平台构建相应的语言及以太坊节点,为与区块链进行通信交易,需使用区块链客户端节点,与其他客户端节点建立P2P通信信道,用于签署和广播交易信息[13]。

图2 GO语言环境部署
创世区块创建结果如图3 所示。因为实验测试需要在区块链中进行,所以首先要搭建起一条合适的私有链,通过在私有链中创建节点进行交易来模拟正式公链中的交易流程。

图3 创世区块创建
节点创建结果如图4所示。启动节点成功后,进入Geth 的命令行模式,输入命令personal.newAccount()后,会提示输入账号密码,并确认,最后会显示一个新生成的账号。

图4 新节点账号生成
2.2 加密模块实现
2.2.1 基于多变量公钥加密算法测试
下面主要对前文所提出的新型多变量公钥加密算法应用jupyter 进行实现,将私钥分为两组,分别进行随机仿射加密,并应用SM2椭圆曲线数字签名形成最终密文。环境配置同2.1.2。
该实验对随机数生成器生成的一串64 字节明文:0926518763557286729845266738580987636263 554871098327837652908736,经过多变量公钥加密后生成密文。加密测试结果如图5 所示。

图5 私钥经多变量公钥加密后密文
2.2.2 SM2椭圆曲线数字签名
文中方案提出将个人私钥经过多变量公钥密码算法加密之后生成的密文1 存储在热钱包中,密文1不会直接对外,而是在将该密文1 进行SM2 椭圆曲线数字签名之后作为公钥发布在公有链上[14],以下是具体实验测试:
环境配置同2.1.2。该实验加密一串64字节明文:09265187635572867298452667385809876362635548 71098327837652908736,经过SM2 椭圆曲线数字加密后生成密文。
测试结果如图6、图7 所示,图6 为密文,图7 为生成的公钥和私钥。

图6 密文

图7 公私钥
2.3 对比安全性分析
文中成功实现了对私钥进行分组后利用随机可逆仿射变换求出密文1,再利用SM2 椭圆曲线数字签名形成最终密文的实验。当改变多变量公钥密码中G的仿射函数时,会导致公钥、私钥和签名长度存在相应变化,相关参数值越大,对应安全级别越高[15]。该测试实验选取了随机64 位私钥密码分别经多变量公钥密码加密与SM2 椭圆曲线数字加密进行结果对比。从密文角度对图6 和图7 分析可得出,多变量公钥加密算法极大增强了私钥的保密性,也从中验证了提出的基于多变量公钥密码构建钱包安全保护模型的可实现性,但在区块链中更加关注签名的效率。文中对应用两种加密方式在安全级别为64 bit下进行对比分析,比较两者的签名验证时间,其结果如图8 所示。

图8 多变量公钥密码与SM2椭圆曲线数字加密耗时对比
从图8 可以看出,多变量公钥密码加密在签名与验证时间相较SM2 椭圆曲线数字加密会长很多,两项算法签名验证速度仅供参考。
3 结论
针对热钱包服务器存储私钥易遭受恶意入侵等问题,以及为优化抗量子加密算法,文中提出了一种基于多变量公钥密码构建热钱包安全保护方案,并对其中所提到的多变量公钥加密算法进行阐述、实现,得出以下结论:
1)提出文中方案的目的在于提升用户交易的安全性,所依据的理论框架重点在于对随机生成的私钥进行多变量公钥加密后生成密文1 保存在热钱包中,对密文1 使用SM2 椭圆曲线数字签名生成公钥。
2)提出多变量公钥密码加密算法体系的目的在于提升整体方案的安全性,验证方案的可实现性。文中利用具体实验操作,将多变量公钥密码加密密文与SM2 椭圆曲线数字加密密文对比,发现密文长度加长47%,签名耗时加长。当改变多变量公钥密码中G的仿射函数时,会导致公钥、私钥和签名长度存在相应变化,相关参数值越大,对应安全级别将更高。
3)多变量公钥加密算法实验的成功实现也意味着文中方案关键基础架构可实现。文中结合区块链交易中的技术特点,将多变量公钥密码算法应用于区块链热钱包底层技术中,为区块链上的交易数据提供安全性保护,可以有效应对区块链抗量子计算机攻击,也为未来区块链抵抗量子计算提供方向。
4)区块链+金融大多应用于智能软件,并且不会进行开源,因此,需要对Dapp 进行智能合约代码审计,或对该类Dapp 进行黑盒测试,从中寻出漏洞并进行妥善处理。
5)在金融智慧+智能合约方面,推广智能化区块链技术,并应用智能合约搭建起智慧化金融应用场景,以服务更多用户。
6)在区块链金融交易中,用户常以匿名方式或在境外进行交易。由于其匿名的影响,一旦发生攻击事件,若多国政策不互通,沟通不及时,处理不得当,则往往会产生重大影响,因此要加强区块链金融监管与立法保障交易安全。

