含LLC滤波的直流微电网非线性系统控制与仿真
高卫宏,侯 强
(山西晋中理工学院,山西 晋中 030600)
0 引言
直流母线电压控制是直流或混合交流/直流微电网系统运行中的一项重要任务。直流微电网中扰动以纹波为主,纹波是一种杂波信号,在直流母线上随机上下波动并随时间的变化呈现不同的周期性。在现有的研究中,文献[1]对直流母线电压扰动的不同类型进行了对比,总结了现有的维持直流母线电压稳定的方法,并对波动抑制方法的前景进行了展望;文献[2]分析了给系统造成谐波污染的设备,提出了一种频率分辨率高、计算量小的谐波、间谐波分析模型;文献[3]提出了一种基于非参数估计的电能质量监测设备运行可靠性分析方法,实现了对电能质量监测设备的可靠性远程分析与评估,有利于发现降低可靠性的隐患,提高电网公司的管理水平。基于这些文献并未提出如何减少直流母线纹波/谐波含量的问题,本文提出一种新型滤波方法,即将传统电压电流双闭环控制改为双闭环前馈控制[4],实时监测直流母线电压,滤除直流电网纹波,并加入LLC滤波,将直流母线扰动控制在一定区间内,得到更平滑的直流母线电压波形,保证直流电网电能质量。
1 直流微电网系统模型
本文所研究的系统主要为低频纹波。随着直流微电网不断扩大,主从控制下的直流微电网无法满足系统稳定性的要求,采用对等控制和下垂控制更满足现阶段复杂直流微电网控制的稳定性要求。光伏系统和复合储能系统通过电力电子变换器与直流母线电压相连接,进行能量传输和为负荷供电[5-6]。直流电网复合储能等效模型如图1所示。

图1 直流电网复合储能等效模型图

图2 双向DC/DC升降压电路图
光伏组在直流母线上传播能量的数学模型为
其中,IPH为光伏组往直流母线输送电流值;Iph为光伏输出电流;ID为二极管电流[7-8]。
复合储能在直流母线上传播能量的数学模型为
其中,IHESS为复合储能电流;Ibat为蓄电池组电流;Isc为超级电容器组电流;C为电容值。
2 双闭前馈环控制下的LLC滤波
2.1 双向DC/DC控制系统
双向DC/DC变换器控制模型如图3所示,数学模型如式(3)所示。

图3 双向DC/DC控制系统等效模型图[9]
开关导通时,DC/DC输入电压加到LLC滤波器的输入端,电感上的电流以固定斜率线性上升。开关关断时,由于电感上的电流不能突变,电感中存储的能量向负载释放,电感电流通过二极管续流,在这个阶段,电流波形是一条斜率为负的斜线。
电感值L的选取如式(4)所示。
2.2 双闭环前馈控制下直流微电网
直流微电网系统采用线性电压电流双闭环PI控制,并加入前馈电流环 Gf内环控制。控制情况如图4所示。其中双闭环中的电流环 Gi作为内环控制,和前馈电流环 Gf共同控制输入直流母线实际数值,双闭环中的电流环 Gi将电感电流和非线性干扰观测器输入到前馈电流环 Gf中的扰动电流放大k倍后进行对比,计算出误差值变为直流母线电压实际输出值Udc,再将直流母线电压实际输出值Udc与直流母线电压参考值Udc-ref进行对比,追踪直流母线电压扰动误差,通过LLC滤波器进行滤波。
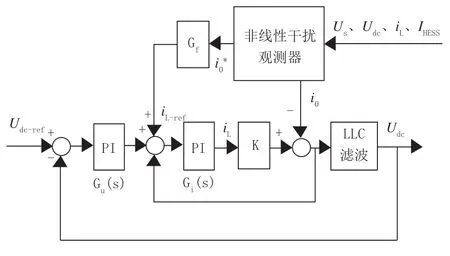
图4 DC/DC侧前馈控制系统等效模型图
2.3 LLC滤波器工作原理
交直流负载接入直流微电网时,所给电力系统带来的谐波污染利用原有双闭环控制系统无法稳定直流母线电压,保证电能质量。此时系统的谐波含量影响直流母线输出电压波形,综合考虑,本文将LLC滤波器接入电力系统,应用于直流电网DC/DC侧。LLC滤波器是一种谐振变换器,非常容易实现原边开关的零电压开关ZVS(zero voltage switch)[10]。LLC变换器是这样一种变换器,在输入高限下,前置功率因数校正器PFC(power factor correction)的正常输出电压,也即DC/DC的长期输入电压的开关损耗比其他已有的任何变换器都要小,所以其正常输入下的效率,不会因为要满足掉电保持时间而降低,仍然很高。利用变压器磁化电感电容滤波器可以实现零电压,降低整流器的电压应力。由于关断电流小,所以开关损耗小。变开关频率控制,不敏感的负载变化、频率变化可以设计的比采样率转换器SRC(sample rate convertor)更窄。操作范围宽,不降低正常操作效率。正是因为学术界对LLC变换器的上述优点进行了充分的宣传,使得这个拓扑不仅仅在服务器电源中受到了重视,还被用到了许多其他的领域,如通信设备中的开关电源、LED内的驱动电源、各种工业应用的电源和电动汽车的充电桩电源等。LLC滤波等效电路如图5所示。
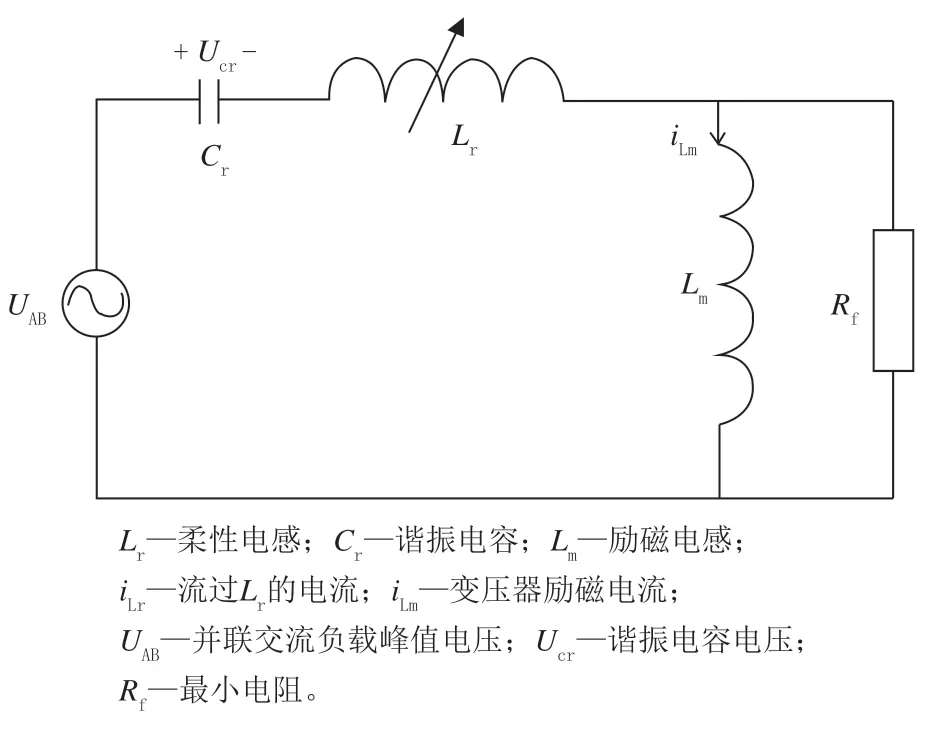
图5 LLC滤波等效电路模型图
电感比例系数h=Lm/Lr,LLC滤波电路有2个谐振频率fr和fm,如式(5)和式(6)所示。
LLC滤波电路全反馈如式(7)所示。
基于频域的直流增益:为了验证方便,将交流负载设置为阻性负载,交流激励源为单相电源,UAB设定为28 V不变,此时实际直流母线输入电压Udc与直流母线电压参考值Udc-ref相等为750 V,输出功率为780 W。式(8)和式(9)为LLC滤波电路传递函数和品质因素计算。
其中,H(jω)为传递函数;Q为品质因素;ωr是谐振频率fr的角速度;M为输入电压和输出电压比值。
由式(8)确定h值和Q值的直流增益,令Q=1/3,h取1~10。h=8,Q取0.1、0.2、0.3、0.4、0.5和0.6。其中,h值增加越高,幅值越小,电压越低,导致频率调节范围(输入或输出)变窄;h值选择越小时,直流增益大,但是根据式(h=Lm/Lr)表明,Lm减小,导致变压器励磁电流变大,在整个LLC滤波系统产生循环电流。同时,h值选择越小,也会引起系统稳定性问题。综上,h值选择不宜过小或者过大,应取3~8之间。
Q值越高,导致负荷调节越差,调节范围越窄,存在极值点,Q值的增加,极值点向右偏移,与f=1重合;Q值的减少,增益不能无限增加。在极值点时L也参与了谐振,对应的频率为f=1。在极值点的左侧,变换器工作在容性区域,可以实现零电流开关ZCS,电路损耗较大,一般避免工作在此区域。在极值点的右侧,变换器工作在感性区域,可以实现ZVS,正常设计变换器工作在此区域。在f=1时,表示只有谐振电容C和谐振电感L参与谐振,且开关频率等于谐振频率,此时电压增益始终为1,与0值的大小无关。因此,改变谐振变换器的开关频率能达到调节输出电压的作用。
3 参数设计
本文系统采用光伏直流输入,通过DC/DC变换器和全桥LLC滤波变换器相连接,通过直流母线将能量输出,其中双向DC/DC变换器采用非线性双闭环前馈控制,全桥LLC滤波变换器采用开环定频控制,两者通过控制系统将波形输入非线性干扰观测器,此时时间会有一个延迟,将非线性干扰观测器输出扰动值和谐波含量与参考值进行对比,通过开关频率的计算和直流输入采样值利用非线性干扰观测器控制系统,从而进一步对滤波系统进行控制。系统参数如表1所示。
4 仿真结果
本文为了验证理论,将滤波系统进行不同的分类,对比波形畸变率和扰动范围,具体情况如图6—图11所示。
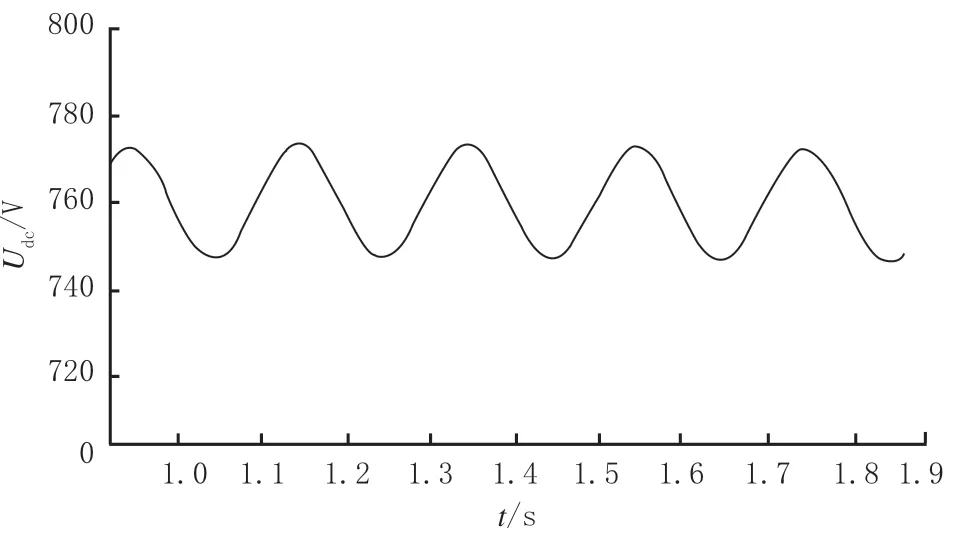
图6 输入电压450 V时仅有LLC滤波器的Udc仿真波形
由图6、图8和图10可知,输入电压450 V时仅有LLC滤波器的Udc仿真波形扰动范围为2.55 ~5.76 ,输入电压450 V时传统双闭环控制+LLC滤波器的Udc仿真波形扰动范围为1.10 ~3.80 ,输入电压450 V时非线性干扰观测器前馈控制+LLC滤波器的Udc仿真波形扰动范围为0.04 ~1.28 ,扰动减少2.51 ~4.48 ;由图7、图9和图11可知,输入电压450 V时仅有LLC滤波器的Udc谐波畸变率为1.8 ,输入电压450 V时传统双闭环控制+LLC滤波器的Udc谐波畸变率为0.91 ,输入电压450 V时非线性干扰观测器前馈控制+LLC滤波器的Udc谐波畸变率为0.42 ,降低了1.38 。

图7 输入电压450 V时仅有LLC滤波器的Udc谐波畸变率
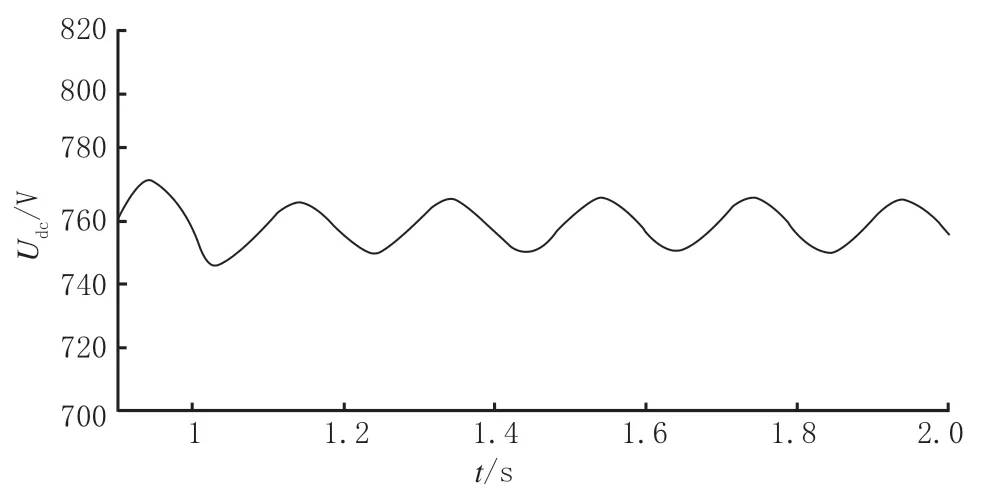
图8 输入电压450 V时传统双闭环控制+LLC滤波器的Udc仿真波形
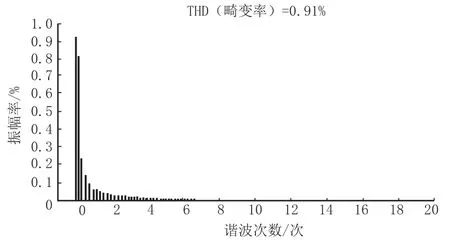
图9 输入电压450 V时传统双闭环控制+LLC滤波器的Udc谐波畸变率

图10 输入电压450 V时非线性干扰观测器前馈控制+LLC滤波器的Udc仿真波形
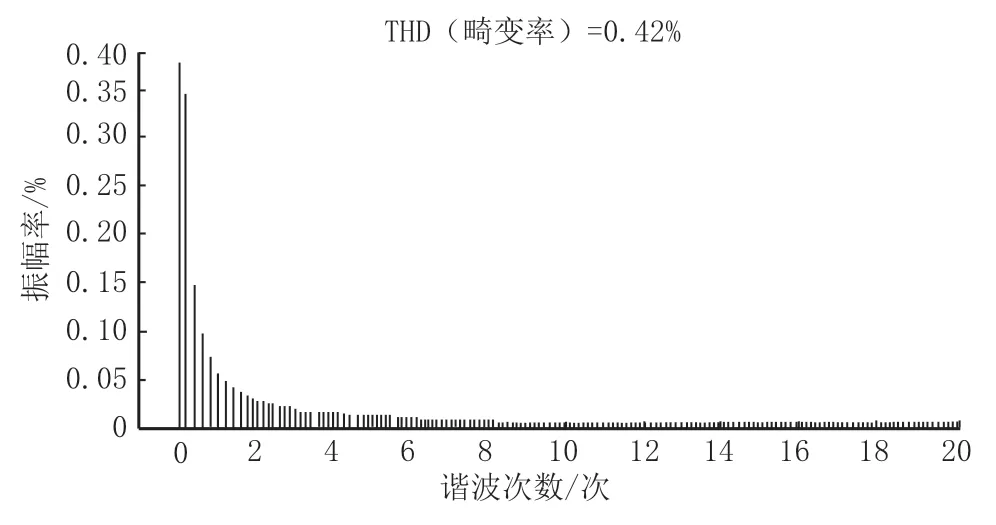
图11 输入电压450 V时非线性干扰观测器前馈控制+LLC滤波器的Udc谐波畸变率
5 结论
本文研究了含LLC滤波的直流微电网非线性系统控制与仿真,将分布式电源通过DC/DC变换器与直流母线连接,采用双闭环前馈控制+DC/AC交流侧LLC滤波系统,通过非线性干扰观测器追踪系统扰动,同时进行谐波分析,对比系统谐波畸变率和波动范围,保证电能质量,提高系统经济性。分析后结论如下:
a)本文所提滤波方法维持了直流电网电压稳定,优化了控制策略。扰动范围从2.55 ~5.76 降低到0.04 ~1.28 ,降低了2.51 ~4.48 ;谐波畸变率由1.80 降低到0.42 ,降低了1.38 。证明本文提出的控制策略是有效的。
b)直流电压采用非线性前馈控制,LLC滤波采用定频控制,能够在宽电压范围内维持电压等级高的线路恒定,减小输入直流母线上的电流纹波,缩小滤波器尺寸,消弱电磁干扰,降低输出电容纹波电流,从而增加变换器的使用年限,可应用于电压等级高、传输功率大的电力线路。

