一种改进WVSSA算法的GNSS时间序列降噪方法

侯增楠，黄征凯，王 琰，孙喜文，贺小星，黄佳慧，乔丽娜

一种改进WVSSA算法的GNSS时间序列降噪方法

侯增楠1，黄征凯1，王 琰2，孙喜文3，贺小星4，黄佳慧4，乔丽娜1

（1. 华东交通大学 交通运输工程学院，南昌 330013；2. 河北供水有限责任公司，石家庄 050000；3. 东华理工大学 测绘工程学院，南昌 330032；4. 江西理工大学 土木与测绘工程学院，江西 赣州 341000）

针对变分模态分解（VMD）中不适合的模态分解数和惩罚因子易出现过度分解与分解不足等现象的问题，提出一种改进VMD和利用复合指标改进奇异谱分析（SSA）的鲸鱼变分模态奇异谱分析（WVSSA）方法：采用WOA算法确定VMD分解的最佳参数组合进行VMD分解和重构；并用基于复合评价指标改进的SSA方法进行二次降噪；最后利用10个基准站与仿真信号分解降噪以验证方法的有效性。周期信号与噪声信号降噪分析结果表明，WVSSA方法与经验模态分解（EMD）、集合经验模态分解(EEMD）相比，均方根误差降低0.6222、0.6053 mm，信噪比增加1.0349、1.0298 dB，相关性增加0.0645、0.0625；全球卫星导航系统（GNSS）时序降噪分析结果表明，WVSSA方法均方根误差比EMD、EEMD平均降低0.9156、0.8271 mm，信噪比平均增加2.7606、2.4727 dB，相关性平均增加0.1754、0.1531。WVSSA方法在时间序列识别和去除噪声上更为有效。

鲸鱼优化算法（WOA）；变分模态分解（VMD）；奇异谱分析（SSA）；复合评价指标；经验模态分解（EMD）；集合经验模态分解(EEMD）

0 引言

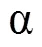
1 WVSSA原理

1.1 VMD原理

VMD分解通过迭代方式来求解最优中心频率和带宽，对信号构造并求解约束变分问题[11]。约束问题模型为

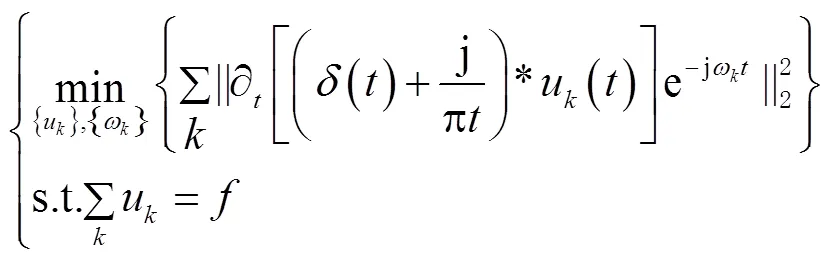
1.2 WOA优化VMD参数

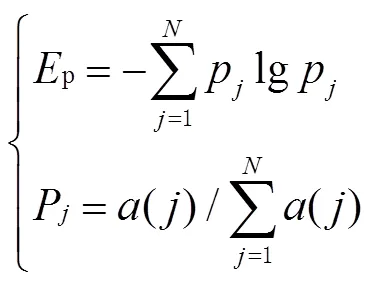
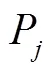
式中：*为卷积运算符；()为VMD分解的个模态分量。

1.3 SSA原理

SSA是一种研究非线性时间序列的方法，它首先选取在区间（1，N/2）内的窗口长度、时间序列的长度，构造一个•的轨迹矩阵，构建形式如式（5）、式（6）所示。

原始序列为

轨迹矩阵为

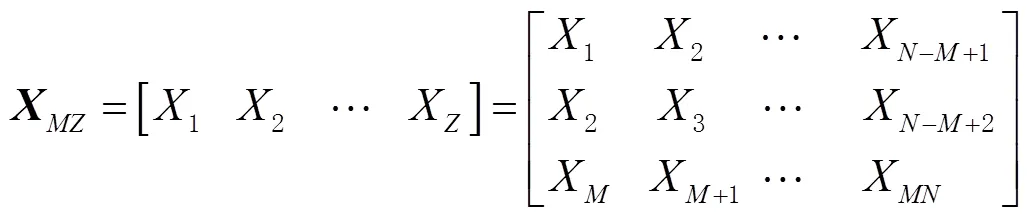
其中为

随后通过求解轨迹矩阵的特征值和特征向量，将对角阵从大到小进行排列、分解，确定时间序列成分进行重构，重构公式如式（8）所示，重构后进行分组重组。

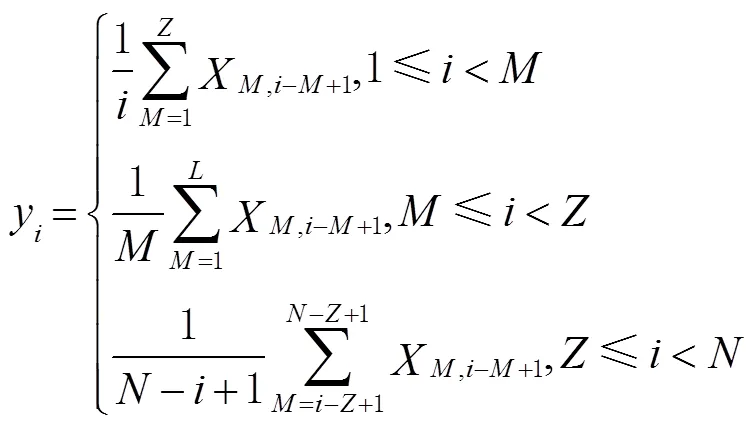
1.4 WVSSA算法流程

由WOA、VMD、SSA组合后的WVSSA去噪算法流程如下：

2）通过连续求和VMD分解的每个模态分量来重构时间序列，并计算每个重构时间序列的综合评价指数值。当值最小时，相应的重构时间序列是去噪时间序列，剩余的IMF分量被视为高频噪声。

3）剩余噪声序列经过奇异谱分析进一步降噪，此时选用时间序列长度一半作为窗口长度来构造轨迹矩阵，进行奇异值分解，对重组后的序列采用复合评价指标来进行去噪序列提取重构，得到的去噪序列与步骤2）中的去噪序列重构。

2 GNSS时间序列降噪分析

本文基于WOA、VMD和SSA原理，提出一种基于WOA确定VMD最佳参数组合与奇异谱分析降噪相融合的WVSSA方法。

2.1 周期信号与噪声信号降噪分析

因实测数据真值未知，故采用真值已知的仿真时间序列验证本文方法。本文选用白噪声+幂律噪声（white noise，power law，WN+PL）组合模型的一组周期仿真信号进行降噪分析，周期信号选用 3个恒定的振幅周期信号和噪声模型组成，采样频率为3652个，采样频率为1 Hz，噪声选用4 dB高斯白噪声、幅度0.04 mm幂律噪声[15]。3个恒定振幅周期信号及噪声信号如图1所示。

图1 恒定振幅周期信号

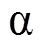
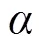
由图3可知，VMD分解过程中没有出现模态混叠问题。为了提取到有用信号，将IMF分量依次（分别在图中表示为mf1～mf6）进行累加重构，计算其复合评价指标（如表1所示）。

图2 最优解收敛变换

图3 VMD模态分量及对应频谱

表1 复合评价指标

由表1可知，在=2时的重构序列复合评价指标值值最小，此时的序列为去噪序列，mf3～mf6序列中含有高频噪声，剩余高频噪声进行SSA二次降噪。同时进行EMD和EEMD降噪处理，并与本文方法对比，降噪对比结果如图4所示。对其降噪结果进行精度评价，其精度评价结果如表2所示。

表2 精度评价结果

图4 降噪结果

由图4可看出，WVSSA方法相比于EMD和EEMD方法，降噪后的数据更接近真实值。由表2可知，周期信号加入WN+PL噪声后的数据经过EMD、EEMD和本文方法降噪后，进行均方根误差、信噪比、相关性结果的对比，WVSSA方法总体上优于EMD和EEMD方法，其均方根误差比EMD、EEMD分别降低0.6222、0.6053 mm，信噪比分别增加1.0349、1.0298 dB，相关性分别增加0.0645、0.0625。因均方根误差更小，表明其具有更小的偏差；信噪比值越大，其有用信号越多；相关系数指标上更大，表明其与原始数据拟合度高：由此可得，WVSSA方法降噪效果优于EMD和EEMD方法。

2.2 GNSS时序降噪分析

为了进一步验证此方法的有效性和可靠性，选用10个GNSS基准站，时间跨度为11～12 a的时间序列，采样间隔为1/365.25 a，采用EMD、EEMD和本文方法对站点时间序列进行降噪处理。图5为站点序号7ODM站点时间跨度为2010—2021年的N、E、U 3个方向的时间序列降噪对比结果。

由图5可知，WVSSA方法相比EMD和EEMD具有更好的降噪效果。通过对其余9个站点降噪处理后，对降噪后数据进行精度评定，结果如表3所示。

表3 精度评价结果

图5 降噪对比结果

由表3可知， WVSSA方法均方根误差比EMD、EEMD分别平均降低了0.9156、0.8271 mm，信噪比分别平均增加2.7606、2.4727 dB，相关性分别平均增加0.1754、0.1531。均方根误差越小，相关性越大、信噪比越大，所得的结果越好。综上所述，文本提出的WVSSA方法比EMD和EEMD降噪效果好，可靠性高。

3 结束语

本文针对变分模态分解中不适合的模态分解数和惩罚因子出现过度分解与分解不足等现象提出一种改进变分模态分解和利用复合指标改进的奇异谱分析的WVSSA方法，采用仿真信号和GNSS站点数据验证该方法的有效性和可靠性，得出以下结论：

1）WVSSA方法相较于EMD、EEMD方法，具有更高的相关性、更低的均方根误差以及更高的信噪比，表明WVSSA方法具有更好的降噪效果。

2）利用复合评价指标改进的奇异谱分析法，能够更有效地解决奇异谱分析法中去噪信号提取的问题，提高GNSS序列降噪的效率。

目前，本文的研究仅使用部分区域站点的GNSS时间序列进行可靠性分析。下一步的研究将扩展到不同地区和不同时间跨度的GNSS时间序列数据，通过使用更多的站点数据和更广泛的时间范围，进一步验证WVSSA方法的有效性。

[1] 姜卫平, 李昭, 刘万科, 等. 顾及非线性变化的地球参考框架建立与维持的思考[J]. 武汉大学学报(信息科学版), 2010, 35(6): 665-669.

[2] 王敏, 沈正康, 董大南. 非构造形变对GPS连续站坐标时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052.

[3] 姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报(信息科学版), 2018, 43(12): 2112-2123.

[4] 李昭, 姜卫平, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列噪声模型建立与分析[J]. 测绘学报, 2012, 41(4): 496-503.

[5] 贺小星. GPS 坐标序列噪声模型估计方法研究[J]. 测绘学报, 2017, 46(3): 398.

[6] 张恒璟, 程鹏飞. 基于EEMD的GPS高程时间序列噪声识别与提取[J]. 大地测量与地球动力学, 2014, 34(2): 79-83.

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]// Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[8] 钱文龙, 鲁铁定, 贺小星, 等. GPS高程时间序列降噪分析的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(3): 242-246, 269.

[9] 鲁铁定, 钱文龙, 贺小星, 等. 一种确定分界IMF分量的改进EMD方法[J]. 大地测量与地球动力学, 2020, 40(7): 720-725.

[10] 鲁铁定, 钱文龙, 贺小星, 等. 一种削弱信噪混叠的EMD降噪方法[J]. 大地测量与地球动力学, 2020, 40(2): 111-116.

[11] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[12] RobertVautard, PascalYiou, Michael. Ghil singular-spectrum analysis: A toolkit for short, noisy chaotic signals[J]. Physcia D, 1992, 158(1/2/3/4): 95-126.

[13] Seyedail M,Andrew L. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.

[14] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81.

[15] 孙喜文, 贺小星, 黄佳慧, 等. 一种CEEMDAN的坐标时间序列降噪新方法[J/OL]. 导航定位学报, [2022-5-13]. https://kns.cnki.net/kcms/detail/10.1096.P.20220512.1821.008.html.

A noise reduction method for GNSS time series based on improved WVSSA algorithm

HOU Zengnan1,HUANG Zhengkai1, WANG Yan2, SUN Xiwen3, HE Xiaoxing4, HUANG Jiahui4, QIAO Lina1

（1. School of Transportation Engineering, East China Jiaotong University, Nanchang 330013, China;2. Hebei Water Supply Co., Ltd., Shijiazhuang 050000, China;3. School of Surveying and Mapping Engineering, Donghua University of Technology, Nanchang 330032, China;4. School of Civil Engineering and Surveying and Mapping Engineering, Jiangxi University of Technology, Ganzhou, Jiangxi 341000, China）

Aiming at the problem that it is liable to excessive decomposition and insufficient decomposition for unsuitable modal decomposition numbers and penalty factors in variational mode decomposition (VMD), the paper proposed a method of whale optimization algorithm variable modal decomposition singular spectrum analysis (WVSSA) to improve VMD and use composite index to improve singular spectrum analysis (SSA): WOA algorithm was used to determine the best parameter combination of VMD decomposition for VMD decomposition and reconstruction; and the improved SSA method based on composite evaluation index was used to carry out secondary noise reduction; finally, 10 reference stations and simulated signals were used to decompose and reduce noise to verify the effectiveness of the method.Results of periodic signal and noise signal denoising analysis showed that compared with empirical mode decomposition (EMD) and ensemble empirical mode decomposition (EEMD), the root-mean-square error of WVSSA method would be reduced by 0.6222 and 0.6053 mm, the signal-to-noise ratio (SNR) would be increased by 1.0349 and 1.0298 dB, and the correlation would be increased by 0.0645 and 0.0625; meanwhile, results of global navigation satellite system (GNSS) sequential noise reduction analysis showed that the root-mean-square error of WVSSA method would be lower than that of EMD and EEMD by 0.9156 and 0.8271 mm on average, the SNR would be increased by 2.7606 and 2.4727 dB on average, and the correlation would be increased by 0.1754 and 0.1531 on average. In general, WVSSA method could be more effective in time series identification and noise removal.

whale optimization algorithm (WOA); variational mode decomposition (VMD); singular spectrum analysis (SSA); composite evaluation index; empirical mode decomposition (EMD); ensemble empirical mode decomposition (EEMD)

侯增楠, 黄征凯, 王琰, 等. 一种改进WVSSA算法的GNSS时间序列降噪方法[J]. 导航定位学报, 2023, 11(4): 97-103.（HOU Zengnan, HUANG Zhengkai, WANG Yan, et al. A noise reduction method for GNSS time series based on improved WVSSA algorithm[J]. Journal of Navigation and Positioning, 2023, 11(4): 97-103.）DOI:10.16547/j.cnki.10-1096.20230414.

P228

A

2095-4999(2023)04-0097-07

2022-11-08

国家自然科学基金项目（41904002，42104023）；江西理工大学高层次人才科研启动项目（205200100588，205200100）；江苏省自然科学基金项目（BK 20190691）。

侯增楠（1998—），男，山西吕梁人，硕士研究生，研究方向为GNSS数据处理。

黄征凯（1988—），男，江西赣州人，博士，讲师，研究方向为卫星测高数据处理及应用。