川渝地区大气加权平均温度模型优化

侯晓玲，熊永良

川渝地区大气加权平均温度模型优化

侯晓玲，熊永良

（西南交通大学 地球科学与环境工程学院，成都 611700）

为了弥补川渝地区还没有本地化加权平均温度（m）模型的不足，提出一种川渝地区大气加权平均温度模型优化方法：选取甘孜、温江、西昌、沙坪坝4个站2017—2019年的探空数据，根据最小二乘法进行线性拟合，构建适用于川渝地区的加权平均温度模型。实验结果表明，本地化模型的平均绝对误差（MAE）和均方根误差（RMSE）均值分别为1.24和1.60 K，均优于贝维斯（Bevis）模型和中国加权平均温度回归模型；在本地化模型基础上加入季节性改正后的三角函数值、测站高程和大地纬度因素，新构建的本地化加权平均温度优化模型较本地化模型能取得更高的精度。提出的本地化加权平均温度模型在川渝地区可有较好的适用性，能够为全球导航卫星系统（GNSS）在当地气象行业的应用提供参考。

川渝地区；加权平均温度；最小二乘；线性拟合；优化模型

0 引言

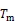
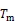
1 数据处理方法

1.1 加权平均温度计算

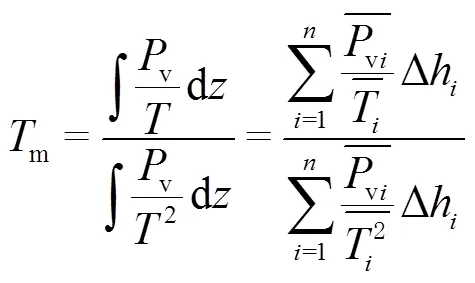
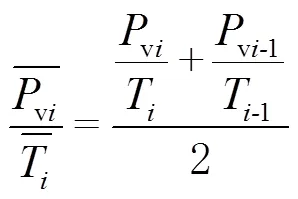
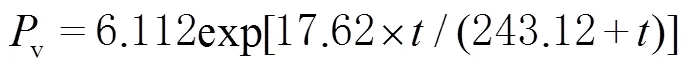
式中：exp()为以自然常数e为底的指数函数；为露点温度（单位为℃）。

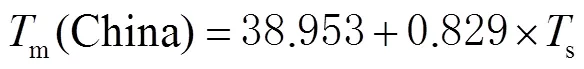
1.2 精度评估方法

本文采用平均绝对偏差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）2个度量标准进行模型精度的检验，即有：

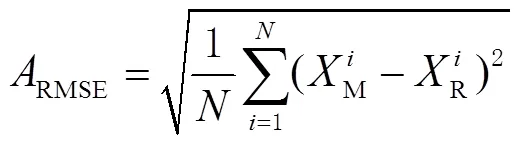
2 川渝地区模型的建立及精度分析

2.1 数据来源

从美国怀俄明大学天气数据网（http:// weather. uwyo.edu/upperair/sounding.html）下载川渝地区4个探空站（甘孜、温江、西昌、沙坪坝）2017—2019年每天协调世界时（universal time coordinated，UTC）0时和12时采集的实测数据，其中包括气压、高度、地面温度、露点温度、大气厚度、相对湿度、大气可降水量等参数，该机构对发布的探空数据按照世界气象组织（World Meteorological Organization，WMO）制定的规则均已进行了质量检查。如图1所示是川渝地区4个探空站的位置分布，如表1所示为对应的地理位置信息。

表1 川渝地区4个探空站位置信息

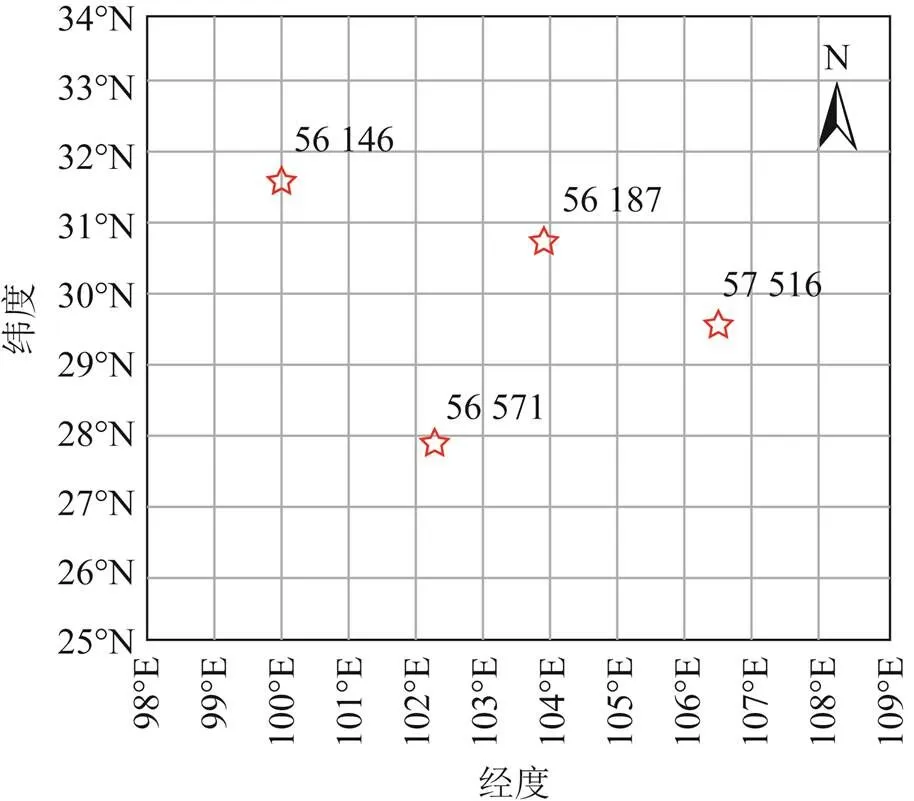
图1 川渝地区4个探空站分布

2.2 本地化模型

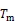
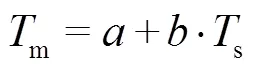
式中：a为常数项；b为回归系数。

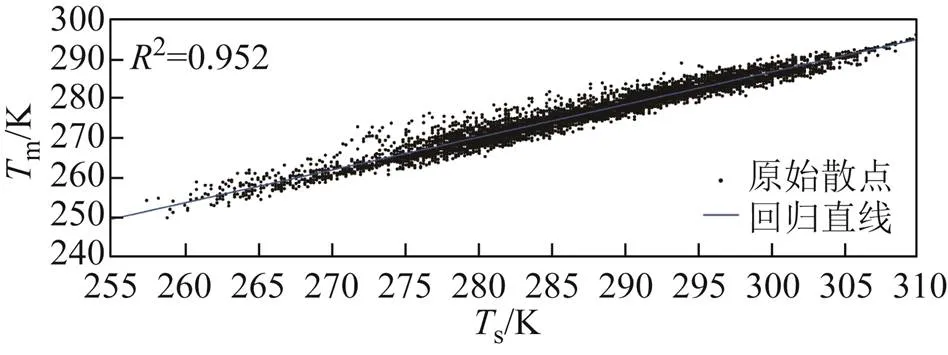
图3 与相关性分析

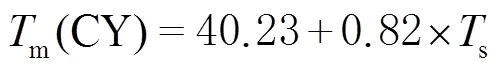
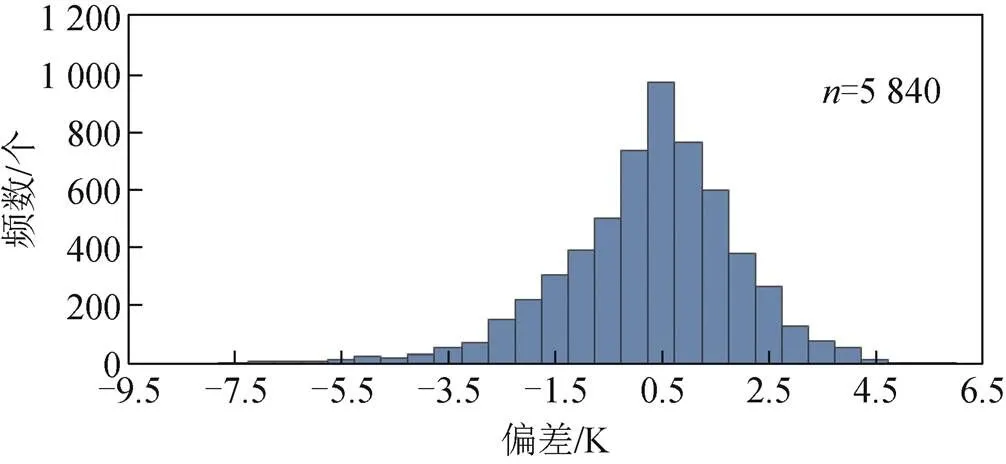
图4 模型残差分布直方图

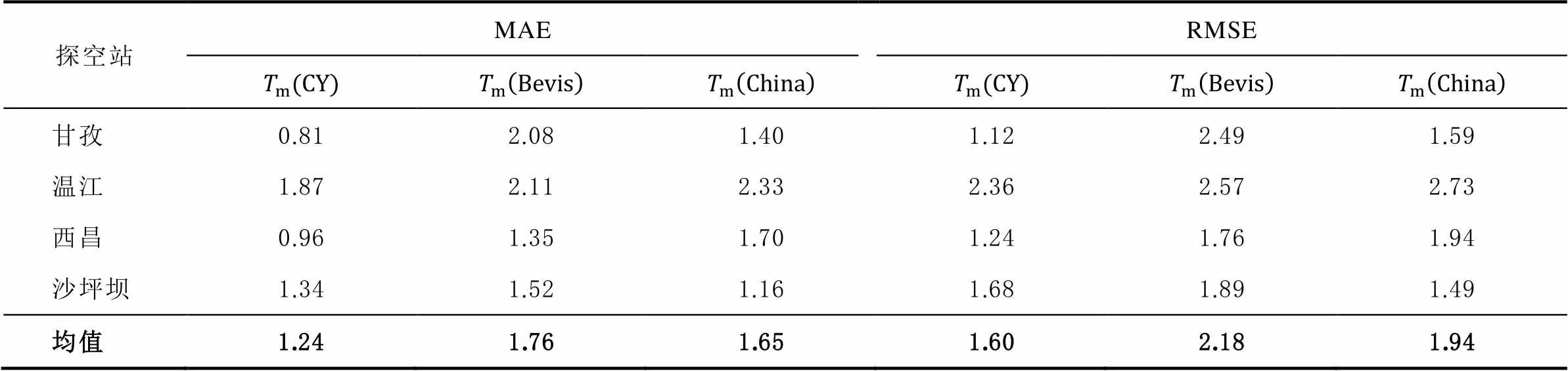
表2 Tm模型精度比较 K

图5 2017—2018年模型偏差分析

2.3 本地化模型的优化

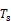
表3 优化模型的拟合系数

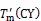
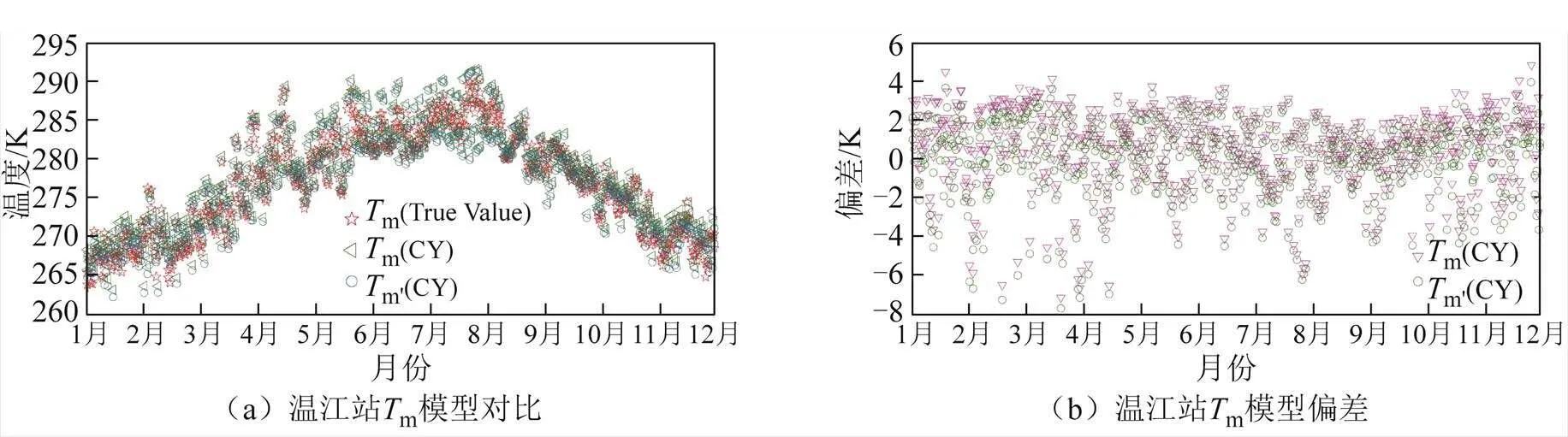
图6 2019年温江站模型分析

表4 温江站模型预测精度统计 K

3 结束语

[1] ROCKEN C, HOVE T V, WARE R. Near real-time GPS sensing of atmospheric water vapor[J]. Geophysical Research Letters, 2013, 24(24): 3221-3224.

[2] 青盛. 地基GPS水汽反演的研究[D]. 成都: 西南交通大学, 2009.

[3] 王晓英, 戴仔强, 曹云昌, 等. 中国地区地基GPS加权平均温度Tm统计分析[J]. 武汉大学学报(信息科学版), 2011, 36(4): 421-416.

[4] 姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227.

[5] 刘志赵, 刘经南, 李征航. GPS技术在气象学中的应用[J]. 测绘通报, 2000(2): 8-9.

[6] BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology:Remote sensing of atmospheric water vapor using the global positioning system[J]. Journal of Geophysical Research: Atmospheres, 1992, 97(D14): 15787-15801.

[7] 陈鹏, 陈家君. 利用NCEP再分析资料建立全球大气加权平均温度模型[J]. 大地测量与地球动力学, 2014, 34(3): 133-136.

[8] ROSS R J, ROSENFELD S. Estimating mean weighted temperature of the atmosphere for global positioning system applications[J]. Journal of Geophysical Research Atmospheres, 1997, 102(D18): 21719-21730.

[9] 王皓, 赵兴旺. 香港地区大气加权平均温度建模与研究[J]. 全球定位系统, 2019, 44(1): 119-124.

[10] 郭彬洋, 李黎, 谢威, 等. 长三角地区加权平均温度本地化模型拟合[J]. 导航定位学报, 2019, 7(2): 61-67.

[11] 杨林, 郑南山, 高淑照, 等. 基于BP神经网络算法构建香港地区加权平均温度模型[J]. 导航定位学报, 2021, 9(4): 92-97.

[12] 张洛恺, 杨力, 王艳玲, 等. 郑州地区大气加权平均温度模型确定[J]. 测绘科学技术学报, 2014, 31(6): 566-569.

[13] NME A, MAA A, AEM B, et al. GNSS meteorology in Egypt: Modeling weighted mean temperature from radiosonde data[J]. Alexandria Engineering Journal, 2019, 58(2): 443-450.

[14] LIU Y, CHEN Y. Determination of weighted mean tropospheric temperature using ground meteorological measurements[J]. Geo-Spatial Information Science, 2001, 4(1P): 14-18.

[15] 刘焱雄, 陈永奇, 刘经南. 利用地面气象观测资料确定对流层加权平均温度[J]. 武汉测绘科技大学学报, 2000(5): 400-404.

[16] 胡伍生, 王来顺, 朱明晨, 等. 中国区域加权平均温度的建模研究[J]. 现代测绘, 2018, 41(3): 21-23.

[17] YAO Y B, ZHANG B, XU C Q, et al. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based GPS meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282.

An optimization method of weighted mean temperature model in Sichuan-Chongqing region

HOU Xiaoling, XIONG Yongliang

（Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611700, China）

Sichuan-Chongqing region; weighted mean temperature; least square; linear fitting; optimized model

侯晓玲, 熊永良. 川渝地区大气加权平均温度模型优化[J]. 导航定位学报, 2023, 11(4): 63-69.（HOU Xiaoling, XIONG Yongliang. An optimization method of weighted mean temperature model in Sichuan-Chongqing region[J]. Journal of Navigation and Positioning, 2023, 11(4): 63-69.）DOI:10.16547/j.cnki.10-1096.20230409.

P228

A

2095-4999(2023)04-0063-07

2022-10-25

四川省科技计划资助项目（2022YFG0169）

侯晓玲（2000—），女，江苏南通人，硕士研究生，研究方向为GNSS气象学。

熊永良（1964—），男，四川泸州人，博士，教授，研究方向为GNSS理论与应用。