一类具有非线性项的弱耦合半线性双波动系统全局解的非存在性

欧阳柏平, 侯春娟

(广州华商学院数据科学学院, 广州 511300)

近几十年来,有关非线性项下弱耦合半线性波动方程和波动系统柯西问题解的全局存在性及爆破问题成为了学者们关注的热点。部分学者[1-7]研究了以下二阶半线性波动系统解的爆破问题:

其中,q、p>1,n≥1,ε>0,Δ是拉普拉斯算子。该二阶半线性波动系统的临界曲线为

当αW<(n-1)/2时,在初始数据满足一定的约束条件下存在全局解;当αW≥(n-1)/2时,其解爆破。

CHEN和REISSIG[8]考虑了如下具有阻尼项的弱耦合半线性波动系统解的爆破问题:

其中,q、p>1,ε>0。该文应用迭代技巧推出了初始数据满足一定条件时解的爆破及其生命跨度估计。

高阶半线性波动方程解的爆破已有很多研究成果[9-16],如:CHEN和PALMIERI[9]讨论了以下半线性Moore-Gibson-Thompson(MGT)方程解的柯西问题:

其中,ε>0,p>1,β、ε>0。该文应用迭代方法和切片方法,分别得到了在次临界、临界情况下解的全局非存在性和生命跨度估计。

双波动模型是基本波动方程的一个推广。特别地,如果将div算子作用于弹性波方程utt-a2Δu+(b2-a2)∇divu=0,则可得到一类双波动方程。

本文考虑如下具有非线性项的弱耦合半线性双波动系统柯西问题解的爆破现象:

(1)

本文采用迭代思路和切片方法对问题(1)进行探讨,避开了由于无界乘子的引入而使得Kato引理难以应用的问题。首先,构造若干能量泛函,得到其迭代框架和第一下界;然后,运用迭代技巧推导出问题(1)全局解的非存在性以及生命跨度估计。

1 预备知识

首先给出方程组(1)的柯西问题弱解的定义:

定义1设(u0,u1,u2,u3,v0,v1,v2,v3)(H3(n)×H2(n)×H1(n)×L2(n))×(H3(n)×H2(n)×H1(n)×L2(n))。称(u,v)为问题(1)在[0,T)上能量弱解,如果

uC([0,T),H3(n))∩C1([0,T),H2(n))∩

C2([0,T),H1(n))∩C3([0,T),L2(n))∩

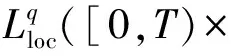
vC([0,T),H3(n))∩C1([0,T),H2(n))∩

C2([0,T),H1(n))∩C3([0,T),L2(n)∩

满足

(2)

和

(3)

其中,φ(t,x),ψ(t,x)[0,T)。

对式(3)和式(4)应用分部积分,可得

(4)

和

(5)

令t→T,则(u,v)满足方程组(1)给出的弱解的定义。

下面给出本文定理证明所需引理。

引理1[10]函数Φ(x)定义如下:

其中,xn,n-1为n-1维球面。Φ(x)为正光滑函数,且 ΔΦ(x)=Φ(x),Φ(x)～|x|-(n-1)/2e|x|(|x|→∞)。

引理2[11]函数Ψ的渐近性如下:

(6)

其中,c1>0,Ψ=Ψ(t,x)=e-tΦ(x),Φ(x)的定义见引理1,p′=p(p-1),BR+t表示以原点为中心、R+t为半径的球。

2 主要结论

本文的主要结果如下:

定理1设p,q>1且p,q<(n+4)/(n-4),如果n>4,则

设(u0,u1,u2,u3,v0,v1,v2,v3)(H3(n)×H2(n)×H1(n)×L2(n))2,其中ui,vi(i=0,1,2,3)是不恒为0的具有非负紧支集的函数,包含在半径为R的球BR中。特别地,假设u3(x)+u2(x)>u1(x)+u0(x),v3(x)+v2(x)>v1(x)+v0(x),如果(u,v)是方程组(1)的解,其生命跨度T(ε)满足

suppu(t,·),suppv(t,·)⊂Bt+R(t(0,T)),

则存在一个正常数ε0,使得当ε(0,ε0]时,(u,v)在有限时间爆破, 其生命跨度的上界估计为

证明定义如下泛函

(7)

由波动方程有限传播速度和定理条件,可知当(u0,u1,u2,u3,v0,v1,v2,v3)(H3(n)×H2(n)×H1(n)×L2(n))2在BR中具有紧支集时,问题(1)的局部弱解属于其能量空间并且在BR+t中具有紧支集。

在式(4)、(5)中,选取φ≡1和ψ≡1,{(s,x)[0,t]×n:|x|≤R+s},有

(8)

(9)

结合式(7)～(9),得到

(10)

(11)

对式(10)关于t积分3次,可得

(12)

由Hölder不等式及suppv(t,·)⊂Bt+R(t(0,T)),可推出

(13)

其中C1>0。

将式(13)代入式(12),可得

(14)

同样,对式(11)在[0,t]上积分3次,整理得到

(15)

其中C2>0。

式(14)、(15)提供了迭代框架。下面推导U和V的下界序列及其第一下界。由引理2,有

定义泛函U0(t)、V0(t)为:

(16)

式(3)中令Ψ=φ,易得

(17)

其中,Ψ(t,x)[0,T)。

对于式(17),进一步由分部积分和Ψ的性质,得到

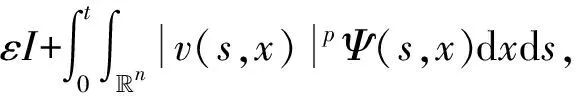
(18)

其中

I=I[u0,u1,u2,u3]=

结合式(16)和式(18),有

G′(t)+2G(t)≥εI。

(19)

对式(19)积分,有

(20)

从而可得

(21)

对式(21)关于t积分2次,得到

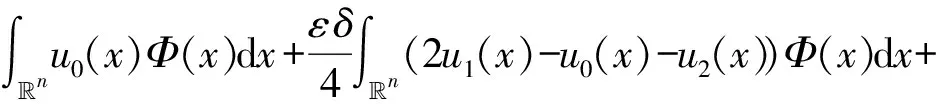
(22)

其中C0>0。

类似地,可得

(23)

由Hölder不等式、式(6)和式(23),有

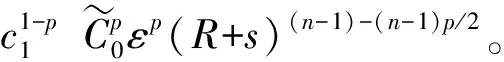
(24)

联立式(14)和式(24),可得

U(t)≥

(25)

类似地,由式(15)和式(22),有

V(t)≥

(26)

U(t)≥D1(R+t)-α1tβ1,

(27)

V(t)≥Q1(R+t)-a1tb1。

(28)

下面构造U(t)和V(t)的迭代序列。具体地说,设

U(t)≥Dj(R+t)-αjtβj,

(29)

V(t)≥Qj(R+t)-ajtbj,

(30)

其中,{Dj}j、{Qj}j、{αj}j、{aj}j、{βj}j、{bj}j均为非负实序列。

由式(27)和式(28)可知,j=1时,式(29)和式(30)成立。假设j>1时,式(29)、(30)成立,下证式(29)、(30)对j+1也成立。

由式(14)、(15)、(29)、(30),可得

(31)

(32)

设

(34)

于是,由式(31)～(34)可知式(29)和式(30)对j+1成立。

下面对αj、βj、aj、bj进行估计。设j为奇正整数,由式(33)、(34)可得

αj=n(p-1)+p(n(q-1)+qαj-2)=… =

aj=n(q-1)+qn(p-1)+pqaj-2=…=

(35)

同样可得

(36)

当j为偶正整数时,j-1为正奇数,故有

(37)

由式(36)、(37),可知

(1)当j为奇正整数时,

(2)当j为偶正整数时,

下面估计Dj和Qj。结合式(33)～(37),有

由此可得

(38)

(39)

当j为奇正整数时,对式(38)两边取对数,由递推关系,得到

logDj≥logE0+pqlogDj-2-(2p(j-1)+2j)log(pq)≥

[2pq+(pq-1)j]。

(40)

设j0为满足下式的最小正整数:

则式(40)可化为

logDj≥

(pq)(j-1)/2log(E1εp),

(41)

其中,E1=E1(n,p,q),j≥j0。

由式(39),类似可得

logQj≥

(42)

当j为奇正整数且j≥max{j0,j1}时,由式(29)、(35)、(36)、(41),有

U(t)≥exp((pq)(j-1)/2log(E1εp))×

(R+t)n-(n+(n-1)p/2)(pq)(j-1)/2t((4+4p)/(pq-1)+n+3)(pq)(j-1)/2-(4+4p)/(pq-1)=

当t≥R时,有

U(T)≥exp((pq)(j-1)/2(log(E1εp2-(n+(n-1)p/2)×

t(4+4p)/(pq-1)+n+3-(n+(n-1)p/2))))(R+t)nt-(4+4p)/(pq-1)。

(43)

式(43)右边项指数函数中t的指数为

pΥ1(n,p,q)。

当Υ1(n,p,q)>0时,t的指数是正的。

类似的推导,联立式(30)、(35)、(36)、(42),得到

t(4+4q)/(pq-1)+n+3-(n+(n-1)q/2))))(R+t)nt-(4+4q)/(pq-1),

(44)

其中t≥R。

此时,式(44)右边项指数函数中t的指数为

qΥ2(n,p,q)。

当Υ2(n,p,q)>0时,t的指数是正的。

设ε0=ε0(u0,u1,u2,u3,v0,v1,v2,v3,n,p,q,R)>0,使得

记E2=(E12-(n+(n-1)p/2))-1/(pΥ1(n,p,q))。当ε(0,ε0]和t>E2ε-1/Υ1(n,p,q)时,有t≥R和log(E1εp×2-(n+(n-1)p/2)tpΥ1(n,p,q))>0。

式(43)中,对j→∞,当ε(0,ε0]和t>E2ε-1/Υ1(n,p,q)时,可得U(t)的下界爆破。

同理,当Υ2(n,p,q)>0时,对于合适的ε0=ε0(u0,u1,u2,u3,v0,v1,v2,v3,n,p,q,R)>0,有

因而,当ε且时,令j→∞,可推出V(t)的下界爆破。

由以上讨论可知,问题(1)的全局解不存在,进一步可得局部解(u,v)的生命跨度估计为