基于留一交叉验证法的APSIM-Maize产量模拟

杨雪宁 张永强 张选泽 马 宁 张俊梅

研究简报

基于留一交叉验证法的APSIM-Maize产量模拟

杨雪宁1,2张永强1,*张选泽1马 宁1张俊梅3

1中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室, 北京 100101;2中国科学院大学中丹学院, 北京 100101;3达拉特旗农业技术推广中心, 内蒙古达拉特 014300

作物生长模型APSIM广泛应用于作物估产和农业生产管理中, 在观测数据有限的情况下, 开展留一交叉验证是提高模型模拟能力的关键途径。本研究以内蒙古十大孔兑地区春玉米为研究对象, 量化分析了APSIM-Maize模型模拟2012—2019年间玉米产量对关键参数的敏感性, 并根据参数敏感性强弱对APSIM-Maize模型进行交叉验证与参数率定, 提高了模型模拟能力。主要结果为: (1) 影响春玉米产量的敏感性参数由强到弱依次是: 蒸腾效率系数、辐射利用效率、开花到成熟的积温、出苗到拔节的积温、开花到灌浆的积温、潜在灌浆速率、光周期和最大穗粒数; (2) 交叉验证时, APSIM-Maize模型各参数变异系数在1.06%～23.32%之间波动, 总体上模型参数变异性小, 可靠性高; (3) APSIM-Maize模型经过参数率定后的模拟产量与实测产量具有较好的一致性(2= 0.72, RMSE = 401.5 kg hm–2), 模型在十大孔兑地区春玉米产量的评估中表现出较好的适应性。本研究为在农田试验数据有限情况下提高模型率定参数的可靠性提供了新的研究思路和科学依据。

APSIM-Maize模型; 交叉验证; 春玉米

近年来, 基于过程的作物系统模型被广泛应用于预测作物产量、评估环境变化对作物生长的影响、优化作物管理模式和指导育种及生产等方面, APSIM (Agricultural Production Systems Simulator)是其中较具代表性的作物模型[1]。在实践应用中, 由于APSIM模型参数众多, 且多数参数无法直接测定, 为了优化模型参数以提高模型模拟能力, 通常通过率定的方式获取参数值, 即调整模型参数,尽可能减少模型输出变量(如生物量、作物产量、物候期等)与观测数据的误差[2-3]。然而, 由于农田试验时间周期长, 观测数据的时间序列较短, 可用于参数率定的观测数据有限, 同时由于模型存在异参同效的影响, 即多组不同的参数具有相同或相似的模拟精度[4], 导致模型参数可靠性差, 从而增加模型模拟结果的不确定性[5]。异参同效问题在基于过程的物理模型中是难以避免的, 但可以通过增加观测数据数量和减少率定参数的个数来缓解, 从而提高模型参数的可靠性[6]。

在观测数据有限的情况下, 无法绝对地增加观测数据数量, 但可以通过提高有限数据重复利用率的方式增加用于参数率定的观测样本空间。交叉验证是提高有限数据重复利用率的有效方法, 该方法将大样本分为小样本分别进行率定和验证的方法[7], 可分为Holdout验证法、k-折交叉验证法和留一交叉验证法, 其中留一交叉验证法可有效用于有限数据的模型评估[8]。Mkhabela等[9]采用该方法检验回归模型的稳定性及模型预测产量的能力; Chipanshi等[8]采用该方法评估ICCYF模型对春小麦、菜籽油及裸地在3个空间尺度的模拟能力; Qian等[10]采用该方法率定多元线性回归模型参数, 以提高模型对春小麦的预测精度; Nurulhuda等[11]采用该方法对ORYZA (v3)模型参数的变异性进行评估。与其他方法相比, 留一交叉验证法可以消除随机划分建模样本集和验证样本集带来的偶然误差, 确保验证过程可被完全重复, 适合数据样本量较小的情况[12-13]。目前, 交叉验证虽然已用于部分作物模型参数变异性的评估, 但在APSIM-Maize模型参数变异性的评估中应用较少。本研究采用留一交叉验证法对APSIM-Maize模型进行交叉验证, 评估其参数在率定过程中的稳定性, 从而得到可靠的参数组合。

基于以上研究背景, 本研究的目的是: 采用留一交叉验证法评估APSIM-Maize模型参数的变异性, 并率定APSIM-Maize模型参数, 以实现在观测数据有限的条件下, 获得可靠的模型参数组合, 从而提高模型模拟能力。

1 材料与方法

1.1 研究区概况

本研究选取研究区为内蒙古十大孔兑地区(N39°47′40″— 40°33′30″, E108°48′35″—110°56′40″), 十大孔兑所在的行政区包括鄂尔多斯市达拉特旗全部, 准格尔旗、杭锦旗、东胜区的小部分地区, 面积共10,800 km2, 其中沙漠面积为2762 km2。该区域属于典型大陆性气候, 平均海拔高度约1000 m。该地区的土壤类型分布特征具有极强的地带性, 以栗钙土和风沙土为主。十大孔兑是典型的半干旱区, 年平均降雨在200～400 mm, 降水由东向西递减, 且降水主要集中在7月至9月, 在此期间的降水量占全年降水量71.2%。十大孔兑地区的平均气温7℃左右, 年蒸发量约2200 mm。该地区的粮食作物以春玉米为主, 主要分布在北部区域, 生育期为5月至9月。

1.2 APSIM模型输入数据

APSIM (Agricultural Production System Simulator)是澳大利亚农业生产系统研究组研发的农业生产系统模型, 目前被广泛应用于作物生长过程、作物产量、土壤水分平衡、溶质迁移、土壤侵蚀、土壤有机物及氮平衡等物理过程模拟[14-15]。APSIM模型的输入数据有气象数据、土壤数据、农田管理数据。本研究使用的气象数据来源于中国气象局气象数据共享服务网(http://www.nmic.cn/), 主要包括日尺度的降水量(mm)、最高气温(˚C)、最低气温(˚C)及日照时数(h)。日太阳辐射(MJ m–2)根据日照时数计算所得, 本研究选择了距离采样点最近的气象站, 以该气象站的气象数据作为输入数据。土壤数据来源于国家地球系统科学数据中心黄土高原分中心(http://loess.geodata.cn/ data/dataresource.html), 主要包括土壤容重、pH值、土壤黏粒含量及土壤沙粒含量。田间持水量根据土壤黏粒和沙粒含量百分比计算所得[16-17], 土壤饱和含水量根据土壤孔隙度计算。农田管理数据来源于达拉特旗农牧技术推广中心田间试验记录数据, 时间跨度为2012年至2019年, 其中2012年至2019年春玉米播种时间在5月1日, 收获时间在9月25日左右, 灌水量为450～540 mm, 灌水时间为5月1日至9月10日, 种肥施加量为210 kg hm–2, 追肥量为600 kg hm–2, 分别在拔节期、喇叭口期和抽雄期进行施肥, 各年份玉米产量及种植密度见表1。

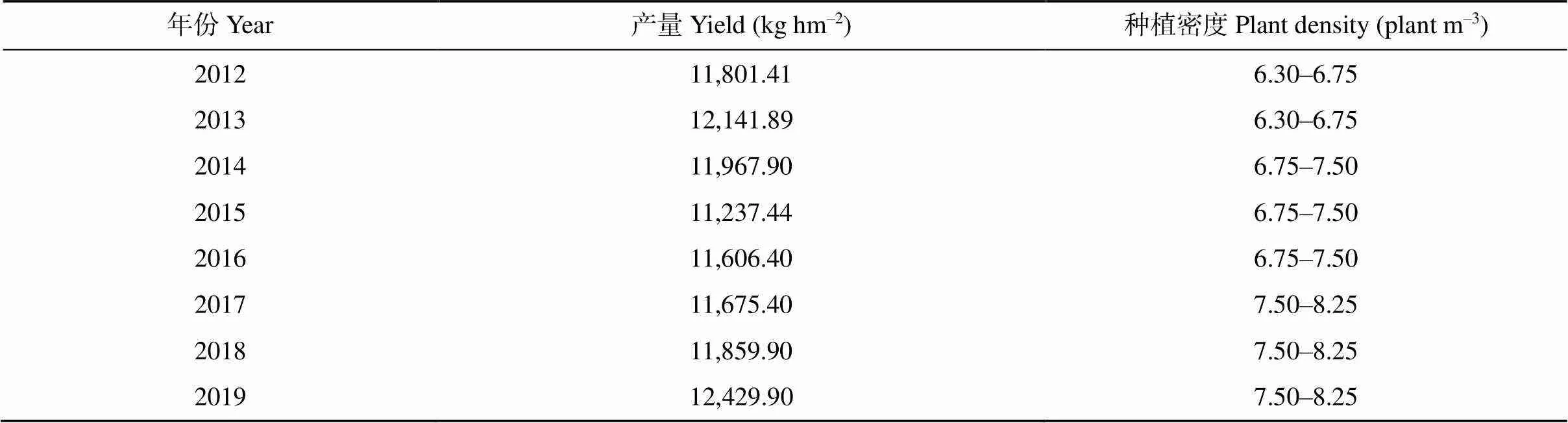
表1 2012–2019年春玉米产量及田间管理数据

1.3 敏感性分析方法

本研究运用扩展傅里叶幅度检验法(extended Fourier amplitude sensitivity test, EFAST)量化APSIM-Maize模型模拟产量对参数的敏感性。EFAST方法是Saltelli等[18]基于方差分解原理、综合了Sobol方法和FAST方法提出的敏感性分析方法。该方法采用一阶敏感性指数和全局敏感性指数评价参数敏感性高低。其中, 一阶敏感性指数评价单个参数对模型输出结果的直接影响, 全局敏感性指数评价参数之间的交互作用对模型输出结果的影响, 算法的详细介绍参考Saltelli等文献[15,18-19]。本研究利用R语言sensitivity包及apsimx包分别计算APSIM-Maize模型在2012—2019年的参数敏感性。首先根据https://www. apsim.info及相关研究[4,20-22]采用的参数选择需要调试的APSIM-Maize模型参数, 包括出苗到拔节的积温(tt_emerg_to_endjuv)、光周期(photoperiod_slope)、开花到灌浆的积温(tt_flower_to_start_grain)、开花到成熟的积温(tt_flower_to_maturity)、最大穗粒数(head_grain_no_max)、潜在灌浆速率(grain_gth_rate)、辐射利用效率(rue)和蒸腾效率系数(transp_eff_cf); 利用sensitivity包生成参数样本, 调用apsimx包更改APSIM-Maize模型参数并运行, 最后利用sensitivity包计算模拟结果的敏感性。每次敏感性计算运行×次, 其中为采样个数,为参数个数, EFAST方法中认为当参数采样个数≥65倍的参数个数(采样个数≥65×参数个数)时, 参数样本为有效[15]。基于各年份的参数敏感性分析结果, 根据全局敏感性指数的大小对参数进行排序, 并采用TDCC (top-down coefficient of concordance)系数衡量各年份参数敏感性排序的一致性, TDCC的计算方法参考Iman和Confalonieri等[23-24]的研究。最终计算2012—2019年各参数全局敏感性指数的平均值, 以此作为衡量模型参数敏感性强弱的依据。

1.4 APSIM模型交叉验证与率定

交叉验证是指将大样本分为小样本分别进行率定和验证的方法[7], 其目的是为了得到更可靠的模型或参数, 可分为Holdout验证法、k-折交叉验证法和留一交叉验证法。其中留一交叉验证法是指将原样本中的一项作为验证集, 其余的用于参数率定, 循环估计直至每个样本都被当作一次验证集(图1)。本研究采用留一交叉验证法评估APSIM-Maize模型参数的稳定性。以2012年的产量观测数据作为验证集, 2013—2019年的产量观测数据作为训练集, 根据参数敏感性强弱逐个调整参数。每次调参时, 利用R语言生成正态分布的参数样本并调用APSIM模型, 得到相应的产量模拟值, 认为RMSE最小时的参数为该参数样本中的最优值, 以最优值固定该参数, 按照上述步骤逐个调整其他参数, 该过程迭代进行, 直至RMSE最小,本次调参过程结束, 得到满足要求的参数集。然后将2013年的产量观测数据作为验证集, 将其他年份的产量观测数据作为训练集, 按照上述步骤率定APSIM模型, 以此类推, 直至所有年份均参与验证。该过程共率定APSIM模型8次, 得到8组参数集。考虑到各年份的气候条件、管理措施存在差异, 在评价交叉验证结果时, 计算8次交叉验证中各年份率定期的均方根误差(RMSE_Cal)和验证期的均方根误差(RMSE_Val)。根据交叉验证所得的8组参数, 计算变异系数(CV), 评估模型参数的稳定性。在参数变异性较小的情况下, 将2012—2019年所有年份的产量观测数据用于率定APSIM模型参数。

图1 留一交叉验证法示意图

RMSE和2分别表示第次交叉验证时的均方根误差和决定系数(= 1, 2, …, 8); RMSE_Cal和RMSE_Val分别表示第年在交叉验证率定期和验证期的均方根误差(= 2012, 2013, …, 2019)。

RMSEand2represent root mean square error and the determination coefficient at theth cross validation (= 1, 2, …, 8), respectively. RMSE_Caland RMSE_Valrepresent theth year’s root mean square of calibration and validation at cross validation (= 2012, 2013, …, 2019), respectively.

1.5 模型评估指标

本研究分别按照公式(1)、公式(2)计算决定系数(2)和均方根误差(RMSE), 对APSIM-Maize模型在十大孔兑地区的适应性进行评估; 按照公式(3)计算变异系数CV, 对APSIM-Maize模型的参数变异性进行评估。

2 结果与分析

2.1 参数敏感性分析结果

在2012—2019年逐年日尺度气象数据驱动下, 本研究对APSIM-Maize模型参数进行全局敏感性分析, 根据各参数在2012—2019年全局敏感性指数的平均值, 确定各参数的敏感性强弱, 其结果如图2所示。影响春玉米产量的参数敏感性由强到弱依次是: 蒸腾效率系数(transp_ eff_cf)、辐射利用效率(rue)、开花到成熟的积温(tt_flower_ to_maturity)出苗到拔节的积温(tt_emerg_to_endjuv)、开花到灌浆的积温(tt_flower_to_start_grain)、潜在灌浆速率(grain_gth_rate)、光周期斜率(photoperiod_slope)和最大穗粒数(head_grain_no_max)。

2.2 APSIM-Maize交叉验证及率定结果

依据APSIM-Maize模型的参数敏感性强弱对APSIM-Maize模型进行交叉验证及率定, 其结果如图3所示。图3-a表示APSIM-Maize模型在2012—2019年交叉验证和率定时的均方根误差(RMSE), 图3-b1～b8依次表示APSIM-Maize模型在8次交叉验证时模拟产量与实测产量的拟合情况, 图3-b9表示APSIM-Maize模型率定时模拟产量与实测产量的拟合情况。图3-a结果表明, 各年份的模拟误差存在差异, 导致APSIM-Maize模型模拟误差存在年际差异的原因有2方面: 一是模型结构限制; 二是气象条件存在年际差异。对比交叉验证时率定期与验证期的RMSE发现, 率定期的均方根误差(RMSE)均低于验证期的均方根误差(RMSE), 且8次交叉验证的决定系数2均≥0.7 (图3-b1～b8), 说明交叉验证结果拟合度较好, 且率定的参数较优。对比交叉验证与率定时的RMSE发现, 除2014年与2019年外, 其他年份率定时的RMSE均小于交叉验证时的RMSE, 说明采用留一交叉验证法在一定程度上可以减少由模型结构和气象差异所造成的误差, 该结果同时也说明增加用于参数率定的实测数据可以减少模拟误差, 这也反映出留一交叉验证法的优势。

图2 基于全局敏感性指数的参数敏感性排序

transp_eff_cf: 蒸腾效率系数; rue: 辐射利用效率; tt_flower_to_ maturity: 开花到成熟的积温; tt_emerg_to_endjuv: 出苗到拔节的积温; tt_flower_to_start_grain: 开花到灌浆的积温; grain_gth_ rate: 潜在灌浆速率; photoperiod_slope: 光周期; head_grain_no_ max: 最大穗粒数。

transp_eff_cf: transpiration efficiency coefficient; rue: radiation use efficiency; tt_flower_to_maturity: thermal time from flower to maturity; tt_emerg_to_endjuv: thermal time from emergence to end of juvenile phase; tt_flower_to_start_grain: thermal time from flowering to start grain-filling; grain_gth_rate: potential grain growth rate; photoperiod_slope: photoperiod slope; head_grain_no_ max: potential grains per head.

根据参数敏感性的强弱依次进行交叉验证, 所得的8组参数如表2所示。其中, 开花到成熟的积温(tt_flower_ to_maturity)的变异系数最低, 低至1.06%, 其次是辐射利用效率(rue) 2.42%、蒸腾效率系数(transp_eff_cf) 3.53%、出苗到拔节的积温(tt_emerg_to_endjuv) 5.07%、开花到灌浆的积温(tt_flower_to_start_grain) 15.39%、光周期斜率(photoperiod_slope) 18.24%和潜在灌浆速率(grain_gth_ rate) 23.32%。各参数在交叉验证时的变异性较小, 说明APSIM-Maize模型率定参数的稳定性较高。在此前提下, 利用2012—2019年产量数据对APSIM-Maize模型的参数进行率定, 确定最终参数值, 结果如表2所示。基于率定后参数开展APSIM-Maize模型模拟, 如图3-b9所示, 结果表明春玉米产量模拟值和实测值具有较好的一致性,2为0.72, RMSE为401.5 kg hm–2。这说明经过参数率定后的APSIM-Maize模型在十大孔兑地区具有较好的适用性, 能较准确模拟春玉米的年产量。

2.3 参数变异性的影响因素

分析影响参数变异系数存在差异的因素发现, 参数的敏感性强弱导致参数的变异性存在差异, 结果如图4所示, 图中横坐标表示参数的敏感性顺序, 数值越大表示参数的敏感性越弱。在总体趋势上, 参数变异系数随着参数敏感性的减弱而增加。这主要是因为敏感性强的参数对玉米产量影响较大, 小幅度的变动会导致玉米产量发生较大的变化, 而敏感性弱的参数对玉米产量的影响较小, 大幅度的变动可能对玉米产量的影响较小, 因此, 在模拟产量与实测产量的2达到0.70且RMSE较小的情况下, 敏感性弱的参数的变异系数较大, 而敏感性强的参数的变异系数更小。

图3 APSIM-Maize模型交叉验证与率定结果

(a): 交叉验证与率定时均方根误差比较, 其中RMSE_Cal表示交叉验证时率定期的均方根误差, RMSE_Val表示交叉验证时验证期的均方根误差, RMSE表示率定时的均方根误差; (b): 交叉验证(b1～b8)与率定(b9)时产量模拟值与实测值比较。

(a): the comparison of the root mean squared error (RMSE) between cross validation and calibration, among them, RMSE_Cal is the RMSE of calibration at cross validation, RMSE_Val is the RMSE of validation at cross validation, and RMSE is the RMSE at calibration. (b): the comparison of simulated and observed yield at cross validation (b1–b8) and calibration (b9).

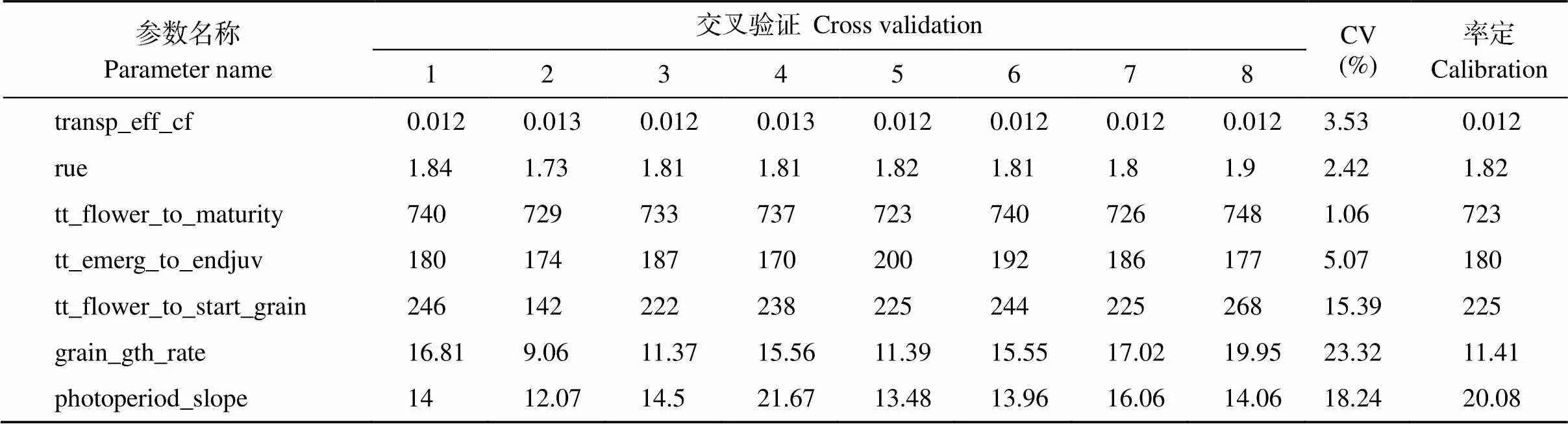
表2 交叉验证及率定参数集

参数名称的全称同图2。Abbreviations of the parameters are the same as those given in Fig. 2.

图4 参数变异系数与敏感性顺序的关系

3 讨论

本研究采用留一交叉验证法对APSIM-Maize模型率定过程中的参数变异性进行评估。在交叉验证的过程中, 率定期的均方根误差(RMSE)均小于验证期的均方根误差(RMSE), 说明交叉验证所得的参数较优, 在此情景下计算的各参数的变异系数更能真实地评价参数的变异性。交叉验证结果表明, APSIM-Maize模型参数变异系数在1.06%～23.32%之间波动, 均小于25%, 说明即使采用不同的输入数据对参数进行率定, 参数的变异性依然很小, 故可以采用所有年份的观测数据率定参数, 从而增加用于率定参数的观测数据的数量, 减少异参同效的可能性。本研究还发现, 参数的敏感性强弱导致参数变异性存在差异, 越敏感的参数, 其变异性越小, 这就意味着即使部分参数的变异系数相对较大, 但这些参数对APSIM- Maize模型模拟产量的影响较小, 对模型最终的模拟效果影响较小。

交叉验证可分为Hold-Out法、k-折交叉验证法和留一交叉验证法。目前, APSIM模型在参数验证时, 使用较多的是Hold-Out法, 即将数据集进行一次切分, 一部分用来训练模型, 另一部分用来验证, 该过程只进行一次。例如, Ahmed等[25]用2008年观测数据率定APSIM-Wheat模型参数, 用2009—2010年观测数据进行验证; Kheir等[26]用2019年的观测数据率定APSIM-Wheat模型, 用2020年观测数据进行验证; Wang等[27]用1996—2005年的观测数据率定APSIM-Maize模型, 用2006—2012年的观测数据进行验证。Hold-Out法通常只对数据集进行一次随机切分, 该过程增加了参数率定过程中的随机误差, 另外, 即使模型的模拟精度满足要求, 但用于参数率定的观测样本数量较小会增加异参同效的可能性[6]。k-折交叉验证需要把训练集分成k个子集, 将每个子集作为验证集, 该方法适合大样本的数据集[28]。留一交叉验证法不受训练集和验证集划分的影响, 可以消除随机划分数据集带来的偶然误差, 每一个样本都单独做过验证集, 几乎用到了所有样本信息, 适用于训练数据有限的情况[12-13]。本研究采用留一交叉验证法, 将有限的观测数据划分为8组不完全相同的数据用于APSIM-Maize模型参数率定, 并对率定过程中参数的变异性进行评估, 在APSIM-Maize模型参数变异性较小的情况下, 采用所有年份观测数据率定APSIM-Maize模型, 最大程度增加了用于参数率定的观测数据数量, 这不仅减少异参同效的可能性, 还有效降低模拟误差(图3-a)。

[1] Hao S, Ryu D, Western A, Perry E, Bogena H, Franssen H J H. Performance of a wheat yield prediction model and factors influencing the performance: a review and meta-analysis., 2021, 194: 103278.

[2] He D, Wang E, Wang J, Robertson M J. Data requirement for effective calibration of process-based crop models., 2017, 234/235: 136–148.

[3] Makowski D, Wallach D, Tremblay M. Using a Bayesian approach to parameter estimation; comparison of the GLUE and MCMC methods., 2002, 22: 191–203.

[4] Sheng M, Liu J, Zhu A X, Rossiter D G, Liu H, Liu Z, Zhu L. Comparison of GLUE and DREAM for the estimation of cultivar parameters in the APSIM-maize model., 2019, 278: 107659.

[5] Ramirez Villegas J, Koehler A K, Challinor A J. Assessing uncertainty and complexity in regional-scale crop model simulations., 2017, 88: 84–95.

[6] Her Y, Chaubey I. Impact of the numbers of observations and calibration parameters on equifinality, model performance, and output and parameter uncertainty., 2015, 29: 4220–4237.

[7] 李波, 孙翔龙, 姚名泽, 鲍慧, 王俊皓. 温室秸秆不同还田量条件下DSSAT-CROPGRO-Tomato模型的调参与验证. 生态学杂志, 2021, 40: 908–918.Li B, Sun X L, Yao M Z, Bao H, Wang J H. Parameter estimation and verification of the DSSAT-CROPGRO-Tomato model under the condition of different amounts of staw returned to the field in the greenhouse., 2021, 40: 908–918 (in Chinese with English abstract).

[8] Chipanshi A, Zhang Y, Kouadio L, Newlands N, Davidson A, Hill H, Warren R, Qian B, Daneshfar B, Bedard F, Reichert G. Evaluation of the Integrated Canadian Crop Yield Forecaster (ICCYF) model for in-season prediction of crop yield across the Canadian agricultural landscape., 2015, 206: 137–150.

[9] Mkhabela M S, Bullock P, Raj S, Wang S, Yang Y. Crop yield forecasting on the Canadian prairies using MODIS NDVI data., 2011, 151: 385–393.

[10] Qian B, De Jong R, Warren R, Chipanshi A, Hill H. Statistical spring wheat yield forecasting for the Canadian prairie provinces., 2009, 149: 1022–1031.

[11] Nurulhuda K, Muharam F M, Shahar N a N, Hashim M F C, Ismail M R, Keesman K J, Zulkafli Z. ORYZA (v3) rice crop growth modeling for MR269 under nitrogen treatments: assessment of cross-validation on parameter variability., 2022, 195: 106809.

[12] 赵子龙, 李波, 丰雪, 姚名泽, 解影, 邢经纬, 李长信. 温室环境不同灌水水平条件下DSSAT-CROPGRO-Tomato模型的调参与验证. 应用生态学报, 2018, 29: 2017–2027. Zhao Z L, Li B, Feng X, Yao M Z, Xie Y, Xing J W, Li C X. Parameter estimation and verification of DSSAT-CROPGRO- Tomato model under different irrigation levels in greenhouse., 2018, 29: 2017–2027 (in Chinese with English abstract).

[13] 陈召霞, 徐新刚, 徐良骥, 杨贵军, 邢会敏, 贺鹏. 基于新型植被指数的冬小麦覆盖度遥感估算. 麦类作物学报, 2016, 36: 939–944. Chen Z X, Xu X G, Xu L J, Yang G J, Xing H M, He P. Estimating vegetation coverage of winter wheat based on new vegetation index., 2016, 36: 939–944 (in Chinese with English abstract).

[14] Keating B A, Carberry P S, Hammer G L, Probert M E, Smith C J. An overview of APSIM, a model designed for farming systems simulation., 2003, 18: 267–288.

[15] He L, Zha G, Jin N, Zhuang W, Yu Q. Global sensitivity analysis of APSIM-Wheat parameters in different climate zones and yield levels., 2015, 31: 148–157.

[16] Saxton K E, Rawls W J, Romberger J S, Papendick R I. Estimating generalized soil-water characteristics from texture., 1986, 50: 1031–1036.

[17] 游松财, 邸苏闯, 袁晔. 黄土高原地区土壤田间持水量的计算. 自然资源学报, 2009, 24: 545–552.You S C, Di S C, Yuan Y. Calculation of filed capacity in the Loess Plateau region., 2009, 24: 545–552 (in Chinese with English abstract).

[18] Saltelli A, Tarantola S, Chan K P S. A quantitative model- independent method for global sensitivity analysis of model output., 1999, 41: 39–56.

[19] 宋明丹, 冯浩, 李正鹏, 高建恩. 基于Morris和EFAST的CERES-Wheat模型敏感性分析. 农业机械学报, 2014, 45(10): 124–131. Song M D, Feng H, Li Z P, Gao J E. Global sensitivity analyses of DSSAT-CERES-Wheat model using Morris and EFAST methods., 2014, 45(10): 124–131 (in Chinese with English abstract).

[20] Li J, Wang L, Luo Z, Wang E, Wang G, Zhou H, Li H, Xu S. Reducing N2O emissions while maintaining yield in a wheat-maize rotation system modelled by APSIM., 2021, 194: 103277.

[21] Ren X, Sun D, Wang Q. Modeling the effects of plant density on maize productivity and water balance in the Loess Plateau of China., 2016, 171: 40–48.

[22] Wang N, Wang E, Wang J, Zhang J, Zheng B, Huang Y, Tan M. Modelling maize phenology, biomass growth and yield under contrasting temperature conditions., 2018, 250–251: 319–329.

[23] Iman R L, Conover W J. A measure of top-down correlation., 1987, 29: 351–357.

[24] Confalonieri R, Bellocchi G, Tarantola S, Acutis M, Donatelli M, Genovese G. Sensitivity analysis of the rice model WARM in Europe: Exploring the effects of different locations, climates and methods of analysis on model sensitivity to crop parameters., 2010, 25: 479–488.

[25] Ahmed M, Akram M N, Asim M, Aslam M, Hassan F U, Higgins S, Stöckle C O, Hoogenboom G. Calibration and validation of APSIM-Wheat and CERES-Wheat for spring wheat under rainfed conditions: Models evaluation and application., 2016, 123: 384–401.

[26] Kheir A M S, Alkharabsheh H M, Seleiman M F, Al-Saif A M, Ammar K A, Attia A, Zoghdan M G, Shabana M M A, Aboelsoud H, Schillaci C. Calibration and validation of AQUACROP and APSIM models to optimize wheat yield and water saving in arid regions., 2021, 10: 1375.

[27] Wang Y, Lyu J, Wang Y, Sun H, Hannaford J, Su Z, Barker L J, Qu Y. Drought risk assessment of spring maize based on APSIM crop model in Liaoning province, China., 2020, 45: 101483.

[28] Levitan N, Gross B. Utilizing collocated crop growth model simulations to train agronomic satellite retrieval algorithms., 2018, 10: 1968.

Yield simulation from APSIM-Maize by using the leave-one-out cross validation approach

YANG Xue-Ning1,2, ZHANG Yong-Qiang1,*, ZHANG Xuan-Ze1, MA Ning1, and ZHANG Jun-Mei3

1Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;2Sino-Danish College, University of Chinese Academy of Sciences, Beijing 100101, China;3Dalat Banner Agricultural and Animal Husbandry Technology Extension Center, Dalat 014300, Inner Mongolia, China

The Agricultural Production Systems Simulator (APSIM) has been extensively used in crop yield estimation and agricultural management. Leave-one-out cross validation is a key way to improve the model simulation capability with the limited filed data. In this study, we evaluate the parameters sensitivity to maize yield and evaluate the reliability of parameters with the leave-one-out cross validation based on the sensitivity rank of parameters. These results showed that: (1) The sensitive parameters for maize yield were ranked in descending order as: transpiration efficiency coefficient, radiation use efficiency, thermal time from flower to maturity, thermal time from emergence to end of juvenile phase, thermal time from flowering to start grain-filling, potential grain growth rate, photoperiod slope, and potential grains per head. (2) The coefficients of variation of parameters fluctuated from 1.06% to 23.32%, which indicates that the variation of parameter was small and the reliability of parameters was high. (3) The adjusted APSIM-Maize model performed well in simulating spring maize yield (2= 0.72; RMSE = 401.5 kg hm–2), which indicates that the model had great adaptability in estimating spring maize yield in the Ten Kongduis. Our study provides an insight to improve the reliability of parameters with limited field data.

APSIM-Maize model; cross validation; spring maize

10.3724/SP.J.1006.2023.23064

本研究由“科技兴蒙”行动重点专项(十大孔兑综合治理与水资源集约高效利用集成示范) (KJXM-EEDS-2020005)和鄂尔多斯科技重大专项(鄂尔多斯陆地生态系统碳储量、碳汇核算及潜力评价) (2022EEDSKJZDZX016)资助。

This study was supported by the “Science for a Better Development of Inner Mongolia” Program (Integrated Demonstration of Comprehensive Management and Effective Utilization of Water Resources in the Ten Kongduis) (KJXM-EEDS-2020005) of the Bureau of Science and Technology of the Inner Mongolia Autonomous Region, and the Ordos Science & Technology Plan (Calculation and Evaluation of Carbon Storage and Carbon Sink in Terrestrial Ecosystem in Ordos) (2022EEDSKJZDZX016).

张永强, E-mail: zhangyq@igsnrr.ac.cn

E-mail: xnyang1999@163.com

2023-09-27;

2023-04-18;

2023-04-27.

URL: https://kns.cnki.net/kcms/detail/11.1809.S.20230427.1347.002.html

This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).