中国人口普查死亡数据质量评估及2010-2020年死亡模式转变分析

王金营，魏 晓

（河北大学 经济学院，河北 保定 071002）

一、引言

2020年全国第七次人口普查数据（下文简称“七普”）于2021年5月公布。纵观2000年以来进行的三次人口普查所显示的死亡数据，我国人口的死亡水平在过去20 年里发生了很大变化：一方面，人均预期寿命的延长较快。我国人口普查公报显示2000年人均预期寿命为71.40岁，2010年增长到74.83 岁。而由2020 年人口普查原始死亡数据计算得到的2020 年人均预期寿命则达到了81.75 岁（国家统计局公布的结果为77.93 岁）；另一方面，婴儿死亡率的下降速度很快，且相较于其他年龄段一直处于很低的水平。2000 年以来我国在生殖健康和孕产妇健康服务方面投入较大，服务逐步完善，特别是孕检、胎儿疾病干预、叶酸补充、医学必要的终止妊娠等，一定程度上提高了出生婴儿的健康程度和生存概率，这是值得肯定的巨大贡献。

同时我们注意到若直接用“七普”数据计算预期寿命，所得结果相当于最近10 年来我国人均预期寿命增长了6.92 岁之多。联合国步长法显示人均预期寿命在达到70 岁后每10 年增长2 岁，人类死亡数据库资料显示世界上最发达国家和地区也没有出现过在10年内预期寿命增长幅度远远超出这一水平的情况。我们也应注意到“七普”显示我国婴儿死亡率已经下降到1.4‰。婴儿死亡率与社会经济发展和医疗水平关系紧密，［1］而与大约同一时期（2019 年）的世界其他国家和地区相比（如美国婴儿死亡率是5.54‰，日本是1.86‰），我国婴儿死亡率甚至低于医疗水平更高、社会保障更全面的发达国家和地区；此外2020年我国卫生健康事业发展统计公报显示的婴儿死亡率为5.4‰，这与普查的结果也存在较大出入。根据国家统计局公布的信息，以往第三次至第六次全国人口普查（下文简称“三普”至“六普”）中总人口漏报率分别为0.26%、0.60%、1.81%和0.12%，这表明历次普查中均存在不同程度的人口漏报现象，同样死亡数据也存在漏报。从10年来预期寿命增幅过大、婴儿死亡概率超常表现和历次普查的经验三个方面判断，“七普”获得的婴儿死亡数据以及其他年龄段的死亡数据可能存在一定程度漏报。

2000 年以来我国社会经济发展水平、人民生活水平均有大幅度的提高，特别是覆盖城乡的医疗保障、养老保障等各项保障制度政策得到不断改革和完善，城乡居民健康水平得到大幅度提升，因而人口死亡模式发生了较为明显的变化。使用模型对“七普”死亡数据进行评估时需要充分考虑这一点。本研究将在布拉斯-罗吉特方法的基础上，针对不同年龄段死亡模式变化的特征对原有模型做出适应性调整，从而对“七普”死亡数据进行重新评估推算，并对死亡模式变动特征进行深入分析。

二、文献综述

人口普查的死亡数据质量评估是展开人口分析的基础。我国自1953年至今已经开展了七次人口普查。考虑我国人口基数庞大、地域广、差异大，如此大范围的普查工作不可避免地会存在调查数据偏误。自1982年第三次人口普查后，学界对普查数据质量的分析研究给予了充分关注。

（一）有关人口普查中死亡数据的漏报

已有文献显示1982 年进行的“三普”数据质量是相对可靠的，［2-3］是迄今为止数据质量最高的一次普查。即便如此，也有研究证明在低龄人口和死亡数据方面存在漏报，［3-5］只是程度较小。1990年进行的“四普”数据质量稍差，学界比较一致地认为死亡数据尤其是低龄组死亡数据明显存在漏报。张二力等人推断“四普”男性成人死亡登记的完整率为90%左右，女性成人死亡登记的完整率为85%左右。［6］婴儿死亡漏报问题突出，如翟振武的研究发现“四普”男性婴儿死亡率至少为44.7‰，女性婴儿死亡率为39.6‰，比未调整的分别高出15和5.9个千分点；［3］孙福滨等人测算1989年的分性别婴儿死亡率结果［7］印证了翟振武的结论。2000年的“五普”数据质量一直饱受争议，有研究认为“五普”死亡数据存在较严重的漏报问题，并大致判断其漏报水平在10.06%～15.00%之间；［8］黄荣清研究证明“五普”的65 岁以上人口存在死亡漏报。［9］与“五普”相比，2010 年“六普”0-4 岁婴幼儿和60 岁及以上老年人的死亡漏报都相当严重，王金营的研究显示男婴和女婴的死亡概率分别比普查值高出22.08‰和13.9‰；60-90 岁男性老年人的死亡漏报率超过20%，平均在23%左右，60-90 岁女性老年人的漏报率大多超过5%，平均在8%；［10］李成等人的研究结果是男女两性的婴儿漏报水平分别为77.3%和75.5%，老年人的死亡漏报水平分别为2.3%和7.0%。［11］由此看来，无论质量保障体系多么健全，公报显示的质量如何高，历次人口普查的死亡数据均存在漏报误差问题，这是统计规律和客观存在。

2020 年“七普”全面启用了信息化的调查方式，在技术上极大地提高了信息采集的精确度和效率。部分学者认为此次人口普查的漏报率实现了历史最低水平。［12］但是，调查方式的改进并不能完全解决死亡漏报等问题，数据质量依然受到普查员素质、区域经济发展和思想文化等因素的影响。尤其考虑“七普”数据所显示的婴儿死亡率与人均预期寿命等指标和当下社会经济发展水平并不相符，已有研究［1］［13］也显示“七普”与之前的历次人口普查一样存在一定程度的漏报问题，在运用这一数据进行测算预期寿命和分析死亡模式时，选取合适的方法重新评估“七普”死亡数据依然是有必要的。

（二）有关人口普查死亡数据评估和修正的方法

学界普遍认为造成死亡数据质量缺陷的主要原因有死亡漏报和年龄误报。［14］目前针对死亡数据质量评估的研究一般围绕死亡漏报这一问题展开。主流的几种方法有：

一是队列留存法。借助其他普查年得到的死亡数据进行年龄移算和比对来确定死亡漏报情况。如借助内插法，在“四普”人口年龄数据基础上对2000年普查时点人口年龄结构进行移算估计，然后将估计值与“五普”年龄结构数据进行比较分析，［15-16］从而找到人口漏报问题比较严重的年龄组；郭志刚认为各队列内部在出生和死亡上并非完全均匀分布，看到了内插分配的调整方法的不合理性，借助同年普查长表中抽样数据重新估计2000年年中人口年龄结构，以此来推计2000年与1990年两次普查间人口存活率，依然得到了“四普”低龄人口存在明显漏报的结论。［17］但这种方法一般建立在某次普查数据准确的假设上，仅作漏报的粗略估计。

二是拟合经验参数值法。如二维死亡（Logquad）模型、发展中国家死亡数据库（Developing Countries Mortality Database，简称DCMD）、模型生命表系统等。张震等人借助对数据质量较高的1982年普查数据进行修正之后得到中国分省模型生命表，重新拟合得到中国模式的二维死亡模型系数并讨论了其对中国人口死亡模式的适用性。［18］李成等人使用DCMD 生命表系统，结合联合国儿童基金会（United Nations International Children’s Emergency Fund，简称UNICEF）的儿童死亡率和华盛顿大学卫生计量与评估研究所（Institute for Health Metrics and Evaluation，简称IHME）的成人死亡率数据，对“六普”时期我国分性别的国民生命表进行重建并在此基础上估计了低龄组和老龄组死亡数据的漏报程度。［11］但DCMD 方法必须依赖相对准确的婴儿死亡率才能生成模型的关键参数，选择联合国调查数据并不能完全适应中国数据，中国人口普查获得的婴儿死亡率的准确性是无法保证的。同时，上述模型是大量国际实际死亡数据总结归纳而来，中国死亡模式与世界样本并不完全一致，直接应用难免会“水土不服”。

三是借助其他来源数据比对研究法。黄荣清等人利用模型生命表寻找婴儿和幼儿之间死亡率的关系，在此基础上借助各省（市）人均GDP 排名重新调整幼儿死亡率，进而实现对婴儿死亡率的修正。［19］此外，也有一些学者将目光投向户籍登记数据，借助户籍登记数据来考察历次普查人口数据质量。［4］［20-21］

四是模型生命表法。这类方法中最常见的是布拉斯-罗吉特（Brass-Logit）转换法。通过以中国高质量普查数据为依据建立模型，能更准确地反映中国死亡年龄分布情况，符合中国死亡率变化规律。同时，最大限度地利用了人口普查的原始数据，只需要保证观察年特定年龄段数据准确，即可高效实现其他年龄段死亡概率的修正。

（三）有关死亡模式变动分析

随着时间推移和社会发展，中国死亡模式发生了改变。李婷认为中国人口预期寿命的增长将逐渐转变为以内生因素提高为主的模式，这里的内生因素是指人类慢性衰老的过程。［22］从生命历程的角度来看，中国老年人衰老程度是随着年龄推移加速上升的。［23］杨磊等人通过构建虚弱指数解释老化速度，研究认为随着年龄的增长虚弱指数会加速提高，随之带来老年人老化速度的加快；虚弱指数越高，死亡风险也就越大。［24］在这样生物学规律的作用下，随着时间的推移，老年人群体的死亡概率变化应该呈现出先增速放缓，再加速增长的特点。当前社会经济以及医疗卫生事业快速进步发展，相邻两次人口普查间隔了10 年的时间跨度，期间的变化不容忽视。传统的二维死亡模型、DCMD 模型、布拉斯-罗吉特转换法等都无法准确描述这一变化。

然而，布拉斯-罗吉特转换法在对中国死亡数据的评估方面的优势仍是不可忽略的。笔者及其他学者在评估1990、2000、2010等年份的人口普查死亡数据时均采用了该方法。［7］［10］［25-26］由人口普查的死亡数据来看，1982-2010 年的近30 年间中国死亡模式的变化并不显著，因此以1982 年“三普”数据作为标准对“四普”“五普”的数据进行评估可以得到较为优质的效果。2000 年以来（尤其是2010年以来）经济发展和公共服务、社会保障、医疗保障等事业日新月异，死亡模式的改变十分明显，目前来看，继续使用以往的评估模型并不能很好地适应当前我国死亡模式。因此，本研究将在传统布拉斯-罗吉特转换法的模型基础上加以调整，使其更加适应中国当前死亡模式，并对2010年、2020年人口普查的死亡数据进行质量评估和重新推算。

三、布拉斯-罗吉特转换法的运用

（一）布拉斯-罗吉特转换法原理介绍

布拉斯-罗吉特模型的评估是要建立起标准生命表中年龄别死亡概率与评估年份的年龄别死亡概率之间罗吉特转换后的线性关系，从而借助标准生命表实现对其他年份死亡概率的评估和修正。

该方法的关键是确定被评估年份哪一年龄段的年龄别死亡概率与标准生命表对应年龄段死亡概率建立关联。2000 年及之前，由于受到传统习俗的影响以及出于对死亡避讳等各种心理，加之过去受妇幼医疗健康服务资源不足的限制，住院分娩比例不高，存在着婴儿死亡确认误差和缺乏主动上报婴儿死亡的意识，婴儿出生和婴儿死亡很难做到全面系统的登记。2010 年以来，随着公共医疗资源不断增多，居民健康卫生意识逐步提高，妇幼医院和病床等孕产妇助产服务资源明显增加，绝大多数人选择在医院分娩，相应地出生记录也更为全面，婴儿死亡数据的质量明显提高。当然，在部分医疗设施落后、交通闭塞的相对偏远的农村、山区，婴幼儿死亡漏报现象仍然存在。另外，1-5 岁儿童的死亡事件也不容易被家庭外的人们所注意，报告的及时性和准确性也存在问题。现实婴儿死亡率和低龄儿童死亡率可能远高于人口普查显示数值，存在漏报，需要被评估和修正。高龄组人口随着身体机能的下降和健康水平的降低，大大减少了社会参与和交往，有些老年人与周围社会的联系微弱，使其死亡漏报和延迟的可能性增加，另外也还存在故意瞒报的情况。因此，待评估年份的高龄组人口死亡数据也需要修正。

一般而言，介于少儿和老年人之间年龄段的群体多为在校学生或在岗就业人员，社会参与度较高，社会联系比较紧密，属于社会活跃人口，中间年龄段群体的死亡漏报可能性最小。因此，我们假设中间年龄组的死亡数据是准确的，不存在漏报（或者漏报率很低），可以选择待评估年份中间年龄段死亡概率与标准生命表相应年龄段死亡概率进行关联，建立罗吉特转换线性方程，回归估计模型参数，通过求解方程对低龄组和高龄组的死亡概率进行重新计算。

布拉斯-罗吉特转换法的基本公式为：

α表示待评估年份与作为标准年份的人口死亡率水平之间的差距；β代表死亡率年龄模式的差异。qx表示待评估年份死亡概率，代表标准年的死亡概率。选取恰当的、死亡数据准确的标准生命表是整个模型的关键。以高质量死亡数据为依据建立模型才能准确地反映死亡年龄分布情况，符合当前死亡率变化规律。

（二）标准生命表的选取及两阶段选择

已有研究证明1982 年人口普查是迄今为止最为成功的人口普查，［2-5］［13］人口年龄与性别分布均有较高的准确性和一致性，可以直接作为反映实际死亡水平的指标予以分析。因此，在使用布拉斯-罗吉特模型对中国死亡数据进行评估时，通常的做法是选取中国1982 年人口普查获得的死亡数据编制的生命表作为标准生命表。

当然，选取1982 年人口普查的死亡数据也存在一定的局限性。1982 年普查数据距离现今已接近40年。如前所述，40年来中国死亡模式已经发生了很大变化。随着时间的推移，观察年与1982年死亡模式的差距也在拉开。直接使用1982年年龄别死亡概率作为“标准”会使修正结果出现较大偏差。为了减少布拉斯-罗吉特转换法中选取的标准年份与观察年份时间跨度太大而加剧评估误差，将2010 年、2020 年的全国人口普查递次修正，即先以1982 年全国死亡数据作为标准对2010 年全国死亡数据进行修正，以得到的修正后2010年数据为标准再修正2020年全国死亡数据。

（三）针对年龄特点的模型适应性理论分析和调整方略

如前文所述，老年人群体的死亡概率增长变化是受到虚弱程度的影响。［24］［27］一般而言，在中高龄阶段，同一年龄的死亡概率是随着时间的推移而下降，同一年份的死亡概率是随着年龄的增加而上升的。随着生活水平、医疗水平的上升，社会保障越来越完备，中高龄段的死亡概率受时间效应而降低的幅度越来越显著，因此曲线上升趋势会越来越缓慢。然而，医疗等外部环境对于人类本身长寿改善的程度终究是存在极限的。在生命周期处于青壮年时期的死亡概率下降幅度很大，而由于更好的外部环境（医疗医学上的干预）而得以存活下来的人群，随着年龄的增长，在虚弱累积效应的作用下，当这部分人累积到更高的年龄阶段便发生更大的死亡风险，在高龄段出现相较以往更多的死亡事件，人口死亡概率上升更快。［22］呈现在年龄死亡概率曲线上的特点为中高龄段死亡曲线整体沿年龄轴（横轴）向右平移且更为平缓，高龄段死亡曲线陡升。

这样的变化趋势仅凭借使用1982年作为标准生命表、各年龄段以同一形式模型进行布拉斯-罗吉特回归是无法完美呈现的。因此，需要针对不同年龄段的特点对布拉斯-罗吉特模型进行适应性调整，使其符合当前年份的死亡模式。

在传统布拉斯-罗吉特方法的转换公式中，截距项α表示观察年与标准年人口死亡率水平之间的差距，体现的是时间效应对死亡概率的影响，即随着时间推移，同一年龄的死亡概率下降；系数β代表死亡率年龄模式的差异，反映的是同一时期（普查年）年龄之间内生效应对死亡概率的影响，即不同年龄之间的关联。［28］死亡概率在到达一定年龄之后便迅速上升，说明在高龄段时间效应对死亡概率下降的影响比较微弱。因此，在低龄和中高龄段，使用带截距项的布拉斯-罗吉特模型来拟合，在高龄段，由于1982年高龄段的死亡模式已不再适用当前年（2020年），这部分年龄的修正方程不带截距项。

结合前文中以2010年作为调整“过渡年”的思路，2020年的死亡概率具体修正流程如图1所示。

图1 调整后布拉斯-罗吉特转换法操作流程

四、具体计算过程

第一步，利用普查中年龄别平均人口、死亡人口等建立起原始数据生命表①具体公式参见曾毅等人编著的《人口分析方法与应用（第二版）》中生命表分析各部分。，包括年龄别死亡概率（qx）、当年平均存活时长（ax）、留存人数（lx）、留存人年数（Lx）、累计留存人年数（Tx）、人均预期寿命（ex）等信息。此时得到2020年男性人均预期寿命为79.24岁，女性为84.24岁。

第二步，将数据质量较高的1982 年中国人口普查分性别的死亡数据作为第一阶段死亡关联模型中的标准表，用来修正2010 年全国分性别的死亡数据。利用两次普查中死亡数据质量较为可靠的中间年龄组对方程系数进行拟合，建立起线性方程，通过求解方程对低龄组和高龄组死亡概率进行评估校正，得到男女两性的年龄别死亡概率。模型公式为：

qx表示死亡概率，α表示2010 年与作为标准生命表的1982 年人口死亡率水平之间的差距，反映时间效应对死亡概率的影响；β代表死亡率年龄模式的差异，反映年龄之间内部效应对死亡概率的影响。根据前面的分析，由于2010年死亡模式和1982年相比已经发生了较大转变，中高龄死亡概率上升趋势变缓，高龄死亡概率上升更迅速，说明在高龄段时间效应对死亡概率下降的作用很小，因此在高龄段进行拟合时，选择不带截距项α的公式，即：

第三步，将修正得到的2010年全国分性别死亡数据作为标准，建立其与2020年全国普查数据的关联模型，进行第二阶段的布拉斯-罗吉特转换，对2020年分性别死亡概率进行校正。公式为：

第四步，高龄组死亡模式还原。在布拉斯-罗吉特回归模型中，受关联生命表（也即1982 年和2010 年生命表）的影响，修正后的高龄组死亡概率数据并不是平滑的，死亡模式也会产生一定的变形。为解决这个问题，本研究将高龄以5 岁一组，将每5 岁漏报率取平均值，在原单岁死亡概率基础上借助漏报率重新修正死亡概率，公式如下：

为重新修正后死亡概率，qx为原始死亡概率，u为5 岁组平均漏报率。以此方法得到的高龄组死亡概率尽可能地保留了原始死亡模式形态，同时也保证了死亡概率曲线的平滑。

在修正得到的年龄别死亡概率基础上重新建立生命表，便可得到相应的人均预期寿命。

五、死亡数据评估与人均预期寿命测算

针对各年龄阶段人口社会活跃特点和死亡数据的特征，以10-60岁年龄段为可靠的高质量死亡概率数据与标准生命表相应年龄段死亡概率建立关联得到模型参数。具体过程是以1982年人口普查数据构建得到的生命表中死亡概率为标准，建立起布拉斯-罗吉特模型对2010年全国死亡数据进行修正，再以修正后的2010 年数据为标准完成对2020 年死亡数据的修正。参数的T值均通过了95%及以上的显著性水平检验，模型拟合优度均大于0.95，具体结果如表1所示。由此可知该模型的估计结果是可信的，可以用于对低龄组和高龄组的死亡概率的修正和评估。

表1 模型参数

（一）2020年人口普查漏报情况

1.低龄组漏报情况分析

将表1 所示的模型参数分别带入对应的公式（2）-公式（5）以及公式（6）可以得到修正后的2020 年分性别分年龄死亡概率。将修正得到的2020 年年龄别死亡概率与原始死亡概率做比对，可计算得到分年龄的死亡漏报率（见图2）。整体来看，男性低龄组漏报率要高于女性，其中男性0-9岁平均漏报率为75.33%，女性为57.69%。具体来看，男婴死亡漏报率为85.08%，女婴死亡漏报率为77.80%，3岁之前的男女两性漏报水平差距较小；3岁之后，女性随年龄增长漏报率下降幅度更大，趋势更明显。

图2 2020年人口普查0-9岁人口死亡漏报率

2.高龄组漏报情况分析

男女两性高龄漏报率在70-90 岁之间比较高，其中男性平均漏报率为22.55%，女性为20.75%；90 岁及以上的死亡漏报率比较低；老年阶段男性漏报率普遍高于女性。表2 展示了65-99 岁男女两性的具体漏报情况。

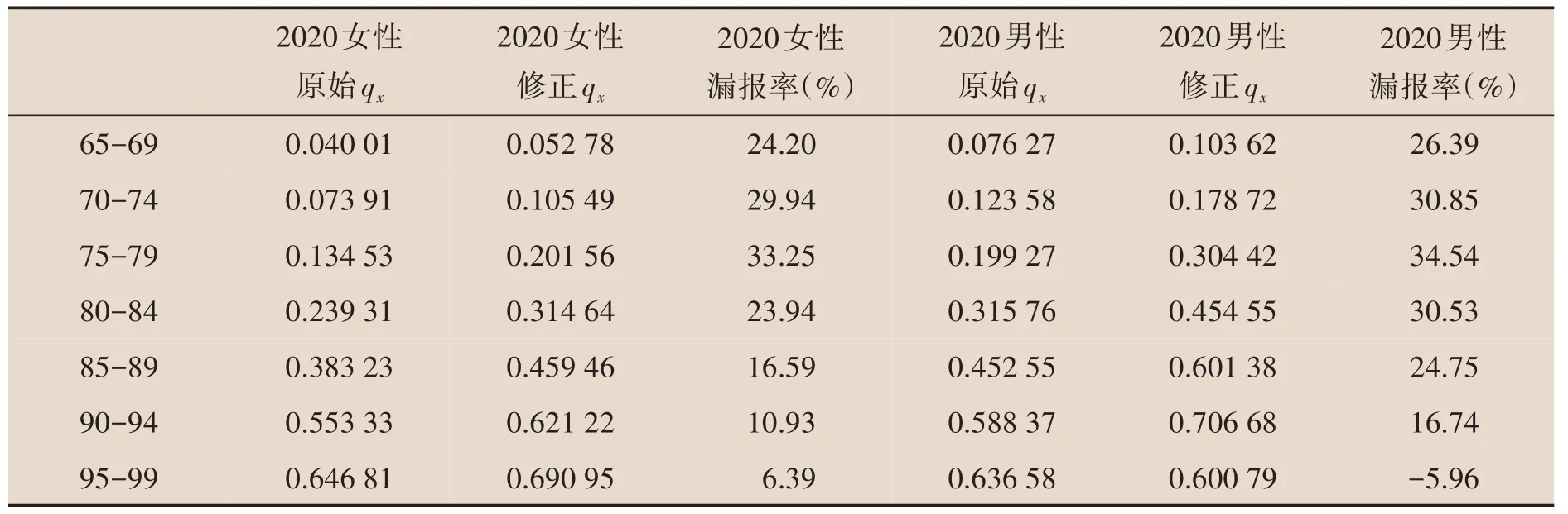
表2 2020年65-99岁男女两性死亡概率修正前后对比及漏报情况

本文评估的婴儿和高龄组的死亡漏报结果与李婷［1］通过多种方法评估的结果非常接近，表明“七普”婴幼儿死亡数据确实存在较大的漏报，也表明本文所采用的方法和模型具有可行性。

（二）2010-2020年死亡水平变化分析

1.婴幼儿死亡概率变动分析

从婴儿死亡概率来看，不分性别的婴儿死亡概率由2010 年的21.15‰下降为2020 年的8.80‰（见表3）。男婴死亡概率由22.10‰下降为11.14‰，10 年间降低了49.59%；女婴死亡概率由20.03‰下降为6.21‰，降低了69.00%。女婴死亡概率的下降速度大于男婴。从幼儿死亡概率来看，1-4 岁不分性别死亡概率由2010 年的9.08‰下降为2020 年的4.88‰，男性死亡概率由10.36‰下降为6.05‰，10年间降低了41.60%；1-4岁女性死亡概率由7.56‰下降为3.58‰，降低了52.65%。男女两性的幼儿死亡概率下降幅度均低于婴儿。

表3 2010-2020年婴幼儿死亡概率（‰）

值得注意的是2010年以来婴儿死亡概率的下降幅度较大。主要原因是2010年之后孕产妇健康服务水平等因素得到大幅度提高，这对婴儿死亡概率降低的效应远远大于其他年龄段，大大降低了婴儿死亡概率。由此可见采用模型修正得到的婴儿死亡概率可能略高于实际，即2020 年的实际婴儿死亡概率可能略低于8.80‰这一数值。国家统计局公布的2020 年婴儿死亡率为5.4%，这个数据可能也会比实际低。

2.2020 年年龄别死亡概率修正前后对比

将修正后得到的年龄别死亡概率与原始死亡概率对比（见图3），可以发现修正后的死亡概率曲线符合前期中高龄死亡概率增长减缓，高龄死亡概率上升加速的判断，且从修正前后高龄组死亡概率曲线的对比可知模型对于男性的死亡模式调整程度更大，高龄男性的漏报程度更高。

由图3 可知经过修正，男性死亡概率曲线在高龄段上升幅度更大，更为陡峭。而女性原始数据的死亡概率曲线与修正后死亡概率曲线的变化情况较为一致（见图4）。表明修正后保持了原有的年龄死亡概率曲线模式。女性的死亡模式与男性的死亡模式相比，曲线向右偏的倾向明显，尾部发生向下弯曲的年龄点相差5岁左右。

图4 2020年女性死亡概率修正前后对比

3.人均预期寿命变动分析由修正后得到的年龄别死亡概率构建生命表，可以进一步计算得到人均预期寿命值。

表4 中给出了2010-2020 年男女两性及合计的人均预期寿命和60 岁预期余命。2020 年不分性别人均预期寿命为78.21岁，比2010年的74.82岁增加了3.39岁，表明10年来我国人均预期寿命又有了较大提高，进一步证明这10 年我国社会经济发展和健康事业发展的成就斐然。2010 年女性人均预期寿命为77.40 岁，男性为72.18 岁，女性比男性高出5.22 岁；2020 年女性人均预期寿命突破了81岁，增长到81.20岁，男性增长到75.07岁，两者的差距已经增加至6.13岁，说明近10年来男性的人均预期寿命增长速度低于女性。从60 岁余命来看，我国老年人余命由2010 年的20.22 岁增长到2020年的21.56岁，增长了1.34岁。其中男性由18.46岁增长到19.29岁，增长0.83岁；女性由21.70岁增长到23.47 岁，增长1.77 岁，同样也是女性增幅更大。这说明随着时间的推移，我国男女两性间的人均预期寿命的差距仍在加大。

表4 2010-2020年人均预期寿命及60岁预期余命（岁）

六、2010-2020年死亡模式转变分析

（一）不同时期分年龄死亡概率比较

本文通过将相邻两次普查原始年龄别死亡概率作比值，观察1982-2020 年死亡模式的变化情况。

图5和图6显示了1982-2020年间我国男性和女性的死亡模式变化情况，从图5与图6比较可以看出在前20 年男性的死亡模式变化明显小于女性。2000 年之前，男性除低龄组外，其余大部分年龄组的死亡概率比值都接近于1，说明除低龄组外其余年龄组的死亡概率下降幅度不大，基本保持原有的死亡模式。但是在2000 年之后，低龄组死亡概率会出现大幅度的下降，中高龄组的下降也很明显，初步说明近20 年来男性死亡模式也发生了较大改变。

图5 1982-2020年男性年龄别死亡概率比较

图6 1982-2020年女性年龄别死亡概率比较

由图6 可知女性除高龄组外，其他年龄组的比值变化都比较明显，说明我国几十年来这部分年龄的女性死亡概率下降十分明显（尤其是低龄组），每过10 年，中低龄组死亡模式就已经发生了显著的改变；对于高龄组来说，1990 年、2000 年多数年龄组的死亡概率比值接近于1，说明1982-2000 年间高龄段的死亡模式变化不大，但2000 年后女性死亡模式变化十分明显。

（二）2010-2020年死亡概率曲线

根据上文对原始普查数据的分析，男女两性的死亡模式变化在2010 年显示出来非常大的变化。将1982 年、2010 年和2020 年死亡概率曲线放在同一图中进行比较，进一步观察死亡模式的变化情况（见图7 和图8）。

图7 全国男性1982年、2010年、2020年原始死亡概率曲线

图8 全国女性1982年、2010年、2020年原始死亡概率曲线

低龄组0-9 岁中，0-4 岁婴儿死亡概率下降趋势尤为明显。原始数据显示从1982年到2010年男女两性婴儿死亡概率分别下降了88.93%和87.67%，从2010 年到2020年分别下降了55.45%和64.80%。2010 年以来的10 年女性婴儿人口死亡概率下降幅度更大。

中间年龄组10-40 岁一直保持较低的死亡概率，变化幅度不大。

在40-95 岁中高年龄段，死亡模式整体呈躺倒的“L”形，随着时间的推移发生了明显的变化。

进入中高年龄段，不同年份的死亡概率曲线都开始逐渐爬升，但这一趋势出现的年龄逐渐后移。1982 年死亡概率曲线开始爬升的拐点发生在40～45 岁之间，2010 年这一拐点向后 推移了5 岁，2020 年在2010 年的基础上又向后推移了5 岁。具体可参见死亡概率曲线的斜率折线图（见图9）。

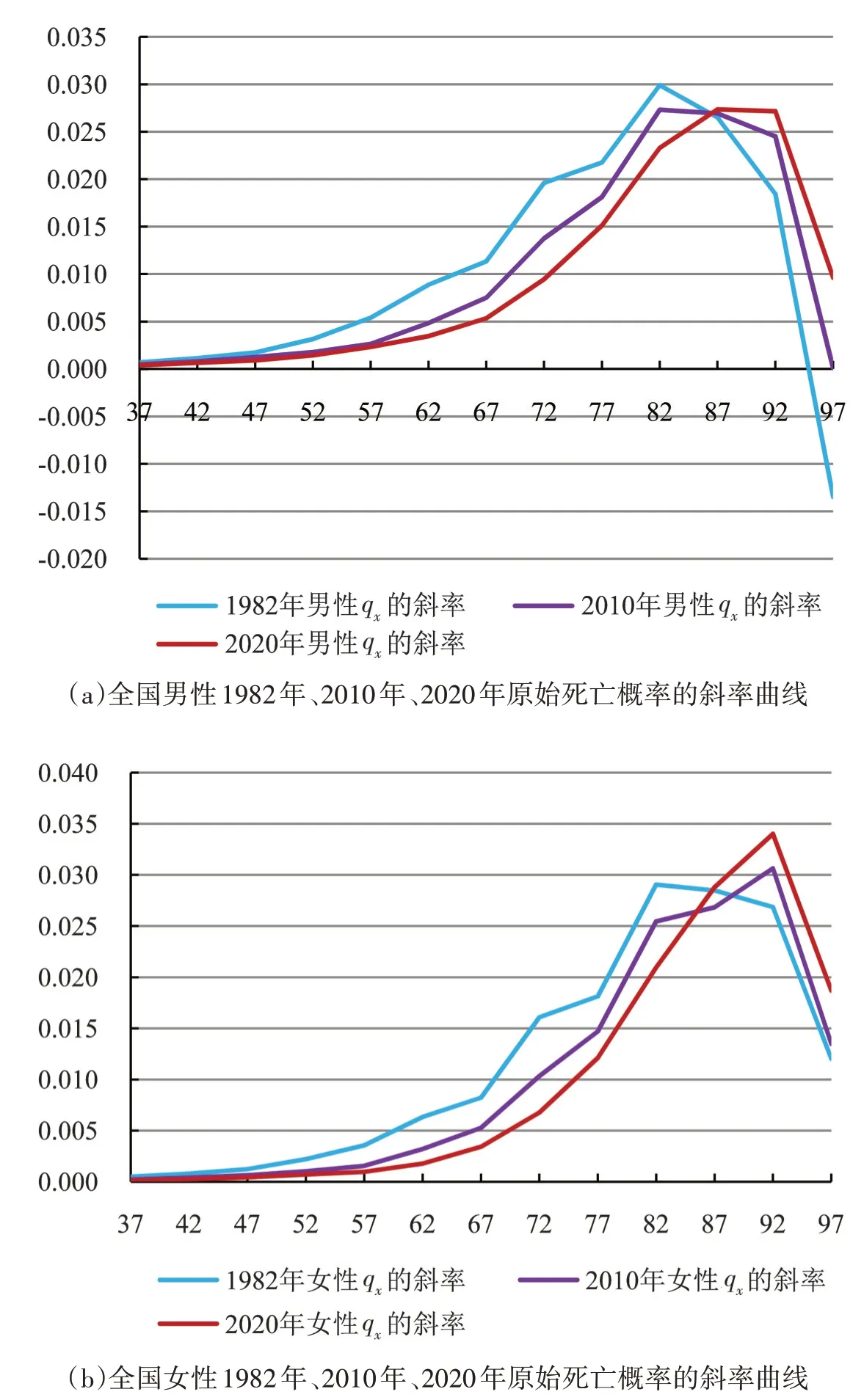
图9 全国原始死亡概率的斜率曲线

死亡概率随年龄增加变动的斜率曲线图反映的是死亡概率随着年龄的增加而增加的幅度。斜率的值越大说明死亡概率增长幅度越大，曲线越陡峭。从斜率的折线图可以直观看出随着年份推移，中高年龄组死亡概率曲线斜率的增幅越来越大。在图9 中任意画一条横线，与三条曲线的交点即是同一斜率出现的年龄点，2020年比2010年向后推迟5岁。

首先，1982 年时女性在47 岁开始死亡概率随着年龄的增大明显上升（斜率开始大于0.001），男性这一趋势开始的年龄稍早，出现在42 岁；到2010 年时女性死亡概率曲线这一拐点出现的年龄推迟至52岁，男性推迟至47 岁；2020 年时男女两性的死亡概率曲线出现明显上升趋势的拐点年龄又至少推迟了5 岁，女性在62岁之前出现，推迟10 岁，男性则在52岁之前出现，推迟5岁。

随着时间的推移，死亡概率曲线出现快速爬升趋势的年龄在逐渐向高年龄推移。

其次，中高年龄组的死亡概率曲线在爬升到一定程度后，会出现加速爬升的趋势，表现在曲线上就是陡度变大。从缓慢爬升到加速爬升，这一转折点出现的年龄也在逐年增加。曲线加速爬升的特点可以从斜率的增长率折线图中更为直观地看出（见图10）。

图10 全国原始死亡概率斜率的变化率曲线

斜率的增长率反映的是死亡概率曲线斜率变化值的变化情况，也即死亡概率增加的加速度。斜率的增长率值越大说明死亡概率增长速度越快，曲线爬升也就越快。从图10 可以直观看出在70 岁之前男女两性年龄别死亡概率曲线的斜率的增长率值均是逐年下降的，1982年死亡概率随年龄增大的加速度大于2010 年的加速度，2010 年的加速度又大于2020 年；70-80 岁之间是一个转换年龄段，在80 岁之后这一情况发生了逆转，2020 年年龄别死亡概率曲线的斜率的增长率大于2010 年，2010年又大于1982年。这说明在80岁之后死亡概率曲线随着时间推移呈现加速爬升。这一现象与虚弱累积理论相吻合。［22］［24］［27］即进入老龄前期人口死亡概率增长放缓同时也是一个虚弱累积的过程，虚弱累积达到一定年龄（70-80 岁）节点，老化速度就会加快虚弱累积的效应呈现，死亡更多被积压到更高的年龄段，带来更高年龄组死亡概率的加速增长。

同样地，在斜率的增长率折线图中画一条横线，可以看到70 岁前达到同样的死亡概率曲线的斜率增速所需要的年龄在逐年后移；而处于70-80 岁年龄段达到同样的死亡概率曲线的斜率增长率所需要的年龄逐渐提前。

最后，死亡概率曲线的加速上升会在到达一定年龄（80 岁左右）之后放缓；80 岁之后相同的斜率增长率随时间的推移所发生的年龄在提前，90岁之后差距逐步缩小。

图10 显示斜率的增长率值到达一定年龄后开始变为负值，1982 年女性发生在82 岁之后，男性稍早一些，在80岁之后；2010年女性发生在88 岁，男性发生在80 岁；2020 年女性也发生在88 岁，但能看出比2010年稍大，男性发生在88 岁。斜率的增长率值小于0 意味着死亡概率曲线开始减速上升。从这几次人口普查数据比较来看，随着时间推移，斜率的增长率的绝对值越来越小，体现在死亡概率曲线上就是曲线越来越平缓，且随年龄增加，这一平缓趋势越发明显。

95岁之后的变动特征无法借由死亡概率的斜率图呈现出来，但从原始死亡概率变动曲线可以看出。图7和图8显示95岁之后死亡概率曲线会出现一个峰值点，形状呈现一个“倒U”形。对比1982年、2010 年和2020 年的死亡概率曲线可以发现这一段“倒U”形曲线的峰值整体逐渐降低，且下降趋势变缓。

女性的这一峰值即最高死亡概率在1982年达到了281.94‰，发生在97岁；到1990年没有发生很大改变；2010 年于98 岁达到192.10‰的水平；2020 略有上升，在100 岁之前时达到189.78‰。1982年男性在94 岁时达到257.71‰，2010 年于97 岁时达到199.01‰，2020 年于98 岁时达到183.14‰。可见男性的死亡概率峰值普遍低于女性且近10 年女性死亡概率的峰值已经趋于稳定，未来继续下降的可能性不大，峰值年龄随着时间推移逐步向更高龄移动；而男性死亡概率峰值的下降幅度依然很大，未来可能存在继续下降的空间，达到峰值的年龄比女性略小，推迟的幅度较大。这同样表现出虚弱累积效应带来死亡风险达到峰值后，生存下来的高龄老年人虚弱指数较低、内生性健康水平较高，死亡概率反而降低。这一死亡模式的变动特征反映我国近20 年老年人健康水平有了较大幅度的提升。

从原始死亡概率曲线图中还可以观察到近年来“倒U”形的后半段的下降速度也变缓了，说明95岁之后，随着时间的推移，死亡概率随年龄增长而下降的幅度逐渐减小。

总体而言，我国死亡模式具有“低龄降低，中龄平稳，中高龄先缓升后陡升，高龄略有回降”的变化特点。同时，从两性差异来看，男性死亡概率曲线转折点的发生年龄一般稍早于同一时期的女性，且低、中龄死亡概率高于女性，男性高龄死亡概率则小于女性。修正后的死亡概率依然保持这个特点。男性死亡概率曲线更早发生转折就像是在死亡模式的时期发展上落后于女性，但是在生理等因素的影响下，前期男性死亡概率高于女性，这就使得相比于男性，女性会有更多死亡事件累积到了高龄，因此高龄组女性死亡概率反而高于男性。

2010 年死亡模式与1982 年相比，低龄组死亡水平已经下降很多，因此低龄组下降的空间并不大；中龄组无明显变化，始终保持低死亡水平，进入中高龄之后死亡概率上升趋势发生的年龄向高龄偏移了5岁左右，上升幅度也减小；上升加速的年龄同样向高龄偏移了5岁左右。

2020年修正前后的死亡模式有一定变化，尤其是男性，中高龄段死亡概率的上升趋势更加陡急。这是由于补齐了死亡漏报所致，同时也是前期死亡风险积累以及寿命极限发挥作用的结果。但是整体的死亡模式仍然呈现出相似的变化特点，且死亡概率曲线变化的拐点都在向后推移，其间伴随着因虚弱累积影响而导致的曲线斜率的变化。从死亡概率的最大值逐渐趋于稳定来看，我国死亡概率下降的空间在缩小，降低速度也在变缓；预期寿命正在向寿命极值靠近，未来的寿命增长不会再像过去的20多年那么快。

七、总结与讨论

本文利用布拉斯-罗吉特转换法，结合不同年龄段死亡模式的变化特点对模型本身进行适应性调整，最终实现对第七次人口普查死亡数据的评估检验，与李婷等所做研究结论有一个相互印证，也证明采用这一方法修正人口普查的死亡数据比较合适。最终结论表明“七普”所得死亡数据仍存在一定的漏报，漏报主要集中于婴幼儿和老年群体，且男性漏报明显大于女性。因而，在利用“七普”死亡数据进行人口分析时需要对漏报等质量问题进行评估。

近20 年我国婴幼儿和老年人的死亡概率有明显的下降，人均预期寿命也相应有明显提升。无论是婴儿死亡率的下降幅度还是人均预期寿命的增长幅度，相较于世界经验都要更大一些。前期我国死亡水平的下降和人均预期寿命的增长主要是温饱问题得以解决，而后期，由于我国医疗卫生、人民生活、社会环境等各个方面都实现了显著提升，实现了对居民全生命周期的健康保障，因此在综合考虑漏报因素之后仍会有高于世界一般模式的寿命增长速度。同时，本文通过年龄死亡模式变动分析，即年龄死亡概率曲线的斜率以及斜率的变化率分析，发现近20 年我国死亡模式已经发生了转变，反映了寿命延长极限的存在，并且在虚弱累积效应的作用下存在年龄上的死亡风险累积。随着寿命的延长和老龄化的发展，预计今后由虚弱累积带来的老年人失能规模也会越来越大，老年人口总死亡率和规模将持续增大。

本文所用修正方法已经尽可能还原当前中国的死亡模式，但准确度并非百分之百，修正得到的死亡概率也仅为估计值，不排除误差存在的可能性。